水下蒸汽渦輪發動機的動態建模與控制研究
吳亞軍,劉洋
(1.海軍裝備部,陜西 西安 710000;2.中國船舶集團有限公司第705研究所,陜西 西安 710075)
0 引言
無人水下航行器(Unmanned Underwater Vehicle,UUV)在捍衛國家安全、開發海洋資源等領域有著至關重要的作用,一直是各國的研究熱點。動力源作為其技術發展的主要瓶頸,直接影響水下航行器的性能[1]。受限于當前材料、設計和工藝水平等因素,傳統的水下航行器用活塞式發動機很難進一步提高功率。而現有電池的比能量又無法滿足水下航行器長時間續航的要求。以蒸汽渦輪發動機為主機的水下閉式循環系統具有高比能量、大比功率和無工質排放等優點[2],被視為高性能水下航行器動力源的未來發展方向之一。
采用蒸汽渦輪發動機作為無人水下航行器閉式熱力循環系統的主機,其經濟性也優于活塞式發動機[3]。如美國的MK50型魚雷即采用蒸汽渦輪發動機作為其Li/SF6閉式循環系統的主機,其最大航速超過50 kn,最大航深可達1000 m[4]。Li/SF6閉式循環系統如圖1所示。金屬Li和SF6在熱管反應器中發生反應,產生大量熱量。熱管反應器外壁被蒸發器包覆,其中的液態水吸熱變成蒸汽進入渦輪機,帶動渦輪機軸旋轉。做功后的乏汽經冷凝器冷卻后,變為液態水,由泵輸送進入下一個循環。
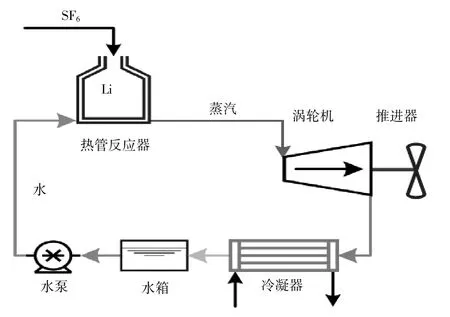
圖1 Li/SF6閉式循環系統
在實際工程中,轉速作為蒸汽渦輪機的控制目標,主要與進入發動機的蒸汽流量有關。渦輪機入口蒸汽流量可通過閉式循環系統中的水泵精準調控。隨著進入噴嘴的蒸汽流量增多,噴嘴室的壓力升高,進而流入汽缸的蒸汽流量增加,蒸汽渦輪發動機功率增大,轉軸轉速相應升高。因此,蒸汽渦輪機控制系統的控制量為入口蒸汽流量。在現有的研究中,渦輪機的轉速控制主要采用PID反饋控制[5-6],且各參數多為試湊法得出。利用試湊法求解PID參數,工作量大且易造成系統超調,嚴重影響系統性能。
針對以上問題,通過分析蒸汽渦輪發動機的動態過程明確了其關鍵動態環節,采用小偏差線性化的方法建立了其線性模型,在此基礎上進行PID控制,提出了一種基于遺傳算法的PID參數優化策略,并進行了仿真驗證。
1 渦輪機建模
建立蒸汽渦輪發動機的動態模型是設計控制系統的前提。然而蒸汽渦輪發動機中存在復雜的熱力、流體和機械效應耦合,因而其動態特性在本質上是非線性的。這些非線性特征將隨初始條件和當前工況的變化而變化,導致采用非線性模型設計的控制系統難以保證控制效果,因此在工程實踐中仍需建立線性模型,并用線性控制設計技術進行控制器設計[7]。
從動態角度分析可知,蒸汽渦輪發動機的工作過程中有兩個動態環節,一個是噴嘴,另一個是轉軸,因此可以將蒸汽渦輪發動機簡化為由蒸汽容積模塊和轉子模塊構成的物理模型,如圖2所示。

圖2 蒸汽渦輪發動機的簡化物理模型
1.1 蒸汽容積模塊
由氣體流動的連續性方程可知

由流量特性可知蒸汽容積的出口流量與其壓力成正比,即q2=kp,代入式(1)得
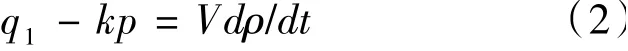
假設氣體的狀態變化是按多變過程進行的,即p/ρn=常數,則該式兩邊取對數并求導得:

將式(3)代入式(2)得

因為p,ρ均是時變的,所以式(4)本質上是非線性的。采用小偏差線性化的方法將其轉化在工作點附近轉化為線性方程。設p0,ρ0,q0均為額定工況下所對應的參數,則每一個變量都可以寫成額定值加變化量的形式,即p=p0+△p;ρ=ρ0+△ρ;q1=q10+△q,將以上各式代入式(4)得:
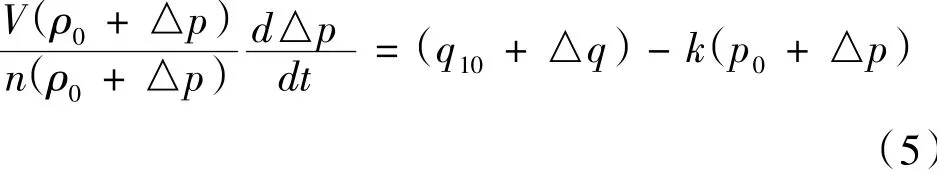
因為在額定工況下出入口流量均等于額定流量,即qm0=q10=q20,且q20=kq0,將以上兩式代入式(5)得

因為△p,△ρ與p0,ρ0相比是一個微小的變化量,因而可以將V(ρ0+△ρ)/n(p0+△p)近似為Vρ0/nqm0。實踐表明,這種小偏差線性化所帶來的誤差僅為1%~2%。所以式(6)可以簡化為
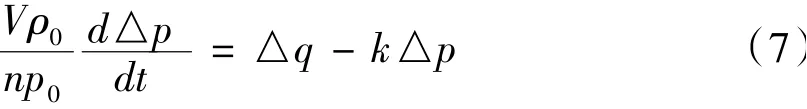
將式(7)兩邊同時除以額定流量qm0,得

上式中的各變量習慣上用額定值的百分比表示,即△q/qm0=xq,△p/p0=xp,則式(8)可寫成
將式(9)兩邊進行拉氏變換可得

式中,T0=Vρ0/nqm0稱為容積時間常數,用以描述容積慣性,即以額定流量qm0向蒸汽容積中注入體積為V的蒸汽時,使蒸汽容積中的蒸汽質量從零增加到D0=Vρ0所需要的時間。
1.2 轉子模塊
轉子的力矩平衡方程為:
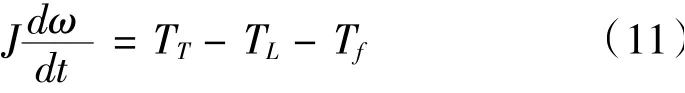
式中,J為轉子的轉動慣量,ω是轉子的角速度,TT是蒸汽轉矩,TL是負載的反轉矩,Tf是摩擦轉矩。
相應的轉子功率平衡方程為:
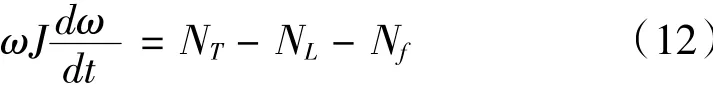
式中,Nf是一個與ω有關的非線性函數,NL是一個外部變量。
對式(12)進行小偏差線性化,可得
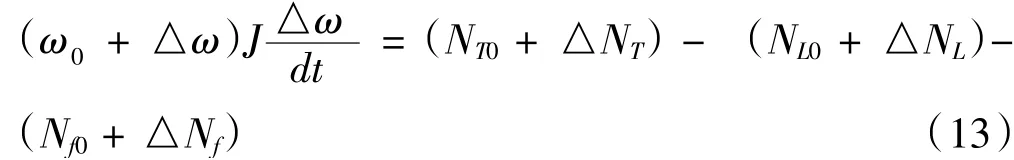
因為額定工況下NT0-NL0-Nf0=0,并將(ω0+△ω)J△ω/dt近似為ω0J△ω/dt,式(13)可化為

式(14)兩邊同時除以額定功率NT0,可得
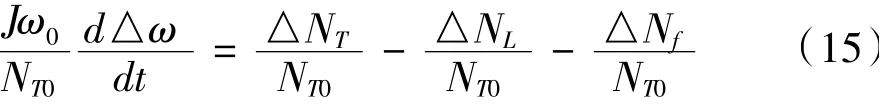
上式中的各變量用額定值的百分比表示,即△ω/ω0=xn,△NL/N0=xNL,△NT/N0=xP。此外在工作點附近△Nf可以表示為
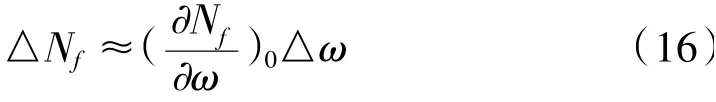
將以上各式代入式(15)可得

式(17)可以簡化為

將式(18)兩邊進行拉氏變換,得

式中,Tα稱為轉子飛升時間常數,用以描述轉動慣性,表示轉子在額定功率的蒸汽主力矩作用下,轉速由零飛升到額定轉速所需的時間。β稱為自平衡系數,與附加損耗有關。
最后,將蒸汽容積模塊和轉子模塊聯結起來,得到蒸汽渦輪發動機入口蒸汽流量與輸出轉速的關系框圖,如圖3所示。

圖3 蒸汽渦輪發動機的傳遞函數框圖
2 基于遺傳算法的PID參數優化
PID控制由于具有算法簡單、魯棒性好、可靠性高等優點而被廣泛應用于系統控制領域。其典型傳遞函數為:

PID控制器參數kp,ki,kd調整是否恰當,將直接決定此控制器的控制效果。PID參數整定一般采用手工試湊或優化的方式。前者工作量大且效果不理想。PID參數優化則通過數學方法對kp,ki,kd進行優選,從而使目標函數達到極值,因而本質上是一個參數尋優問題。采用優化方法整定PID參數工作量小,且精度高,控制效果好。因此,通過構造基于性能指標加權的目標函數,采用遺傳法對PID參數進行優化。
為獲得良好的動態特性并減小控制輸入的波動,PID參數優化的最小目標函數選為:
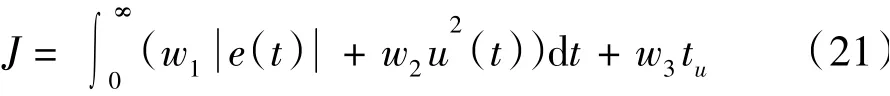
式中,e(t)為系統誤差,u(t)為控制器輸出,tu為上升時間,w1,w2,w3為權值。
此外,可添加超調懲罰項以避免超調,此時目標函數為
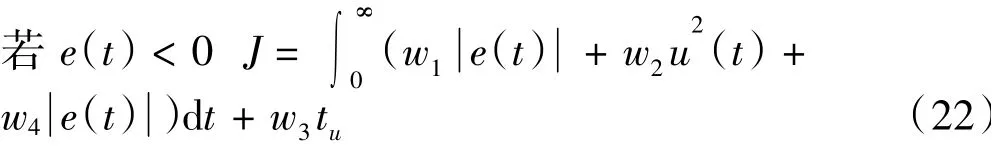
式中,w4為權值,且w4?w1。
遺傳算法是一種基于生物遺傳和進化機制的尋優搜索算法,因其具全局優化能力且收斂迅速,已廣泛應用于函數優化等方面。其基本思想是根據問題的目標函數構造一個適應度函數,對由多個解(每個解對應一個染色體)構成的種群進行適應度評估和遺傳運算(包括復制、交叉和變異),經多代繁殖后最終獲得適應度值最好的個體作為問題的最優解[8]。應用遺傳算法優化PID參數的基本流程如下:
(1)把每個PID參數按照一定編碼方案進行編碼得到字串,再將這些字串聯成一個完整的染色體,即個體;
(2)隨機產生由N個個體構成的初始種群;
(3)將種群中各個體解碼成對應的參數值,用此參數求目標函數值;
(4)計算適應度函數;
(5)應用復制、交叉和變異算子對種群中的個體進行操作,形成新一代的種群;
(6)反復執行步驟(3)~(5),直至滿足收斂判據為止,解碼后輸出PID參數值J。
優化流程圖如圖4所示。
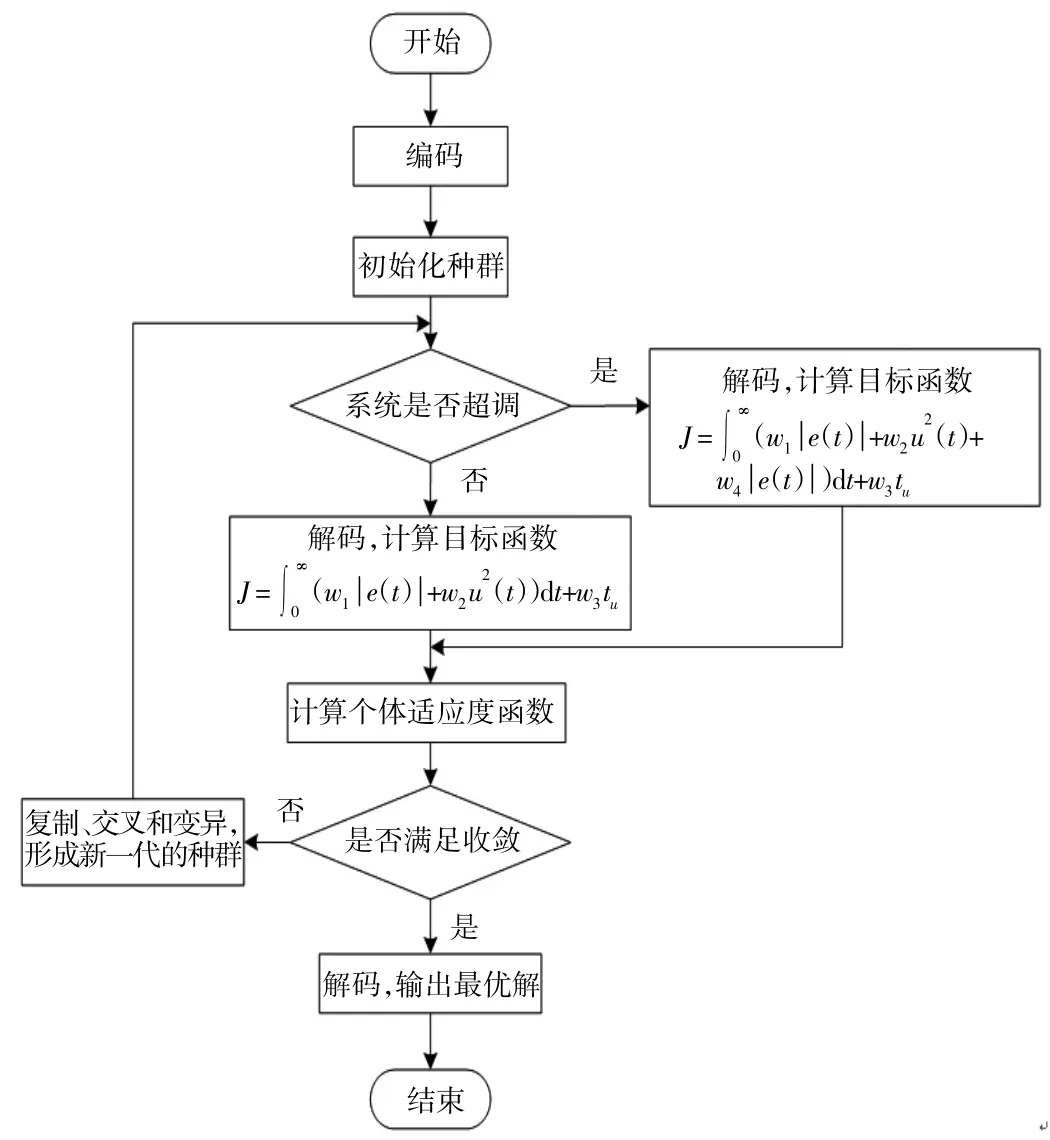
圖4 遺傳算法優化PID參數流程圖
3 仿真實驗
為驗證該PID參數優化方法,以所建立的蒸汽渦輪發動機模型為控制對象進行仿真研究。假設蒸汽渦輪發動機的負載為零,其他參數分別為:Tα=0.16,T0=1,β=0.83,則其傳遞函數為:
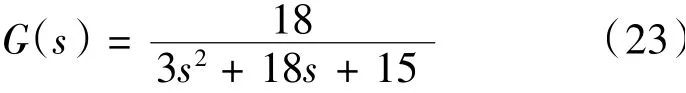
遺傳算法采用實數編碼方式,其參數選擇見表1。

表1 遺傳算法參數
經過100代進化,獲得的優化結果如下:kp=4.7929,ki=2.5064,kd=1.4187,性能指標J=99.6934。性能指標的優化過程如圖5所示。由圖可知,采用遺傳算法收斂至最小值實際只需約30步的迭代計算,證明該算法收斂速度快,優化效率高,是一種適用于工程應用的參數尋優方法。

圖5 性能指標J的變化曲線
采用整定后的PID控制系統階躍響應如圖6、圖7所示,其中圖6為轉速變化曲線,圖7為入口蒸汽流量變化曲線。圖中數據均做了無量綱化處理,它們是實際值與額定值的比值。可以看出,經過參數優化的PID控制器響應快速、無超調,控制效果良好。

圖6 小波包前面板

圖6 蒸汽渦輪發動機的轉速變化曲線

圖7 蒸汽渦輪發動機的入口蒸汽流量變化曲線
4 結語
通過分析蒸汽渦輪發動機的動態過程明確了其關鍵動態環節,采用小偏差線性化的方法建立了其線性模型,并在此基礎上進行PID控制,提出了一種基于遺傳算法的PID參數優化方法。仿真實驗證明遺傳算法收斂速度快,優化效率高,是一種適用于工程應用的參數尋優方法,經過參數優化后的PID控制器響應快速、無超調,控制效果良好。

