基于Adams和MATLAB的賽車轉向系統聯合仿真優化

劉仕康，周坤，樊昕宇

（燕山大學，河北 秦皇島 066000）

0 引言

大學生方程式賽車最早起源于上世紀的美國。中國大學生方程式汽車大賽（簡稱“中國FSC”）是一項由全國高校車輛工程或汽車相關學科在校學生組隊參加的賽車設計與制造比賽。2010年第一次舉辦大學生方程式比賽,參數隊伍近20隊，2022年增加到了近100隊。大賽車隊要求在一年時間內制造一輛符合賽事規則和制造標準小型單座方程式賽車并參加靜態答辯和動態測試形式，以總分高低決定勝負[2]。轉向系統關系到賽車的操縱穩定性，對整車性能起著重要的作用，通過對轉向系統的優化，有利于改善轉向操縱穩定性和輕便性。本研究提出了用Adams/insight模塊和Matlab聯合仿真的思想，對轉向阿克曼系數和輪跳時前束角的變化進行優化，使實際阿克曼系數曲線與理想阿克曼系數曲線擬合程度越好的同時，輪跳時前束角的變化也在可接受的范圍內。

1 FSEC轉向數學模型[3]

斷開式轉向梯形分為：梯形、轉向器前置，梯形前置、轉向器后置，梯形后置、轉向器前置，梯形后置、轉向器后置4種形式。受限于賽車內部狹小空間的布置，為了轉向時防止橫拉桿與制動、雙橫臂懸架、輪輞產生干涉。我們采用的是斷開式梯性前置、轉向器前置的布置方式，根據賽車內部實際的轉向結構，建立實際的內外輪轉角關系，如圖1所示。

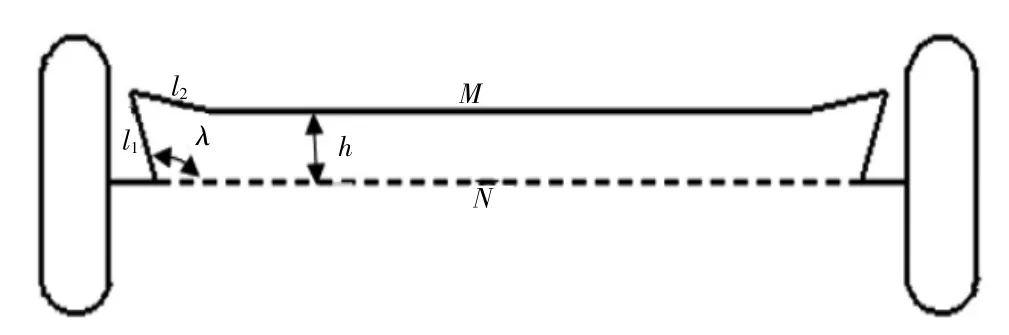
圖1 轉向梯性整體結構圖

為了清楚地表達動態轉向時的內外輪的轉角關系。繪制當車輪向左轉動時，左右車輪運動簡圖，如圖2所示。

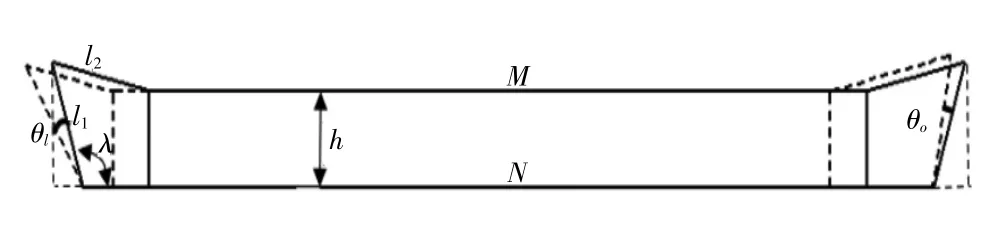
圖2 轉向輪實際轉角關系示意圖

車輪左轉，外輪轉向角度為θo，根據幾何關系可知：

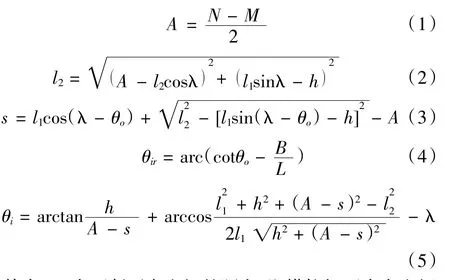
其中：M為兩斷開點之間的距離，即橫拉桿兩內點之間的距離，mm；N為兩側車輪主銷延長線在地面上交點之間的距離，mm；h為前置轉向器與前軸之間的距離，該距離用于定位轉向器位置，也是所謂的梯性高，mm；L為梯性臂的長度，mm；λ為梯性底角；A為計算算子；l2為拉桿長度，mm；s為齒條行程，mm；θi為內輪轉角；θir為符合標準阿克曼關系的內輪轉角；θo為實際外輪轉角。

從公式中可以看出，由梯性參數所構成的內外輪轉角極度非線性，且包含的優化變量眾多，使用常用的優化函數無法達到很好的優化結果，因此考慮利用Adams/insight工具來進行優化，并用Matlab檢驗的方式來實現聯合優化的效果。

2 Adams多目標優化

2.1 建立Adams轉向懸架模型

初步確定轉向幾何后，用Adams/Car建立轉向懸架虛擬樣機模型如圖3所示。進行平行輪跳仿真。為后面導入Adams/Insight模塊作準備。

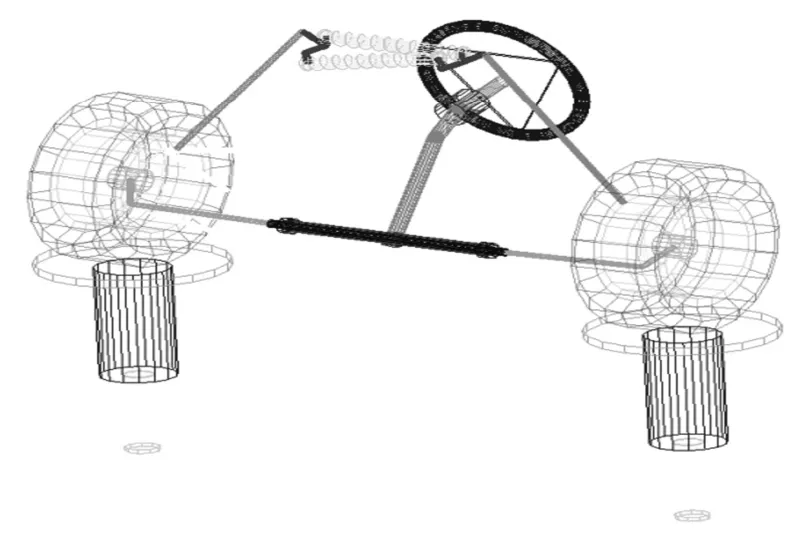
圖3 懸架轉向虛擬樣機模型

用Matlab編寫程序得到實際阿克曼系數（阿克曼系數就是考慮輪胎側偏時的內外輪轉角差與不考慮輪胎側偏時的內外輪轉角差的比值）和加入側偏角時阿克曼系數的差值。阿克曼系數的意義在于修正側偏情況下的內外輪轉角關系，如圖4、圖5所示。當得到較好的阿克曼系數狀態下的輪跳時束角的變化卻不是很理想，如果對阿克曼系數單一變量進行優化時得到的懸架轉向模型工況輪跳時前束角的變化就不是很理想。如果只對前束角進行優化，不考慮阿克曼系數的變化，則利用Adams/insight模塊對前束角優化，不斷迭代使前束角變化到最小，此時阿克曼系數就會變的不理想。因此能對輪跳時前束角的變化和阿克曼系數同時優化是最好的選擇。

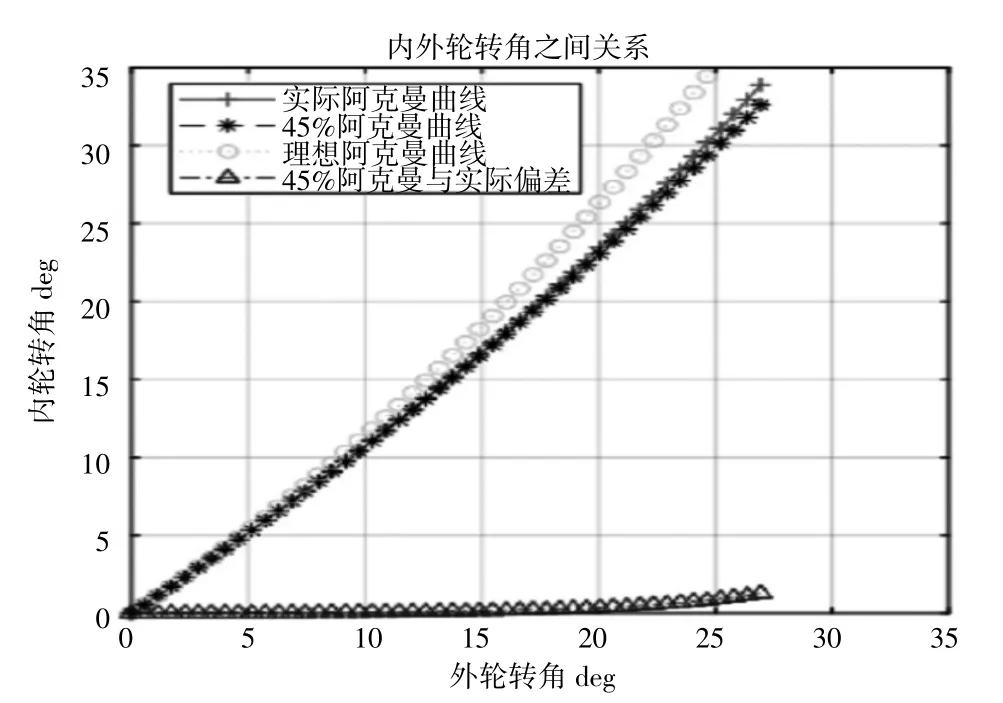
圖4 優化前阿克曼系數隨內外輪轉角變化圖

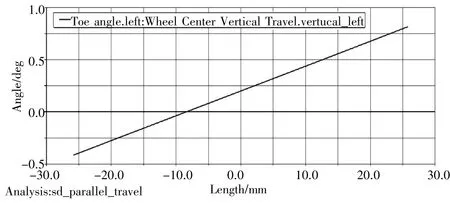
圖5 優化前前束角隨輪胎跳動變化圖

2.2 基于Adams/Insight模塊對阿克曼系數和前束角進行多目標優化

通過Adams/Insight模塊對轉向梯形進行多目標優化，可以同時優化阿克曼系數與前束角的變化，避免出現優化單一變量而另一個變量出現變差的情況。

（1）點擊Design objective命令尋找目標值，目標值選取為“仿真中的最大絕對值”。

（2）點擊adams/insight命令進入adams/insight模塊，找到要優化的點，調節其想要的運動范圍并命名。

（3）最后求解，等其運算結束后，顯示其結果，輸入實驗名稱進入結果頁面。

（4）根據自己預想的優化結果賦予兩個優化目標合適的比重（對于特定路況行駛的車輛，例如FSEC，轉向工況較多，應多考慮阿克曼系數，因為匹配的阿克曼轉向可以使得四輪盡可能地做純滾動從而減少輪胎的磨損，如果直線路況較多，應多考慮輪跳時前束角的變化，因為輪跳時前束角變化過大會影響車輛的直行穩定性，不足轉向和過度轉向，權重的值根據車輛的目標路況來確定，然后得到優化后的結果。考慮到我們有更多的轉向工況，這里選取阿克曼系數的權重為0.7、前束角的變化為0.3，如圖6所示。

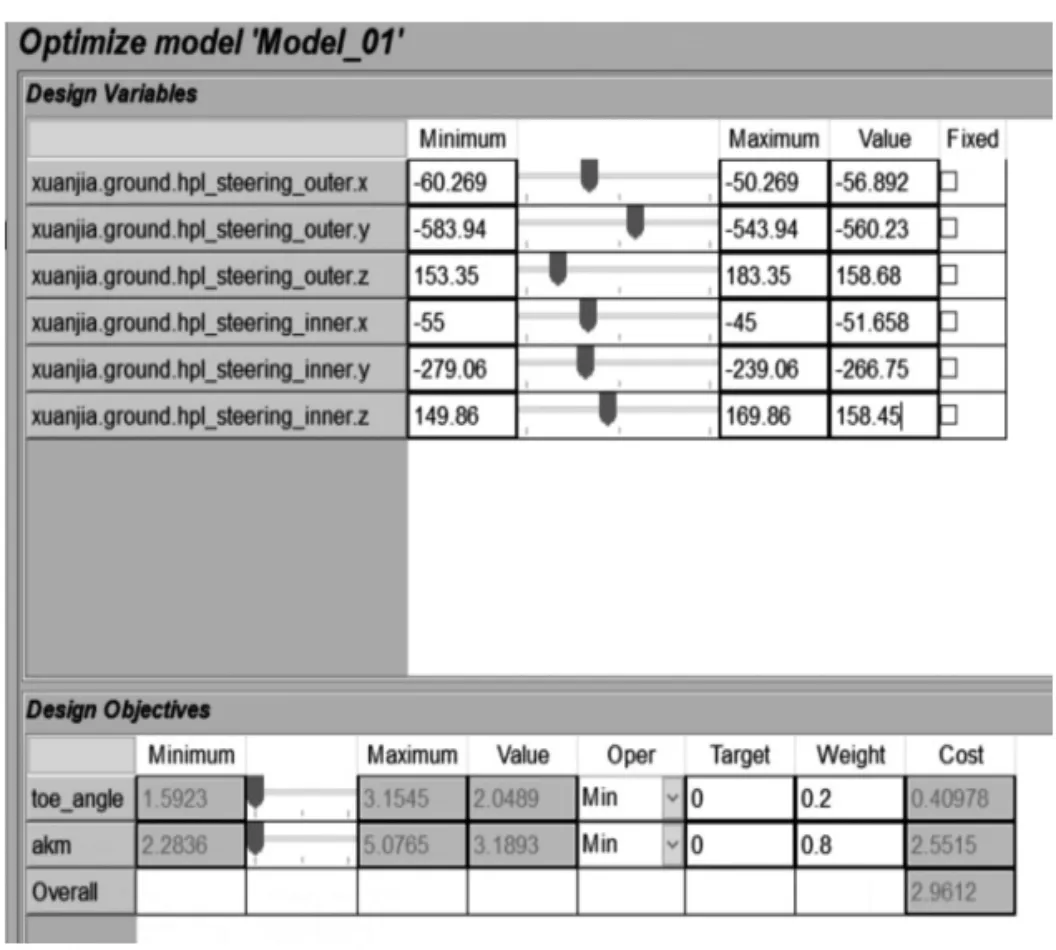
圖6 優化結果圖

（5）得到優化后的硬點坐標后，將其轉化為對應的梯性參數，見表1。由表1可知，梯形底角明顯變小，節臂長和梯形高沒有明顯變化，由此得出，轉向梯形中梯形底角對轉向性能有較大影響。

表1 梯形參數

3 Matlab對優化結果的驗證

3.1 標準阿克曼轉向關系[4]

轉向不考慮側偏角的影響，如圖7所示。為了讓賽車轉向時的各個車輪都只做純滾動運動，一方面可以提高賽車在過彎時的操縱穩定性能；另一方面可以減小因滑動而帶來的輪胎不均勻的磨損。此時，轉向中心應位于賽車后軸線的延長線上，此時內外輪轉角應符合標準阿克曼轉角關系：

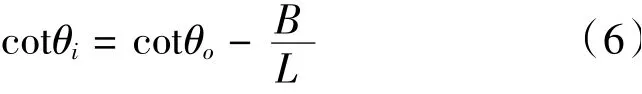
式中，θo為外輪轉角；θi為內輪轉角；B為主銷后傾角為0°時，兩側車輪主銷與地面交點之間的距離，mm；L為軸距，mm。

由（6）式得，在給定的外輪轉角下，內輪轉角為：

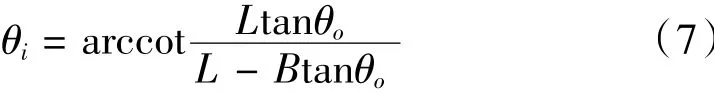
3.2 考慮側偏角時的左右輪轉角關系[3]

標準阿克曼轉向關系沒有考慮在實際工況下由于高速過彎時存在的側偏角，這會導致轉向中心并不位于后軸延長線，而是距后軸有一距離m，如圖7所示。

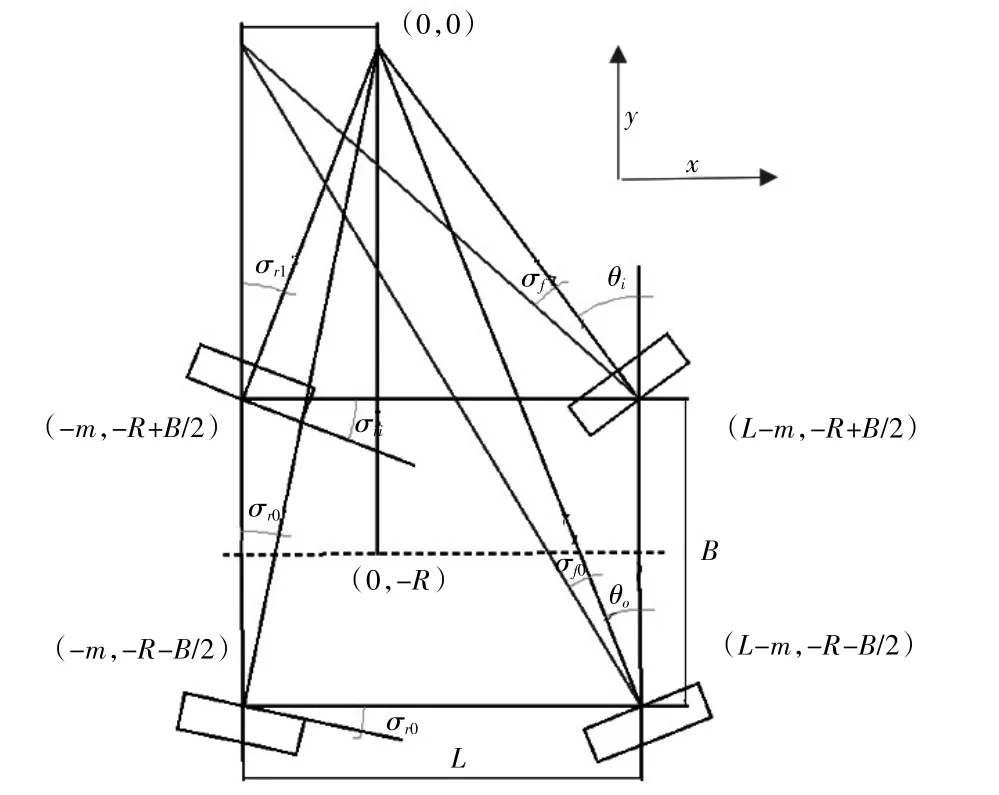
圖7 考慮側偏角時左右輪轉角關系

為了便于推導，在考慮側偏角時轉向左右輪關系式，以轉向中心為原點，汽車前進方向為X軸正方向，垂直X軸指向上方為Y軸正方向，建立坐標系。設轉彎半徑為R，轉向中心偏離后軸距離為m，軸距為L，輪距為B，則各點坐標如圖7所示。

根據三角函數關系，推出算式：

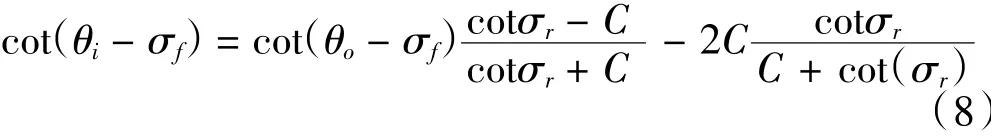
式中：θi為理想內輪轉角；θo為理想外輪轉角；σf為前軸中點側偏角；σr為后軸中點側偏角；C=B/2L。

式（8）即為考慮了側偏角對轉向輪影響的理想內外輪轉角關系式。如果給出輪胎側偏角，就能夠根據下文的式（11）計算出考慮輪胎側偏角時的內外輪轉角關系。

3.3 確定阿克曼系數

在前文中，通過設置阿克曼權重來決定硬點優化時阿克曼對硬點優化時的影響程度，而為了驗證硬點優化的合理性，則我們必須通過其他的手段來確定一個合理的阿克曼系數。

（1）定義阿克曼校正系數[4]

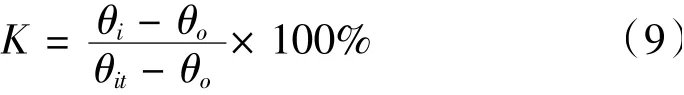
其中：θi為實際內輪轉角；θo為實際外輪轉角；θit為當外輪轉角θo為滿足標準阿克曼公式的內輪轉角。根據定義可知，當K=1時，即為標準阿克曼轉向；當K=0時，實際內外輪轉角相同，為平行轉向；當K＜0時，外輪轉角角度大于內輪轉角角度，為反阿克曼情況。阿克曼校正系數可以很好的描述轉向關系由標準阿克曼關系向平行轉向過度的程度。當定義了阿克曼校正系數之后，目標轉向關系的優化設計其實就是阿克曼校正系數的優化。

通過阿克曼校正系數可以定量化地描述轉向梯性的關系特性。因此，我們可以將目標轉向關系—即合理的內外輪轉角關系轉變成阿克曼校正系數的優化。

（2）建立目標轉向關系優化函數[4]

將（9）代入（7）中可得：

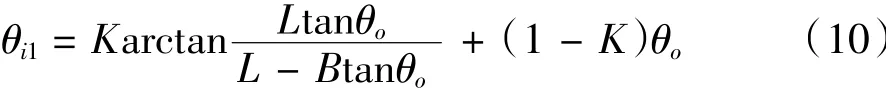
根據（8）可得

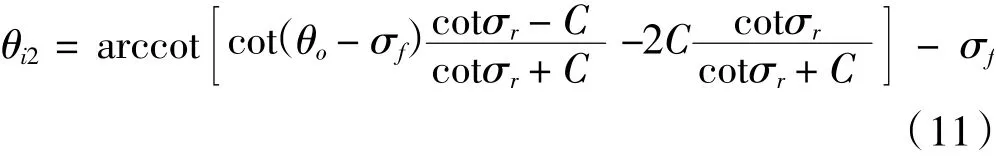
合理的目標轉向關系，即合理的阿克曼校正系數應該保證θi1與θi2盡可能地接近，兩曲線應盡可能吻合。

引入加權因子ω構成目標轉向關系優化函數如下

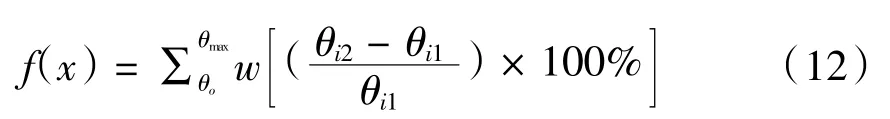
其中：w表示賽車行駛過程中方向盤各角度使用頻率。

方向盤上的轉角記錄儀器記錄了耐久賽過程方向盤轉角數據，通過對不同角度使用頻率進行分析可知，10°以下的轉角使用較為頻繁，10°～20°的轉角次之，20°以上轉角頻率最低，確定加權因子如下：w=1.5（0＜θo＜10°）

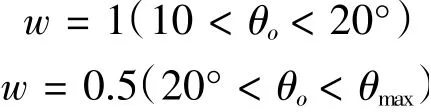
K值的優化范圍為0≤K≤1，根據最小轉彎半徑確定θmax=27.627°。

利用Matlab編寫優化程序，運行得到優化結果如圖8所示。從曲線圖中可以看出，隨著阿克曼校正系數的增大，誤差也就是理想和實際的車輪轉角差值出現先減小后增大的變化，當我們取誤差值最小時，也就是實際與理論差距最小，就得到了我們想要的阿克曼校正系數，為45%，此時實際與理想最小意味著轉彎時做純滾動的能力是在所有阿克曼校正系數中最強的，這正是我們想要的。

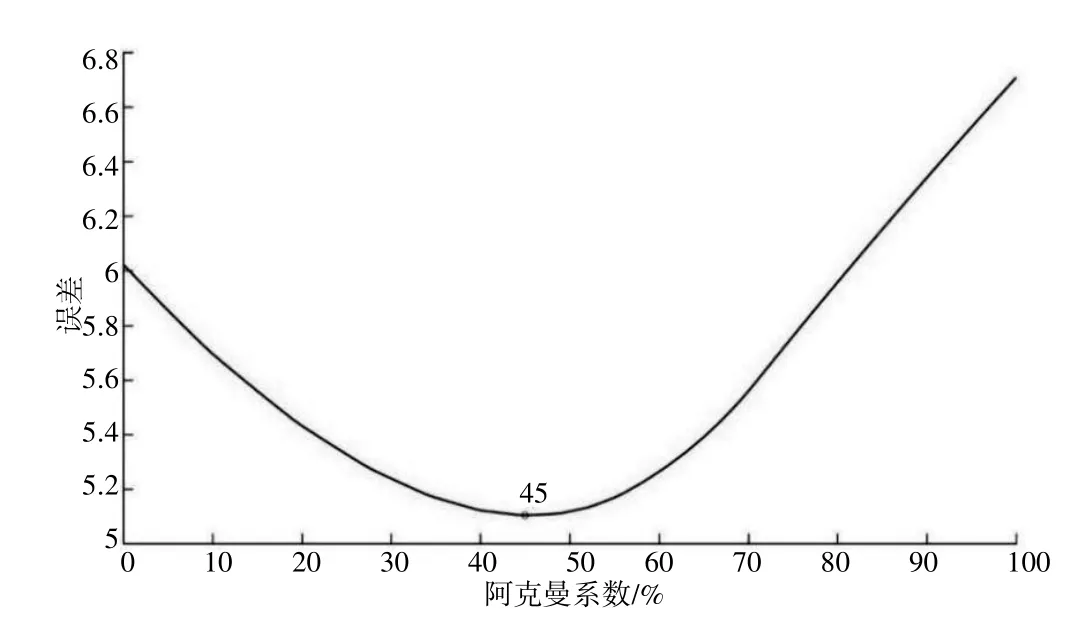
圖8 阿克曼優化曲線

在優化時要注意考慮輪胎側偏角對轉向關系的影響的基礎上，這里根據賽事的典型工況——“八”型繞環的極限工況下的載荷轉移來考察所賦予的合適的前后輪側偏角，最后得到最佳阿克曼校正系數為45%，并得到目標轉向關系為：

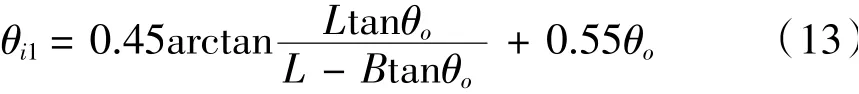
3.4 對優化結果驗證

通過前面推出的帶阿克曼校正系數的目標轉向關系和前文提到的實際機構的內外輪轉角關系，當兩者的曲線靠的足夠近，或者相對優化前有了較大的提升，就說明了優化的正確性。優化結果對比如圖9、圖10所示。

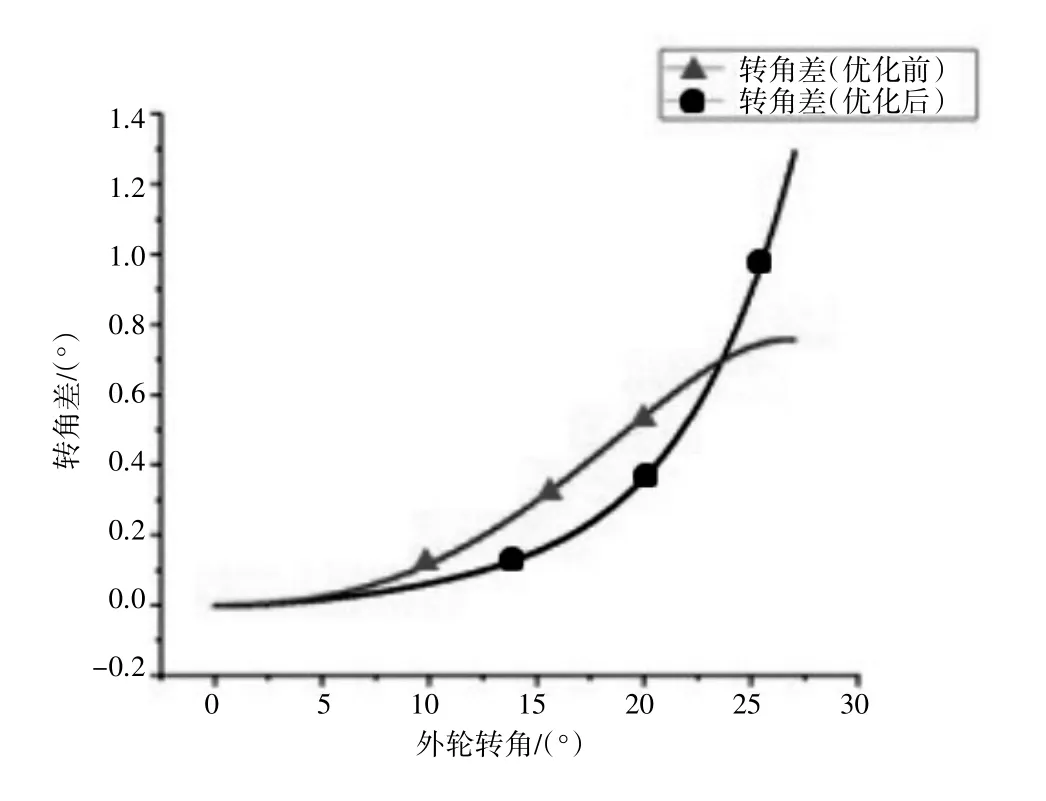
圖9 優化前后轉角差對比

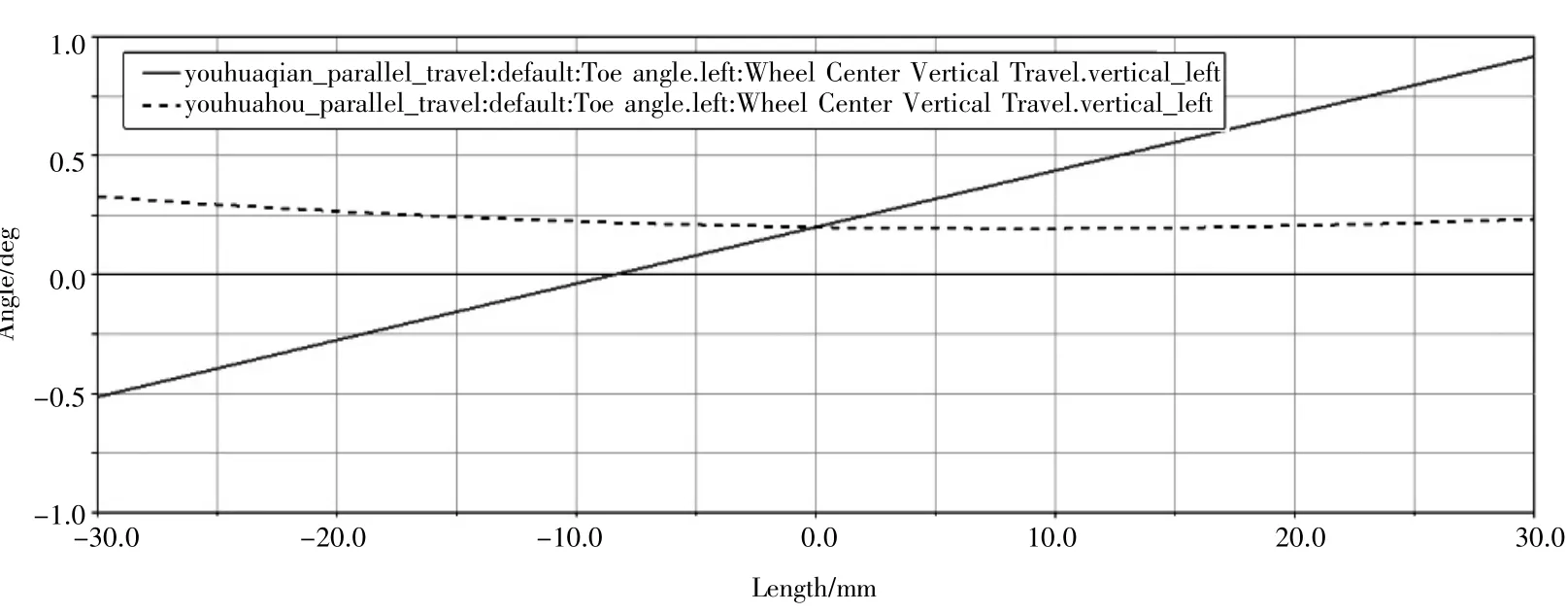
圖10 優化前后前束角隨輪胎跳動變化圖

結果表明，輪跳時前束角的變化明顯減少，使輪跳時前束角的變化由1.5°降低為0.25°，降低了83%，最大轉角差值由1.291°減小為0.7548°，降低了41.53%。優化效果顯著，證明了本方法的有效性。

4 結語

以中國大學生方程式為背景，提出了一種基于Adams/car insight模塊以輪跳時前束角的變化以及阿克曼系數為優化目標對轉向系統節臂點和斷開點的優化方法。詳細分析了轉向硬點的優化步驟，文中提及的優化方法相對于一般的優化方法更具簡便性和實用性，大大減少了設計周期，對FSEC轉向系統的優化具有一定的參考作用。