GNSS-A直線測量模式及航跡組合優化分析

馬越原， 楊元喜， 曾安敏

1 北京跟蹤與通信技術研究所， 北京 100094 2 信息工程大學， 鄭州 450001 3 地理信息工程國家重點實驗室， 西安 710054 4 西安測繪研究所， 西安 710054

0 引言

中國陸地大地基準網建設已經相對完善，并且長期復測維持，已經具備厘米級精度(陳俊勇等，2007；楊元喜，2009；魏子卿，2008；魏子卿等，2011).北斗導航系統的建成并以其短報文通信服務、位置跟蹤和精密單點定位功能進一步為陸地及水面用戶提供了很大的幫助(楊元喜等, 2017；Yang et al., 2020).由于電磁波在水中的衰減速度較快，無法遠距離傳播，基于電磁波為信號載體的衛星導航技術無法適用于水下導航或定位，因此如何精確獲取水下三維坐標位置，一直是實現真正意義上“全球”大地測量道路上的一道關卡.20世紀80年代，美國Scripps Institution of Oceanography的Spiess提出了全球衛星導航系統-聲學定位技術(GNSS-A)，利用全球衛星導航系統獲取海面上的坐標，通過水下聲學定位技術，將大地基準網延伸至了海底，為海底控制點高精度定位提供了一個可行的解決思路(Spiess,1985).

GNSS-A技術除了需要解決聲學測距系統硬件、動態定位等技術上實現的困難外，還需要設計最優觀測構型和定位模型以解決待估參數強相關性問題.例如，聲速系統誤差與垂直分量之間存在強相關性(Watanabe et al., 2020)、GNSS接收機與聲學換能器之間偏移參數的垂直分量與海底控制點的垂直分量之間存在參數強相關(Chen et al., 2019; 馬越原等，2021).聲波在海水中的傳播路徑存在聲線彎曲，進而引起測距偏差，這種偏差與復雜的海洋環境和聲線入射角有關(趙建虎和梁文彪, 2019)；此外，聲速測量值還存在時空變化特性，即同一空間不同時間或同一時間不同空間所測得的聲速信息是不同的，時空變化特性是由聲波自身的物理特性以及不斷變化的海洋環境特性造成的(劉伯勝和雷家煜，2010).這種聲線彎曲引起的測距誤差可以利用聲線跟蹤算法進行修正(李圣雪等, 2015; 王振杰等, 2016; Sakic et al., 2018; 辛明真等，2020)，但該方法非常費時.如在海底定位測量期間獲得海域的聲速場，可以將它們引入到定位模型中進行估計，再在此基礎上施加聲線彎曲與延遲改正(Wang et al., 2020).對于時變引起的聲速誤差，則可以借鑒GNSS大氣誤差處理，發展海底基準網動態數據處理模型予以削弱(Yang et al.，2020).也有學者提出了一種廣義的系統誤差補償的彈性模型(楊元喜，2018；Yang and Qin，2021)，即根據不同的誤差影響對函數模型進行彈性調整以減少系統誤差對定位精度的影響，提高了定位結果精度.

目前，GNSS-A技術在日本的應用最為廣泛，由于日本地理位置的特殊性，該技術主要用于揭示俯沖帶的構造過程、監測地殼形變，特別是在西北太平洋和日本南開海槽(Yokota et al., 2016; Yasuda et al., 2017; Yokota and Ishikawa, 2019)和日本海溝(Kido et al., 2011; Watanabe et al., 2014; Tomita et al., 2017)處應用較多.然而，在這些研究中，都是由多個聲學應答器組成，在海底對稱布放，然后確定陣列中心(一個虛擬點)，最后估計陣列位置之間的相對變化(Gagnon and Chadwell, 2007; Yokota et al., 2016; Watanabe et al., 2020).這種基于虛擬點所得到的研究結果在監測地震、板塊運動等問題上具有很大的意義，但是其更注重陣列的整體變化，并沒有得到各個聲學應答器的精確位置，所以是無法在此基礎上構建海底基準網.因此，為了切實可行的將陸地大地基準網延伸至海底，保證水下用戶的定位和導航，基于單個固定站和多個錨系站的GNSS-A技術被提出(Yang and Qin, 2021)，其中固定站用于海底基準的構建，錨系站用于水下用戶的導航(歐陽明達和馬越原，2020).

本文針對上述問題對圓加十字測量模式進行了系統分析，首先詳細介紹了水下定位技術的定位模型及精度評估方法，然后詳細分析了為什么要增加十字觀測的原因以及為什么不單獨使用十字觀測的原因，此后詳細推導了圓加十字測量模式的最佳走航半徑，最后利用實測數據驗證了在圓走航的基礎上增加十字觀測能有效改善垂向幾何結構，提高對海底控制點的定位精度.

1 水下聲學定位模型

水下聲學定位技術的定位模式是基于距離交會原理，基本原理如圖1所示.圖1左下角，為測量船在當地水平坐標系(NEU)中的位置，NEU坐標系是一種地方空間直角坐標系，它的坐標原點在任一選定的測站上，其北向坐標軸(N坐標)為過原點的子午線的切線，指北為正；其東向坐標軸(E坐標)為過原點的橢球的平行圈的切線，指東為正；天頂方向坐標軸(U坐標)為過原點的由N軸與E軸決定的平面的垂線，指向天頂為正(黃立人等，2006).NEU坐標系有助于表示對不同坐標分量的誤差影響(Yang and Qin, 2021)，在本文中均采用當地水平坐標系，并取海底控制點在海面上的投影點為坐標系原點.其中，γ為聲學測距與垂線方向的夾角，β為測量半徑方向與水平坐標系E軸的夾角，水深為h.

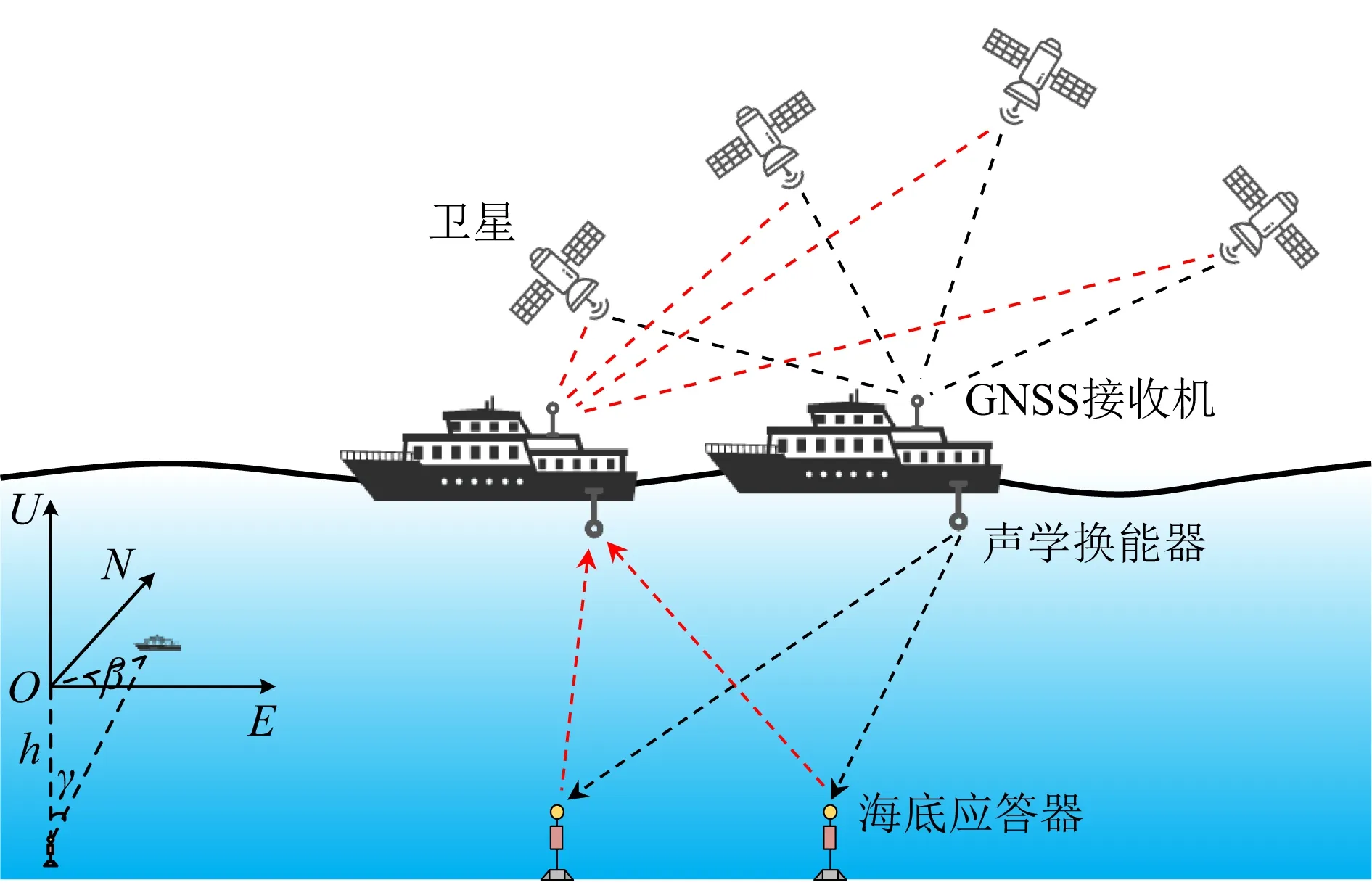
圖1 水下聲學定位技術原理圖Fig.1 Principle of underwater acoustic positioning

首先，通過GNSS定位技術獲取測量船在聲學測距時不同時刻的GNSS天線坐標，利用船載羅經提供的實時姿態數據，將天線坐標轉換為船載換能器的坐標；然后，利用聲學換能器和布設在海底的控制點(聲學應答器)組成的聲學觀測系統測得的聲波傳播時間以及聲速剖面，可以計算出聲學換能器和應答器之間的幾何距離.考慮到聲波在傳播過程中，測量船并不是靜止的，因此，在NEU坐標系中，水下聲學定位的定位模型可以寫成(Xu et al., 2005; Ribeiro et al., 2015; 曾安敏等，2021)：

ci·ti=ρf,i+ρb,i+δρd,i+εi,

(1)

(2)

(3)

式中，ti表示第i個歷元聲學測距所測得的雙程傳播時間；ci表示ti期間聲波在海水中傳播的等效聲速；ρf,i和ρb,i分別表示發射時刻和接收時刻換能器和海底應答器之間的幾何距離；nf,i、ef,i和uf,i表示發射時刻換能器的三維坐標；nb,i、eb,i和ub,i表示接收時刻換能器的三維坐標；nseafloor、eseafloor和useafloor表示待估的海底應答器的三維坐標；δρd,i表示由換能器安裝校準偏差、應答器響應誤差、聲速擾動引起的測距系統誤差；εi表示隨機誤差，包含聲學時延測距誤差、換能器坐標的有色和白色噪聲.

將式(1)通過泰勒級數展開后，水下聲學定位模型的誤差方程可以表示為：

(4)

(5)

(6)

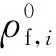
(7)

vi為第i個歷元計算得到的觀測量殘差.

對于n個觀測歷元，可以列出誤差方程組：

(8)

式(8)的矩陣形式可以表示為：

V=A·dX-L.

(9)

根據式(9)和最小二乘準則，可以得到未知參數的改正數為：

dX=(ATPA)-1·(ATPL)=N-1·U,

(10)

式中，N為法矩陣；P為觀測量的權矩陣.

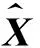
(11)

(12)

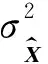
從式(12)可以看出，未知參數的協方差矩陣是由觀測方程殘差和法矩陣組成的函數，所以未知參數協方差矩陣的值可以反映出觀測量的全部幾何信息以及未建模誤差的大小.因此可以通過優化測量航跡的幾何構型和定位解算模型來提高GNSS-A技術的定位精度(Sato et al., 2013; Chen et al., 2020).

2 直線測量模式分析

2.1 直線測量模式參數可估性

Chen和Wang(2007)給出了一種基于隱函數的直線測量模式數值分析方法，本文從三角函數的角度出發給出另一種分析思路.直線航跡，可認為是由n個相同圓心的圓嵌套而成，如圖2所示.假設測量船是精確的沿著直線航跡走航，則可以認為每個歷元βi保持不變，因此直線測量模式定位模型誤差方程中的設計矩陣Aline可以表示為：

(13)

在式(13)中，若將Aline矩陣中的每一列元素同時除以cosβ，則可以看出，矩陣中第一列元素和第二列元素存在明顯的線性關系，且系數為常數tanβ，因此矩陣Aline的秩為2，其法矩陣N不可逆.這些分析結果表明，若以一條單一的直線航跡進行聲學定位，則海底控制點的坐標存在無窮多個解，即式(9)沒有唯一解.

圖2 直線測量模式示意圖Fig.2 Straight-line survey pattern

若要解決該問題，只需要沿著兩條或者多條不同的直線航跡進行聲學測距.假設另一條直線航跡與水平坐標系E軸的夾角為α，且走航距離相同，由此可建立的定位模型誤差方程中的設計矩陣Aline可以表示為：

(14)

從式(14)可以看出，若α≠β，則矩陣Aline的秩為3，法矩陣N可逆.說明只有當沿兩條或者多條直線航跡進行聲學定位時，才可以唯一確定海底控制點的三維坐標.

2.2 十字測量模式的最優幾何構型

圓形測量模式由于其特殊的幾何結構導致在估算海底控制點三維坐標時，垂直分量的精度被弱化(Chen et al.,2020).若要保證垂直分量的精度，則需要測量船過頂觀測.而為了同時獲得幾何上良好的對稱，十字交叉的測量模式(Yang et al.，2020；Chen et al.,2020)是一種可行的測量方式，即由兩條交叉且垂直并經過海底控制點頂部的直線航跡所構成的觀測圖形，如圖3所示.

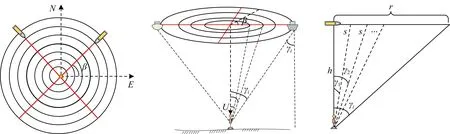
圖3 十字航跡示意圖Fig.3 Schematic diagram of cross-track

直線走航不同于圓走航，在于圓走航時每個歷元聲學換能器相對海底控制點的距離幾乎相等，因此可以認為觀測量之間獨立等精度，在解算時可以認為權矩陣P為單位陣；但是直線走航時每個歷元聲學換能器相對海底控制點的距離都是不同的，所受隨機誤差的影響不同，因此直線走航時可采用顧及聲線入射角的定權模型或其他定權模型來確定權矩陣(趙爽等, 2018；Wang et al., 2019；孟慶波等，2019).但為了公式的推導簡潔明了，在本文中我們依然采用單位權矩陣進行分析(在實際解算時不宜使用單位權).

(15)

根據三角函數誘導公式，可得：

(16)

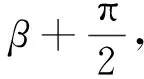
(17)

根據三角函數誘導公式，可得：

(18)

由式(16)和(18)可以得十字航跡的設計矩陣Acr為：

(19)

根據式(19)則可得到十字航跡的法矩陣Ncr為：

(20)

利用法矩陣Ncr可以得到滿足航跡最優幾何結構的條件，tr(N-1)反映了位置精度(Zhao et al., 2013, 2016; Moreno-Salinas et al., 2016; 曾安敏等, 2021)，tr(N-1)的平方根為位置精度因子(PDOP)，即水平精度因子(HDOP)和垂直精度因子(VDOP)之和的平方根，表示為：

PDOP2=HDOP2+VDOP2.

(21)

在單位權方差因子一定的情況下，要想點位精度最高，則位置精度因子要最小.

法矩陣N的對角線元素之和等于采樣數(Zhao et al., 2016；孫文舟，2019；曾安敏等，2021)，即：

(22)

要PDOP2取最小值，則可對其構造Lagrange函數：

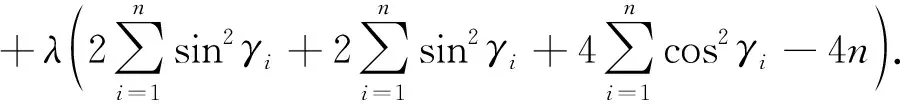
(23)

根據極值求解規則，可得：

(24)

即有：

(25)

式(25)中γ1,γ2,…,γn的幾何關系如圖3所示.因為測量船在走航時是勻速的，且采樣間隔是固定的，所以假設一次采樣間隔期間，測量船的走航距離相等且為s，則有：

(26)

那么式(25)可以寫成：

(27)

式(27)中，h和s在實際測量中都為固定值，此時只需得到采樣數n，就可以得到最優的走航長度.因為ns=r，利用Matlab工具可以解算得到十字航跡的最佳走航長度為：

r≈4h.

(28)

2.3 直線測量模式

從前面的分析可以看出，若要得到最優的海底控制點三維點位精度，在3000 m水深的情況下，走航長度要達到10 km以上，而一般用來進行聲學測距系統的工作距離大概為10 km，距離越遠，觀測數據的質量將大幅降低，因此，十字航跡在大多數情況下不會單獨用來進行海底控制點的絕對定位.此外，十字測量模式主要是為了改善圓形測量模式定位的垂向幾何結構，所以十字測量模式通常是與圓形測量模式組合應用的，形成常見的圓加十字測量模式，如圖4所示.

圖4 圓加十字航跡示意圖Fig.4 Schematic diagram of circular track plus cross-track

直線測量模式較圓形測量模式最顯著的特點表現在，直線測量模式設計矩陣中垂直分量的系數是不斷變化的，而圓形測量模式設計矩陣中垂直分量的系數幾乎保持不變，若將測量時所受到的測距系統誤差看作一個待估參數且系數為1，則直線測量模式無需附加先驗信息就能較好地將系統誤差參數分離，因此采用直線測量模式進行水下聲學定位時，海底控制點垂直分量所受到測距系統誤差影響較小，從而滿足垂直分量精度的要求.直線測量模式最大的優點在于實際測量時便于測量船的控制，圖形規則.但是沿著一條規則的直線進行測量時無法得到唯一的海底控制點三維坐標，至少需要沿著兩條直線進行測量，才能得到唯一解.

有文獻指出，若要使垂直分量精度最高，應在水聲應答器的過頂方向進行重復觀測(曾安敏等，2021).前文已經提到，幾何上平衡且對稱的復雜觀測航跡有助于約束垂直方向所受到的誤差影響，有利于監測聲速結構的水平不均一性.因此，作為增強圓形測量模式垂向幾何結構的補充圖形，綜合考慮測量船的控制，圖形結構的對稱性，是否過頂觀測以及增加采樣數所產生的經濟效應等多種因素，較兩條平行直線圖形、交叉非垂直圖形、幾橫幾豎交叉網圖形等其他由直線組成的觀測圖形而言，十字測量模式是最優選擇.

3 圓加十字測量模式最優幾何構型分析

假設圓形測量模式的直徑剛好為十字測量模式的長度，且采樣數為m，因為測量船的采樣間隔固定，假設十字測量模式的采樣數為4n，則n和m之間的關系為：

(29)

圓形測量模式的法矩陣Ncircle可寫為(孫文舟，2019；曾安敏等，2021)：

(30)

如此，圓加十字測量模式的法矩陣Nccr可寫為：

(31)

可以看出，圓加十字測量模式下垂直分量的幾何結構變得更好，其方差明顯小于圓形測量模式的方差，垂直分量精度將會更高.同式(22)，法矩陣Nccr的對角線元素之和為m+4n.所以要PDOP2取最小值，對其構造Lagrange函數可以解得：

(32)

根據圖4中的幾何關系，式(32)可以寫成：

(33)

同樣水深h和s均為固定值，因為ns=r，可以得到圓加十字測量模式的最佳走航半徑為：

r≈1.15h，

(34)

4 實測數據分析

為了驗證增加十字測量模式能有效改善圓形測量模式的垂向幾何結構，提高定位精度，本文采用南海實測數據進行分析.本次實驗數據的采集時間為2021年5月3日至5月4日，實驗地點在南海海域，實驗搭乘“向陽紅18號”科考船參與數據采集.船上搭載星基差分接收機、姿態測量儀、自容式SVP以及DP系統.其中星基差分接收機能夠提供星基差分服務，獲得的測量船軌跡精度優于0.5 m；姿態測量儀的采樣頻率為5 Hz，精度優于0.01°；自容式SVP的測量精度優于0.1 m·s-1；DP系統能夠保證在布設海底控制點和測量聲速剖面時，測量船的位置不發生改變.在測量過程中，船速不超過3 kn.此次實驗測區水深約3000 m，海底地形較為平坦，海況良好.

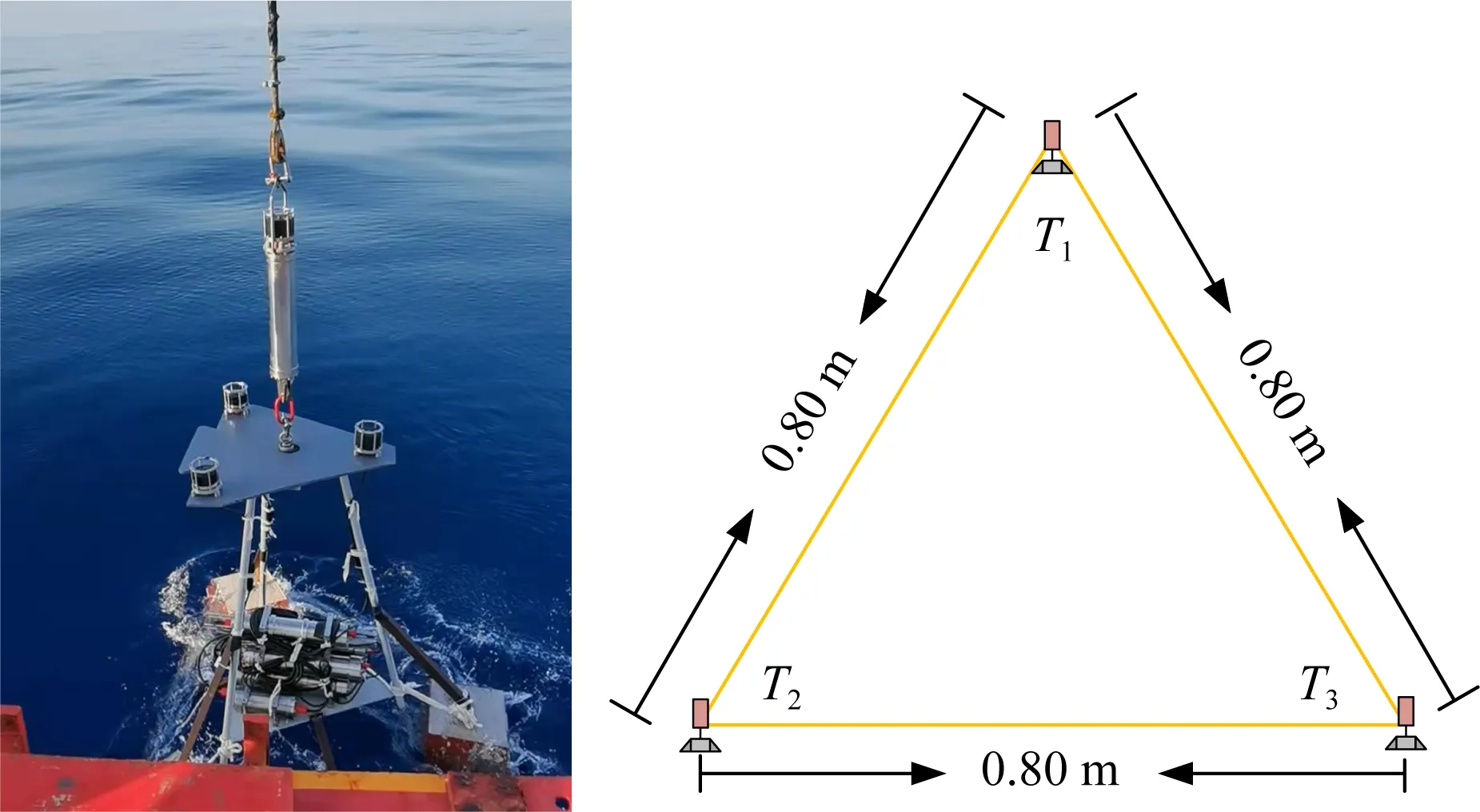
圖5 海底控制點及信標布放位置示意圖Fig.5 Schematic diagram of seafloor control point and beacon placement position on the station

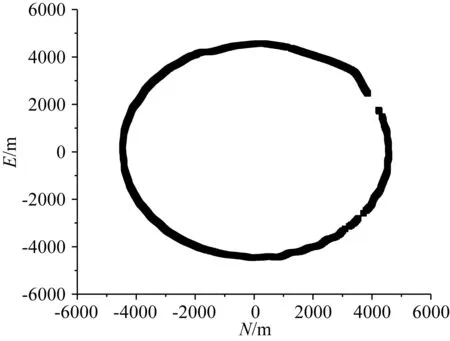
圖6 圓形航跡Fig.6 Circular track

圖7 圓加十字航跡Fig.7 Circular track plus cross-track

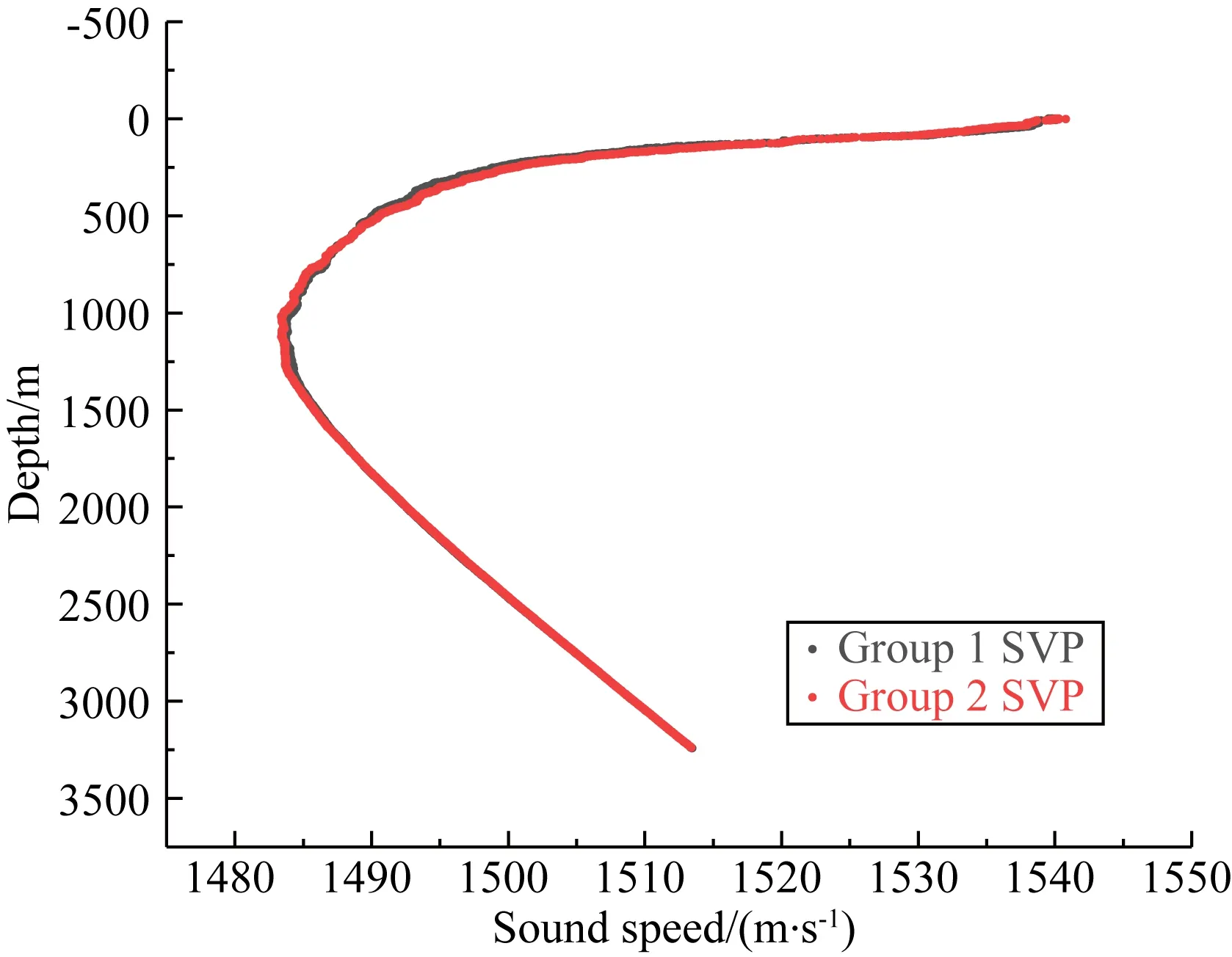
圖8 聲速剖面Fig.8 Sound velocity profile

此外，為了驗證增加十字航跡能有效提高圓形測量模式的垂向精度，由于布設的海底控制點沒有已知的坐標值，本文采用其他日期的觀測數據解算的結果作為外部檢核值.其中T1的采樣數為4875，T2的采樣數為5043，T3的采樣數為4937，解算的垂向坐標分別為-3253.49 m，-3253.54 m，-3253.46 m.這批觀測數據的采樣數遠遠多于圓形航跡和圓加十字航跡的采樣數，在解算方法一致的情況下，理論上來講坐標解算精度更高，因此本文將該結果稱為參考值.

分別解算圓形航跡和圓加十字航跡中水聲應答器T1、T2、T3的坐標，計算結果如表1所示.

表1 不同航跡定位結果Table 1 Positioning results by different track

表1中，N、E、U分別為當地水平坐標系中的北向分量、東向分量和垂直分量，σn、σe、σu分別為N、E、U分量的內符合精度.可以看出圓形測量模式和圓加十字測量模式之間的差值在0.1 cm左右，兩種方案計算的點位坐標結果差異較小.但是僅從內符合精度無法看出圓加十字測量模式相比于圓形測量模式對海底控制點定位精度的提升.

由于水聲應答器T1、T2、T3之間存在一個固定基線長0.80 m，可以利用不同航跡解算得到的T1、T2、T3的坐標位置來求得它們之間的幾何長度，與外部參考值進行比較，從而來評估圓形航跡和圓加十字航跡的定位精度.表2為外部參考值0.80 m與應答器坐標反算的距離之間的偏差.其中圓形航跡解算的結果差值最大為0.068 m，最小為0.016 m，平均偏差為0.041 m；圓加十字航跡解算的結果差值最大為0.029 m，最小為0.026 m，平均偏差為0.027 m.

表3為水聲應答器的垂直坐標解與參考值之差，其中圓形航跡解算的垂直坐標與參考值之間的最大偏差為0.57 m，最小為0.44 m；圓加十字航跡解算的垂直坐標與參考值之間的最大偏差為0.47 m，最小為0.40 m.這些結果進一步說明了增加十字航跡能有效改善圓形測量模式的垂向幾何結構，提高對海底控制點的定位精度.

表2 水聲應答器之間的真實值和坐標計算值之差Table 2 Difference between the true value of the transponder and the calculated value of the coordinates

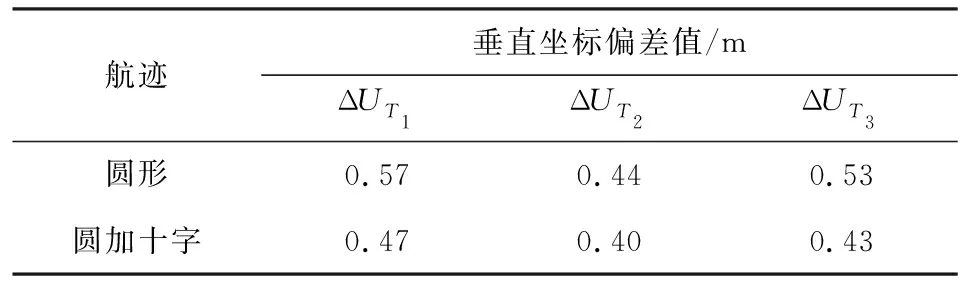
表3 水聲應答器的垂直坐標偏差值Table 3 Vertical coordinate deviation of transponders

5 結論

本文針對直線走航，提出了一種基于嵌套圓的新的分析方法，從數學上證明了采用直線測量模式時至少需要兩條直線來進行測量，才可以唯一確定海底控制點的三維坐標.在此基礎上，對廣泛提出的十字測量模式進行了系統分析，從理論上推導了采用十字測量模式時獲得最優海底控制點三維點位精度的走航長度為8倍水深，若在深海測量時，現有的聲學測距設備無法滿足該條件.此外，從理論上證明了圓加十字測量模式的最優測量半徑，并用實測數據驗證了在圓走航的基礎上增加直線走航能有效改善定位的垂向幾何結構，提高海底控制點的定位精度.并且，該理論分析方法不僅適用于圓加十字測量模式，任何由圓或者直線組成的測量軌跡均可利用該方法進行分析，從而在實驗之前得到預設軌跡的最優走航半徑(長度).

本研究充分說明了海底控制點的定位精度與測量船走航軌跡密切相關，不同航跡具有不同的幾何分布，有助于獲得幾何上良好平衡的觀測數據，同時有助于約束垂直運動和減小聲速結構誤差的影響.

需要指出的是，并不存在所謂的唯一最優航跡，但是，優化測量航跡不僅能提高海底定位精度，同時能提高觀測效率.

致謝特別感謝國家重點研發計劃“海洋大地測量基準與海洋導航新技術”項目組及深海試驗全體科研人員的合作與支持.