偶極橫波遠探測在裸眼井及套管井中接收波場的方位響應特征

李楊虎， 唐曉明,3*， 蘇遠大,3

1 中國石油大學(華東)地球科學與技術學院， 青島 266580 2 中國石油大學(華東)深層油氣重點實驗室， 青島 266580 3 青島海洋科學與技術國家實驗室海洋礦產資源評價與探測技術功能實驗室， 青島 266071

0 引言

近年來，偶極橫波遠探測成像測井技術取得長足發展，其在裂縫、斷層、溶蝕孔洞等地質構造的探測中取得了良好的應用效果.Tang(2004)于2004年首次提出了偶極橫波遠探測成像方法，該方法通過充液井中的偶極聲源向地層輻射橫波，并在井中接收經反射體反射回來的橫波進行井周成像.與常規的單極縱波法相比(Hornby, 1989; 薛梅, 2002; 喬文孝等, 2004; 陶果等, 2008)，偶極橫波法具有以下優勢：一、偶極聲源具有方位靈敏度，采用多分量發射和接收可以確定反射體的走向；二、偶極聲源的工作頻率為3 kHz左右的低頻，因而其徑向探測深度更深.此后，國內外學者針對偶極橫波遠探測技術開展了大量的研究工作，其現已成為非常規油氣勘探中尋找油氣甜點的利器(Tang and Patterson, 2009; 唐曉明和魏周拓, 2012; 蘇遠大等, 2014; Tang et al., 2014, 2016; Hirabayashi et al., 2017; 宮昊等, 2018; Bennett, 2019; Lee et al., 2019; Xu et al., 2019; 董經利等, 2020; 古希浩等, 2020; 劉匯鑫等, 2021).

研究井孔對聲場的調制作用對偶極橫波遠探測具有重要意義，包括井內偶極聲源在地層中的輻射特性以及井孔對入射波的方位接收響應.對于偶極聲源在井外的輻射聲場，國內學者已經做了充分研究.Tang等(2014)給出了偶極聲源在井外無限大地層中輻射橫波的位移遠場漸近解及其輻射指向性表達式.在此基礎上，曹景記等(2014)和唐曉明等(2019)研究了偶極聲源在裸眼和套管井外的橫波輻射特征，并證實了在套管井中進行偶極橫波遠探測的可行性.井孔對入射波的接收響應可分為平面波和球面波入射兩種情況，對于平面波入射引起的井內聲場的方位響應，人們已經進行了深入研究，見White(1953)、Schoenberg(1986)、Peng等(1993)以及Hirabayashi等(2017)發表的研究成果.然而，聲波遠探測中入射波場是以球面波的形式向井孔傳播，對于球面波入射引起的井內聲場的方位響應尚未做深入研究.雖然前人能夠對偶極橫波遠探測的接收聲場進行快速模擬(Tang et al., 2014; 許家旗和胡恒山, 2019)，但這些研究中都使用了互易定理來求解井孔的球面波入射響應，該方法主要用于分析井中聲源和接收器位置同軸線的情況，不能對實際測井時儀器接收到的方位波場進行有效模擬.針對此，Li等(2021)在虛源法的基礎上，結合柱面波展開法(Tang and Cheng，2004)，求解得到了充液裸眼井中偶極橫波方位遠探測接收聲場的解析解，為方位聲波遠探測的模擬奠定了理論基礎.

目前，利用偶極橫波遠探測進行井周成像或反射體方位識別的相關方法主要是根據井中接收波形的幅度變化特征(Tang and Patterson, 2009; Hirabayashi et al., 2017; 李盛清等, 2020; 許家旗和胡恒山, 2020; Li et al., 2021)，但充液井中遠探測波場的方位接收響應還缺乏詳盡的理論分析.因此，對偶極橫波遠探測聲場在井內流體中產生的徑向位移和聲壓的方位響應特征進行深入研究具有重要意義.另一方面，基于全球各地油田中套管井的大量存在以及被證實的過套管偶極橫波遠探測的可行性(唐曉明等, 2019)，本文將裸眼井中遠探測聲場的方位解析解延展到套管井中，研究了不同膠結情況套管井中接收波場的方位響應特征，并與裸眼井情況進行了對比分析.最后，利用三維有限差分法證實了聲場幅值方位響應中的180°反轉現象.本文的研究對偶極橫波遠探測測井時裸眼和套管井中接收聲場的方位響應特性有了更為全面的認識，為偶極橫波方位遠探測的技術發展、儀器研制以及現場解釋提供了理論支持.

1 充液井中偶極橫波方位遠探測接收聲場的解析解

圖1a給出了當井外存在反射體時，充液裸眼或套管井中偶極聲波遠探測模擬所用的坐標系.在測井儀器的偶極聲源上方環向布置了多組偏心距為e的接收器，其接收橫截面如圖1b中模型所示.按照不同的聲源—接收器組合方式，可模擬不同的測量工作模式，如正交偶極發射—正交偶極接收模式，正交偶極發射—多方位接收模式，本文采用多方位接收模式對井中接收波場的方位響應進行研究.偶極聲波遠探測包含三個過程，即充液井孔內偶極聲源在井外的輻射、井外地質體的反射以及充液井孔對反射波的接收調制.在輻射距離遠大于波長的遠場輻射條件下，圖1a中偶極聲源輻射到地層中的SH和SV橫波位移勢函數和Γ的遠場漸近解為(唐曉明和魏周拓, 2012)：

(1)

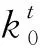
當輻射橫波與地層中的反射體作用后，可將反射回井孔的入射橫波波場表示為(Tang et al., 2014, 2016)：

(2)

式中，RD為聲源在井外遠處的輻射函數，由式(1)的中括號里的部分組成；RF為聲波在反射體處的反射系數，可由佐普利茲方程求得(Aki and Richards,

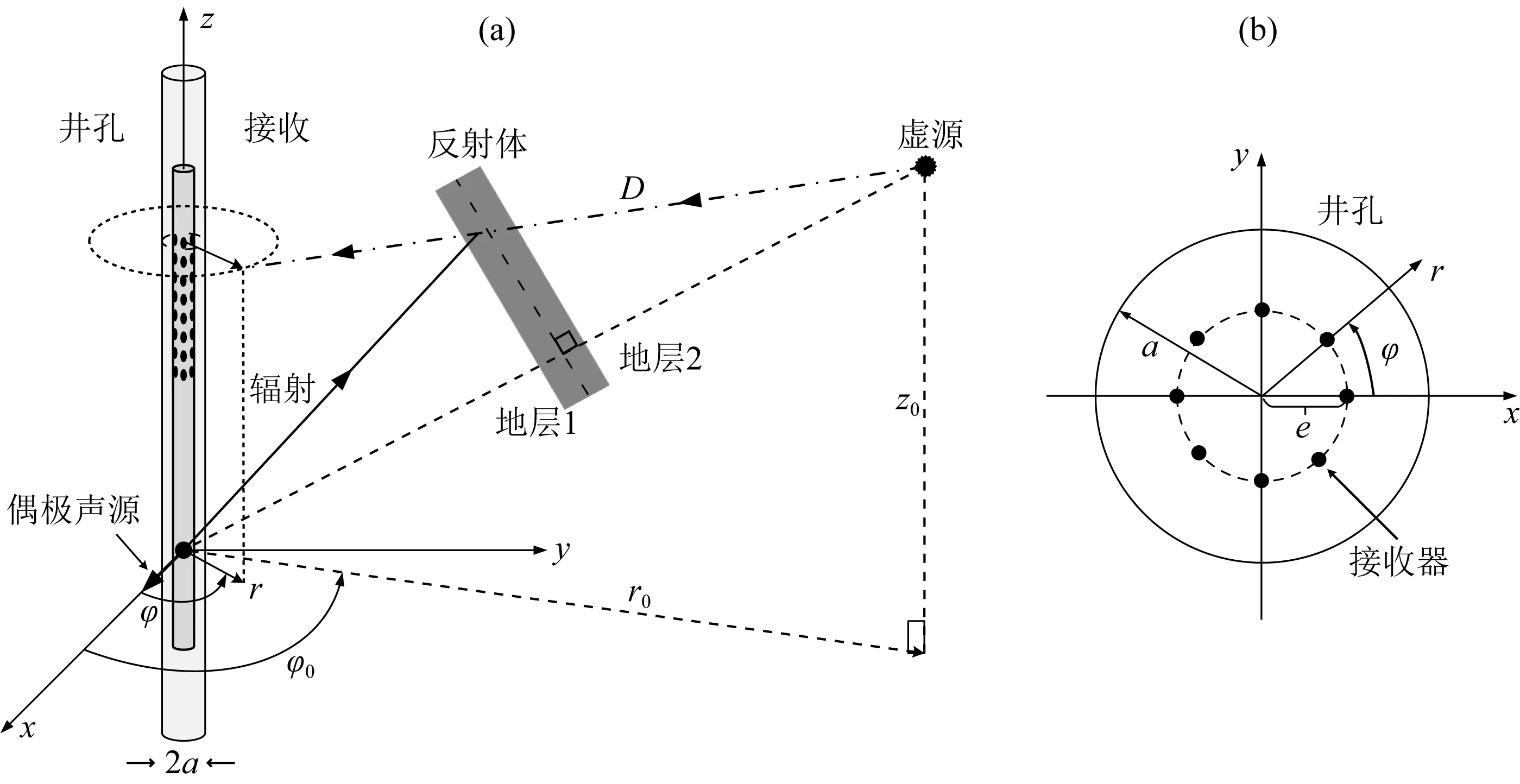
圖1 基于虛源法的偶極聲波遠探測示意圖(a)及方位接收井孔截面示意圖(b)Fig.1 The schematic model of dipole single-well reflection imaging based on the virtual source analogy (a) and the cross section of borehole receiving configuration using azimuthally spaced off-axis receivers (b)

1980)；S、RD、RF都是關于圓頻率ω的函數；D為聲波在地層中總的傳播距離，其傳播路徑為一條折線.Li等(2021)通過將遠探測聲場看作是聲源在反射體向外一側的鏡像點的輻射聲場，此時聲波的傳播路徑D轉化為一條直線，如圖1a中所示，從而式(2)中的球面波傳播因子可以展開為多極子柱面波疊加的形式(唐曉明和鄭傳漢, 2004)：

×eik(z-z0)dk，

(3)

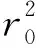
將式(3)代入式(2)，對于圖1a中所示的偶極聲源指向，入射SH和SV橫波的位移勢函數表達式為：

×cos[n(φ-φ0)],

(4)

其中，上標i表示入射波場；下標SH和SV表示計算聲源的輻射函數RD和反射系數RF時應分別對應SH和SV橫波.

考慮徑向包含多層的井眼模型，假設井壁與地層之間共有N-1圓柱層，其中第m層為固體層，第j層為液體層.當入射橫波與井眼相互作用時，根據赫姆霍茲方程，在柱坐標系(r,φ,z)下井內流體中的位移場uf、第j層流體中的位移場uf(j)和第m層固體中散射波的位移場us(m)分別為：

(5)

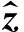
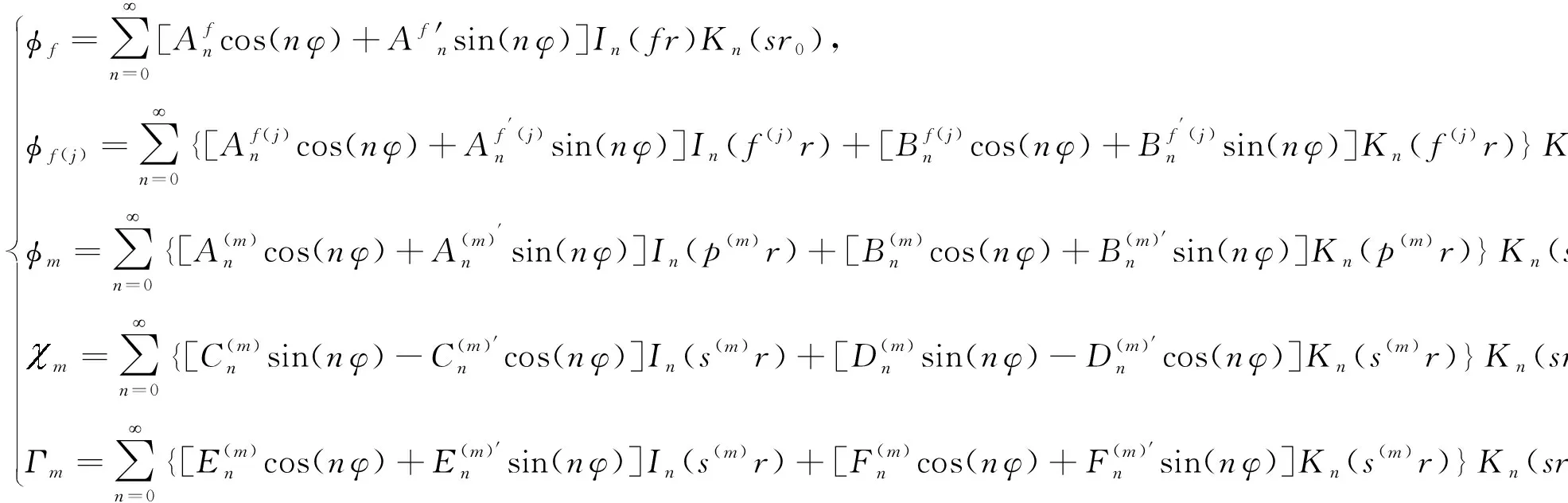
(6)

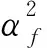
在裸眼井情況下，式(5)中的模型由井內流體和地層兩部分組成，此時井壁處的邊界條件為：徑向位移和正應力連續，環向和軸向的剪切應力為零，表達式為：

(7)

式中，a為井孔半徑；上標s和f分別表示地層中的散射波場和流體中的透射波場.

由式(4)、(5)、(6)計算出入射波、散射波和透射波的位移和應力，代入式(7)的邊界條件得到兩個矩陣方程：

(8)

為了便于描述，將式(8)中方程左側與井中透射波和地層中散射波有關的矩陣記為矩陣M，右側與地層中入射波有關的向量分別記為向量b和b′.矩陣M，向量b和b′中的元素表達式詳見附錄A.

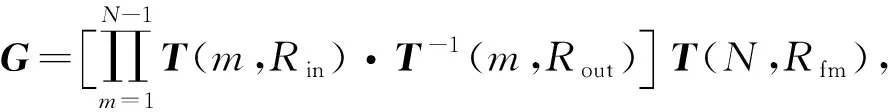
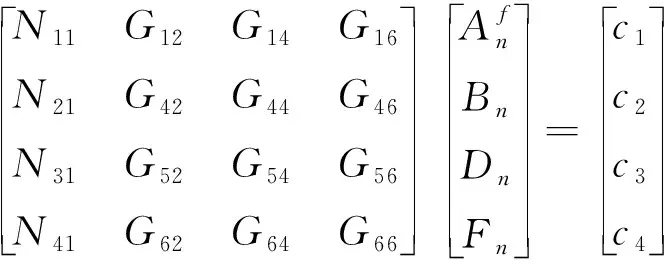
(9)

其中，矩陣元素N11～N41及向量c和c′可由方程(8)中與之相對應的部分將井孔半徑置換為套管內徑后得到；G矩陣為6×6階復數矩陣，計算G矩陣所用到的T矩陣的元素表達式詳見附錄B.

在套管和地層之間添加一流體層來模擬自由套管的情況，此時由井中流體-套管-流體環-地層組成的模型中所包含的3個界面均為流-固界面.與固-固界面不同，對流-固界面的每一個邊界條件都要單獨進行處理，通過連接邊界條件，最后整合得到矩陣方程：

(10)

式中，H為12×12矩陣，d和d′為12×1向量；系數向量中的上標1、2和3表示該振幅系數分別對應套管、流體環和地層介質.矩陣H，向量d和d′中的元素表達式詳見附錄C.

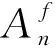
(11)

其中，ρf為流體密度.對于遠場輻射，虛源的徑向距離r0遠大于彈性波的波長，滿足|sr0|?1的條件，由此可對式(11)中的波數積分運用最速下降方法求解(Tang and Patterson, 2009; Li et al., 2021)，整理得到：

(12)

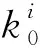
(13)

式(13)指出，井軸上接收到的流體聲壓只有單極項(n=0)貢獻，而徑向位移只有偶極項(n=1)貢獻.

綜上所述，利用式(12)和式(13)便可計算偶極橫波遠探測聲場在裸眼和套管井情況下所引起的井內流體的徑向位移和聲壓的方位響應.

2 算法對比驗證及分析

我們首先利用三維有限差分法驗證上述解析解的正確性，采用膠結良好的套管井模型.計算所用的井孔及地層參數如表1所示，其中反射體設為地層1和地層2之間傾角為45°的界面，位于0°方位，虛源的徑向距離為10 m.聲源上方1 m處共有8個接收器間隔45°環向布置，接收器的偏心距離均為0.035 m.聲源采用中心頻率為3 kHz的Ricker子波，差分模擬時的空間網格和迭代時間步長分別為0.005 m和0.48 μs.

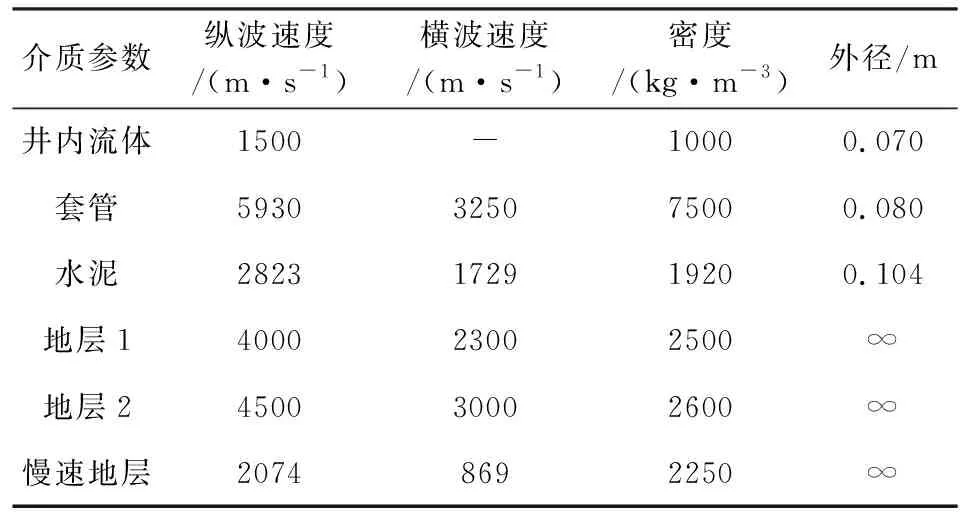
表1 模型計算參數Table 1 Model parameters for calculation

通過將偶極聲源指向y(x)來模擬SH(SV)橫波入射，圖2和圖3給出了對比結果.其中，虛線為有限差分計算的結果，實線為解析解計算的結果.由于有限差分法模擬的是井內和井外的全波波場，而解析解式(12)只模擬了井外的反射波部分，因此圖2和圖3中只顯示了反射橫波的到時區間.當聲源指向y向時，產生純SH入射波.從圖2中可以看出，無論是井內流體的徑向位移(圖2a)還是聲壓(圖2b)，采用解析解得到的漸近結果與有限差分模擬的數值結果幾乎完全重合，這說明解析解是準確可靠的.圖2中也顯示出了井中接收波形的方位特征：當接收器指向與反射體走向平行(即90°和270°)時，接收到的徑向位移和聲壓的幅度最大；而當接收器指向垂直于反射面(即0°和180°)時，接收不到徑向位移和聲壓；此外，x軸上下兩側接收到的徑向位移和聲壓的極性均反生反轉.上述分析表明，SH橫波入射引起的井內流體的徑向位移和聲壓響

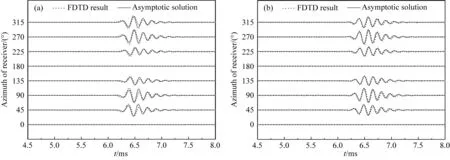
圖2 SH橫波入射引起的井內流體響應的漸近解(實線)和三維有限差分(虛線)的計算結果對比(a) 徑向位移； (b) 聲壓.Fig.2 Comparison of the borehole-fluid response calculated using the analytical solution (solid curves) and the 3D finite-difference method (dashed curves) for SH-wave incidence(a) Radial displacement; (b) Pressure.

應對井外反射體方位的靈敏度高，且兩者特征具有較好的一致性，說明在進行遠探測時采用反射波中的SH分量更具優勢；但該分析也表明了其存在的180°方位不確定性.

當聲源指向x向時，利用解析解式(12)計算的是純SV橫波入射，但實際上聲源在產生SV橫波的同時還會產生P波入射，因此有限差分結果中還包含一些小振幅的P-SV和SV-P轉換波(如圖3中4.5～5.5 ms所示).盡管如此，圖中顯示兩種方法計算的SV橫波反射結果吻合較好.與圖2中SH橫波的入射結果相比，SV橫波入射引起的井內流體的徑向位移和聲壓的方位特征存在較大差異.對于徑向位移而言(圖3a)，當接收器靠近反射體時接收到的幅度最大，當接收器指向平行于反射面(即90°和270°)時接收到的幅度最小但不為零；y軸左右兩側接收到的位移的極性反生反轉.而聲壓(圖3b)則表現出較強的方位性，靠近反射體的接收器接收到的聲壓幅度最大，并且不同方位接收的聲壓極性相同.結果表明，在進行遠探測時，考慮反射波中的SV分量有助于識別井外反射體的方位.

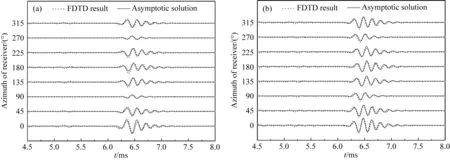
圖3 SV橫波入射引起的井內流體響應的漸近解(實線)和三維有限差分(虛線)的計算結果對比(a) 徑向位移； (b) 聲壓.Fig.3 Comparison of the borehole-fluid response calculated using the analytical solution (solid curves) and the 3D finite-difference method (dashed curves) for SV-wave incidence(a) Radial displacement; (b) Pressure.

在套管井復雜模型下所表現出的良好的吻合性，驗證了解析解的正確性和普適性.然而，兩種方法的計算效率相差很大，為了更準確地模擬接收器的偏心效應以及套管的影響，在三維有限差分建模中必須使用毫米級的網格尺寸，這需要花費數10 h才能完成模擬.相比之下，式(12)的解析解只需要數秒便可以得到準確的結果，為偶極橫波方位遠探測提供了一種快速高效的模擬方法.

為了進一步詳細考察圖2和圖3中所示波形的方位響應特征，我們增加了接收器的個數并縮小其環向布置間隔.考慮到偶極橫波反射成像中存在的180°方位不確定性問題，圖4和圖5的極坐標圖分別給出了SH和SV橫波入射時兩個相反反射體方位(φ0=0°，180°)的計算結果(圖中實線)，其他參數與圖2中相同，結果按不同方位接收波形的最大幅值進行歸一化處理.如極坐標圖中所示，其結果在0°～180°和180°～360°之間具有對稱性，因此直角坐標系中只顯示了0°～180°的結果.為了對比，同時模擬了當接收器居中時(即位于井軸上)接收的結果，如圖中虛線所示.從圖4中可以看出，對于SH橫波入射，接收器居中時接收到的流體徑向位移的方位幅值響應關于90°和270°對稱，并且接收不到聲壓；而當接收器偏心時，接收到的徑向位移和聲壓的幅度最大值所在方位均由90°和270°向靠近反射體一側偏移.對于SV橫波入射(圖5)，接收器居中時接收到的流體徑向位移和聲壓的方位幅值響應均關于90°和270°對稱，并且聲壓為一常數值；而接收器偏心時接收到的徑向位移的幅度最小值所在方位由90°和270°向靠近反射體一側偏移，并且靠近反射體的接收器將接收到最大幅值的徑向位移和聲壓.接收器居中時聲場響應具有的對稱現象可從式(13)中得到，這種對稱性正是我們所熟知的180°不確定性.相比之下，接收器偏心接收數據所展示出的非對稱性對井外反射體的方位更加敏感，其方位靈敏度有助于解決180°不確定問題.

圖4 對于兩個相反方位的反射體，SH橫波入射引起的井內波場的方位響應(a)、(b) 徑向位移； (c)、(d) 聲壓.Fig.4 The azimuthal response of waveforms inside borehole for SH-wave incidence for the 0° (red) and 180° (black) reflector positions. For comparison, the on-axis result (dashed curves) is also plotted(a) and (b) Radial displacement; (c) and (d) Pressure.

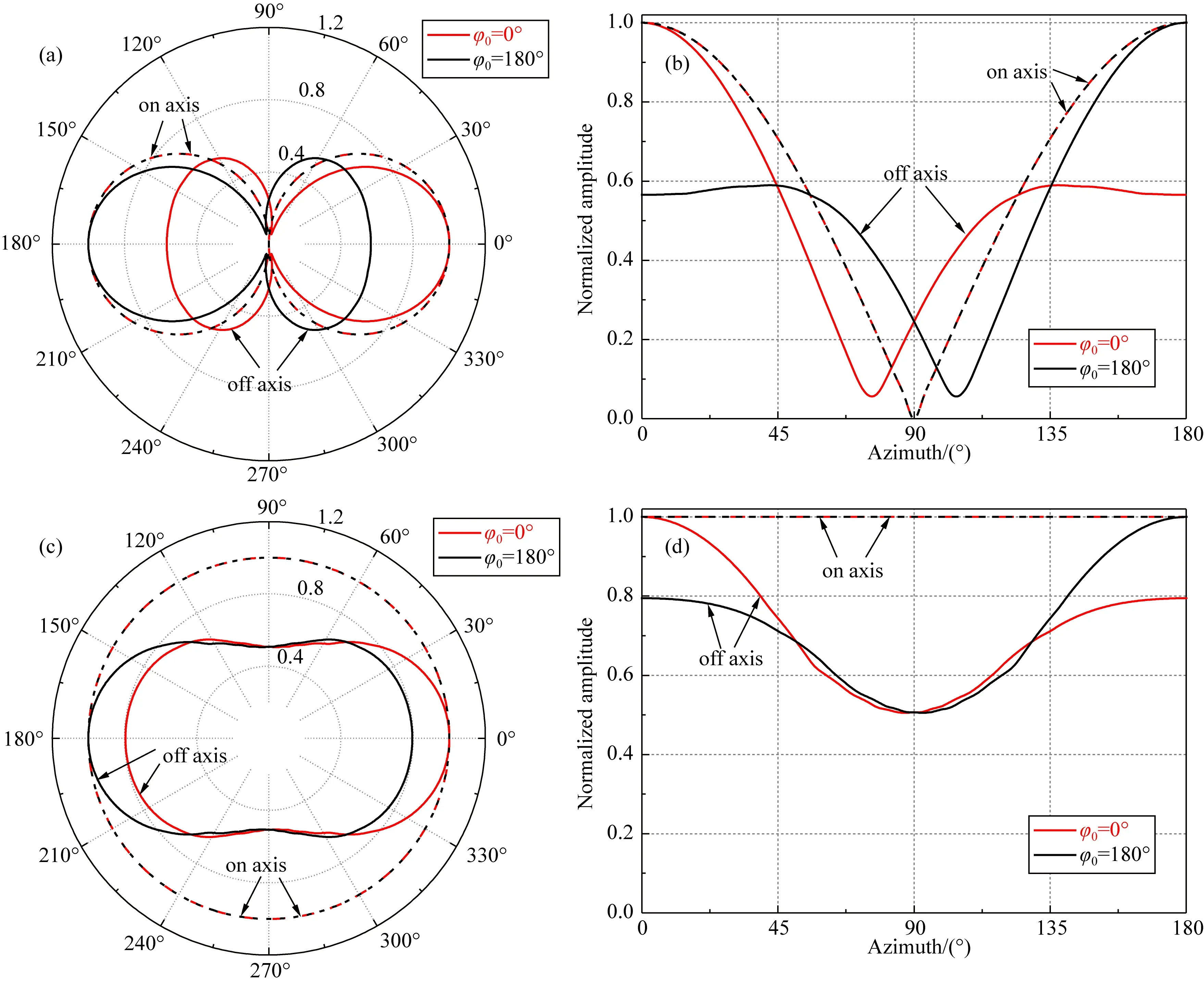
圖5 對于兩個相反方位的反射體，SV橫波入射引起的井內波場的方位響應(a)、(b) 徑向位移； (c)、(d) 聲壓.Fig.5 The azimuthal response of waveforms inside borehole for SV-wave incidence for the 0° (red) and 180° (black) reflector positions. For comparison, the on-axis result (dashed curves) is also plotted(a) and (b) Radial displacement; (c) and (d) Pressure.

接下來我們將重點分析不同接收器偏心距、聲源頻率和地層類型下裸眼及套管井中接收波場的方位響應特征.

3 裸眼和套管井中接收波場方位響應的影響因素研究

3.1 接收器偏心距對井中接收波場的影響

圖6和圖7分別給出了裸眼井、自由套管和套管膠結良好情況下，SH和SV橫波入射時，不同偏心距接收器接收到的井內流體徑向位移和聲壓的方位幅值響應曲線.計算所用聲源的中心頻率為3000 Hz，源距為3 m，反射體傾角為60°，位于0°方位，虛源的徑向距離為30 m，井孔和地層參數見表1(采用地層1).對于0.001 m的微小偏心距，三種情況下SH和SV橫波入射引起的井內流體的徑向位移響應相對于90°方位幾乎對稱，與圖4和圖5中接收器居中接收的結果相似，此時徑向位移的測量結果主要以偶極成分為主，這也說明較小的偏心距對測量結果的影響可以忽略.隨著偏心距離從0.001 m增加到0.05 m，當SH橫波入射時，裸眼井和自由套管情況下井中接收徑向位移和聲壓的振幅最大值所在方位均逐漸偏離反射體位置，而膠結良好套管井中呈現出偏離方位相反的現象；當SV橫波入射時，三種情況下井中接收徑向位移的振幅最小值所在方位均逐漸靠近反射體位置，并且其振幅最小值隨著偏心距的增加而逐漸增大.此外，SV橫波入射時井內聲壓的振幅最大值所在方位不受接收器偏心距的影響，但受井類型的影響，在裸眼井和膠結良好套管井中，靠近反射體一側的接收器接收到的聲壓幅值最大，而在自由套管中則是遠離反射體一側的接收器將接收到最大幅值的聲壓.值得注意的是，雖然加套管之后井中方位接收響應的變化規律不盡相同，但與裸眼井情況相比，自由套管和套管膠結良好時井中接收波場的方位響應受接收器偏心距的影響更大，說明套管井中的波場響應對井外反射體方位的靈敏度更高.

圖6 快速地層條件下，SH橫波入射時，不同偏心距接收器接收到的井內波場的方位響應(a) 裸眼井； (b) 自由套管； (c) 膠結良好.Fig.6 The azimuthal response of waveforms inside borehole received by receivers with different eccentric distances for SH-wave incidence in the fast formation(a) Open hole; (b) Cased hole with free pipe; (c) Cased hole with good bonding.

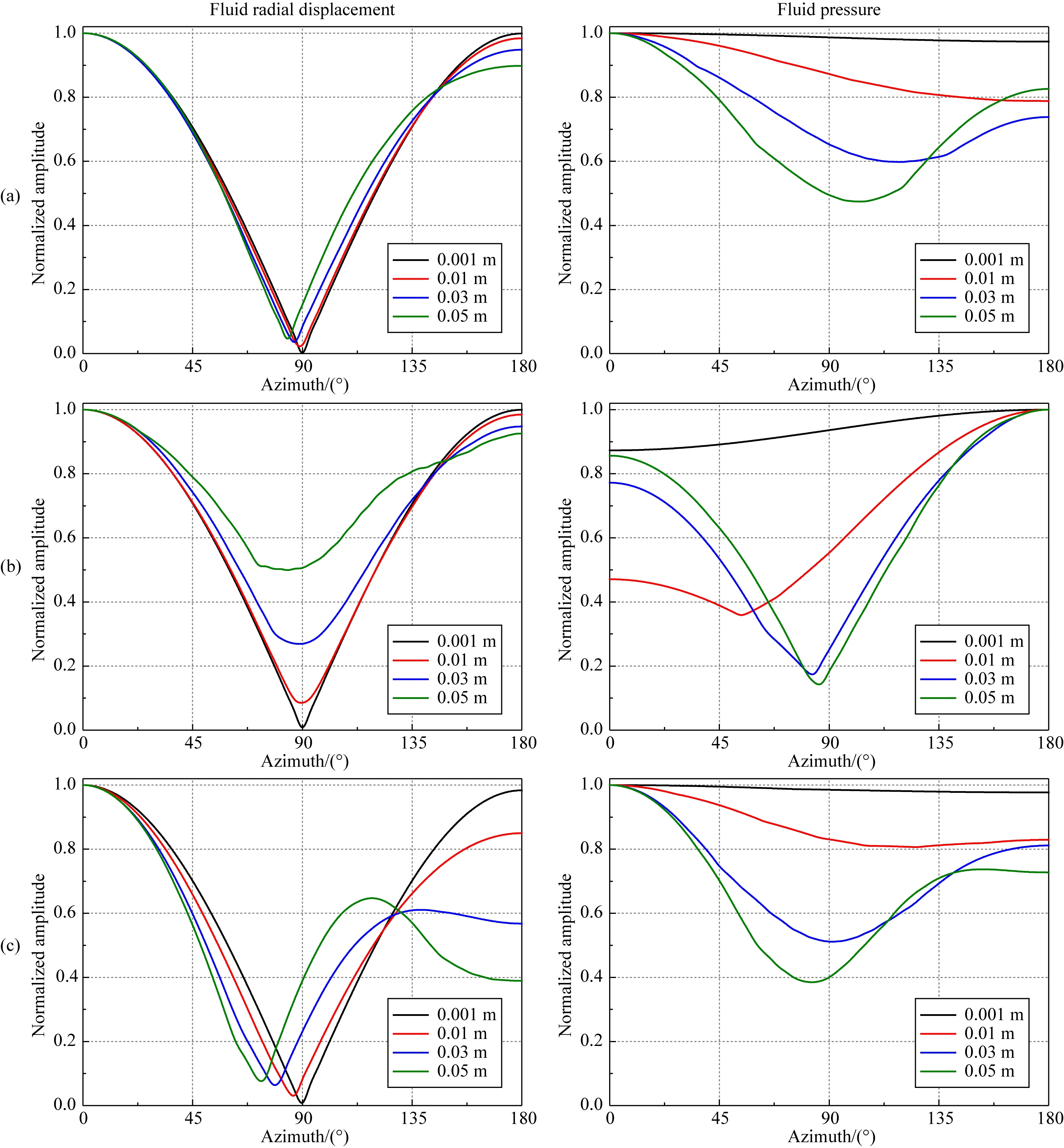
圖7 快速地層條件下，SV橫波入射時，不同偏心距接收器接收到的井內波場的方位響應(a) 裸眼井； (b) 自由套管； (c) 膠結良好.Fig.7 The azimuthal response of waveforms inside borehole received by receivers with different eccentric distances for SV-wave incidence in the fast formation(a) Open hole; (b) Cased hole with free pipe; (c) Cased hole with good bonding.

3.2 聲源頻率對井中接收波場的影響

圖8和圖9是聲源頻率變化時，SH和SV橫波入射到裸眼井、自由套管和膠結良好套管井中引起的井內流體的徑向位移和聲壓的方位幅值響應曲線.計算時接收器的偏心距離為0.035 m，其他參數與圖6中相同.從圖中可看出，對于100 Hz的低頻情況，SH和SV橫波入射引起的井內流體的徑向位移響應相對于90°方位幾乎對稱.這是因為頻率非常低時，聲波波長遠大于井徑，使井孔的調制作用明顯減弱，說明低頻時可忽略接收器的偏心效應.隨著頻率從100 Hz增加到5000 Hz，當SH橫波入射時，自由套管和膠結良好情況下井中接收徑向位移和聲壓的振幅最大值所在方位均先靠近后偏離反射體位置，但在裸眼井情況下則表現出先靠近后偏離再靠近反射體位置的現象.當SV橫波入射時，隨著頻率增加，三種情況下井中接收徑向位移和聲壓的方位響應較為復雜，其幅度最大值所在方位發生了180°反轉.并且某些頻率下，聲壓最大值所在方位既不位于靠近反射體一側，也不位于遠離反射體一側(比如裸眼井在500 Hz和1000 Hz時，以及膠結良好套管井在500 Hz、1000 Hz和2000 Hz時).上述結果表明，雖然聲源頻率能夠顯著改變井內接收波場的方位響應特征，但方位響應隨頻率呈復雜變化.

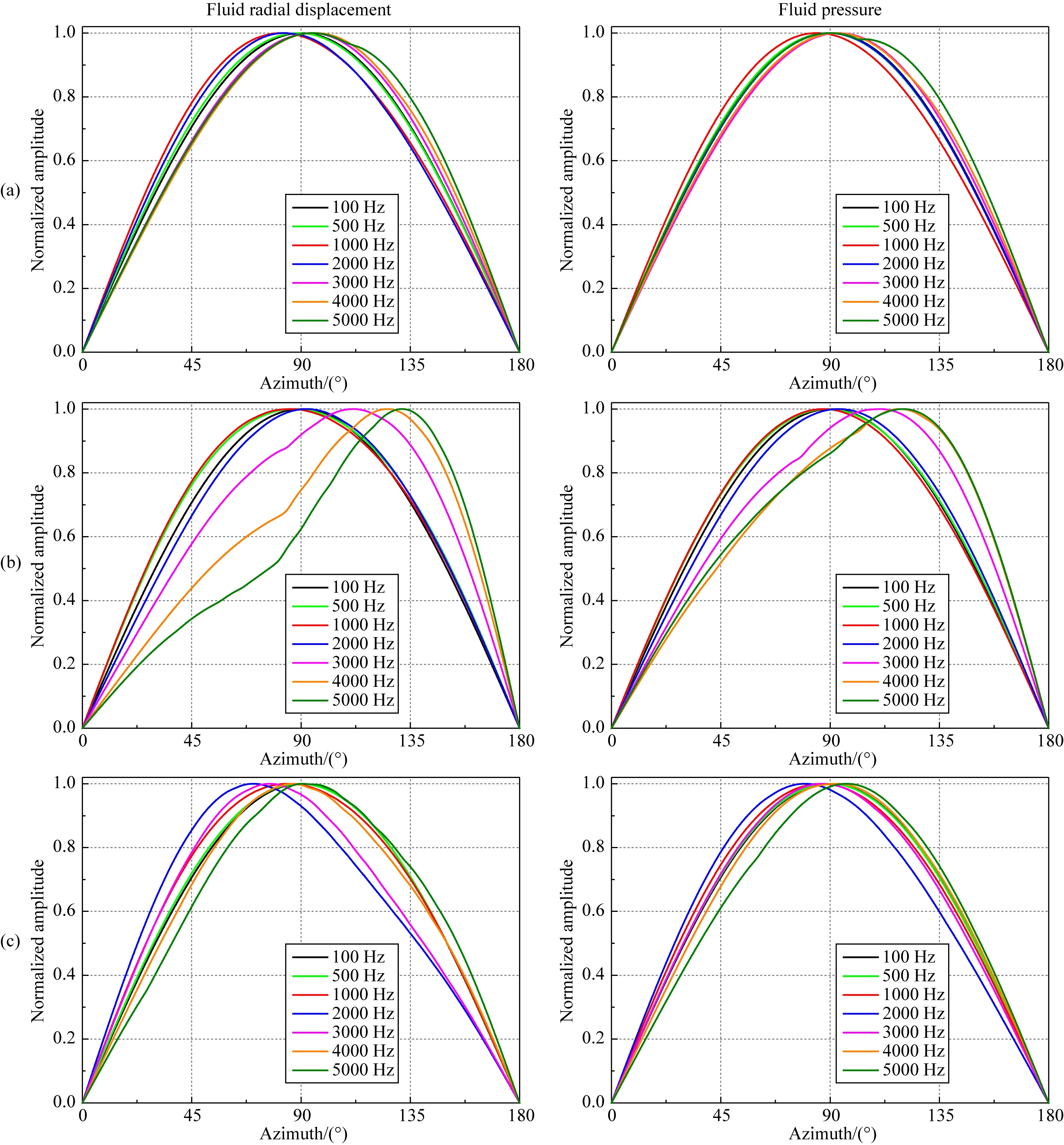
圖8 快速地層條件下，聲源頻率不同時，SH橫波入射引起的井內波場的方位響應(a) 裸眼井； (b) 自由套管； (c) 膠結良好.Fig.8 The azimuthal response of waveforms inside borehole at different frequencies for SH-wave incidence in the fast formation(a) Open hole; (b) Cased hole with free pipe; (c) Cased hole with good bonding.

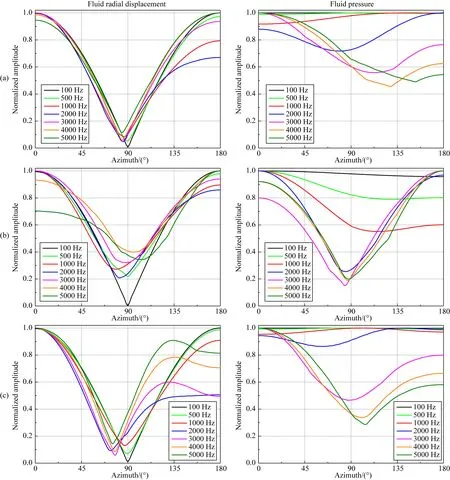
圖9 快速地層條件下，聲源頻率不同時，SV橫波入射引起的井內波場的方位響應(a) 裸眼井； (b) 自由套管； (c) 膠結良好.Fig.9 The azimuthal response of waveforms inside borehole at different frequencies for SV-wave incidence in the fast formation(a) Open hole; (b) Cased hole with free pipe; (c) Cased hole with good bonding.

3.3 地層類型對井中接收波場的影響

除了接收器偏心距和聲源頻率外，地層類型也會影響井中接收波場的方位響應.圖10和圖11對比了快速和慢速地層條件下，SH和SV橫波入射到裸眼井、自由套管和膠結良好套管井中引起的井內流體的徑向位移和聲壓的方位幅值響應.計算時接收器的偏心距為0.035 m，聲源主頻為3000 Hz，其他參數與圖6中相同.從圖10中可以看出，當SH橫波入射時，裸眼井和自由套管井中流體徑向位移和聲壓的振幅最大值所在方位在快速地層條件下均由90°向遠離反射體一側偏移，而在慢速地層中均向靠近反射體一側偏移，呈現出相反的現象；在快速和慢速地層條件下，膠結良好時的結果均由90°向靠近反射體一側偏移.當SV橫波入射時(圖11)，無論在快速還是慢速地層中，三種情況下井中流體徑向位移的振幅最小值所在方位的變化趨勢相同，均由90°向靠近反射體一側偏移，并且靠近反射體的接收器將接收到最大幅值的徑向位移；相對于快速地層，在慢速地層中三種情況下的聲壓方位響應均反生180°反轉.上述分析表明，當根據井內接收波場的幅值信息對井外反射體進行方位識別時，需要考慮地層性質的影響.

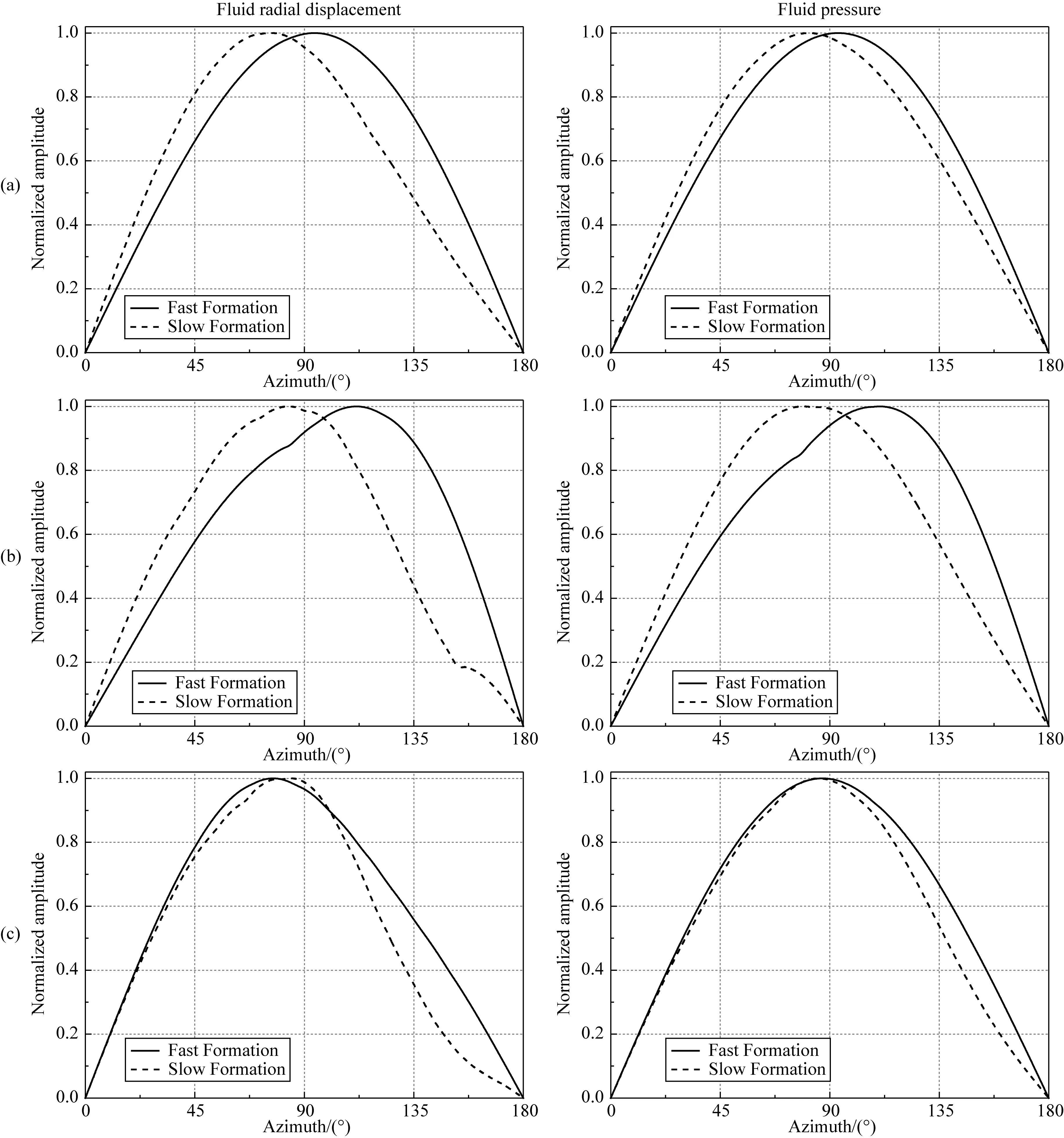
圖10 快速和慢速地層條件下，SH橫波入射引起的井內波場的方位響應(a) 裸眼井； (b) 自由套管； (c) 膠結良好.Fig.10 The azimuthal response of waveforms inside borehole for SH-wave incidence in the fast and slow formations(a) Open hole; (b) Cased hole with free pipe; (c) Cased hole with good bonding.

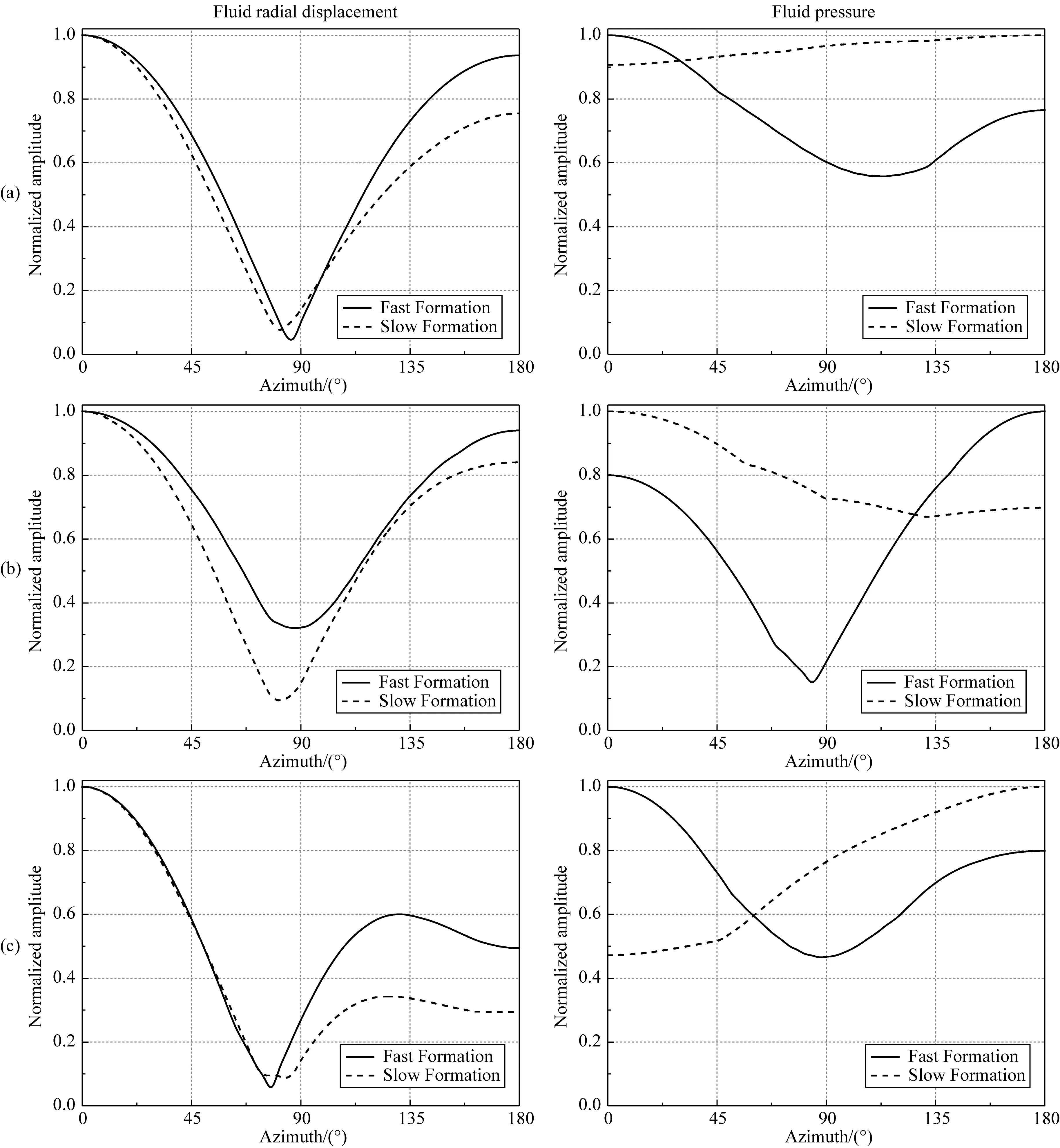
圖11 快速和慢速地層條件下，SV橫波入射引起的井內波場的方位響應(a) 裸眼井； (b) 自由套管； (c) 膠結良好.Fig.11 The azimuthal response of waveforms inside borehole for SV-wave incidence in the fast and slow formations(a) Open hole; (b) Cased hole with free pipe; (c) Cased hole with good bonding.

4 井中聲場方位幅值響應反轉現象的正確性驗證

上一節研究了偶極橫波遠探測在裸眼和套管井中接收波場的方位響應特征，我們注意到對于不同的模型參數，井中接收波場的方位幅值特征存在較大差異，在某些情況下甚至會出現相反的現象，過去文獻中鮮有類似報道.為了證實這一現象，以SV橫波入射到裸眼井中為例，進一步通過三維有限差分法模擬不同頻率下井中接收波場的方位響應特征.差分模擬時聲源上方共有32個接收器等間隔環向布置，其他參數與圖3中相同.考慮聲源頻率為1500 Hz和4000 Hz兩種情況，三維有限差分的計算結果分別如圖12中圓圈和三角形標記所示，其中圖12a、b分別為流體徑向位移和聲壓的方位響應.為了對比，圖中同時給出了利用式(12)得到的解析結果(實線和虛線).從圖中可以看出，無論頻率為1500 Hz還是4000 Hz時，兩種方法計算得到的流體徑向位移和聲壓的方位響應結果均吻合較好.此外，在不同頻率下，兩種方法均顯示出了相反的結果：當頻率為1500 Hz時，靠近(遠離)反射體一側的接收器接收到的徑向位移(聲壓)幅值最大；而當頻率為4000 Hz時，則是遠離(靠近)反射體一側的接收器將接收到最大幅值的徑向位移(聲壓).三維有限差分計算結果證實了方位幅值響應存在180°反轉現象，指示利用井中接收波場幅值特征進行井外反射體方位識別時需要考慮接收器偏心距、聲源頻率和地層性質等因素的影響，這對于儀器研制和現場解釋具有重要的指導意義.

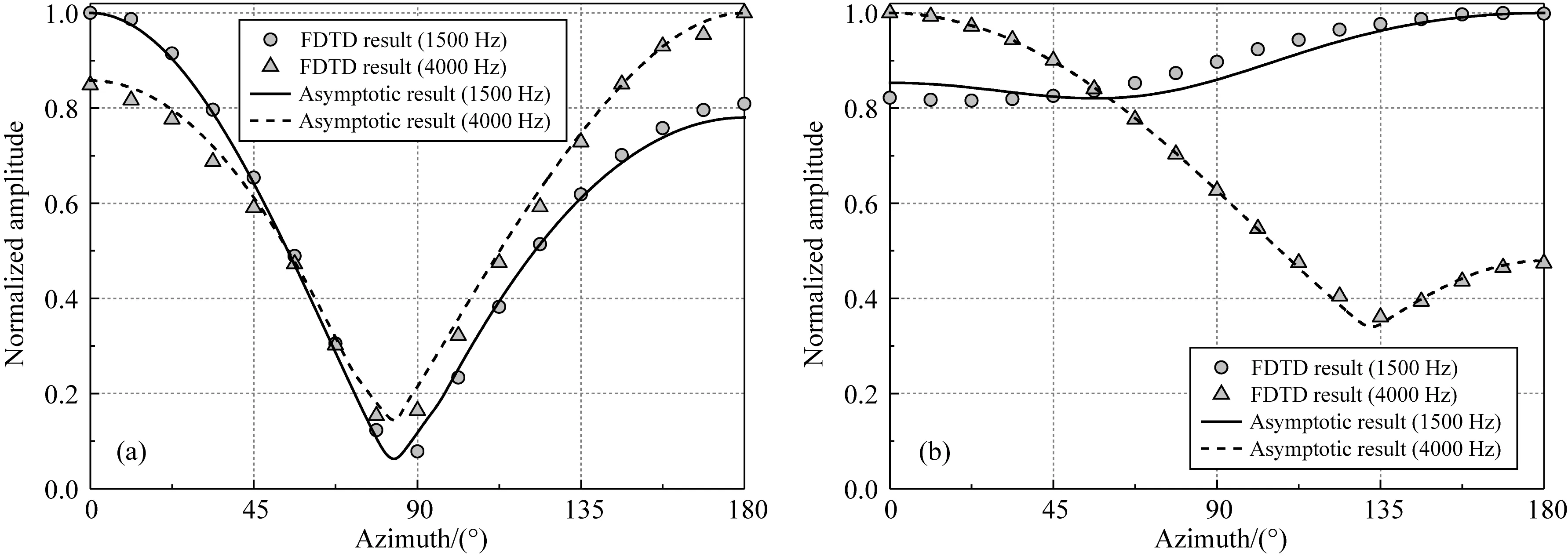
圖12 快速地層條件下，聲源頻率為1500 Hz和4000 Hz時，SV橫波入射引起的井中接收波場的方位響應(a) 徑向位移； (b) 聲壓.為了對比，同時給出了漸近解(曲線)和三維有限差分(標記)的計算結果.Fig.12 The azimuthal response of waveforms inside borehole at frequencies 1500 Hz and 4000 Hz for SV-wave incidence in the fast formation(a) Radial displacement; (b) Pressure. The curves and circles are calculated using analytical (curves) and 3D finite-difference (markers) modeling, respectively.

5 結論

本文采用解析法和三維有限差分法對偶極橫波遠探測在裸眼和套管井中接收波場的方位響應特征進行了研究，得到以下認識和結論：

(1)結合虛源和球面波的柱面波展開，采用最速下降法得到了充液裸眼和套管井中偶極橫波方位遠探測接收波場的漸近解析解.通過解析法和三維有限差分法對套管井中方位接收波場的模擬對比，驗證了漸近解的正確性和普適性.

(2)SH橫波入射引起的井內流體的徑向位移和聲壓的方位響應特征具有較好的一致性，而SV橫波入射時二者特征卻存在較大差異.值得注意的是，SV橫波入射時，井內波場的方位幅值響應對井外反射體位置具有唯一性，即在常用偶極測井頻率下，靠近或遠離反射體的接收器接收到的波形幅值最大.這表明在進行聲波遠探測成像解釋時，考慮井內接收信號中的SV分量有助于識別井外反射體的方位，但需要注意接收換能器記錄的信號類型(徑向位移/聲壓)的不同響應.

(3)偶極橫波遠探測井內接收波場的方位響應特征受井眼環境、接收器偏心距、聲源頻率和地層性質等多個因素的影響，在不同參數下方位幅值響應甚至會出現反轉現象，漸近解析解和三維有限差分數值解的結果對比證實了這一現象，實際數據解釋時需要考慮這些因素的影響.此外，在影響井內聲場方位響應的眾多因素當中，最重要的主控因素是接收器偏心距.正是由于偏心接收才有文中不同于偶極180°對稱性的變化現象(即圖4—圖12所示結果)，其物理實質是聲場在偏離井心位置上的復雜三維變化；而居中時三維變化就降到了二維，復雜性減少但(180°)對稱現象出現.

(4)相對于裸眼井，套管井中接收波場的方位響應對井外反射體位置的靈敏度更高，受接收器偏心距、聲源頻率和地層性質的影響也更大，說明在套管井中進行偶極橫波方位遠探測更有利于井外反射體的方位識別.

(5)現有的偶極橫波測井儀將儀器兩側的接收換能器記錄的信號之差作為測量信號，此時無論換能器記錄的是流體徑向位移還是聲壓，相減后的測量信號中都主要包含偶極成分，可以得到反射體的走向信息；接收器的偏心效應包含了反射體的傾向信息，有助于解決偶極橫波遠探測方位的180°不確定性問題.

附錄A 裸眼井情況下矩陣方程中的元素表達式

矩陣M中各元素的具體表達式為：

M11=-nIn(fa)/a-fIn+1(fa),

M12=nKn(pa)/a-pKn+1(pa),

M13=nKn(sa)/a,

M14=ik[nKn(sa)/a-sKn+1(sa)],

M21=ρfω2In(fa),

M22=2ρβ2[(n2-n)Kn(pa)/a2+pKn+1(pa)/a]

+ρ(2k2β2-ω2)Kn(pa),

M23=2nρβ2[(n-1)Kn(sa)/a2-sKn+1(sa)/a],

M24=2ikρβ2{[(n2-n)/a2+s2]Kn(sa)

+sKn+1(sa)/a},

M31=0,

M32=2nρβ2[(1-n)Kn(pa)/a2+pKn+1(pa)/a],

M33=-ρβ2{[2(n2-n)/a2+s2]Kn(sa)

+2sKn+1(sa)/a},

M34=2iknρβ2[(1-n)Kn(sa)/a2+sKn+1(sa)/a],

M41=0,

M42=2ikρβ2[nKn(pa)/a-pKn+1(pa)],

M43=iknρβ2Kn(sa)/a.

M44=-(s2+k2)ρβ2[nKn(sa)/a-sKn+1(sa)].

(A1)

向量b和b′中的元素由于入射波的類型不同而有所區別.當SH橫波入射時，向量b和b′中各元素的具體表達式為(省略公共因子S(ω)·RDSH(ω)·RFSH(ω))：

b1=-nεnIn(sa)sin(nφ0)/a,

b2=-2nεnρβ2[(n-1)In(sa)/a2

+sIn+1(sa)/a]sin(nφ0),

b3=εnρβ2{[2(n2-n)/a2+s2]In(sa)

-2sIn+1(sa)/a}sin(nφ0),

b4=-iknεnρβ2In(sa)sin(nφ0)/a,

b′1=nεnIn(sa)cos(nφ0)/a,

b′2=2nεnρβ2[(n-1)In(sa)/a2+sIn+1(sa)/a]

×cos(nφ0),

b′3=-εnρβ2{[2(n2-n)/a2+s2]In(sa)

-2sIn+1(sa)/a}cos(nφ0),

b′4=iknεnρβ2In(sa)cos(nφ0)/a.

(A2)

當SV橫波入射時，向量b和b′中各元素的具體表達式為(省略公共因子S(ω)·RDSV(ω)·RFSV(ω))：

b1=-ikεn[nIn(sa)/a+sIn+1(sa)]cos(nφ0),

b2=-2ikεnρβ2{[(n2-n)/a2+s2]In(sa)

-sIn+1(sa)/a}cos(nφ0),

b3=-2iknεnρβ2[(1-n)In(sa)/a2-sIn+1(sa)/a]

×cos(nφ0),

b4=εn(s2+k2)ρβ2[nIn(sa)/a+sIn+1(sa)]cos(nφ0),

b′1=-ikεn[nIn(sa)/a+sIn+1(sa)]sin(nφ0),

b′2=-2ikεnρβ2{[(n2-n)/a2+s2]In(sa)

-sIn+1(sa)/a}sin(nφ0),

b′3=-2iknεnρβ2[(1-n)In(sa)/a2

-sIn+1(sa)/a]sin(nφ0),

b′4=εn(s2+k2)ρβ2[nIn(sa)/a+sIn+1(sa)]sin(nφ0)，

(A3)

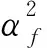
附錄B 套管井(膠結良好)情況下T矩陣的元素表達式

T矩陣的元素表達式為：

T11=nIn(pR)/R+pIn+1(pR),

T12=nKn(pR)/R-pKn+1(pR),

T13=nIn(sR)/R,

T14=nKn(sR)/R,

T15=ik[nIn(sR)/R+sIn+1(sR)],

T16=ik[nKn(sR)/R-sKn+1(sR)],

T21=-nIn(pR)/R,

T22=-nKn(pR)/R,

T23=-nIn(sR)/R-sIn+1(sR),

T24=-nKn(sR)/R+sKn+1(sR),

T25=-iknIn(sR)/R,

T26=-iknKn(sR)/R,

T31=ikIn(pR),

T32=ikKn(pR),

T33=0,

T34=0,

T35=-s2In(sR),

T36=-s2Kn(sR),

T41=2ρβ2[(n2-n)In(pR)/R2-pIn+1(pR)/R]

+ρ(2k2β2-ω2)In(pR),

T42=2ρβ2[(n2-n)Kn(pR)/R2+pKn+1(pR)/R]

+ρ(2k2β2-ω2)Kn(pR),

T43=2nρβ2[(n-1)In(sR)/R2+sIn+1(sR)/R],

T44=2nρβ2[(n-1)Kn(sR)/R2-sKn+1(sR)/R],

T45=2ikρβ2{[(n2-n)/R2+s2]In(sR)

-sIn+1(sR)/R},

T46=2ikρβ2{[(n2-n)/R2+s2]Kn(sR)

+sKn+1(sR)/R},

T51=2nρβ2[(1-n)In(pR)/R2-pIn+1(pR)/R],

T52=2nρβ2[(1-n)Kn(pR)/R2+pKn+1(pR)/R],

T53=-ρβ2{[2(n2-n)/R2+s2]In(sR)

-2sIn+1(sR)/R},

T54=-ρβ2{[2(n2-n)/R2+s2]Kn(sR)

+2sKn+1(sR)/R},

T55=2iknρβ2[(1-n)In(sR)/R2-sIn+1(sR)/R],

T56=2iknρβ2[(1-n)Kn(sR)/R2+sKn+1(sR)/R],

T61=2ikρβ2[nIn(pR)/R+pIn+1(pR)],

T62=2ikρβ2[nKn(pR)/R-pKn+1(pR)],

T63=iknρβ2In(sR)/R,

T64=iknρβ2Kn(sR)/R,

T65=-(s2+k2)ρβ2[nIn(sR)/R+sIn+1(sR)],

T66=-(s2+k2)ρβ2[nKn(sR)/R-sKn+1(sR)].

(B1)

附錄C 套管井(自由套管)情況下矩陣方程中的元素表達式

矩陣H中各元素的具體表達式為(未列出的元素取值為0)：

H11=-nIn(fr1)/r1-fIn+1(fr1),

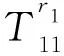
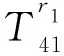
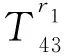
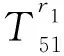
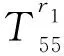
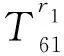
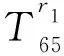
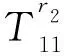
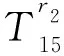
H58=-nIn(fr2)/r2-fIn+1(fr2),

H59=-nKn(fr2)/r2+fKn+1(fr2),

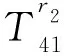
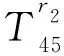
H69=ρfω2Kn(fr2),

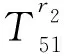
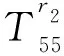
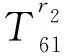
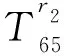
H98=-nIn(fa)/a-fIn+1(fa),

H99=-nKn(fa)/a+fKn+1(fa),

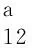
H10,8=ρfω2In(fa),H10，9=ρfω2Kn(fa),

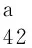
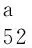
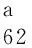
(C1)

其中，r1和r2分別為套管的內半徑和外半徑；T的右上標表示計算時半徑R的取值.

根據入射波類型的不同(即SH或SV橫波入射)，向量d和d′中的元素也有所區別，其各元素的具體表達式為(未列出的元素取值為0)：

d9=b1,d10=b2,d11=b3,d12=b4,

d′9=b′1,d′10=b′2,d′11=b′3,d′12=b′4.

(C2)

附錄D 井軸處的聲壓和徑向位移

首先求解井軸處的聲壓，第一類變型貝塞爾函數具有如下性質：

(D1)

其中，n為階數.接收器位于井軸時，式(12)中的r=0，由式(D1)可知，此時聲壓的多極響應中只有n=0這一項有值，其余全為0，表達式為：

(D2)

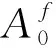
求解井軸處的徑向位移時，需要用到第一類變型貝塞爾函數的遞推公式：

(D3)

其中，x為變量.將式(D3)代入式(12)的徑向位移表達式中可得：

×[In-1(f0r)+In+1(f0r)].

(D4)

n=0時，式(D4)中將出現負數階貝塞爾函數，可根據整階貝塞爾函數的奇偶性進行計算，公式為：

I-n(x)=In(x).

(D5)

令式(D4)中的r=0，將式(D1)和(D5)代入式(D4)中，得到井軸處的徑向位移為：

(D6)

式(D6)表明，井軸處的徑向位移只有偶極項(n=1)貢獻.