基于RBFNN-GA的縱封熱封過程工藝參數決策方法研究

彭來湖，徐欽棟

(1.浙江理工大學，浙江 杭州 310000；2.浙江理工大學龍港研究院，浙江 溫州 325000)

1 引言(Introduction)

隨著包裝行業的快速發展，對軟包加工機械設備的智能化要求越來越高，其中枕式包裝機在包裝裝備中發展最早，應用最廣。雖然我國枕式包裝機設備研發能力有了一定程度的發展，許多高校與研發機構也紛紛參與包裝機械的研發工作，但是枕式包裝機縱封熱封加工過程依舊存在智能化不足、工藝參數選擇效率低等問題。

對于縱封熱封過程工藝參數的選擇問題，國內外學者都對其進行了研究。AIYENGAR等與曹菲等在實驗室條件下對三種類型的復合膜進行熱封強度的測定，同時分析不同失效模式，通過不同的失效模式對數據進行分類，得出了簡單的定性關系，但該方法缺少定量關系，難以應用到實際生產過程當中；杜玉寶在對復合膜進行熱封強度測試后，通過數據進行二次多項式回歸擬合，得出了工藝參數與熱封強度的關系曲線，但應用到實際生產加工還需將實驗工藝參數轉換成實際工程參數。已有的研究工作缺少了實際生產的分析，同時未對熱封強度多參數的情況尋找其最優解。

本文以熱封強度作為生產質量的重要判定依據，并且考慮包裝機在工作工程中受到復雜工藝的影響，進行枕式包裝機工藝參數決策方法研究。首先對加工流程中的各個生產數據進行統計，其次通過RBF神經網絡進行回歸模型的訓練，然后根據復合膜材料斷裂屈服強度確定目標熱封強度，最后通過遺傳算法，迭代尋找最優結果。

2 包裝機工藝分析(Process analysis of the packaging machine)

2.1 包裝機熱封流程

枕式包裝機縱封結構，采用雙平板熱封結構，如圖1所示，結構1、3為復合膜旋轉擠壓輥，通過主動旋轉帶動復合膜向前運動，同時會對復合膜產生相對恒定的壓力；結構2為雙板導熱機構，以電生熱方式控制雙板間的溫度達到設定溫度。復合膜在結構1前旋轉擠壓輥的帶動下向前運動，同時使復合膜內膜緊貼；結構2的雙板之間存在一定的間隙，距離為，復合膜通過該間隙時高溫使其預熱融化；結構3后旋轉擠壓輥對預熱后的復合膜內膜進行擠壓貼合，達到熱封效果，最后采用QBT 2358-1998標準進行熱封強度的測定，單位為N/15mm。根據熱封強度對熱封效果進行判定。

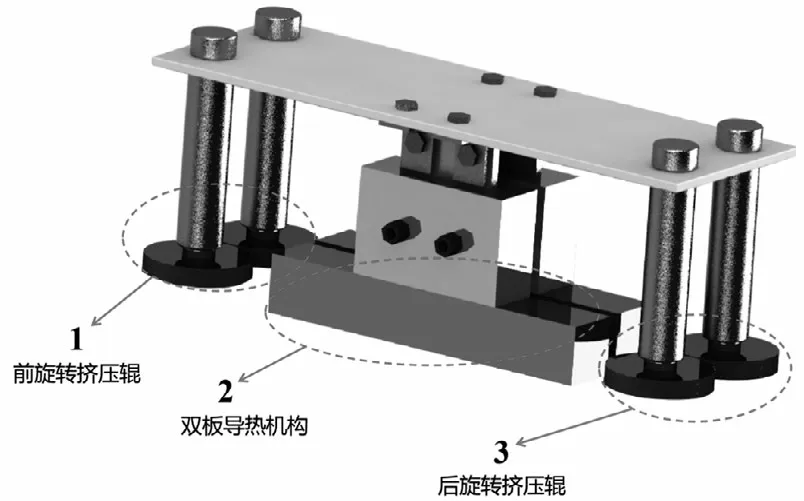
圖1 縱封熱封機構Fig.1 Structure of longitudinal and heat sealing machine

在熱封過程中，熱封時間為縱封熱封過程當中的重要影響因素，但在實際生產加工過程當中無法對熱封時間進行精確設定。本文針對枕式包裝機實際加工流程，通過熱封速度來代替表示熱封時間。熱封速度的單位為包/min，與熱封時間的關系如式(1)所示。

其中，為加熱板長度，單位為mm，為復合膜長度，單位為mm。綜上所述，在實際機床加工過程當中，對熱封強度的主要影響因素包括雙平板熱封距離、熱封溫度和熱封速度。

2.2 熱封效果分析

枕式包裝機產品的熱封強度是對熱封效果的一個重要判定因素，通常是測量復合膜材料熱封處的力學性能進行判定。對復合膜材料進行熱封處理后，對其進行縱向實驗拉伸會產生四種不同情況。

如圖2(a)所示為熱封后復合膜狀態，1處為熱封層層間結合處，2為復合膜層間結合處；如圖2(b)所示為復合膜內層斷裂狀態，當熱封強度與復合膜層間結合強度相差較小時，復合膜層間發生斷裂分離，此時熱封效果較好；如圖2(c)所示為熱封失效狀態，熱封強度較低，復合膜層間結合強度遠大于熱封強度，此狀態熱封效果最差；如圖2(d)所示為整體撕裂狀態，當熱封強度大于復合膜材料的斷裂屈服強度時發生整體撕裂，此時雖然熱封強度較大，但熱封表面發生扭曲變形，其韌性與外觀表面都無法達到要求，熱封效果較差。綜上所述，熱封強度可以極大地反映出復合膜材料的熱封效果。

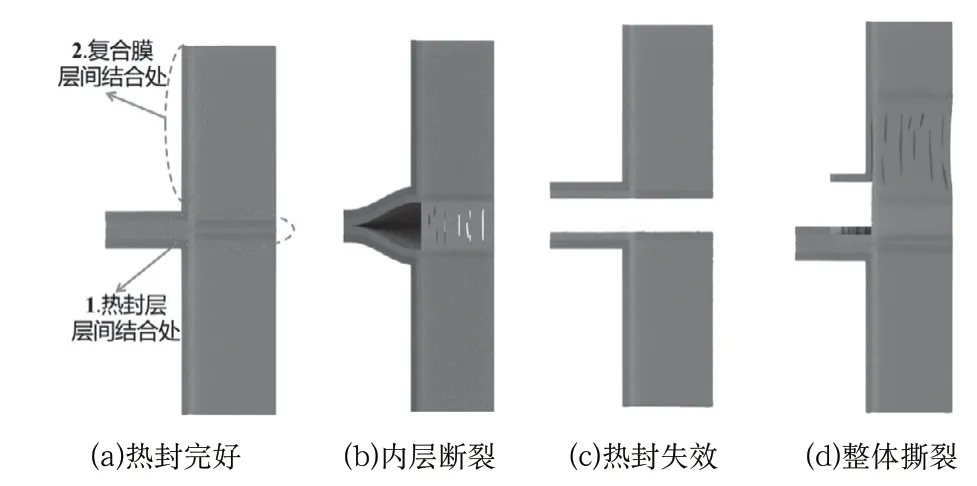
圖2 熱封狀態示意圖Fig.2 Schematic diagram of heat sealing state

根據實際生產過程統計可知，合適的目標熱封強度P與復合膜自身斷裂的屈服強度P有關。經過實際加工結果統計估算，存在式(2)關系。當熱封強度P滿足式(2)關系，則認為其滿足實際加工需求的熱封強度。

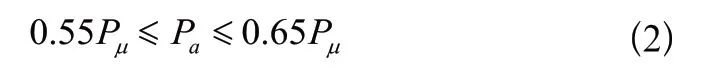
3 RBFNN-GA決策方法(RBFNN-GA decisionmaking method)

3.1 RBFNN-GA決策方法總體結構

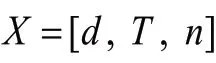
決策方法模型設計結構圖如圖3所示，輸入材料屈服強度計算目標熱封強度，同時根據實際加工需求設定部分工藝參數作為約束條件；建立RBF神經網絡回歸模型并驗證其準確性；將遺傳算法迭代種群輸入到回歸模型中進行適應度計算；通過遺傳算法進行尋優計算，得到熱封強度與目標熱封強度相近的最優工藝參數。

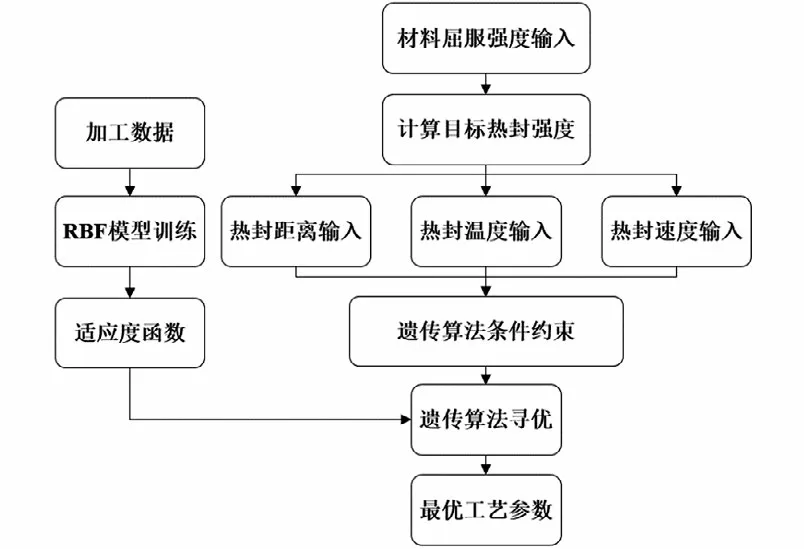
圖3 決策方法結構圖Fig.3 Structure diagram of decision-making method

3.2 RBF神經網絡模型建立

在該決策方法中，對于熱封材料的更換需要進行數據的重新迭代學習，在實際應用過程當中要求該網絡具有較快的收斂性。對于RBF神經網絡，只存在少數幾個連接權值影響輸出，具有較快的收斂性。

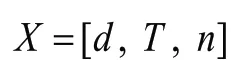
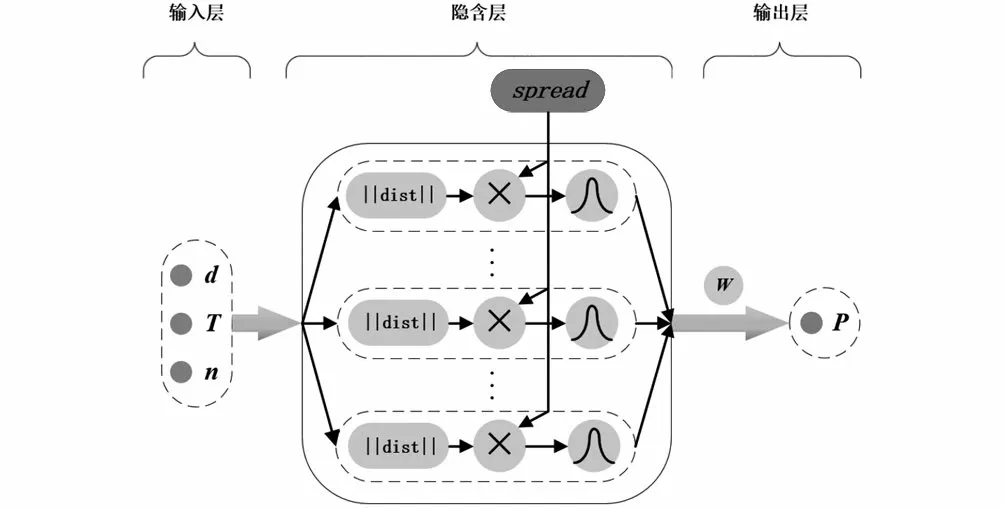
圖4 RBF神經網絡拓撲圖Fig.4 RBF neural network topology

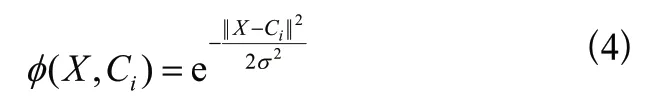
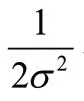
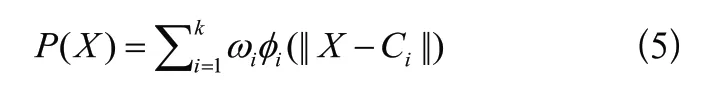
通過式(5)可知，RBF神經網絡就是將每個數據從一個3 維非線性空間轉換到一個維線性可分的空間，即對于組數據的輸入X=(，，???，)與輸出P=(，，???，P)存在式(6)所示關系。

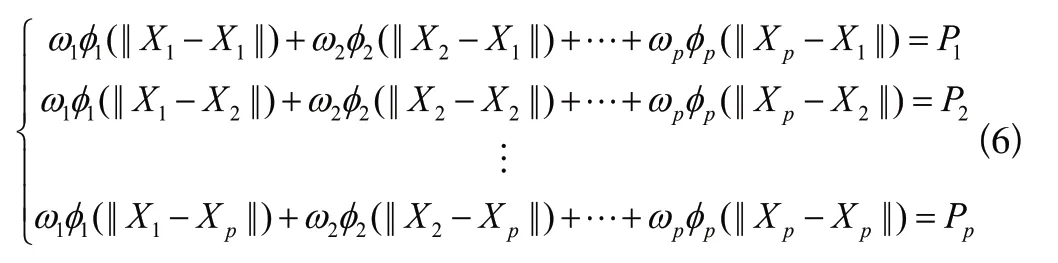
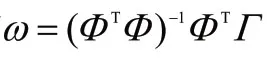
3.3 基于遺傳算法的目標選擇

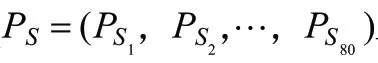
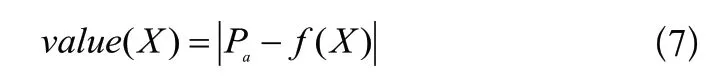
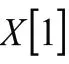
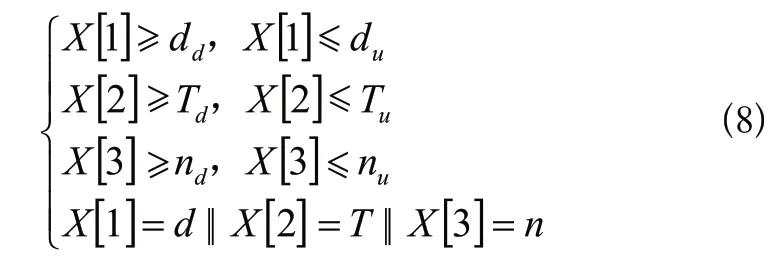
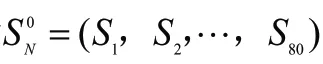
采用合適的選擇算子與交叉算子，可以讓遺傳算法在解決高維非線性問題時，具有很好的魯棒性，避免迭代過程發散；同時采用變異算子，可以使其通過種群間的變異來避免陷入局部最優解。確定遺傳算法算子如下：選擇算子采用輪盤選擇；交叉算子采用點交叉；變異算子采用反轉突變。在遺傳算法迭代前，需要對初始種群進行編碼以提高計算效率，本文采用格雷碼編碼，該編碼方式對于選擇交叉變異等算子具有更快速的計算能力，同時格雷碼變化反映到實數上的變化為連續性，加快了迭代速度。

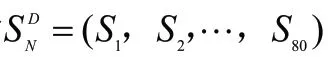
4 模型訓練與試驗驗證(Model training and experimental verification)

4.1 模型訓練

將500 組加工數據采取歸一化處理，并分為400 組訓練集與100 組測試集輸入到RBF神經網絡。設定網絡參數如下：均方差目標為0.001，拓展系數為0.21。將訓練集數據輸入到網絡模型進行訓練，得到的迭代曲線如圖5所示。

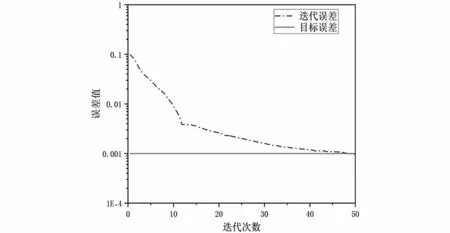
圖5 網絡學習迭代過程Fig.5 Iterative process of network learning

根據曲線變化，在第12 次迭代時，迭代誤差為達到0.003，在第12 次迭代至第50 次迭代過程中，迭代誤差變化相對較小。綜上所述，第12 次迭代至第50 次迭代收益較小，在實際工程應用當中，對于誤差要求較小的情況下，可選取12 次左右的迭代作為網絡學習的結果。

將測試集數據與預測集數據進行對比，結果如圖6所示，從預測值的結果來看，RBF神經網絡模型的整體誤差較小。在熱封強度處于0到25時，預測集與測試集誤差較大，但對于實際加工過程，為保證熱封質量，不會選取該范圍內的熱封強度；在熱封強度處于100到275時，預測集與測試集最大誤差不超過5%，足以滿足實際加工需求。為測試集與預測值進行直觀的數據對比，采用式(9)計算其決定系數。

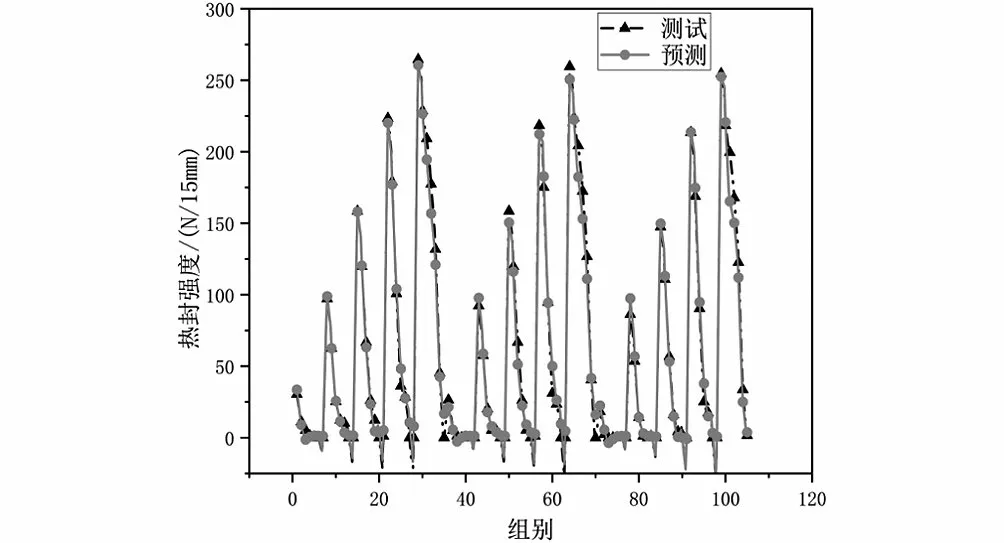
圖6 預測結果對比Fig.6 Comparison of prediction results

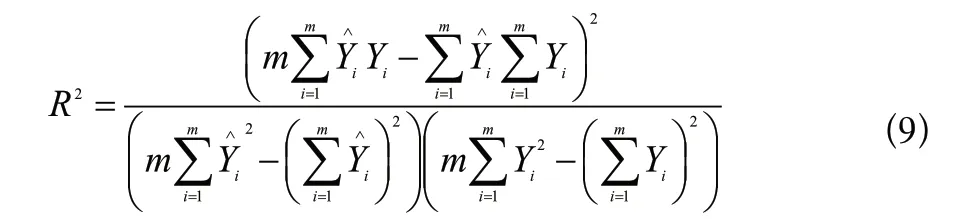
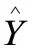
4.2 最優參數尋找

輸入材料的屈服強度為267.65 N/15mm，根據式(3)取目標熱封強度為160 N/15mm，設定三組實驗：第一組實驗設定熱封距離為6 mm，第二組實驗設定熱封溫度為180 ℃，第三組實驗設定熱封速度為80 包/min，同時迭代要求對于最優種群的熱封強度均與目標熱封強度誤差小于5%，以種群平均適應度值為指標，迭代過程如圖7所示，上述三組尋優迭代過程分別如圖7(a)、圖7(b)、圖7(c)所示。

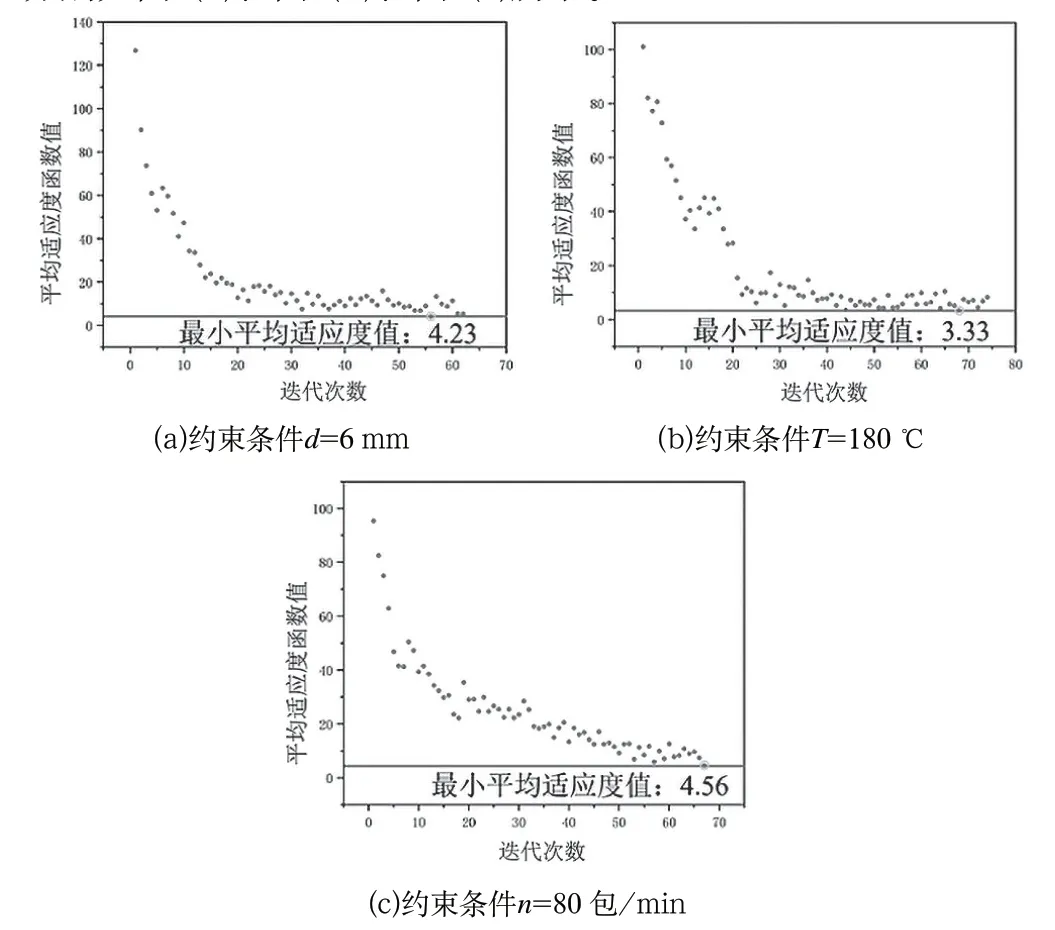
圖7 參數尋優迭代過程Fig.7 Iterative process of parameter optimization

對于三種不同的熱封強度，在迭代次數第10 次到第20 次時，平均適應度值快速下降，迭代次數20 次之后平均適應度值逐漸平穩，在迭代次數大概為70時結束，并且最終迭代結果收斂。對于不同的輸入熱封強度，都可以達到較好的結果，同時誤差滿足加工要求。

4.3 試驗驗證

每組隨機選取最終尋優結果中誤差最小的三組數據，得到如表1所示，在材料的屈服強度為267.65 N/15mm的情況下，3 組不同輸入參數的決策最優解。

表1 最優參數尋優結果Tab.1 Optimization results of optimal parameters

將上述得到的最優工藝參數代入枕式包裝機中生產加工，排除工況意外的產品，從各個情況中隨機選取20 個加工產品進行熱封強度測試，實驗平臺如圖8所示。

圖8 實驗平臺Fig.8 Experimental platform

將表1參數輸入到枕式包裝機中加工，再通過WDW-5型微機控制電子拉力試驗機對加工產品進行熱封強度測試，實驗結果如圖9所示，圖9(a)、圖9(b)、圖9(c)分別為=[6,175,67]、=[7,180,73]和=[5,183,80]條件下，20 個產品熱封強度分布圖。

圖9 產品加工驗證結果圖Fig.9 Result diagram of product processing verification

根據式(2)得出熱封強度上下限范圍，且圖9中三組實驗中抽取的每個加工產品都處于該范圍，證明該方法得出的優化工藝參數在實際工程中有較高的合格率。

5 結論(Conclusion)

為實現對枕式包裝機預先參數輸入來提高加工效率，降低人力成本，構建了基于RBFNN-GA的工藝參數決策方法。

從實驗數據中得出了不同工藝參數與熱封強度的非線性關系，采取RBF神經網絡對熱封強度進行預測。通過數據集對比可知，基于RBF神經網絡構建的回歸模型具有較高的準確性與較快的收斂性，模型有效部分總體誤差小于5%，因此該模型可以有效預測熱封強度。

通過輸入不同的參數，以RBF神經網絡為基礎設計適應度函數，再用遺傳算法對最優工藝參數進行選擇，最后得出最優的工藝參數。將最終結果帶入到實際加工過程當中并且測定結果，20 組產品均處于加工要求范圍內，滿足加工需求。

本文提出的決策方法代替人工參數選擇，有效地降低了人力成本，提高了決策效率；對于枕式包裝機的智能化升級提供了理論依據。