賞析考題 變式探究

江蘇省張家港市沙洲中學(xué)（215600）許秋峰

每年的高考真題都具有一定的典型性和創(chuàng)新性，認(rèn)真研究高考真題的命題來源、一題多解、變式探究、引申推廣等非常重要。教師不僅要讓學(xué)生會(huì)做高考真題，還要引導(dǎo)學(xué)生賞析高考題的設(shè)計(jì)精妙之處，感悟命題者的獨(dú)具匠心。對(duì)高考題進(jìn)行變式探究，可拓寬學(xué)生的解題思維，提高學(xué)生的綜合運(yùn)用能力，提升學(xué)生的數(shù)學(xué)學(xué)科核心素養(yǎng)。

一、考題賞析

（2021 年高考數(shù)學(xué)新課標(biāo)Ⅰ卷第15 題）函數(shù)f(x)=|2x-1|-2 lnx的最小值為___________。

綜上，必有f(x) ≥1，當(dāng)且僅當(dāng)x=1 時(shí)不等式取等號(hào)，故所求函數(shù)f(x)的最小值為1。

優(yōu)解：（放縮法）根據(jù)對(duì)數(shù)函數(shù)切線不等式lnx≤x-1（當(dāng)且僅當(dāng)x=1 時(shí)不等式取等號(hào)），可得-2 lnx≥2 -2x（當(dāng)且僅當(dāng)x=1時(shí)不等式取等號(hào)）。

又因?yàn)閨2x-1|≥2x-1（當(dāng)且僅當(dāng)2x-1≥0時(shí)不等式取等號(hào)），所以將這兩個(gè)同向不等式相加可得|2x-1|-2 lnx≥2x-1+2 -2x=1，即f(x) ≥1，當(dāng)且僅當(dāng)即x=1 時(shí)不等式取等號(hào)，故所求函數(shù)f(x)的最小值為1。

解題反思：當(dāng)函數(shù)解析式涉及絕對(duì)值時(shí)，一般需要先去掉絕對(duì)值符號(hào)，再通過分析、利用函數(shù)的單調(diào)性，從而求出函數(shù)的最值，據(jù)此極易想到上述通解。

求解函數(shù)的最值時(shí)，若解析式涉及自然對(duì)數(shù)lnx，可考慮對(duì)數(shù)函數(shù)切線不等式lnx≤x-1（當(dāng)且僅當(dāng)x=1 時(shí)不等式取等號(hào)）在解題中的靈活運(yùn)用，據(jù)此可獲得上述優(yōu)解。

整體來看，本題設(shè)計(jì)較好，具有創(chuàng)新之意——構(gòu)造函數(shù)解析式時(shí)，有意將熟悉的絕對(duì)值函數(shù)與對(duì)數(shù)函數(shù)綜合在一起，體現(xiàn)了新高考考試大綱的理念，即在知識(shí)點(diǎn)交匯處命題，著重考查考生分析問題和解決問題的能力以及綜合運(yùn)用能力。

二、變式探究

常用的切線不等式有以下四個(gè)：①lnx≤x-1（當(dāng)且僅當(dāng)x=1 時(shí)不等式取等號(hào)）；②lnx≤當(dāng)且僅當(dāng)x=e 時(shí)不等式取等號(hào)）；③ex≥x+1（當(dāng)且僅當(dāng)x=0 時(shí)不等式取等號(hào)）；④ex≥ex（當(dāng)且僅當(dāng)x=1 時(shí)不等式取等號(hào)）。可結(jié)合如下圖像（如圖1和圖2）進(jìn)行形象理解和準(zhǔn)確記憶。

圖1

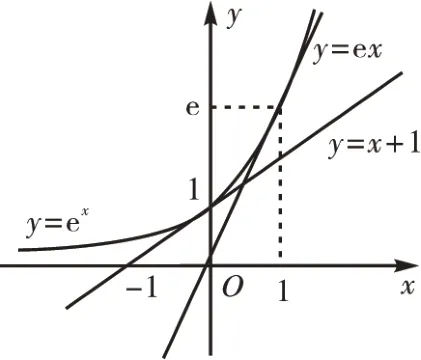
圖2

需要關(guān)注兩點(diǎn)：一是最基本的絕對(duì)值放縮：|x|≥x（當(dāng)且僅當(dāng)x≥0 時(shí)不等式取等號(hào)），|x|≥-x（當(dāng)且僅當(dāng)x≤0 時(shí)不等式取等號(hào)）；二是根據(jù)“同向不等式可相加”這一理論求解最值時(shí)，必須具體分析不等式中的“等號(hào)”能否真正取到。

結(jié)合上述理論知識(shí)，參考2021 年高考數(shù)學(xué)新課標(biāo)Ⅰ卷第15題，可靈活設(shè)計(jì)如下變式題。

變式1：函數(shù)f(x)=|x-2|-e lnx的最小值為__________。

解法一（分類討論法）：當(dāng)x≥2 時(shí)，因?yàn)閒(x)=x-2 -e lnx，所以f′(x)=從而可知：當(dāng)x＞e 時(shí)，f′(x) ＞0；當(dāng)2 ≤x＜e 時(shí)，f′(x) ＜0。于是，函數(shù)f(x)在[)2,e 上單調(diào)遞減，在(e,+∞)上單調(diào)遞增。

當(dāng)0 ＜x＜2 時(shí)，因?yàn)閒(x)=2 -x-e lnx，所以f′(x)=故函數(shù)f(x)在(0,2)上單調(diào)遞減。

又注意到函數(shù)f(x)的圖像在x=2 處連續(xù)，所以可知：函數(shù)f(x)在(0,e)上單調(diào)遞減，在(e,+∞)上單調(diào)遞增，故所求函數(shù)f(x)的最小值為f(e)=-2。

解法二（放縮法）：根據(jù)對(duì)數(shù)函數(shù)切線不等式lnx≤x-1,lnx≤（當(dāng)且僅當(dāng)x=e時(shí)不等式取等號(hào)），可得-e lnx≥-x（當(dāng)且僅當(dāng)x=e時(shí)不等式取等號(hào)）。

又因?yàn)閨x-2|≥x-2（當(dāng)且僅當(dāng)x-2 ≥0 時(shí)不等式取等號(hào)），所以將這兩個(gè)同向不等式相加可得||x-2 -e lnx≥x-2 -x=-2，即f(x) ≥-2，當(dāng) 且僅當(dāng)即x=e 時(shí)不等式取等號(hào)，故所求函數(shù)f(x)的最小值為-2。

變式2：函數(shù)f(x)=|2x+1|-2 ln(1 +x) 的最小值為________。

又注意到函數(shù)f(x)的圖像在x=處連續(xù)，所以可知：函數(shù)f(x)在(-1,0)上單調(diào)遞減，在(0,+∞)上單調(diào)遞增，故所求函數(shù)f(x)的最小值為f(0)=1。

解法二（放縮法）：由對(duì)數(shù)函數(shù)切線不等式得ln(1 +x) ≤(1 +x) -1，即ln(1 +x) ≤x（當(dāng)且僅當(dāng)x=0 時(shí)不等式取等號(hào)），所以-2 ln(1 +x) ≥-2x（當(dāng)且僅當(dāng)x=0時(shí)不等式取等號(hào)）。

又因?yàn)閨2x+1|≥2x+1（當(dāng)且僅當(dāng)2x+1 ≥0時(shí)不等式取等號(hào)），所以將這兩個(gè)同向不等式相加可得|2x+1|-2 ln(1 +x) ≥2x+1 -2x=1，即f(x) ≥1，當(dāng)且僅當(dāng)即x=0 時(shí)不等式取等號(hào)，故所求函數(shù)f(x)的最小值為1。

變式3：函數(shù)f(x)=|2x-1|+2ex的最小值為_______。

又注意到函數(shù)f(x)的圖像在x=處連續(xù)，所以可知：函數(shù)f(x) 在(-∞,0) 上單調(diào)遞減，在(0,+∞)上單調(diào)遞增，故所求函數(shù)f(x)的最小值為f(0)=3。

解法二（放縮法）：根據(jù)指數(shù)函數(shù)切線不等式ex≥x+1（當(dāng)且僅當(dāng)x=0 時(shí)不等式取等號(hào)），可得2ex≥2x+2（當(dāng)且僅當(dāng)x=0時(shí)不等式取等號(hào)）。

又因?yàn)閨2x-1|≥1 -2x（當(dāng)且僅當(dāng)2x-1 ≤0時(shí)不等式取等號(hào)），所以將這兩個(gè)同向不等式相加可得|2x-1|+2ex≥1-2x+2x+2=3，即f(x) ≥3，當(dāng)且僅當(dāng)即x=0 時(shí)不等式取等號(hào)，故所求函數(shù)f(x)的最小值是3。

變式4：函數(shù)f(x)=|x-2 |+ex-1的最小值為________。

解法一（分類討論法）：當(dāng)x≥2 時(shí)，因?yàn)閒(x)=x-2+ex-1，所以f′(x)=1+ex-1＞0，所以函數(shù)f(x)在[2,+∞)上單調(diào)遞增。

當(dāng)x＜2 時(shí)，因?yàn)閒(x)=2 -x+ex-1，所以f′(x)=-1+ex-1，從而可知：當(dāng)1 ＜x＜2 時(shí)，f′(x) ＞0；當(dāng)x＜1時(shí)，f′(x) ＜0。于是，函數(shù)f(x)在(-∞,1)上單調(diào)遞減，在(1,2)上單調(diào)遞增。

又注意到函數(shù)f(x)的圖像在x=2 處連續(xù)，所以可知：函數(shù)f(x)在(-∞,1)上單調(diào)遞減，在(1,+∞)上單調(diào)遞增，故所求函數(shù)f(x)的最小值為f(1)=2。

解法二（放縮法）：根據(jù)指數(shù)函數(shù)切線不等式ex≥ex（當(dāng)且僅當(dāng)x=1 時(shí)不等式取等號(hào)），可得ex-1≥x（當(dāng)且僅當(dāng)x=1時(shí)不等式取等號(hào)）。

又因?yàn)閨x-2 |≥2 -x（當(dāng)且僅當(dāng)x-2 ≤0 時(shí)不等式取等號(hào)），所以將這兩個(gè)同向不等式相加可得|x-2 |+ex-1≥2 -x+x=2，即f(x) ≥2，當(dāng)且僅當(dāng)即x=1 時(shí)不等式取等號(hào)，故所求函數(shù)f(x)的最小值為2。

變式5：函數(shù)f(x)=的最小值為________。

解析：本題是絕對(duì)值、指數(shù)函數(shù)、對(duì)數(shù)函數(shù)的綜合應(yīng)用，不便于運(yùn)用分類討論法進(jìn)行求解，從而需要考慮應(yīng)用放縮法。

根據(jù)指數(shù)函數(shù)切線不等式ex≥x+1（當(dāng)且僅當(dāng)x=0 時(shí)不等式取等號(hào)），可得3ex≥3x+3（當(dāng)且僅當(dāng)x=0時(shí)不等式取等號(hào)）①。

根據(jù)對(duì)數(shù)函數(shù)切線不等式得ln(1 +x) ≤(1 +x) -1，即ln(1 +x) ≤x（當(dāng)且僅當(dāng)x=0 時(shí)不等式取等號(hào)），所以-4 ln(1 +x) ≥-4x（當(dāng)且僅當(dāng)x=0 時(shí)不等式取等號(hào)）②。

三、備考策略

處理函數(shù)問題時(shí)，一方面要學(xué)會(huì)靈活運(yùn)用函數(shù)的性質(zhì)解題，具體包括構(gòu)造函數(shù)，利用導(dǎo)數(shù)分析函數(shù)的圖像與性質(zhì)，運(yùn)用函數(shù)的圖像與性質(zhì)分析、解決有關(guān)最值、值域問題以及參數(shù)的取值范圍問題等；另一方面要學(xué)會(huì)綜合運(yùn)用切線不等式、基本不等式、不等式的性質(zhì)等知識(shí)解題。

綜上，賞析考題的設(shè)計(jì)精妙之處，有助于教師拓寬命題思路，設(shè)計(jì)具有交匯性質(zhì)的創(chuàng)新試題；關(guān)注考題的優(yōu)解，有助于學(xué)生簡(jiǎn)捷求解，達(dá)到“秒殺”效果。當(dāng)然，讓學(xué)生體驗(yàn)解析過程的精妙之處，還能激發(fā)他們的解題靈感，培養(yǎng)他們的思維能力。