巧用導數知識 破解教學疑點
——由一個典型物理錯誤引發的思考
江蘇淮安市洪澤區教師發展中心(223100)程如林
一、問題的由來
在近年某省高考試卷中出現了這樣一道物理試題。
[例1]如圖1 所示,兩根平行金屬導軌固定在水平桌面上,每一根導軌每米長的電阻值為r0=0.10 Ω/m,導軌足夠長,導軌的端點P、Q用電阻可以忽略不計的導線相連,兩導軌間的距離l=0.2 m,空間有隨時間變化的勻強磁場垂直于桌面,已知磁感應強度B與時間t的關系為B=kt,比例系數為k=0.02 T·s-1。一電阻不計的金屬桿可以在導軌上無摩擦地滑動,在滑動過程中保持與導軌垂直。在t=0 時刻,金屬桿緊靠在P、Q端,在外力作用下,桿以恒定的加速度從靜止開始向導軌的另一端滑動,求在t=6.0 s時金屬桿所受到的安培力大小。
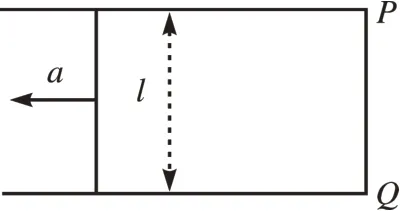
圖1
學生的解答普遍如下:

其實,這是錯誤的!
在當年的高考中,這道題的難度系數為0.077,錯誤率非常高。造成這一錯誤的原因是什么呢?
二、問題的剖析
經分析發現,這是由于教師在平時教學中對感應電動勢的計算公式沒有深入討論造成的。
在高中物理教材中,法拉第電磁感應定律的數學表達式為E=,教材在給出這一表達式后,僅討論了“導線切割磁感線時的感應電動勢”這一特殊情形,此情形下的感應電動勢表達式可簡化為E=Blvsinθ,如果導線垂直切割磁感線,則E=Blv,除此之外,教材中未討論其他情形下感應電動勢的表達式。
教師在平時教學中通常會討論以下兩種特殊情形:

在這樣的背景下,學生便記住了這兩種特殊情形下的公式,并學會了處理這兩種特殊情形下的電磁感應問題。
而本題的情形是磁感應強度B和面積S均發生了變化,這時如何計算感應電動勢呢?
由于教師平時沒有深入討論,學生也就不清楚如何計算,所以,當年遇到這種情形時,絕大多數學生在計算電動勢時就套用了公式E=Blv,結果當然是錯的。
這是一個沉痛的教訓,值得我們深刻記取。
那么,在平時的教學中,教師應該怎樣破解這一教學疑點呢?
三、問題的破解
其實,應用導數知識,問題便迎刃而解了,具體分析如下:
因為,瞬時電動勢E而Φ=BS(其中B,S均為變量)。
由導數公式可得:
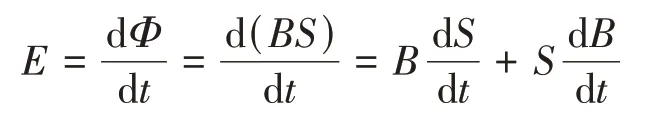
這就是B,S均發生變化時感應電動勢的一般計算公式,這是一個推廣公式。
不難發現,等式右邊有兩項,教師應對這兩項的物理意義做進一步的解釋。
第一項是由于運動(即S變化)而產生的電動勢,叫作動生電動勢,第二項是由于磁場變化(即B變化)而產生的電動勢,叫作感生電動勢,總的感應電動勢是這兩個電動勢的代數和。
至此,可得到上述試題的正確解法如下:
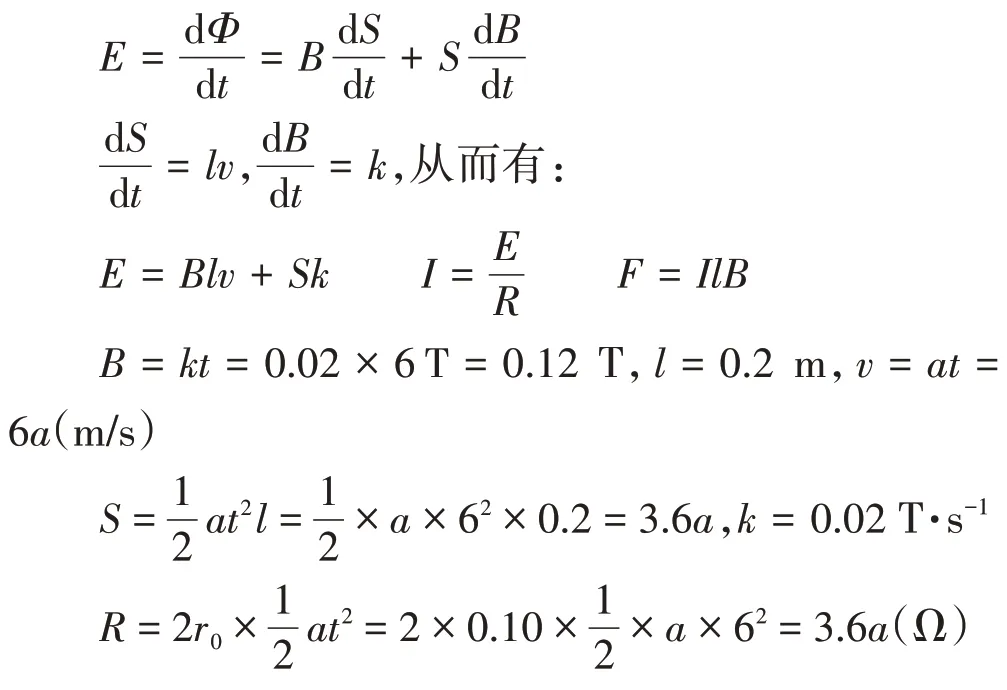
綜合以上各式求解得F=1.44 × 10-3N
這才是正確的解答。至此,學生終于對這個問題有了清晰的認識。
四、問題的拓展
為了強化相關內容的教學,教師還可對這道題進行拓展,具體如下。
[例2]如圖2 所示,直角形金屬導軌APQ固定在水平桌面上,導軌每米長的電阻值為r0=0.10 Ω/m,導軌足夠長,空間有隨時間變化的勻強磁場垂直于桌面,已知磁感應強度B與時間t的關系為B=kt,比例系數為k=0.02 T·s-1。兩個電阻不計的金屬桿CD、EF可以在導軌上無摩擦地滑動,在滑動過程中,金屬桿CD保持與導軌PQ垂直,金屬桿EF保持與導軌AP垂直,金屬桿足夠長。在t=0 時刻,金屬桿CD緊靠金屬導軌AP,金屬桿EF緊靠金屬導軌PQ,在外力作用下,金屬桿EF以恒定加速度a1=0.3 m·s-2從靜止開始向左滑動,金屬桿CD以恒定加速度a2=0.2 m·s-2從靜止開始向下滑動,已知金屬桿與金屬桿之間、金屬桿與導軌之間接觸良好,求在t=1.0 s時金屬桿EF所受到的安培力的大小。
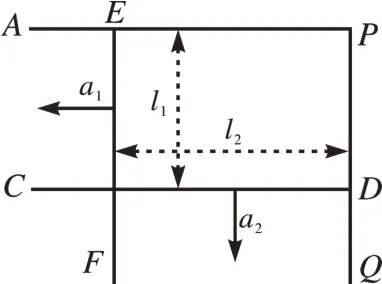
圖2
分析:在本例中,有三個因素對感應電動勢有影響,分別是磁感應強度隨時間變化、金屬桿EF水平向左運動、金屬桿CD豎直向下運動,即存在三個變量,這時怎么計算感應電動勢呢?
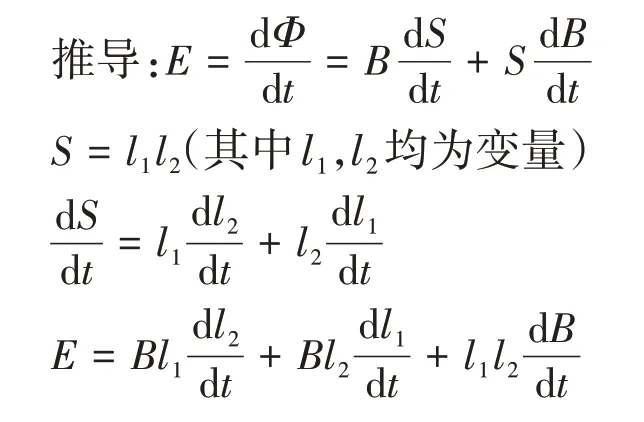
此式即存在三個變量時的感應電動勢的計算公式。

綜合以上各式求得:F=1.2 × 10-4N
五、問題的質疑
質疑1:在例1 中,總電動勢的計算公式是E=Blv+Sk;在例2 中,總電動勢的計算公式是E=Bl1v1+Bl2v2+Sk,在這兩種情形下,等號右邊各項都是大小相加的,這樣計算有沒有問題呢?
下面進行探討:
對例1,不妨假設磁場方向是垂直紙面向外的,則由右手定則可知,由于金屬桿運動而產生的動生電流的方向是沿桿向上的,在回路中是順時針方向的;再由楞次定律可知,由于磁場變化而產生的感生電流的方向也是順時針方向的。可見,兩者方向是一致的,如果取順時針方向為正方向,則等號右邊各項均取正值,而且是大小相加的。
對例2,同理分析可知,等號右邊各項也應是大小相加的。
結論1:對例1 和例2,關于總電動勢的計算公式,等號右邊各項是大小相加的,這樣計算沒有問題。
質疑2:是否在任何情況下,等號右邊各項都是大小相加的呢?下面通過例3進行探討。
[例3]如圖3 所示,直角形金屬導軌APQ固定在水平桌面上,導軌每米長的電阻值為r0=0.10 Ω/m,導軌足夠長,空間有隨時間變化的勻強磁場垂直于桌面,已知磁感應強度B與時間t的關系為B=kt,比例系數為k=0.02 T·s-1。兩個電阻不計的金屬桿CD,EF可以在導軌上無摩擦地滑動,在滑動過程中,金屬桿CD保持與導軌PQ垂直,金屬桿EF保持與導軌AP垂直,已知金屬桿EF向右勻速運動,速度大小為v1=0.3 m/s,金屬桿CD向上勻速運動,速度大小為v2=0.2 m/s,在t=1.0 s時,l1=0.1 m,l2=0.15 m,已知金屬桿與金屬桿之間、金屬桿與導軌之間接觸良好,求t=1.0 s 時金屬桿EF所受到的安培力大小。
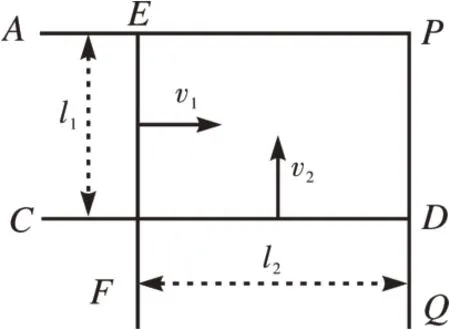
圖3
分析:在本例中,存在三個變量,即有如下三個因素影響感應電動勢。
金屬桿EF水平向右運動,由此產生的動生電動勢:E1=
金屬桿CD豎直向上運動,由此產生的動生電動勢:E2=
磁感應強度隨時間變化,由此產生的感生電動勢:E3=
這時總感應電動勢應該怎樣計算呢?
不妨假設磁場方向是垂直紙面向外的,分別考慮上述三個因素產生的感應電流方向。
因金屬桿EF水平向右運動,由右手定則可知,產生的動生電流方向沿桿向下,對回路來說,是逆時針方向。
因金屬桿CD豎直向上運動,由右手定則可知,產生的動生電流方向沿桿向右,對回路來說,是逆時針方向。
因磁感應強度隨時間變化,由楞次定律可知,產生的感生電流方向是順時針方向。
因此,若取逆時針方向為正方向,則總電動勢為:E=Bl1v1+Bl2v2-Sk
這就是例3中總感應電動勢的計算公式。
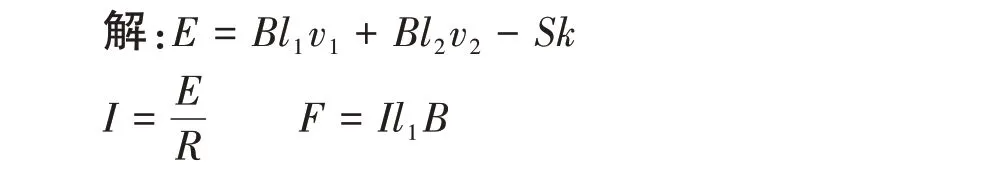
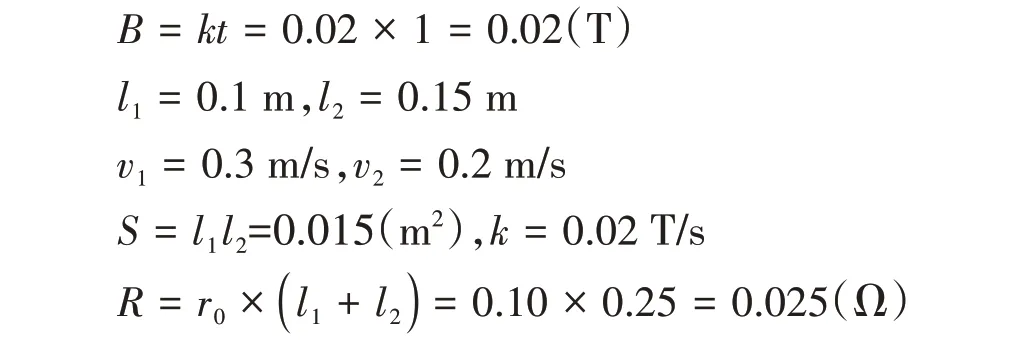
綜合以上各式求得F=7.2 × 10-5N
結論2:通過例3的分析可知,對由多個因素引起的電磁感應現象,關于總感應電動勢的計算公式,等號右邊各項是相加還是相減或是混合加減,這個問題要分別運用右手定則和楞次定律對各個因素引起的感應電流方向進行判斷,再綜合判斷等號右邊各項是相加還是相減或是混合加減。在本文列舉的例1和例2中,經判斷是各項大小相加;在例3中,經判斷是各項大小混合加減。
六、問題的反思
教師在平時教學中,對新的物理規律,不能只是簡單交代一下物理公式就開始進行習題訓練,而應加強對物理公式的深入討論,弄清公式的來龍去脈,搞清公式的推導過程,對一些有疑惑而又必須進行拓展和推廣的公式,要展開討論,要通過各種方法讓學生深刻理解物理公式,讓學生在理解的基礎上記住公式。只有這樣,學生才能準確運用公式。
導數是非常重要的數學知識,在大學物理中導數有著非常廣泛的應用。在新課程背景下,導數已被編入高中數學教材,而且屬于主干知識,教材中專門編有一章內容“導數及應用”,介紹導數的基本概念、計算公式及實際應用,其中包括許多用導數知識處理物理問題的案例。有了高中數學中的導數知識做基礎,在高中物理教學中,教師便可以用導數知識處理物理問題,這符合新課程的教學理念。

