大型復雜系統多態可靠性快速評估算法

史躍東，金家善，柴 凱

（海軍工程大學艦船與海洋學院，湖北 武漢 430033）

0 引 言

可靠性作為一類反映裝備通用質量特性的固有屬性，直接影響裝備的固有性能與使用效能發揮，進而決定裝備執行任務的成功與否。研究裝備的可靠性，對于改善裝備質量特性，優化裝備保障管理，增強裝備使用效能，提升裝備執行任務能力，具有重要工程應用價值與現實經濟意義。近年來，隨著現代科技與制造業水平的迅猛發展，裝備的結構組成日趨復雜，多呈現大型化、集成化、精細化、耦合化等特點。同時，與其相關的可靠性分析、設計、評估等工作，也日趨復雜與困難。為此，衍生出諸多新的可靠性研究方向。裝備復雜系統多狀態可靠性研究，即為其中比較具有代表性的重點和熱點研究方向，且發展迅速、成果豐碩［1-3］。

有關裝備復雜系統多狀態可靠性的研究工作，大體可分為4類。第1類基于經典馬爾可夫狀態躍遷模型，通過多粒度割分傳統的裝備二元功能狀態，建立不同狀態間的躍遷微分方程，實現裝備復雜系統的多狀態可靠性建模、分析與評估，但存在指數分布模型假設的工程約束困境［4-7］，以及大維度狀態躍遷微分方程解算的技術瓶頸［8-11］，此外相關系統狀態的工程分辨解析程度也大大受到限制［12-15］。第2類基于半馬爾可夫狀態躍遷模型，通過構建非指數分布約束的嵌入式馬爾可夫鏈，并引入核矩陣函數，有效改善了裝備復雜系統的多狀態可靠性建模、分析與評估精度［16-18］，但仍面臨大維度狀態解算的技術瓶頸［19-21］。第3類基于通用生成函數技術，通過定義不同結構單元的通用生成函數，并結合系統不同層級間的構型耦合關聯，完成裝備復雜系統的通用生成函數求解與多狀態可靠性解析，有效規避了直接解算大維度狀態模型的技術困境［22-25］，但本質上仍只是進行了降維變換，對超大系統或巨系統應用效果欠佳［26-29］。第4類基于蒙特卡羅仿真技術，通過生成貼近狀態駐留時間隨機分布的偽隨機量值，模擬裝備復雜系統的邏輯事件歷程，進而利用數理統計方法，獲取多狀態裝備復雜系統的可靠性能，但對于先驗分布的判斷以及仿真數據的體量要求較高［30-32］。

綜上，4類研究工作雖能較好地解決部分裝備復雜系統的可靠性建模、分析與評估問題，并已在當今機械、電力、能源、軍事、信息網絡等領域發揮了重要作用，但對于組件構成龐大的大型（或巨型）裝備復雜系統來說，利用前述4類工作的階段研究成果，開展其多狀態可靠性的分析與評估工作，無論是在計算資源的依賴性上，還是在解算方法的可實現性與便捷性上，都還或多或少地存有技術短板，亟待深入探索、逐步完善。

本文以工程上組件構成眾多的大型裝備復雜系統為研究對象，旨在通過合理構建面向不同系統狀態耦合結構的極限序列核，探索一類計算資源要求低、計算便捷，且逼近精度滿足工程需要的多狀態可靠性建模、分析與快速評估方法，力求豐富與突破大型裝備復雜系統多狀態可靠性研究的關注方向和技術途徑。

1 大型多狀態裝備系統

1.1 大型多狀態系統

任意大型多狀態裝備系統A，由k個子系統B i組成，i＝1，2，…，k，k∈N；每個子系統Bi包含l i個組成元件U ij，j＝1，2，…，l i，l i∈N；系統A使用過程中，元件U ij的輸出性能可能逐步退化，存在s＋1種輸出狀態，s∈N；同時，可能有多樣作用于系統A的外在載荷，存有p＋1種運行工況要求，p∈N；并且有如下前提假設和符號約定：

（1）不同元件U ij的性能退化隨機歷程可測，且關鍵退化狀態節點的認定規則相似；

（2）系統A與任意元件U ij的輸出狀態索引集合為｛0，1，…，s｝，其中索引0代表最劣狀態，索引s代表最優狀態，自索引0至索引s，狀態水平依次升高；

（3）系統A的運行工況索引集合為｛0，1，…，p｝，各工況運行可能出現的概率為qz，z∈｛0，1，…，p｝，qz∈［0，1］；

（4）u ij（t，z）、a（t，z）：第z種 工況下，u ij（t，z）和a（t，z）分別為元件U ij、系統A自最優狀態s觸發后t時刻所處的狀態水平，其中，t∈［0，∞）；

（5）T ij（v，z）：第z種工況下，元件U ij自最優狀態s觸發，保持u ij（t，z）∈狀態子集｛v，v＋1，…，s｝的獨立隨機變量，T ij（v，z）反映元件U ij處于不同狀態子集的駐留時間。其中，v∈｛0，1，…，s｝；

（6）T（v，z）：第z種工況下，系統A自最優狀態s觸發，保持a（t，z）∈狀態子集｛v，v＋1，…，s｝的隨機變量，T（v，z）反映系統A處于不同狀態子集的駐留時間。其中，v∈｛0，1，…，s｝。

1.2 多狀態系統可靠性

遵循前述假設與符號約定，統一選用可靠度函數R（t）作為度量大型多狀態裝備系統A可靠性的量化參數，則有：

（1）元件U ij可靠度

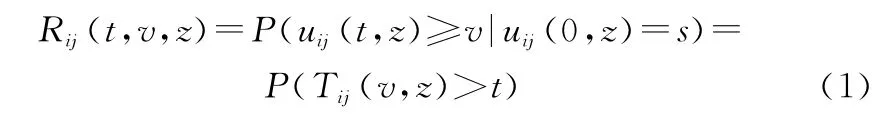
式中：P（·）為絕對概率函數；P（·|·）為條件概率函數；Rij（t，v，z）為z工況下元件U ij處于狀態子集｛v，v＋1，…，s｝的可靠度函數。

（2）系統A可靠度

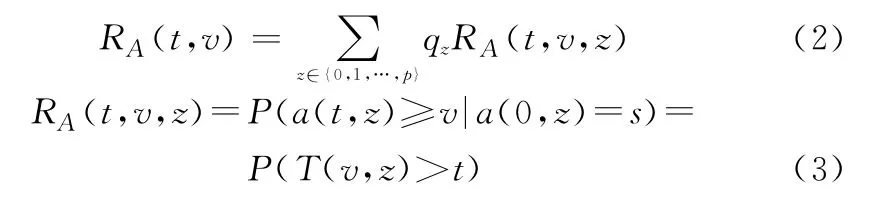
式中：RA（t，v）為系統A處于狀態子集｛v，v＋1，…，s｝的可靠度函數；RA（t，v，z）為z工況下系統A處于狀態子集｛v，v＋1，…，s｝的可靠度函數。

（3）系統A狀態分布

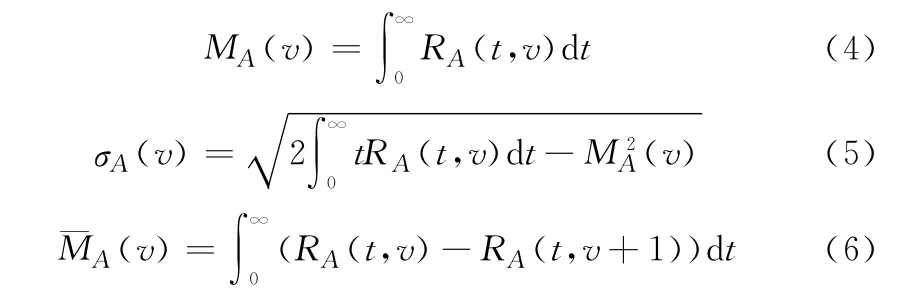
式中：MA（v）為系統A駐留于狀態子集｛v，v＋1，…，s｝的平均期望時間；σA（v）為平均期望時間MA（v）的標準方差；（v）為系統A駐留于狀態v的平均期望時間。

1.3 元件與系統的耦合關聯

元件U ij與系統A間的耦合結構不同，相關狀態耦合關系也不同。此處，僅就多狀態裝備復雜系統可靠性研究中，較具代表性的兩類耦合結構，說明如下。

（1）串并耦合結構：

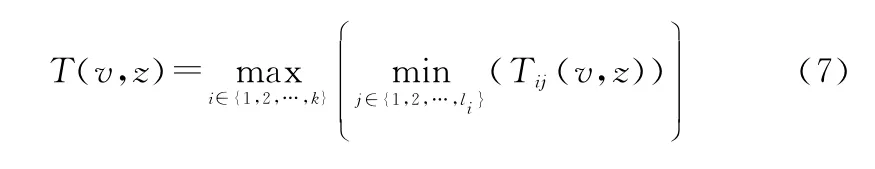
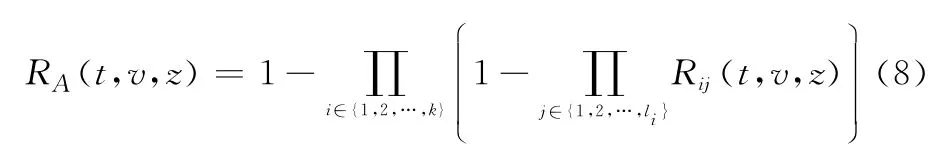
式（7）和式（8）反映了大型串并耦合裝備系統z工況下元件與系統之間狀態駐留時間和可靠度的耦合關聯。現實工程中的大型分布式能源供應系統（如天然氣、原油等），多為此類狀態耦合結構。

（2）并串耦合結構：

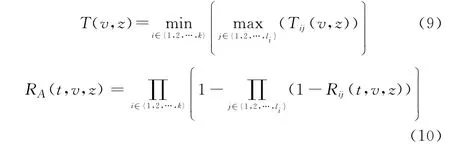
式（9）和式（10）反映了大型并串耦合裝備系統z工況下元件與系統之間狀態駐留時間和可靠度的耦合關聯。現實工程中的大型纜索牽引系統、光纖網絡信息傳導系統等，多為此類狀態耦合結構。

觀察前述各式可知，如果直接利用式（8）和式（10），解算評估大型裝備復雜系統的多狀態可靠性，在已知元件U ij的可靠度函數Rij（t，v，z）前提下，至少還需實施l1×l2×…×l k次乘法運算。對于大型裝備復雜系統來說，k與l i的取值通常較大（k＞10，l i＞10），此時若想實現系統可靠度的精確解算，所需占據的計算機資源往往較多，解算耗費時間也往往較長。本文嘗試采用恰當的數學預處理方式，在保證工程逼近精度的前提下，大幅度提升大型裝備復雜系統的多狀態可靠度求解效率。為此，引入極限序列核的概念。

2 極限序列核

由式（3）易知，系統A的可靠度本質上體現為隨機變量T（v，z）的概率分布特征。因此，如果能夠通過恰當的數學變換處理，將隨機變量T（v，z）的概率分布，映射于某一已知的標準概率分布空間，則可直接利用已知標準概率分布空間的諸多數學特征，反向解算系統A的可靠度。進一步，如果對于任意大型裝備復雜系統A，存在序列對〈Φ（n，v，z），Ψ（n，v，z）〉，n∈N，使得式（11）和式（12）同時成立，則稱這類與系統A組成結構和元件U ij數目密切相關的序列對為用于解算系統A可靠度的極限序列核。

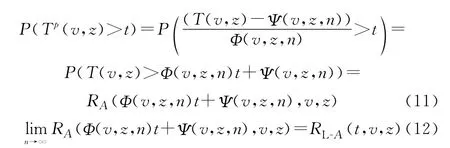
式中：T p（v，z）為經過數學變換預處理后系統A的狀態駐留時間隨機變量；RL-A（t，v，z）為系統A的極限可靠度函數；n為與k、l i相關的反映系統A總體元件組成的序列數。

繼而，如果在函數RL-A（t，v，z）的連續時間點集CR-L-A上，可以找到這樣的極限序列核，則當系統A的組成元件個數n足夠大時，可近似逼近系統A的可靠度函數R A（t，v，z）如下：

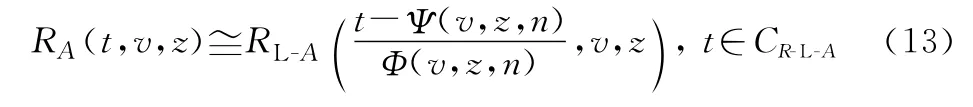
需要說明的是，工程上大型裝備復雜系統的結構組成與耦合模式多樣，并不一定能夠找到符合式（11）和式（12）變換要求的極限序列核。但對于符合齊次和規則特征的大型裝備復雜系統而言，通常可以通過恰當的數學手段，找出符合要求的極限序列核，且并不唯一。

3 大型裝備系統可靠性快速算法

以符合齊次和規則特征的大型并串耦合結構系統為例，示例說明大型裝備復雜系統的極限序列核的確定過程，以及相關多狀態可靠性的快速分析與評估算法。如圖1所示，某大型裝備復雜系統的元件組成與并串耦合結構，符合齊次和規則特征，即對任意i，j取值，均有

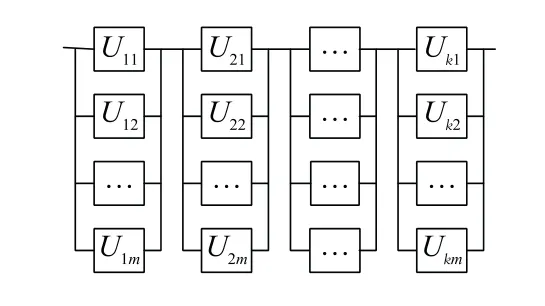
圖1 齊次并串耦合規則系統可靠性框圖Fig.1 Reliability scheme of a homogeneous parallel-series coupling regular system

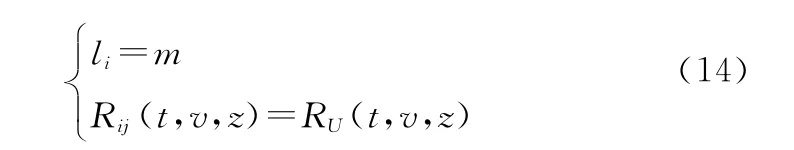
式中：m為齊次規則系統各子系統所包含的元件數；RU（t，v，z）為齊次規則系統各組成元件的多狀態可靠度函數。

為便于后續算法結論的演繹說明，給出如下引理。

3.1 算法引理

對于滿足齊次和規則約束條件的任意大型并串耦合系統A，取k＝n，且存在正整數c1，c2，使得m-c1lnn?c2成立。

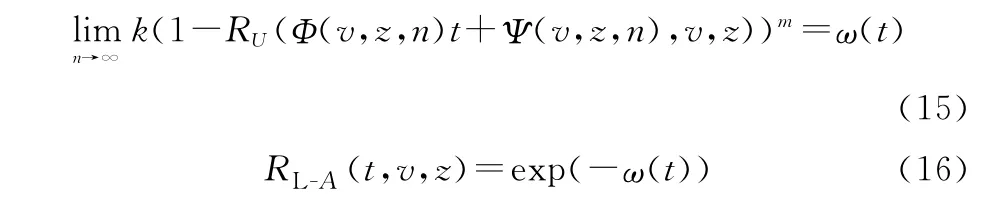
如果其極限序列核〈Φ（n，v，z），Ψ（n，v，z）〉和極限可靠度函數RL-A（t，v，z）存在，當且僅當式（15）給出的序列函數極限存在，且此時系統A的極限可靠度函數RL-A（t，v，z）應具有式（16）所示指數函數表達形式。

上述引理的證明較為繁瑣復雜［33-34］，此處直接引用結論。

3.2 算法示例

進一步，假設大型并串耦合系統A組成元件的多狀態可靠度滿足威布爾分布特征［35］，即

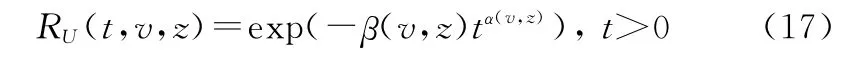
式中：α（v，z）、β（v，z）為與系統工況和元件狀態相關的威布爾分布常量。由前述引理，可嘗試構建系統A的極限序列核如下：

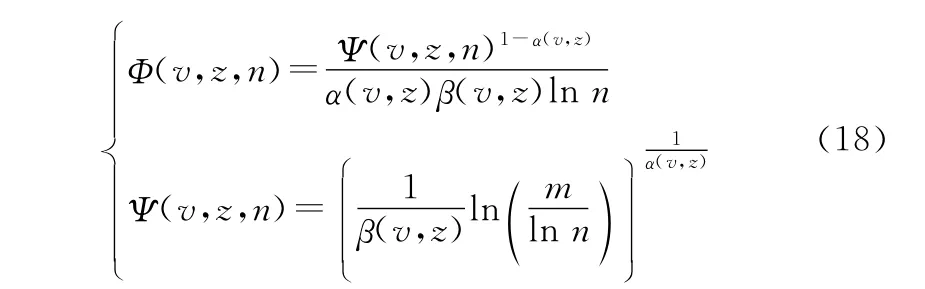
式中：ln（·）為指數底的對數函數。則有

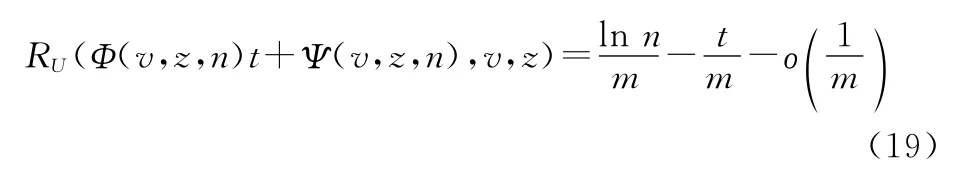
式中：o（·）為高階無窮小函數。再依據式（15），有

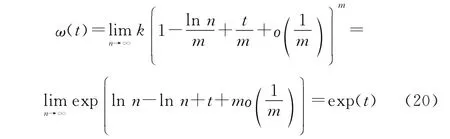
進而，依據式（16），有

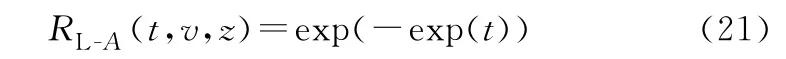
至此，可實現大型并串耦合系統A的多狀態可靠性快速分析與評估如下：

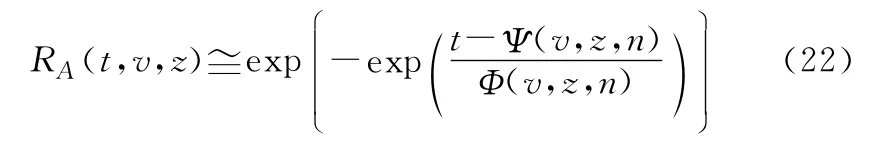
對比式（10）和式（22）的數學表達形式可知，引入極限序列核的快速算法，避開了傳統并串耦合系統可靠性解析分析中的大量級疊乘運算，直接利用系統的極限可靠度函數RL-A（t，v，z）逼近原并串耦合系統的多狀態可靠性特征，雖在求解問題的技術難度上有所增加，但大大提升了解算問題的工作效率。

4 應用案例

4.1 船用升降轉運系統

某船用升降轉運系統由傳動馬達、牽引鋼索、載重平臺、電控裝置4個分系統組成，相關系統可靠性框圖如圖2所示。鑒于牽引鋼索長期暴露于高溫、高濕、高鹽度、雨水、曝曬、腐蝕等海洋惡劣工作環境，且頻繁承受升降載荷的直接沖擊，因此船用升降轉運系統的可靠性能主要取決于牽引鋼索分系統的可靠性能，即。

圖2 升降轉運系統可靠性框圖Fig.2 Reliability scheme of a lifting and transferring system

其中，牽引鋼索分系統由12根特種鋼索組成，每根鋼索的承力狀態下降，均會直接導致整個牽引鋼索分系統的工作狀態下降。每根特種鋼索又分別由12根外側鋼縷絲和14根內側鋼縷絲扭繞組成，相關橫截面結構如圖3所示。升降轉運系統工作時，鋼索內部的26根鋼縷絲同時承受轉運載荷的沖擊，并呈現并聯受力狀態。內外側鋼縷絲雖幾何尺寸不同，但可靠性能相同，均滿足威布爾分布特征［36］。

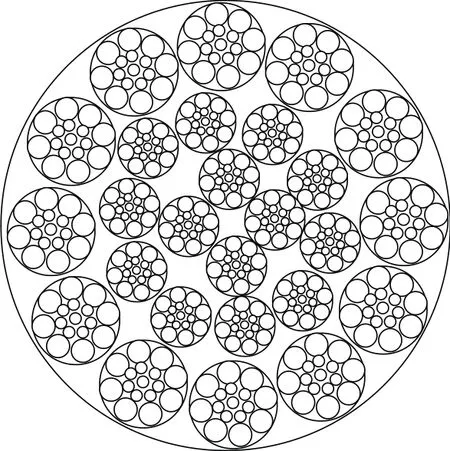
圖3 特種鋼索橫截面結構Fig.3 Cross-section structure of the special steel cable

4.2 系統多狀態多工況說明

基于前文關于船用升降轉運系統各分系統及組成構件工作特征的闡述，可將其簡化為一類齊次規則并串耦合系統（k＝12，m＝26）。系統（組件）使用過程中，可能遭遇以下不同輸出狀態與運行工況。

（1）多狀態說明

升降轉運系統的牽引鋼索在海上惡劣環境中長期使用，將會逐漸產生性能退化，呈現4類狀態輸出水平，如表1所示。

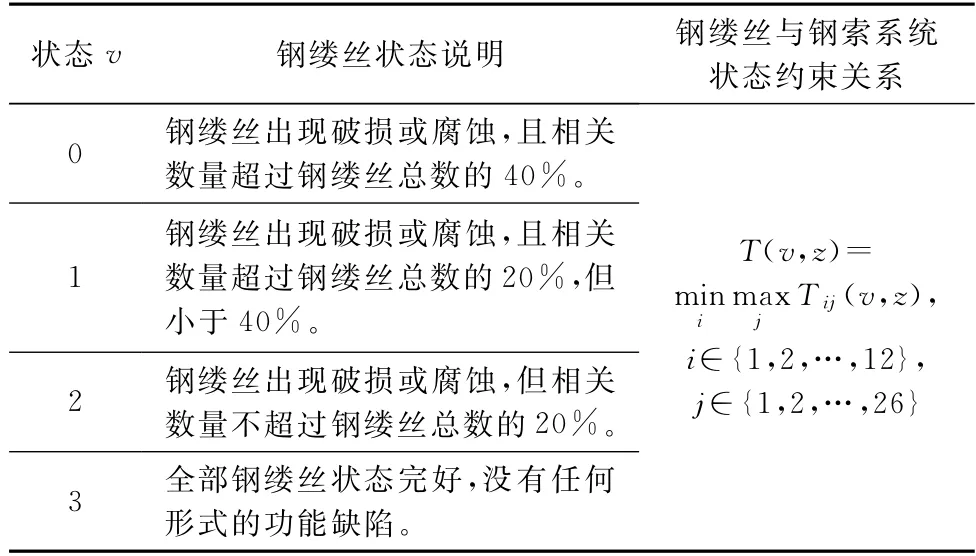
表1 牽引鋼索4類狀態輸出Table 1 Four output states of traction cable

表1中，T ij（v，z）為z工況下鋼縷絲自狀態3觸發，處于｛v，v＋1，…，3｝狀態子集的隨機駐留時間變量；T（v，z）為牽引鋼索分系統處于｛v，v＋1，…，3｝狀態子集的隨機駐留時間變量。

（2）多工況說明

升降轉運系統的牽引對象多樣，不同載荷作用下，牽引鋼索的可靠性能并不盡一致。依據升降轉運系統歷次執行任務的年度數據，經承力載荷聚類統計分析，可將其工況分為4類，如圖4所示。

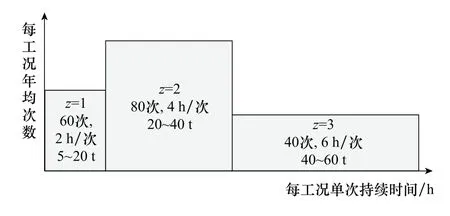
圖4 4類工況的年平均分布情況Fig.4 Annual average distribution of four working conditions

圖4中，載荷度量單位為t，時間度量單位為h；工況3代表轉運載荷處于40～60 t，年均40次，每次任務持續6 h；工況2代表轉運載荷處于20～40 t，年均80次，每次任務持續4 h；工況1指轉運載荷處于5～20 t，年均60次，每次任務持續2 h。轉運載荷小于5 t，或無轉運任務，統一視為工況0。由此，可知4類工況在升降轉運系統年度使用過程中的發生概率qz，z∈｛0，1，2，3｝，如表2所示。

表2 4類工況的年度發生概率Table 2 Annual probability occurrence of four working conditions

4.3 系統極限序列核解算

參考文獻［37］中有關繩索的可靠性數據，以及業內專家的部分實踐經驗，取單位時間尺度為年，則有鋼縷絲的多狀態可靠性威布爾分布常量α（v，z）、β（v，z），如表3所示。

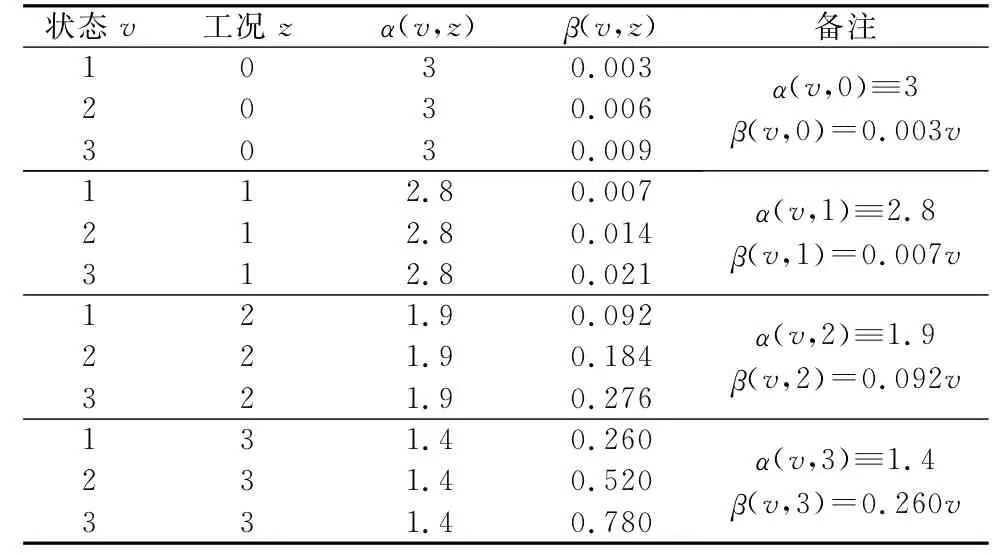
表3 威布爾分布常量α（v，z）、β（v，z）Table 3 Weibull distribution constantsα（v，z）andβ（v，z）

進而，由式（18）可知，升降轉運系統4類工況下的多狀態極限序列核〈Φ（12，v，z），Ψ（12，v，z）〉如表4所示。

表4 極限序列核〈Φ（12，v，z），Ψ（12，v，z）〉Table 4 Limit sequence kernel〈Φ（12，v，z），Ψ（12，v，z）〉

4.4 系統可靠性評估

進一步，基于式（2）和式（22），以及表2和表4的計算結果，可知升降轉運系統的多狀態可靠度函數R（t，v）快速逼近表達式：

鑒于篇幅所限，此處僅給出R（t，1）的快速逼近表達式。

進而，基于式（4）～式（6），可知升降轉運系統駐留于狀態子集｛v，v＋1，…，s｝中的平均期望時間M（v）和平均期望方差σ（v），以及駐留于狀態v的平均期望時間ˉM（v）。相關數值解算結果如圖5、圖6和表5所示。其中，時間t的度量單位y表示年，p（t，v）為系統駐留于狀態v的概率。

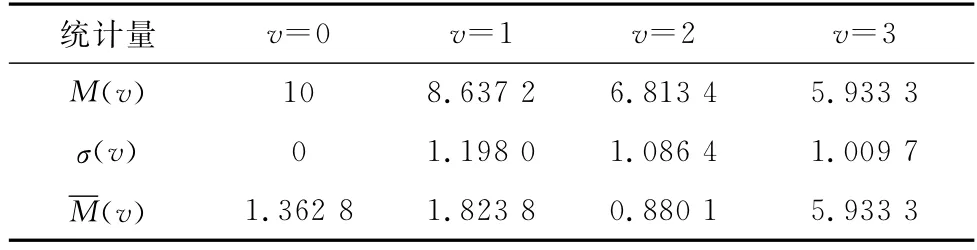
表5 系統狀態駐留時間T（v，z）統計特征Table 5 Statistical characteristic of system state dwell time T（v，z）

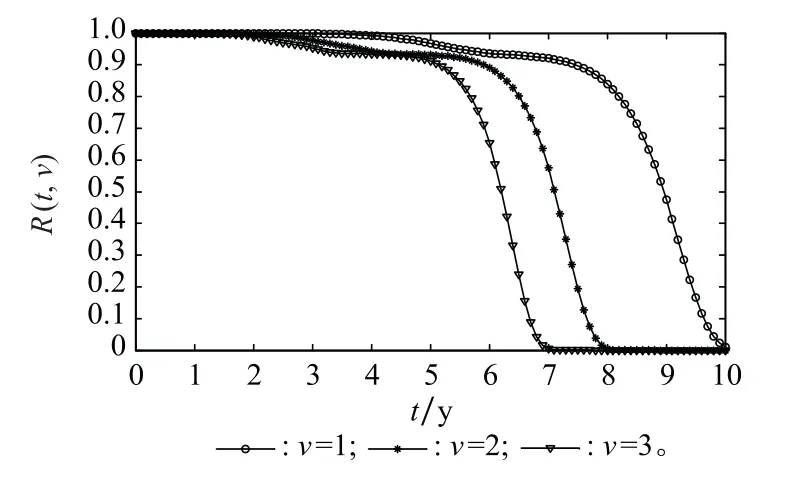
圖5 升降轉運系統多狀態可靠度函數R（t，v）Fig.5 Multi-state reliability function R（t，v）of the lifting and transferring system

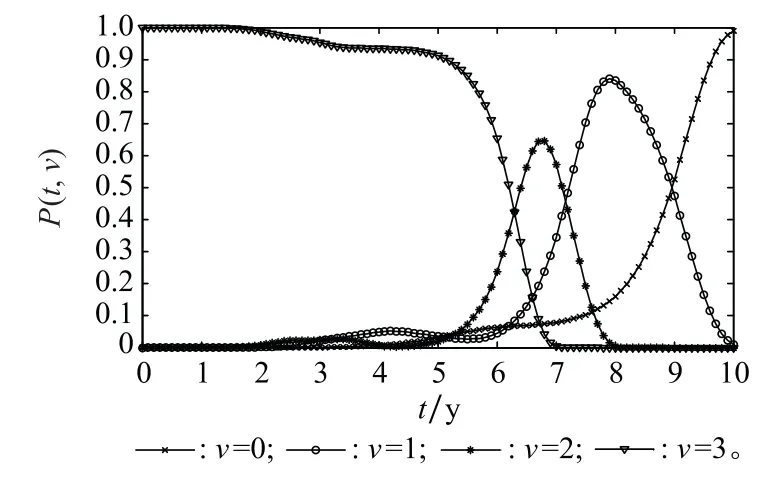
圖6 升降轉運系統處于不同狀態的概率p（t，v）Fig.6 Probability function of the lifting and transferring system in different states

觀察圖5中的可靠度曲線和圖6中的狀態概率曲線可知：系統自最優狀態觸發，隨著使用時間的增長，處于狀態子集｛v，v＋1，…，3｜v≠0｝的可靠度呈現單調下降趨勢（不考慮維修）；歷經約5 y左右時間，系統處于上述各狀態子集的可靠度，均會出現迅速衰減，其中可靠度R（t，3）的衰減速度最大；同時，自5 y左右時間起，系統位于最優狀態的概率p（t，3）迅速下降，而位于其他劣化狀態的概率迅速上升；3～5 y時間階段，系統牽引功能狀態水平逐步趨于劣化，持續運行的安全風險較大，工程技術人員應對這一時間階段給予充分關注，必要時提前安排相關預防性維修活動。

觀察表5中的狀態駐留時間T（v，z）統計特征數據可知：10 y使用周期內，系統處于最優狀態的期望時間最長，約為5.93 y；若取v＝2為系統風險評估的關鍵辨識狀態，則系統處于可接受狀態子集｛2，3｝的期望時間，約為6.81 y；處于不可接受狀態子集｛0，1｝的期望時間，約為3.19 y。進一步，取系統最高可接受的風險門限為r＝0.05。

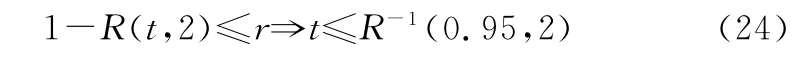
式中：R-1（·）為系統可靠度函數的逆函數；0.95為與風險門限對應的系統最低可接受的可靠度量值。由式（24）可知，為確保系統日常使用中的風險可控、可接受，其持續使用時間t，不應超過3.8 y。

4.5 快速算法效能評估

從解算速度和數值誤差兩個方面，評估前述極限序列核快速逼近算法的解算效能。

（1）解算速度評估

對于案例所述齊次規則情形，式（10）所示大型并串耦合系統的解析表達式退化為

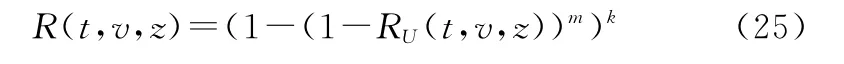
式中：R（t，v，z）、RU（t，v，z）分別為z工況下升降轉運系統和鋼縷絲處于狀態子集｛v，v＋1，…，3｝的可靠度函數。由此，基于式（2），可得系統的多狀態可靠度函數R（t，v）的解析表達式如下：

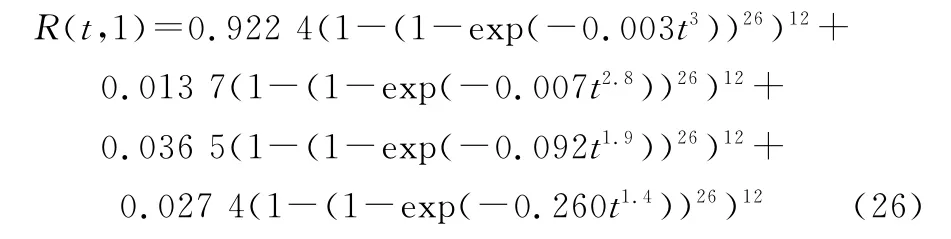
同樣，鑒于篇幅所限，此處僅給出R（t，1）的解析表達式。對比式（23）和式（26）可知：式（23）僅需執行兩次嵌套形式的指數函數運算，即可完成z工況下系統可靠度函數R（t，v，z）的快速逼近求解；而式（26）則需至少執行312次內含指數函數的多項式乘法運算才能完成。

針對文中案例，采用相同硬件平臺Thinkcenter M910t、軟件語言Matlab R2014和邏輯編程結構for循環語句，分別基于極限序列核快速逼近算法和直接解析算法，實現轉運系統多狀態可靠度函數R（t，v）的自動化數值求解。解算步長取0.1，解算時長取10，則完成轉運系統全部404個多狀態可靠度量值運算的耗時對比情況如表6所示。

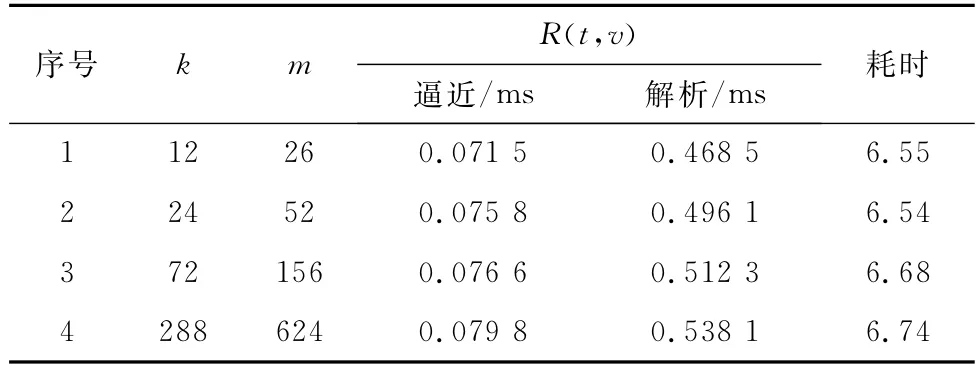
表6 兩類算法運算耗時比較Table 6 Comparison of computing time between two algorithms

觀察表6中的數據可知：極限序列核快速逼近算法的數值解算速度，約為直接解析算法的6.5～6.7倍，解算速度優勢明顯；雖然兩類算法的解算耗時，均保持在10-2～10-1ms級，但對于可能涵蓋大量級類似案例系統的巨型裝備復雜系統而言，極限序列核快速逼近算法的應用潛能更為突出。

（2）數值誤差評估

圖7為分別基于極限序列核快速逼近算法和直接解析算法，數值解算轉運系統多狀態可靠度函數R（t，v）的曲線對比圖。圖8為兩類算法間的解算數值差函數e（t，v）曲線分析圖。

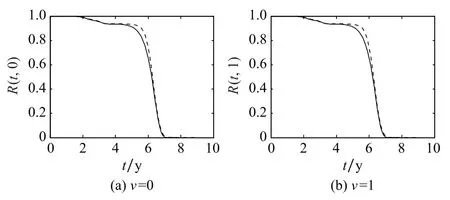
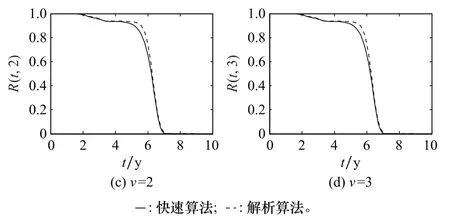
圖7 快速算法與解析算法的可靠度解算量值對比Fig.7 Comparison of reliability measures between fast algorithm and analytic algorithm

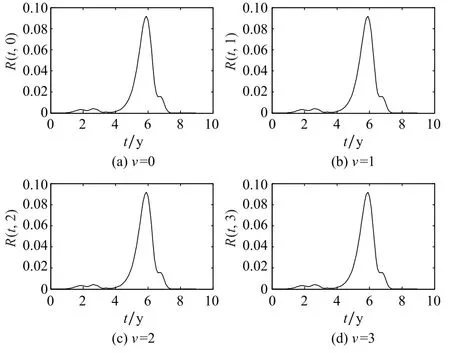
圖8 快速算法與解析算法的可靠度解算量值差Fig.8 Difference of reliability measures between fast algorithm and analytic algorithm

觀察圖7和圖8中的曲線可知：極限序列核快速逼近算法與直接解析算法的數值解算結果基本一致，尤其是在0～4 y時間段內，兩者數值高度吻合；從10 y總體使用周期來看，極限序列核快速逼近算法給出的系統可靠度量值偏于保守，均小于同時間點的直接解析算法量值；此外，與其他時間段相比，4～7 y時間段內，兩者解算的可靠度量值差距較大，峰值可達0.091 8、占比約10%，建議工程應用中，根據實際需求視情修正。

圖9為極限序列核快速逼近算法與直接解析算法在風險預報點的可靠度量值差圖。由圖9可知，臨界風險時刻兩類算法給出的可靠度量值差僅為0.001 6，與風險預報時間基本吻合。

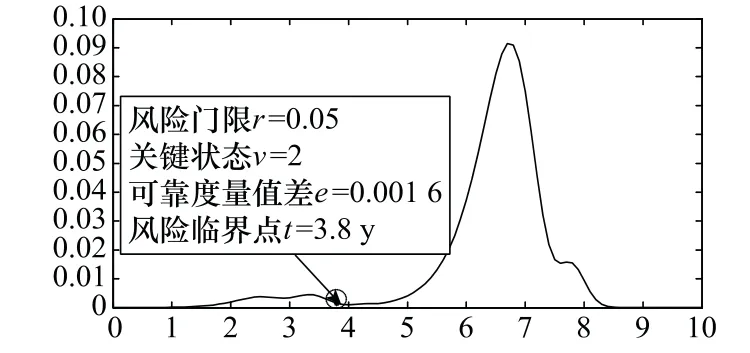
圖9 快速算法與解析算法風險預報點的可靠度量值差Fig.9 Difference of reliability measures between fast algorithm and analytic algorithm at risk forecast point

（3）量值差彌補方法

由前述分析可知，基于式（18）明確的極限序列核，解算系統的多狀態可靠度函數R（t，v）量值偏于保守。這里，構建另外一類解算結果偏于樂觀的極限序列核〈Φg（n，v，z），Ψg（n，v，z）〉如下所示：

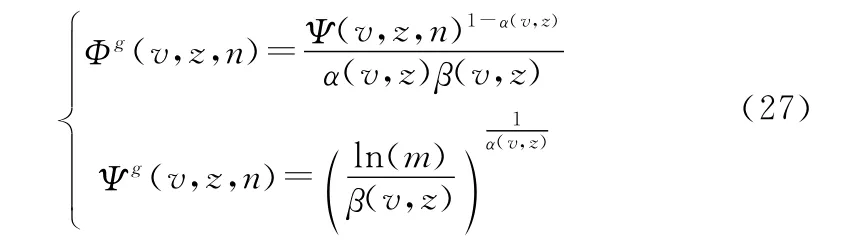
同樣，可由下式實現系統多狀態可靠度函數R（t，v）的快速逼近：

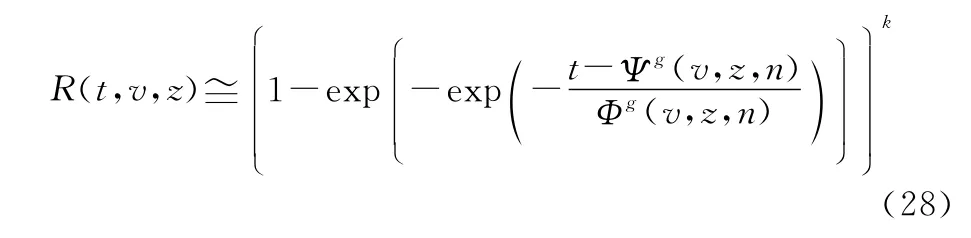
圖10為基于兩類不同極限序列核，系統多狀態可靠度解算量值對比情況。其中，極限序列核〈Φ（n，v，z），Ψ（n，v，z）〉對應快速逼近算法1（基于式（18）確定極限序列核），極限序列核〈Φg（n，v，z），Ψg（n，v，z）〉對應快速逼近算法2（基于式（27）確定極限序列核）。

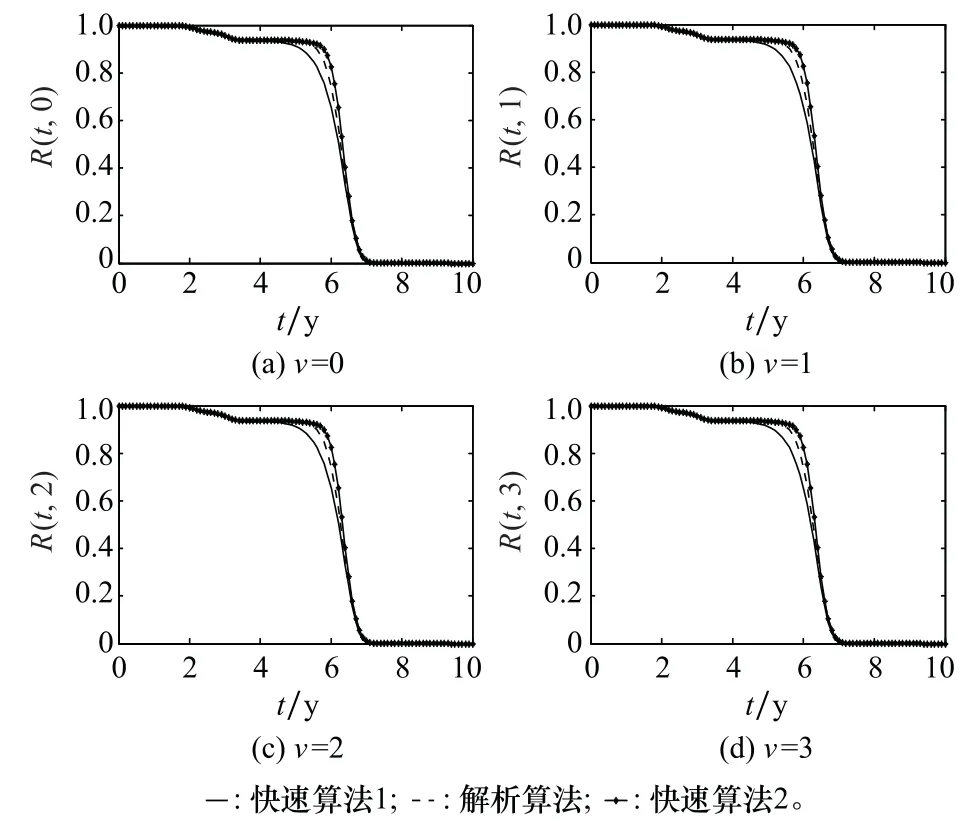
圖10 不同極限序列核下系統可靠度解算量值對比Fig.10 Comparison of reliability measures under different limit sequence kernels

由圖10可知，兩類極限序列核快速逼近算法給出的系統多狀態可靠度量值曲線，分別處于解析算法量值曲線的下方與上方。為此，綜合兩類極限序列核逼近算法，即可有效預測系統多狀態可靠度函數R（t，v）的解析值潛在區間，從而合理規避過于耗費計算資源的直接解析運算，并確保所獲可靠度解算量值的誤差充分可控。

5 結束語

針對工程大型裝備復雜系統，通過合理構建面向不同系統耦合結構的極限序列核和極限可靠度函數，探索了一類基于極限序列核的大型裝備復雜系統多狀態可靠性快速評估算法。研究分析與案例仿真表明：

（1）算法建模合理、解算便捷、評估準確，能有效滿足大型裝備復雜系統的可靠性評估與風險預報要求；

（2）算法突破了傳統解析算法的大維度解算技術瓶頸，大幅度提升了大型裝備復雜系統多狀態可靠性的評估效率，工程應用潛能大；

（3）算法程式化特征明顯，計算資源要求低、計算過程耗時短，便于工程軟件的平臺開發與核心功能實現；

（4）算法適用范圍廣，串并、并串、冷儲備、表決等常見齊次和非齊次工程耦合結構，均可直接適用；

（5）算法解算彈性大，可滿足保守、樂觀等不同評估策略下的工程風險管控需求；

（6）算法豐富了復雜系統多狀態可靠性建模、分析與評估體系，促進了大型裝備復雜系統可靠性快速評估與風險預報技術發展。

下一步工作如下：

（1）探討非齊次耦合結構下大型裝備復雜系統極限序列核構建與極限逼近函數確定的通用方法；

（2）探討大型裝備復雜系統多狀態可靠性快速評估交互軟件開發內核與工程實現技術。