遠(yuǎn)程空空導(dǎo)彈角度約束增程彈道制導(dǎo)律研究

張喜豪，張金鵬, 沈 欣

(1. 中國(guó)空空導(dǎo)彈研究院，河南 洛陽(yáng) 471009； 2. 航空制導(dǎo)武器航空科技重點(diǎn)實(shí)驗(yàn)室，河南 洛陽(yáng) 471009; 3.空裝駐洛陽(yáng)地區(qū)第一軍事代表室，河南 洛陽(yáng) 471009)

0 引 言

增加射程是空空導(dǎo)彈不斷追求的一個(gè)方向，在有限尺寸重量約束下，研究如何提高空空導(dǎo)彈的攻擊距離具有重要的現(xiàn)實(shí)意義。除了從氣動(dòng)布局、 推力系統(tǒng)等方面進(jìn)行設(shè)計(jì)外，增程彈道規(guī)劃及其制導(dǎo)律技術(shù)也是實(shí)現(xiàn)增程的關(guān)鍵技術(shù)之一。彈道規(guī)劃及其制導(dǎo)律技術(shù)應(yīng)用的范圍比較廣泛，文獻(xiàn)[3]以無(wú)人機(jī)載空地導(dǎo)彈為對(duì)象，提出一種適應(yīng)復(fù)合制導(dǎo)的空地導(dǎo)彈的彈道規(guī)劃方法，提高無(wú)人機(jī)載空地導(dǎo)彈的發(fā)射距離。文獻(xiàn)[4]以高超聲速飛行器為對(duì)象，提出一種非連續(xù)點(diǎn)火助推方案，通過(guò)設(shè)計(jì)增大助推段射程，提高飛行器的射程。文獻(xiàn)[5]針對(duì)反輻射導(dǎo)彈被動(dòng)目標(biāo)定位問(wèn)題的關(guān)鍵技術(shù)研究，提出一種導(dǎo)彈可觀測(cè)性增強(qiáng)的彈道規(guī)劃方法，給出了典型非線性濾波器的選取分析。文獻(xiàn)[6]研究垂直發(fā)射的多導(dǎo)彈系統(tǒng)的高拋彈道協(xié)同制導(dǎo)律問(wèn)題，采用“初+中+末制導(dǎo)”的復(fù)合制導(dǎo)方式實(shí)現(xiàn)高拋彈道，設(shè)計(jì)中制導(dǎo)段協(xié)同導(dǎo)引律，減少協(xié)同攻擊網(wǎng)絡(luò)中各導(dǎo)彈的命中時(shí)間差。從彈道規(guī)劃技術(shù)的研究可以看出，其應(yīng)用與研究對(duì)象和研究目的密切相關(guān)。本文以空空導(dǎo)彈實(shí)現(xiàn)遠(yuǎn)程精確打擊為目的，提出一種適用于遠(yuǎn)程空空導(dǎo)彈的角度約束增程彈道規(guī)劃方案，重點(diǎn)研究中制導(dǎo)律，減少導(dǎo)彈飛行過(guò)程中的阻力，滿足中、 末制導(dǎo)交接班位置、 視線角和入射角等約束條件，達(dá)到改善彈道性能的效果。

1 角度約束增程彈道規(guī)劃方案以及制導(dǎo)律研究

遠(yuǎn)程空空導(dǎo)彈飛行距離遠(yuǎn)、 時(shí)間長(zhǎng)，多采用復(fù)合制導(dǎo)系統(tǒng)，典型的復(fù)合制導(dǎo)系統(tǒng)由數(shù)據(jù)鏈指令修正+捷聯(lián)式慣性中制導(dǎo)和主動(dòng)雷達(dá)末制導(dǎo)組成。數(shù)據(jù)鏈指令修正系統(tǒng)傳送載機(jī)測(cè)量的目標(biāo)信息，捷聯(lián)式慣性系統(tǒng)測(cè)量導(dǎo)彈信息，由飛控計(jì)算機(jī)將這些信息進(jìn)行綜合形成中制導(dǎo)控制指令，來(lái)控制導(dǎo)彈飛行，然后進(jìn)入中、 末制導(dǎo)交接班，以便截獲目標(biāo)。截獲目標(biāo)后用主動(dòng)雷達(dá)自尋的系統(tǒng)進(jìn)行末制導(dǎo)，直至摧毀目標(biāo)。復(fù)合制導(dǎo)系統(tǒng)可以充分發(fā)揮不同制導(dǎo)段中不同制導(dǎo)技術(shù)的優(yōu)勢(shì)，以滿足特定的制導(dǎo)需求。

本文在復(fù)合制導(dǎo)過(guò)程劃分的基礎(chǔ)上，將遠(yuǎn)程空空導(dǎo)彈角度約束增程彈道規(guī)劃為初始段、 爬高段、 成型段和末制導(dǎo)段。角度約束增程彈道規(guī)劃示意圖如圖1所示。初始段： 導(dǎo)彈和載機(jī)安全分離段，這里不做研究。爬高段： 利用大氣密度隨高度增加而降低的特性，導(dǎo)彈爬升到一定的高度，避開(kāi)低空稠密大氣而在阻力較小的稀薄大氣中飛行，減小飛行過(guò)程中空氣阻力。成型段： 將導(dǎo)彈制導(dǎo)到期望的中、 末交接班區(qū)域，并滿足期望的視線角和入射角約束。這里的入射角約束，是約束導(dǎo)引頭雷達(dá)天線照射目標(biāo)所發(fā)射的入射波與地面的夾角，入射角近似取彈道傾角的絕對(duì)值。末制導(dǎo)段： 導(dǎo)彈在完成中、 末制導(dǎo)交接班后進(jìn)入末制導(dǎo)。爬高段、 成型段和末制導(dǎo)段側(cè)向平面均采用最優(yōu)制導(dǎo)律，下面根據(jù)不同飛行段的需求，研究各階段縱向平面相關(guān)制導(dǎo)律實(shí)現(xiàn)問(wèn)題。

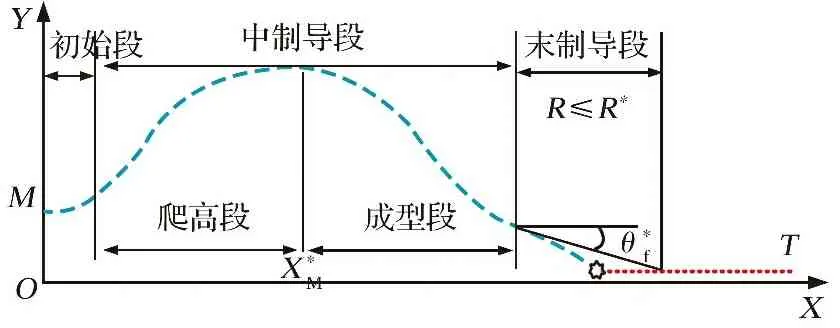
圖1 角度約束增程彈道規(guī)劃示意圖

1.1 爬高增程制導(dǎo)律

爬高增程制導(dǎo)律采用過(guò)載指令控制，控制爬高段的過(guò)載和持續(xù)時(shí)間，實(shí)現(xiàn)中制導(dǎo)階段導(dǎo)彈的爬高。在文獻(xiàn)[12]中EET-2算法的基礎(chǔ)上進(jìn)行改進(jìn)，考慮導(dǎo)彈當(dāng)前速度與爬升彈道傾角、 爬升高度的關(guān)系，引入速度項(xiàng)對(duì)爬高算法進(jìn)行修正和約束控制，爬高增程制導(dǎo)律為

=(-)-+·cos

(1)

式中：為爬升最佳高度；為導(dǎo)彈當(dāng)前高度；為導(dǎo)彈當(dāng)前速度；為當(dāng)前彈道傾角；為重力加速度。

由式(1)可得，爬升段的彈道傾角變化率為

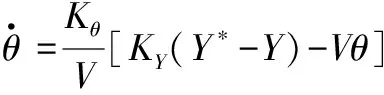
(2)

式中：-為期望高度與當(dāng)前高度的差值，當(dāng)前高度離期望高度越遠(yuǎn)，爬升越快；可以近似看作當(dāng)前狀態(tài)高度的可變化量，將此項(xiàng)作為修正項(xiàng)。若當(dāng)前爬升角較大，此時(shí)不宜拉大過(guò)載，修正項(xiàng)使得爬升速率降低。爬高彈道通常初始爬升率較大然后逐漸減小，在達(dá)到期望高度取到最小值，爬高過(guò)程平穩(wěn)。

1.2 成型角度約束制導(dǎo)律

在中制導(dǎo)結(jié)束時(shí)，導(dǎo)彈的位置、 速度以及航向等條件應(yīng)滿足中、 末制導(dǎo)交接班的要求。如果一直處于爬高段，則很難達(dá)到交接班要求。此外，在打擊超低空目標(biāo)時(shí)，地海雜波會(huì)導(dǎo)致雷達(dá)導(dǎo)引頭測(cè)量精度下降。研究表明，當(dāng)導(dǎo)引頭入射波以布魯斯特角入射時(shí)，地海雜波的反射系數(shù)最小。布魯斯特角在山地、 平原、 海洋等情況下是不同的，一般在10°～25°之間。因此，角度約束具有重要意義，故研究成型角度約束制導(dǎo)律，把中、 末制導(dǎo)交接班點(diǎn)看作虛擬目標(biāo)點(diǎn)，將導(dǎo)彈制導(dǎo)到虛擬目標(biāo)點(diǎn)附近，達(dá)到期望的視線角和入射角。

導(dǎo)彈和交接班點(diǎn)相對(duì)關(guān)系如圖2所示。圖中，為導(dǎo)彈加速度；為導(dǎo)彈到虛擬目標(biāo)點(diǎn)的距離；為導(dǎo)彈當(dāng)前速度矢量和期望末速度矢量之間的角度；為當(dāng)前速度矢量和導(dǎo)彈與虛擬目標(biāo)視線之間的角度。

交接班點(diǎn)位置計(jì)算：

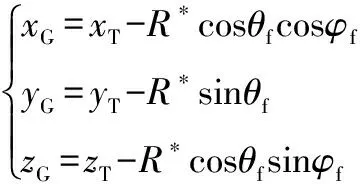
(3)

式中： (,,)為目標(biāo)位置信息；,分別為導(dǎo)彈期望的末端傾角和偏角；為制導(dǎo)頭截獲距離。

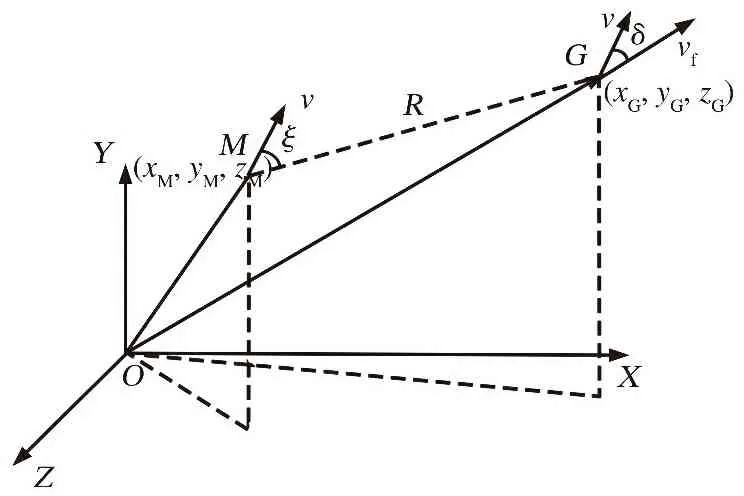
圖2 導(dǎo)彈與交接班點(diǎn)相對(duì)關(guān)系

,分別為導(dǎo)彈與交接班點(diǎn)(虛擬目標(biāo))距離和相對(duì)速度，設(shè)相對(duì)加速度為控制量，則系統(tǒng)狀態(tài)方程為

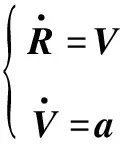
(4)

初始條件為

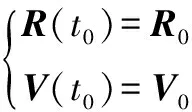
(5)

在此制導(dǎo)律設(shè)計(jì)中，期望整個(gè)飛行過(guò)程能量最省，并且末端彈目相對(duì)速度矢量()與末端相對(duì)位置矢量()滿足指定要求。

采用最優(yōu)控制理論得到滿足末端邊界條件的制導(dǎo)律。用軟懲罰實(shí)現(xiàn)在制導(dǎo)律設(shè)計(jì)中終端邊界條件相對(duì)重要性的權(quán)衡。將此問(wèn)題的軟懲罰定義為

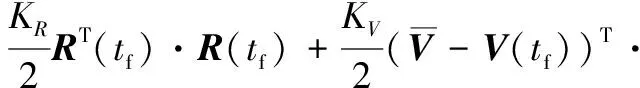
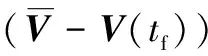
(6)

式中：和為常數(shù)，為末端導(dǎo)彈位置與預(yù)測(cè)交接班點(diǎn)的偏差的權(quán)重，為末端相對(duì)速度矢量與所需的終端速度矢量之前的偏差的權(quán)重。

此最優(yōu)控制問(wèn)題性能指標(biāo)可以描述為

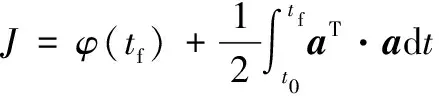
(7)

取此問(wèn)題的哈密頓函數(shù)為

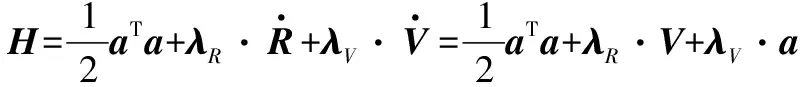
(8)

式中：和為伴隨向量。

由最優(yōu)控制理論可知，有協(xié)態(tài)方程：

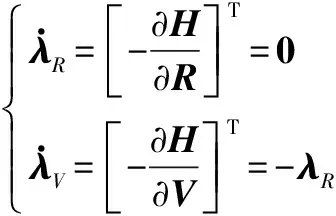
(9)

且伴隨向量滿足：

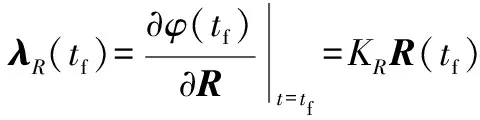
(10)

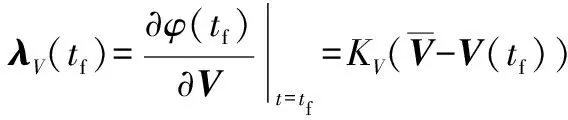
(11)

將式(11)代入式(9)積分，聯(lián)立式(10)，可得

()(-)

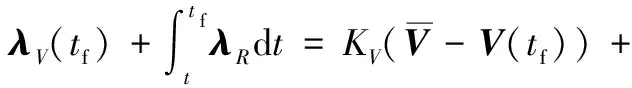
(12)

由最優(yōu)控制理論的極值條件可知，這里考慮無(wú)約束，則有取最小值的必要條件：

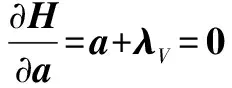
(13)

將式(12) 代入式(13)，可得最優(yōu)開(kāi)環(huán)控制：

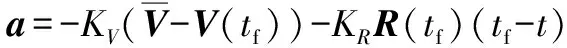
(14)

由相對(duì)運(yùn)動(dòng)方程可知：

(15)

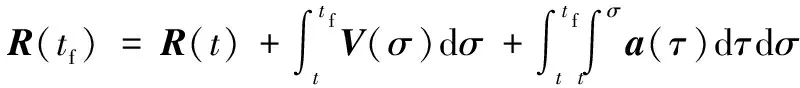
(16)

設(shè)零控脫靶量為

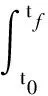
(17)

式中：=-，為剩余飛行時(shí)間。

將式(14)代入式(15)積分，與式(17)聯(lián)立，有

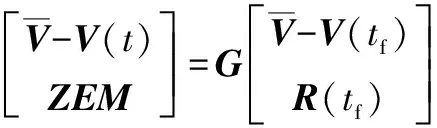
(18)

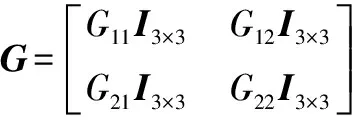
(19)

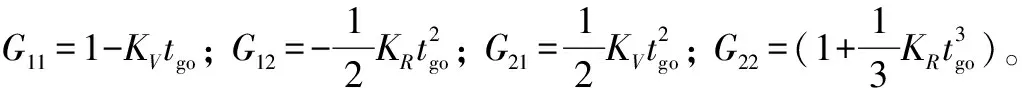
將式(18)求逆，有

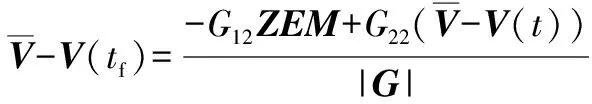
(20)

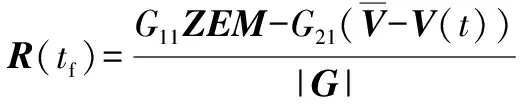
(21)

將式(20)～(21)代入式(14)可得閉環(huán)最優(yōu)控制：

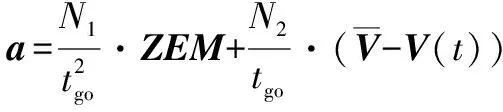
(22)

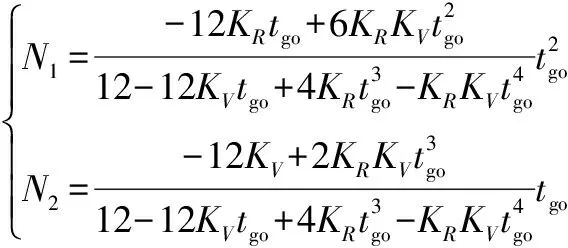
(23)

當(dāng)取和趨于無(wú)窮大，注意到

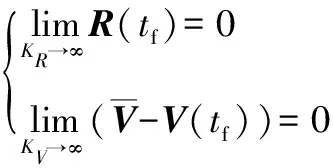
(24)

則有

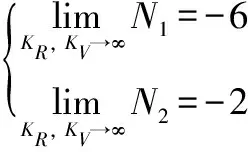
(25)

假設(shè)目標(biāo)加速度為0，結(jié)合圖2所示的相對(duì)運(yùn)動(dòng)關(guān)系，則可以將式(22)矢量方程轉(zhuǎn)化為標(biāo)量方程：

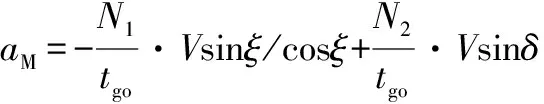
(26)

式中：為法向加速度。

將法向加速度投影到縱向平面, 同時(shí)將式(26)中用/替換，可得成型角度約束制導(dǎo)律：

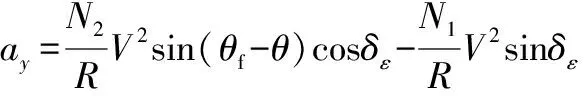
(27)

式中：為法向加速度在縱向平面的投影；為當(dāng)前位置與交接班點(diǎn)的距離；為導(dǎo)彈期望末速度方向；為相對(duì)距離矢量與導(dǎo)彈當(dāng)前速度矢量的夾角在縱向平面的投影。

1.3 末制導(dǎo)律

末制導(dǎo)采用最優(yōu)制導(dǎo)律，由導(dǎo)引頭提供目標(biāo)信息，縱向平面的制導(dǎo)律為

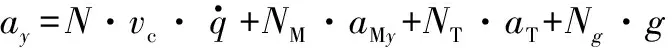
(28)

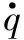
1.4 制導(dǎo)指令交接算法

采用復(fù)合制導(dǎo)律設(shè)計(jì)，各飛行段制導(dǎo)律不同，需要考慮制導(dǎo)指令交接問(wèn)題。在交接時(shí)，開(kāi)始以前一段加速度指令為主，主導(dǎo)成分逐漸減弱； 然后以后一段加速度指令為主，逐漸增強(qiáng)。優(yōu)選交接算法如下：

()=2()+[1()-2()]()

(29)

()=(′+-)′，∈[，+′]

(30)

式中：()為交接段加速度指令；1()為前一段制導(dǎo)律在時(shí)刻的加速度指令；2()為后一段制導(dǎo)律在時(shí)刻的加速度指令；()為一個(gè)調(diào)節(jié)比重的時(shí)變系數(shù)；為交接段開(kāi)始時(shí)間；′為交接段持續(xù)時(shí)間。

1.5 制導(dǎo)律參數(shù)優(yōu)化

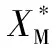
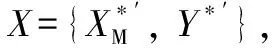
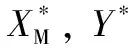
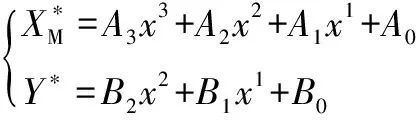
(31)

式中：(=0, 1, 2, 3)和(=0, 1, 2)為多項(xiàng)式擬合得到的系數(shù)；為發(fā)射距離。

在實(shí)際應(yīng)用中，可以根據(jù)不同的發(fā)射條件通過(guò)式(31)獲得當(dāng)前情況下近似最優(yōu)的參數(shù)，實(shí)現(xiàn)增程彈道。

2 仿真驗(yàn)證

以表1中的典型發(fā)射條件為例，進(jìn)行仿真驗(yàn)證，將本文提出的角度約束增程彈道與常規(guī)彈道性能對(duì)比，常規(guī)彈道全程采用最優(yōu)制導(dǎo)律。

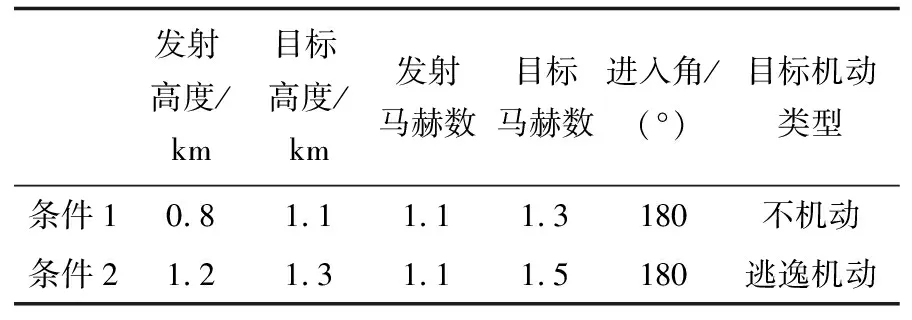
表1 仿真條件

2.1 仿真結(jié)果1

在條件1下，針對(duì)勻速運(yùn)動(dòng)目標(biāo)，在不同發(fā)射距離條件下，采用粒子群優(yōu)化算法，得到的優(yōu)化彈道如圖3所示，對(duì)應(yīng)的最優(yōu)參數(shù)如表2所示。要求中制導(dǎo)末端彈道傾角約束-10°，彈目距離小于20 km，視為中制導(dǎo)結(jié)束，進(jìn)入末制導(dǎo)階段。其中雙脈沖型發(fā)動(dòng)機(jī)第一級(jí)和第二級(jí)點(diǎn)火間隔時(shí)間為12 s，=013,=004。

圖3 不同發(fā)射距離對(duì)應(yīng)的優(yōu)化彈道

表2 不同發(fā)射距離對(duì)應(yīng)的最優(yōu)參數(shù)

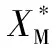
2.2 仿真結(jié)果2

在條件1下，針對(duì)勻速運(yùn)動(dòng)目標(biāo)，發(fā)射距離70 km，要求中制導(dǎo)末端彈道傾角約束-10°，彈目距離小于20 km，視為中制導(dǎo)結(jié)束，進(jìn)入末制導(dǎo)階段。增程彈道爬高段制導(dǎo)律參數(shù)：=013，=004，結(jié)果如圖4(a)～(d)所示。增程彈道和常規(guī)彈道在仿真時(shí)，都采用雙脈沖型發(fā)動(dòng)機(jī)，其中第一級(jí)和第二級(jí)點(diǎn)火間隔時(shí)間為12 s，速度變化對(duì)比如圖4(c)所示。增程彈道在第一級(jí)脈沖工作階段，導(dǎo)彈通過(guò)爬高將動(dòng)能轉(zhuǎn)化為勢(shì)能儲(chǔ)存，飛行速度顯著降低； 當(dāng)?shù)诙?jí)脈沖工作時(shí)，導(dǎo)彈已飛到約6 km，此時(shí)點(diǎn)火可以獲得更大的速度增量，相較常規(guī)彈道，減少了在低空加速飛行期間空氣阻力引起的能量損失。

圖4 增程彈道與常規(guī)彈道性能對(duì)比

圖4(a)中點(diǎn)劃線部分為中制導(dǎo)結(jié)束時(shí)導(dǎo)彈位置與目標(biāo)位置的連線。由圖4(b)可知，增程彈道雖然在飛行距離小于2 km時(shí)阻力較大，但是通過(guò)優(yōu)化彈道，增大飛行高度，減少了中間段的阻力。從表3對(duì)比結(jié)果中可以看出，相較于常規(guī)彈道，增程彈道末速增加19.19%，增程彈道爬升高度更高，飛行距離更遠(yuǎn)，平均速度更大，達(dá)到了改善彈道性能指標(biāo)的效果。

2.3 仿真結(jié)果3

在條件2下，目標(biāo)逃逸機(jī)動(dòng)，加速度9.8 m/s，末速不小于350 m/s，最遠(yuǎn)距離增程彈道與最遠(yuǎn)距離常規(guī)彈道對(duì)比結(jié)果如圖5所示。其中： 末制導(dǎo)距離20 km，彈道傾角約束-10°，雙脈沖型發(fā)動(dòng)機(jī)第一級(jí)和第二級(jí)點(diǎn)火間隔時(shí)間為20 s。

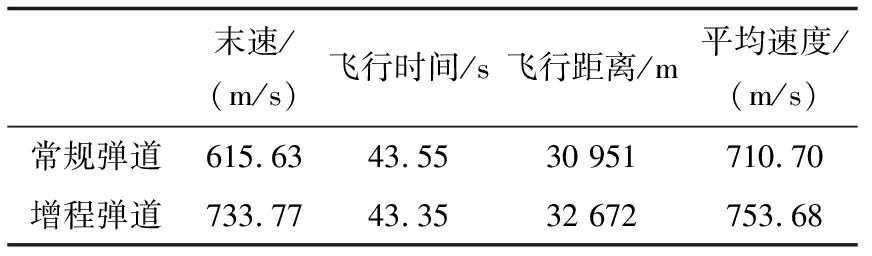
表3 中制導(dǎo)階段對(duì)比

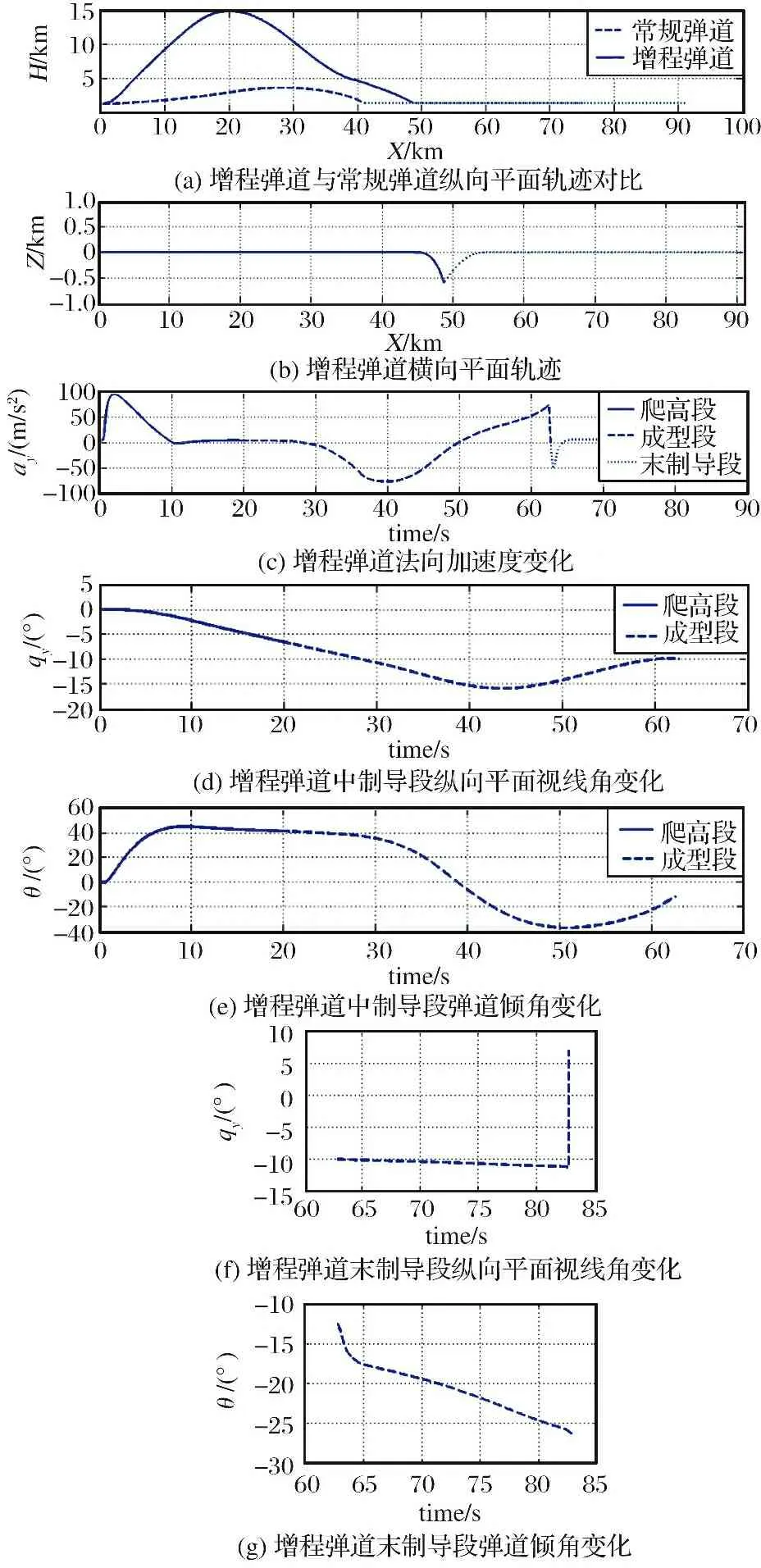
圖5 條件2下的最遠(yuǎn)射程彈道

從加速度變化曲線圖5(c)中可以看出，增程彈道在爬高段和成型段，導(dǎo)彈的需用過(guò)載較大，最大值不超過(guò)98 m/s。增程彈道中、 末制導(dǎo)交接時(shí)縱向平面視線角為-10.02°，入射角為12.18°，在末制導(dǎo)階段視線角變化范圍在-10.02°～-11.33°之間，脫靶量為0.401 m。驗(yàn)證了通過(guò)設(shè)計(jì)成型段彈道，中、 末制導(dǎo)交接時(shí)，視線角和入射角能達(dá)到約束要求。規(guī)劃成型段彈道還可使得末制導(dǎo)階段視線角的變化范圍比較小，有利于中、 末制導(dǎo)交接班導(dǎo)引頭截獲目標(biāo)和末制導(dǎo)階段穩(wěn)定跟蹤。

在不同的發(fā)射條件下，末速不小于350 m/s，增程彈道和常規(guī)彈道能夠達(dá)到的最遠(yuǎn)距離對(duì)比結(jié)果如表4所示。可以看出，所提出的增程彈道及其制導(dǎo)律，相對(duì)常規(guī)彈道及其制導(dǎo)律，增程效果明顯。

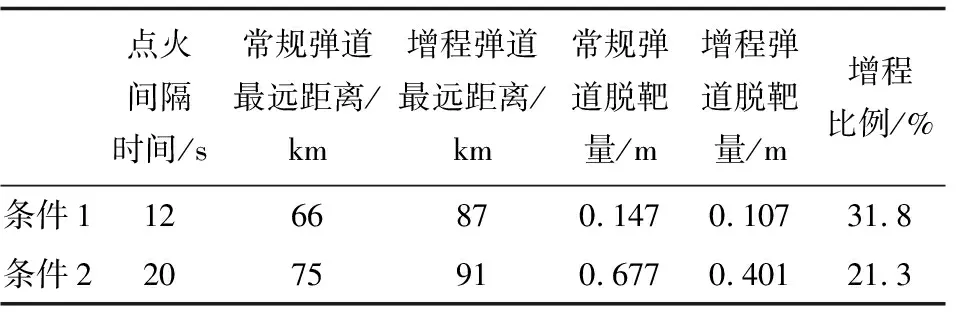
表4 不同條件下的增程效果

3 結(jié) 論

本文所提出的對(duì)角度約束增程彈道分段規(guī)劃方案，將復(fù)雜的難以求解析解的角度約束增程彈道制導(dǎo)律問(wèn)題轉(zhuǎn)化為多段復(fù)合制導(dǎo)律問(wèn)題，研究滿足不同飛行段要求的制導(dǎo)律，達(dá)到實(shí)現(xiàn)增程兼角度約束的綜合最優(yōu)。角度約束增程制導(dǎo)律結(jié)構(gòu)簡(jiǎn)單，彈目制導(dǎo)信息能夠獲取或估計(jì)，便于工程實(shí)現(xiàn)； 爬高段彈道顯著提高了導(dǎo)彈的最大末速和平均速度，對(duì)實(shí)現(xiàn)增程效果明顯； 成型段彈道能夠?qū)崿F(xiàn)中、 末制導(dǎo)交接班視線角和入射角等約束。所提出的思路和方法對(duì)其他戰(zhàn)術(shù)導(dǎo)彈增程彈道技術(shù)的研究也有理論和工程參考價(jià)值。實(shí)際作戰(zhàn)過(guò)程中，戰(zhàn)場(chǎng)態(tài)勢(shì)更復(fù)雜，因此，需要進(jìn)一步研究導(dǎo)彈離軸發(fā)射和不同進(jìn)入角等情況對(duì)增程彈道的影響。