基于Q學(xué)習(xí)模型的無信號交叉口離散車隊(duì)控制*

錢立軍，陳 晨，陳 健，陳欣宇，熊 馳

（1.合肥工業(yè)大學(xué)汽車與交通工程學(xué)院，合肥230009；2.南昌理工學(xué)院機(jī)電工程學(xué)院，南昌330044）

前言

當(dāng)前，各國主要大型城市已建立為自動(dòng)駕駛服務(wù)的高智能化基礎(chǔ)設(shè)施，并開展了車輛位置實(shí)時(shí)采集、低時(shí)延通信等功能測試。自動(dòng)駕駛汽車為主體的無信號燈交叉口自動(dòng)管理策略已成為一個(gè)研究熱點(diǎn)。

離散的分布式控制是一類有效的車輛控制策略，能分?jǐn)偪刂破鞯挠?jì)算負(fù)荷。此時(shí)，各車擁有單獨(dú)的控制器，能夠識別相鄰車的運(yùn)動(dòng)并協(xié)商通行權(quán)。為了降低控制算法的復(fù)雜度，可根據(jù)不同的行駛?cè)蝿?wù)對交叉口的物理空間進(jìn)行劃分。一般地，車輛在無信號燈交叉口的任務(wù)被分解為：狀態(tài)觀察、到達(dá)時(shí)間優(yōu)化和軌跡跟蹤控制。由于離散化程度越高的分布式方法擁有更好的實(shí)時(shí)性，則將最小控制單元轉(zhuǎn)化為車隊(duì)可以有效減少控制對象的數(shù)量。

在提升交通性能方面，車隊(duì)已被證明具有足夠的應(yīng)用潛力，并在高速場景中得到驗(yàn)證。但是，大部分擁堵和事故發(fā)生于交通瓶頸處，在非高速場景驗(yàn)證車隊(duì)的優(yōu)勢也十分必要。一方面，運(yùn)動(dòng)趨勢相同的車輛在進(jìn)行組隊(duì)時(shí)，可以減少通信開銷。另一方面，在自適應(yīng)巡航等自組織策略中，適當(dāng)規(guī)模的車隊(duì)將會(huì)使道路通行能力得到成倍提升。此外，車隊(duì)可使信號燈交叉口的交通性能指標(biāo)得到優(yōu)化。

然而，固定規(guī)模的車隊(duì)無法適應(yīng)不同密度的車流環(huán)境。考慮到城市場景中車流量的不確定性，無信號燈交叉口環(huán)境下需要更為靈活的組隊(duì)策略。另外，受限于基礎(chǔ)設(shè)施的范圍和帶寬，隊(duì)形調(diào)整的時(shí)間和空間并不充裕。因此，研究快捷且智能的隊(duì)形選擇系統(tǒng)來應(yīng)對復(fù)雜的城市交通環(huán)境有一定必要性。

近年來，強(qiáng)化學(xué)習(xí)（reinforcement learning，RL）因其適應(yīng)性強(qiáng)的特點(diǎn)在交通領(lǐng)域得到深入研究。除了調(diào)控信號燈配時(shí)之外，RL也逐漸被應(yīng)用于車輛的視覺學(xué)習(xí)、轉(zhuǎn)向控制、運(yùn)動(dòng)規(guī)劃等方面。考慮到車輛的動(dòng)力學(xué)特性具有馬爾科夫性，可使用無模型的RL方法來求解部分可觀測的馬爾科夫決策過程。但是，信號燈周期仍然是當(dāng)前智能體學(xué)習(xí)過程中不可缺失的參數(shù)之一，而RL在無信號燈交叉口的研究并不充分。

為此，本文在基于Q學(xué)習(xí)的組隊(duì)決策過程中結(jié)合固定時(shí)距跟車模型，提出一種基于多車隊(duì)協(xié)同規(guī)劃的交通流離散策略，設(shè)計(jì)了包含車隊(duì)選型與車輛軌跡規(guī)劃的計(jì)算框架。并且，結(jié)合了基于車隊(duì)的交通流模型和多車隊(duì)協(xié)同策略，定義了一個(gè)車隊(duì)通行時(shí)間的安全約束。

其次，考慮到車隊(duì)組合中的狀態(tài)變量有限，選擇高效的Q學(xué)習(xí)方法進(jìn)行建模，設(shè)計(jì)獎(jiǎng)勵(lì)函數(shù)的同時(shí)考慮了通行效率、行車延誤和燃油經(jīng)濟(jì)性等指標(biāo)。并且，根據(jù)交叉口功能區(qū)間定義了初始狀態(tài)和動(dòng)作空間，用于確定車隊(duì)組合狀態(tài)。

最后，在建立多車隊(duì)協(xié)同最優(yōu)控制問題時(shí)，設(shè)計(jì)了一個(gè)預(yù)防追尾碰撞的安全約束。基于高斯偽譜法對合流區(qū)內(nèi)的車隊(duì)軌跡進(jìn)行預(yù)求解。通過仿真試驗(yàn)，分析了所提策略有效性和車隊(duì)協(xié)同的優(yōu)勢。

1 問題描述與建模

在智能交通環(huán)境下，道路專用短程通信技術(shù)（dedicated short range communication，DSRC）覆蓋范圍內(nèi)的交叉口路網(wǎng)可被劃分為緩沖區(qū)、核心區(qū)和自由駕駛區(qū)。本文聚焦于孤立交叉口，根據(jù)文獻(xiàn)［14］選擇一個(gè)典型的單車道十字路口為研究場景。交叉口中的觀察區(qū)、協(xié)同區(qū)和合流區(qū)分別對應(yīng)于路網(wǎng)中的功能區(qū)間，如圖1所示。、和分別表示觀察區(qū)、協(xié)同區(qū)和合流區(qū)的長度尺寸，為車道寬度。

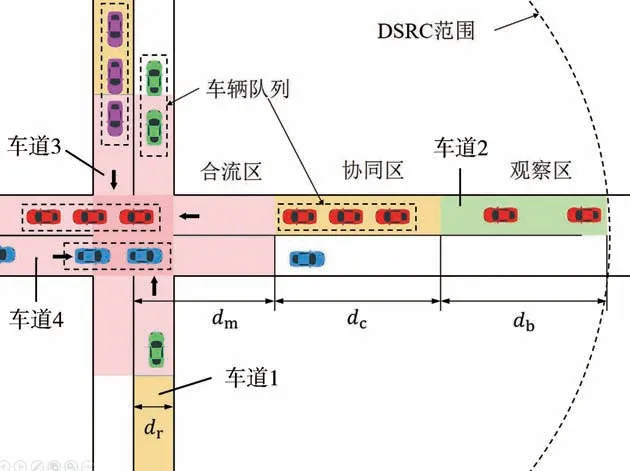
圖1 交叉口功能區(qū)間示意圖

1.1 交通流離散控制框架

在以車隊(duì)為通行單元的要求下，以任意車輛為例來說明其組合分配、隊(duì)形排列和通過路口的過程。其中，以交叉口中心點(diǎn)為原點(diǎn)，車道上第輛車的位置記為x。該車輛駛過交叉口過程中須經(jīng)歷以下4個(gè)步驟。

步驟1：位置觀察階段。首先，車輛位于觀察區(qū)以外，X表示所有在觀察區(qū)內(nèi)車輛位置的集合。當(dāng)該車進(jìn)入觀察區(qū)后（x≤++），其位置、速度和加速度等信息被路側(cè)單元所識別。識別到的車輛會(huì)被添加進(jìn)集合中，即X=X∪x。

步驟2：組合分配階段。定義同時(shí)間段內(nèi)協(xié)同通過交叉口的車隊(duì)集合為一個(gè)組合。在協(xié)同區(qū)內(nèi)，將采用Q學(xué)習(xí)方法，于X中選擇最優(yōu)的車隊(duì)規(guī)模。當(dāng)有車輛到達(dá)協(xié)同區(qū)時(shí)（x=+），建立Q學(xué)習(xí)的可用狀態(tài)空間。基于所建立的獎(jiǎng)勵(lì)函數(shù)和約束條件，選擇當(dāng)前情況下的最優(yōu)組合狀態(tài)=(，，，)。

步驟3：車隊(duì)排列階段。此步驟同樣發(fā)生在協(xié)同區(qū)內(nèi)。根據(jù)得到的最優(yōu)車隊(duì)規(guī)模，各車道上的車輛將受到以下控制：（1）各車道上位置最靠前的車輛被定義為領(lǐng)航車，其他車輛為跟隨車，且所有的領(lǐng)航車將同時(shí)到達(dá)合流區(qū)，即x()=；（2）跟隨車將在時(shí)刻之前，與其領(lǐng)航車排列成標(biāo)準(zhǔn)車隊(duì)。被選中的車輛也將從X中被剔除。

步驟4：軌跡跟蹤階段。文獻(xiàn)［15］表明，可通過尋找離線的運(yùn)動(dòng)方案來提高協(xié)同運(yùn)動(dòng)的實(shí)時(shí)性。基于此，在時(shí)刻之后，所有的車隊(duì)將在合流區(qū)內(nèi)跟蹤事先儲存的安全軌跡，直至其通過交叉口。此交通流離散控制框架如圖2所示。

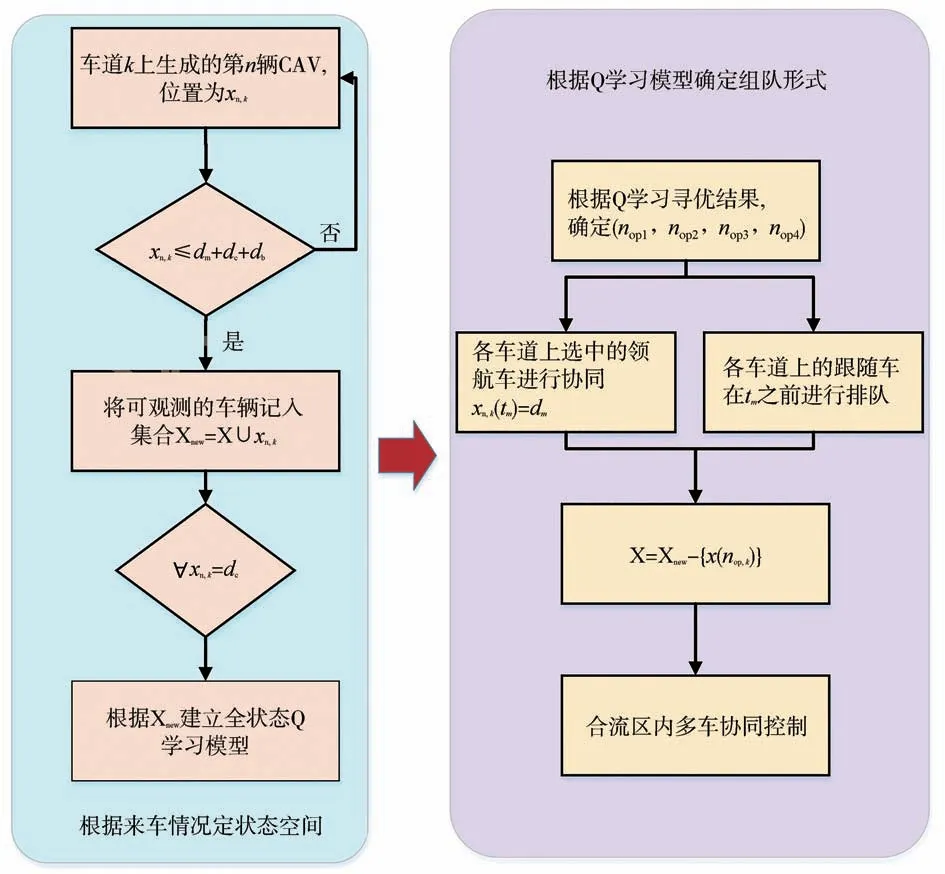
圖2 離散控制框架流程圖

經(jīng)過上述步驟，各車道上連續(xù)的交通流被拆分為多個(gè)小規(guī)模車隊(duì)，并在不同時(shí)間段內(nèi)受到分布式控制。

1.2 車隊(duì)離散模型

對于車道上規(guī)模為n∈Ν的車隊(duì)，其領(lǐng)航車的運(yùn)動(dòng)學(xué)模型為

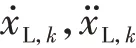
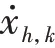
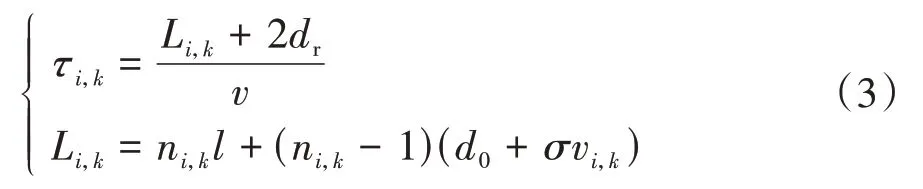
式中：L為車隊(duì)總長度；v為車隊(duì)通過交叉口的平均速度。虛擬車隊(duì)如圖3所示，圖中藍(lán)色箭頭形象描述虛擬車隊(duì)的構(gòu)造。當(dāng)多個(gè)車隊(duì)形成的組合進(jìn)入交叉口時(shí)，有沖突隱患的車隊(duì)可以被視為虛擬隊(duì)列，該虛擬車隊(duì)被定義為一個(gè)組合。假設(shè)各車隊(duì)在交叉口處的平均速度均為常數(shù)，則此組合的交叉口占用時(shí)間為

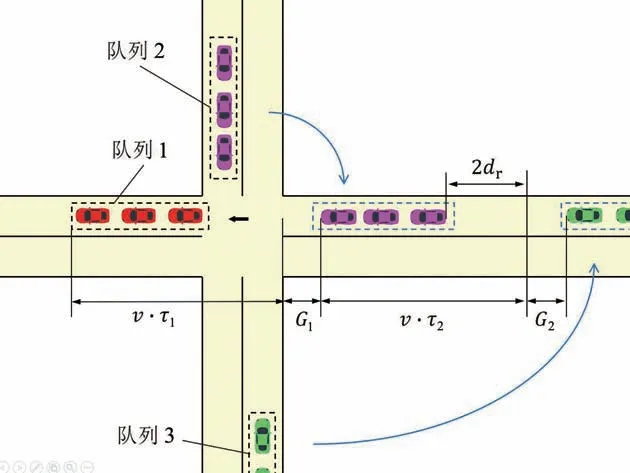
圖3 虛擬車隊(duì)與間隙

式中：表示此組合的時(shí)間窗口；表示在該組合中包含的車隊(duì)數(shù)目；τ為此組合中第個(gè)車隊(duì)在交叉口的占有時(shí)間；G表示組合中兩個(gè)車隊(duì)之間的排隊(duì)間隙與交叉口尺寸的差值，表示這些差值的總和。基于此，交叉口的瞬時(shí)吞吐量（輛/h）為

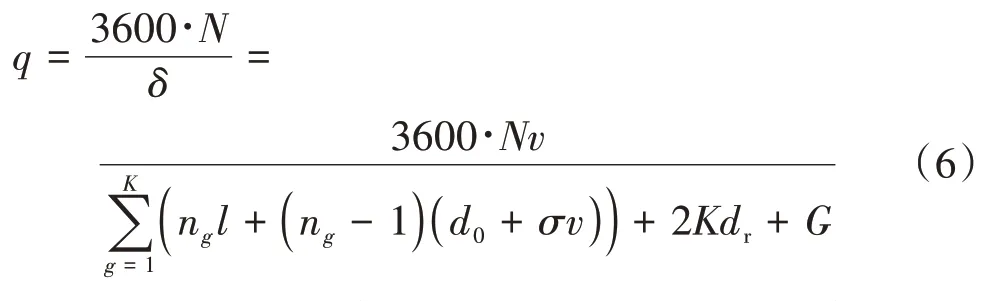
式中：表示該組合中的車輛總數(shù)；n表示第個(gè)車隊(duì)的規(guī)模。以為自變量對求偏導(dǎo)，可得

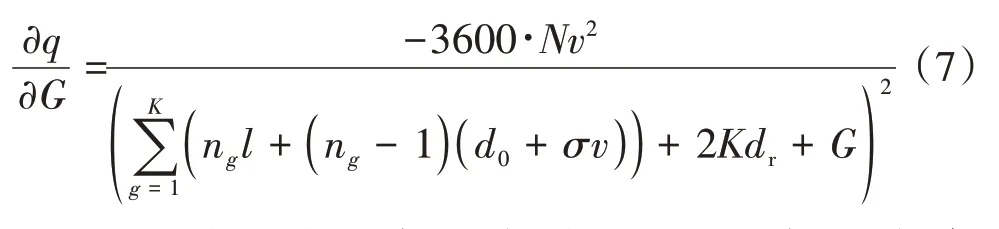
由于式（7）恒為負(fù)，可知減少虛擬間隙是提高瞬時(shí)吞吐量的有效途徑。并且，圖3和式（7）展示了以下規(guī)律：對任何控制策略，=0時(shí)，控制效果與虛擬隊(duì)列的最優(yōu)效果相當(dāng)；＞0時(shí)，過大的車隊(duì)間隙會(huì)增大交叉口的占用時(shí)間；當(dāng)＜0時(shí)，將優(yōu)于虛擬隊(duì)列的控制效果。因此，在選擇組合形式時(shí)，定義一個(gè)強(qiáng)制性約束：

2 車隊(duì)組合分配

根據(jù)步驟2所定義，在協(xié)同區(qū)內(nèi)的車輛將根據(jù)集合X來選擇最優(yōu)的組合形式。由此，無信號燈交叉口的車隊(duì)協(xié)同通行問題被轉(zhuǎn)化為車隊(duì)間的組合問題。由于在通信范圍限制下車隊(duì)組合形式有限，故選擇Q學(xué)習(xí)算法對車隊(duì)組合情況進(jìn)行尋優(yōu)。

在協(xié)同區(qū)中，轉(zhuǎn)化后的強(qiáng)化學(xué)習(xí)問題為一個(gè)無模型的Markov決策過程。在每個(gè)時(shí)刻，一個(gè)動(dòng)作a∈將有的概率使環(huán)境狀態(tài)s∈轉(zhuǎn)變?yōu)樾碌臓顟B(tài)s。在狀態(tài)s下的動(dòng)作a將獲得一個(gè)價(jià)值r∈。Q學(xué)習(xí)方法中的價(jià)值迭代公式為

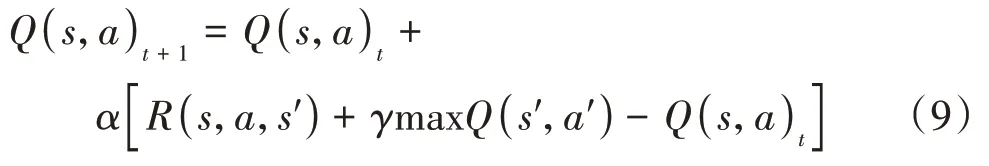
式中：∈(0，1)為學(xué)習(xí)率；∈(0，1)為系統(tǒng)折扣因子。

2.1 狀態(tài)向量設(shè)計(jì)

對于車隊(duì)而言，車速、跟車間距、規(guī)模等是影響其運(yùn)動(dòng)狀態(tài)的重要參數(shù)。在尺寸受限的場景中，車隊(duì)規(guī)模的影響高于其他參數(shù)。尤其在失去信號燈控制的平面交叉口，過大的車隊(duì)規(guī)模將延誤其他車輛。因此，將狀態(tài)空間定義為車隊(duì)規(guī)模的組合情況。對于四向單車道交叉口而言，狀態(tài)向量由4個(gè)元素組成=(，，，)∈S，其中n表示在此組合中第車道上的車隊(duì)規(guī)模。

基于此，在所研究的固定場景中，狀態(tài)量的總數(shù)為

式中表示單一車隊(duì)中的車輛數(shù)目上限。

2.2 動(dòng)作空間設(shè)計(jì)

由于狀態(tài)向量是車隊(duì)的組合類型，所以智能體的動(dòng)作是篩選一個(gè)合適的車隊(duì)組合。為了滿足狀態(tài)向量之間的切換條件，定義動(dòng)作為

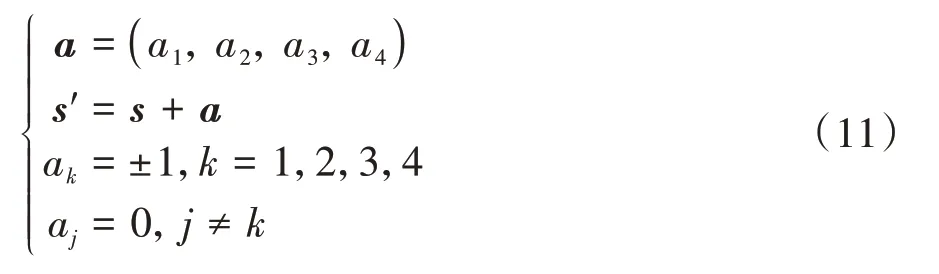
式中a表示該組合中位于車道上車隊(duì)的規(guī)模增減，且每次變動(dòng)的車輛數(shù)目為一輛。并且，狀態(tài)轉(zhuǎn)移過程中必須滿足邊界約束：

然而，在實(shí)際計(jì)算中并不是所有動(dòng)作都是可行的。因此，可使'滿足式（8）且'?X時(shí)的定義為一個(gè)有效動(dòng)作。

2.3 獎(jiǎng)勵(lì)函數(shù)設(shè)計(jì)

通行效率和行車延誤等參數(shù)是最能反映控制策略有效性的指標(biāo)。為了提高交叉口流量上限并降低延誤，在設(shè)計(jì)獎(jiǎng)勵(lì)函數(shù)時(shí)同時(shí)考慮了~4個(gè)指標(biāo)。

表示各狀態(tài)下在合流區(qū)內(nèi)呈現(xiàn)的瞬時(shí)效率。

表示車輛平均等待時(shí)間：

式中ε為各車隊(duì)的行車延誤。

為各車隊(duì)的行程時(shí)間標(biāo)準(zhǔn)差（standard deviation of travel time，SDTT）：

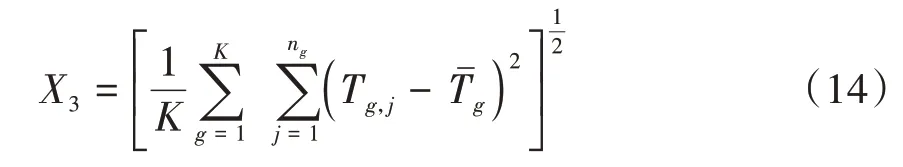
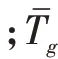
為合流區(qū)內(nèi)的平均燃油消耗（L/100 km）：

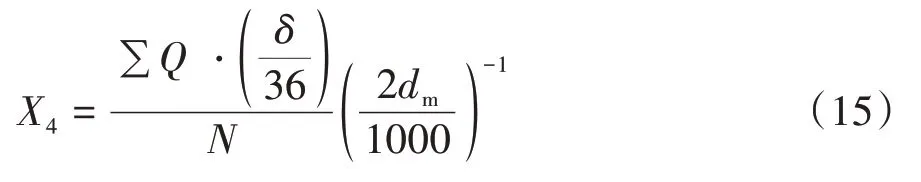
式中為車輛的平均瞬時(shí)油耗，L/h。

明確評價(jià)指標(biāo)之后，狀態(tài)下的獎(jiǎng)勵(lì)值定義為

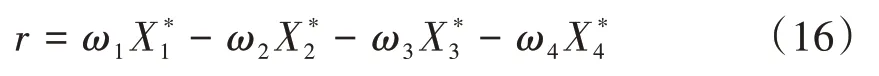
式中：X為對各指標(biāo)的樣本標(biāo)準(zhǔn)化處理后的值；、、和表示權(quán)重系數(shù)，且∑||=1；負(fù)號表示該指標(biāo)值呈負(fù)相關(guān)關(guān)系。

對于大流量的城市交叉口而言，減少擁堵是首要目標(biāo)。因此，瞬時(shí)效率的重要程度要遠(yuǎn)高于其他指標(biāo)。由于權(quán)重賦值過程具有強(qiáng)烈的主觀性，采用G1法對評價(jià)指標(biāo)進(jìn)行重要度排序，并確定權(quán)重系數(shù)的具體數(shù)值。

2.4 初始狀態(tài)設(shè)計(jì)

在確定可行動(dòng)作空間和獎(jiǎng)勵(lì)值之后，需對狀態(tài)的尋優(yōu)過程設(shè)計(jì)一個(gè)初始值。類似于二維路徑規(guī)劃的過程，從不同初始點(diǎn)出發(fā)找到的運(yùn)動(dòng)路徑也是不同的。在觀察區(qū)的尾部定義一個(gè)尺寸為的子區(qū)間，如圖4所示。該子區(qū)間只用于確定初始狀態(tài)，對其他過程不產(chǎn)生干擾。

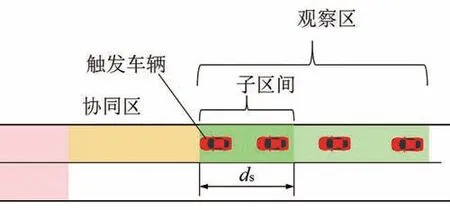
圖4 子區(qū)間示意圖

此時(shí)，智能體初始狀態(tài)被定義為

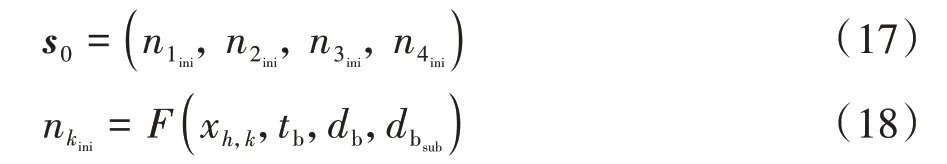
式中：n為車道上被選入初始狀態(tài)的車輛數(shù)目；(?)表 示 在 時(shí) 刻中，滿 足x()∈[+，++]的x的個(gè)數(shù)。當(dāng)有車輛到達(dá)協(xié)同區(qū)的時(shí)刻，將觸發(fā)和n的計(jì)算流程。并且，首個(gè)到達(dá)協(xié)同區(qū)的車輛被定義為觸發(fā)車輛。例如，圖4所示車道上的n=2。因此，由式（11）可知Q學(xué)習(xí)模型中狀態(tài)的變化過程為

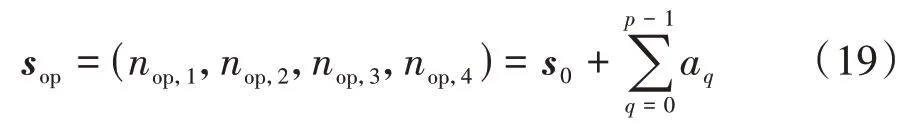
式中：為最優(yōu)狀態(tài)；為最優(yōu)狀態(tài)下位于第車道上的車隊(duì)規(guī)模；表示學(xué)習(xí)步數(shù)；表示Q學(xué)習(xí)迭代次數(shù)。

3 車隊(duì)軌跡規(guī)劃

3.1 協(xié)同區(qū)內(nèi)軌跡規(guī)劃

根據(jù)式（19）確定最優(yōu)狀態(tài)后，被選中的車輛將在各車道內(nèi)協(xié)同組隊(duì)，其過程分兩個(gè)階段。

階段1：車道上的前輛車將組合成一個(gè)車隊(duì)。第1輛車為領(lǐng)航車，位置記為x。其他車輛根據(jù)式（2）所示的跟車策略，調(diào)整與領(lǐng)航車之間的相對位置。

階段2：不同車道的領(lǐng)航車也將調(diào)整其相對位置。為了適應(yīng)合流區(qū)內(nèi)的預(yù)存軌跡，對領(lǐng)航車的軌跡進(jìn)行規(guī)劃時(shí)必須滿足下列條件：

對于?∈S，?＞0，有x()=成立，且≠0。為領(lǐng)航車到達(dá)合流區(qū)的時(shí)刻。為提升交通效率，將協(xié)同過程定義為一個(gè)時(shí)間最優(yōu)的控制問題，構(gòu)建的Bolza問題如下：

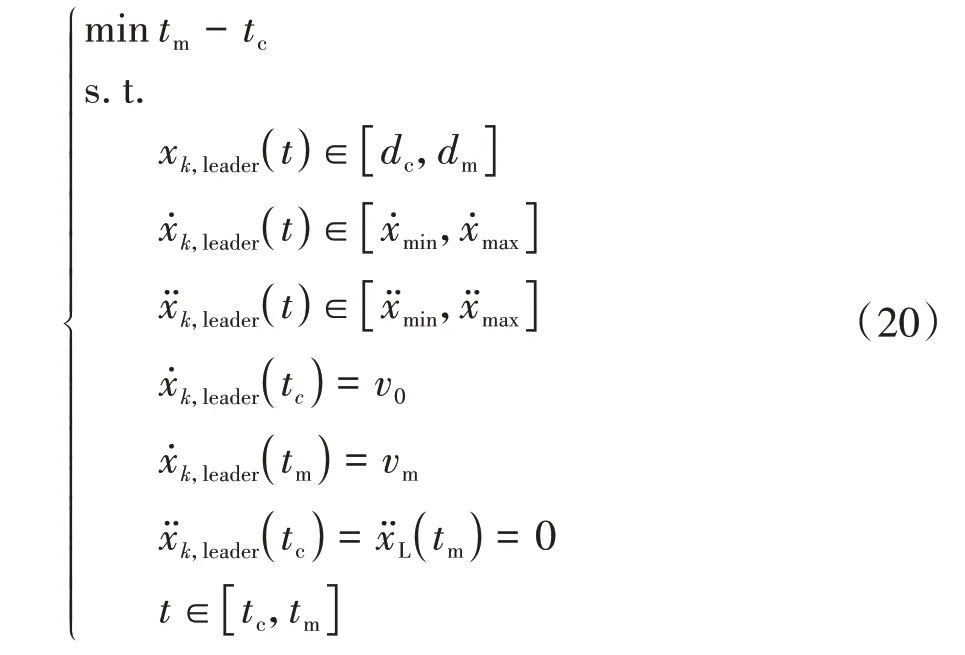
式中為觸發(fā)車輛到達(dá)協(xié)同區(qū)的時(shí)刻。并且，為了交叉口占用時(shí)間不重疊，須施加時(shí)距約束：

式中表示組合中領(lǐng)航車到合流區(qū)的時(shí)刻。此外，當(dāng)領(lǐng)航車執(zhí)行其最優(yōu)軌跡時(shí)，同車道內(nèi)的跟隨車將根據(jù)式（2）進(jìn)行跟車運(yùn)動(dòng)。

3.2 合流區(qū)內(nèi)軌跡規(guī)劃

到達(dá)合流區(qū)的任意組合將受到全局的多車隊(duì)協(xié)同控制，這也是Q學(xué)習(xí)的建模基礎(chǔ)。考慮所有車輛的安全約束，同樣以時(shí)間窗口為最優(yōu)化目標(biāo)，構(gòu)建最優(yōu)控制問題為

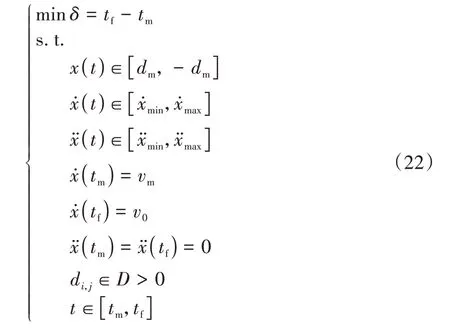
式中：-的負(fù)號表示車輛駛離；為所有車輛離開合流區(qū)的時(shí)刻；安全約束的集合=[，，…，，…，d]；且d表示不同車隊(duì)中車輛之間的距離。具體地，每輛車都將與其他車隊(duì)的所有車輛進(jìn)行約束，即

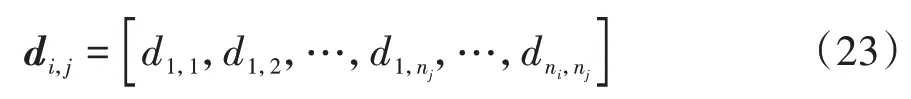
式中n和n分別為車隊(duì)和車隊(duì)的規(guī)模。使用高斯偽譜法對式（20）和式（22）所示的最優(yōu)控制問題進(jìn)行轉(zhuǎn)化，并選擇snopt求解器進(jìn)行計(jì)算。

4 仿真結(jié)果與分析

設(shè)計(jì)了兩種工況，對基于Q模型的組隊(duì)過程進(jìn)行描述，驗(yàn)證所提策略的有效性。在不同車流量工況下，與非組隊(duì)方法及傳統(tǒng)虛擬隊(duì)列方法進(jìn)行對比，驗(yàn)證所提方法的優(yōu)勢。

設(shè)計(jì)式（16）中獎(jiǎng)勵(lì)權(quán)重時(shí)，前后指標(biāo)間的比值分別選為1.8、1.8和1.4，由此確定的權(quán)重系數(shù)以及其他Q模型參數(shù)如表1所示。

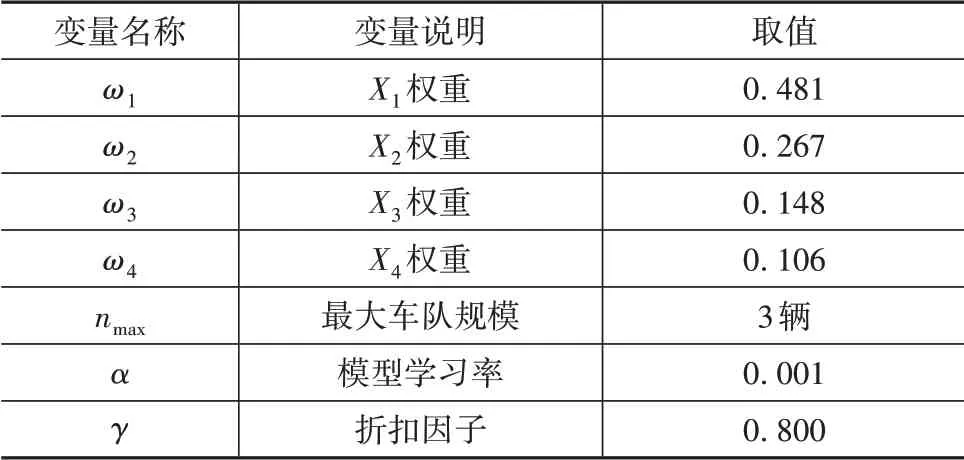
表1 Q模型仿真參數(shù)

4.1 組隊(duì)過程分析

選擇主支路型、流量均衡型交叉口為研究場景，在Matlab/Vissim仿真平臺中定義各車道流量，仿真所需的道路及車輛參數(shù)如表2所示。

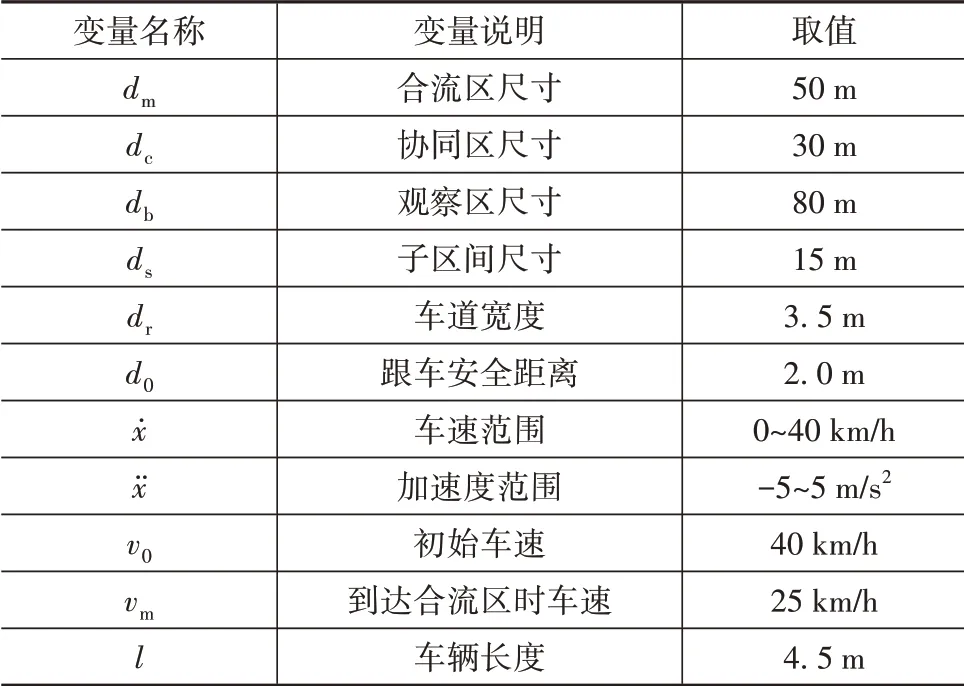
表2 道路及車輛參數(shù)

工況1：主支路型交叉口兩個(gè)方向上的車流量差距顯著，設(shè)計(jì)各車道上的流量為=1600輛/h，=700輛/h，=1800輛/h，=600輛/h。為了描述車輛排隊(duì)的過程，以前兩個(gè)組合的運(yùn)動(dòng)軌跡舉例說明。

如圖5所示，前兩個(gè)組合包含14輛車，仿真前10 s內(nèi)所有車輛均在協(xié)同區(qū)外。在第10.81 s時(shí)，第1輛車到達(dá)協(xié)同區(qū)，根據(jù)車輛位置確定組合1的狀態(tài)向量為=(2，2，2，2)。隨后，組合1中的領(lǐng)航車同時(shí)在19.84 s到達(dá)合流區(qū)，記為。

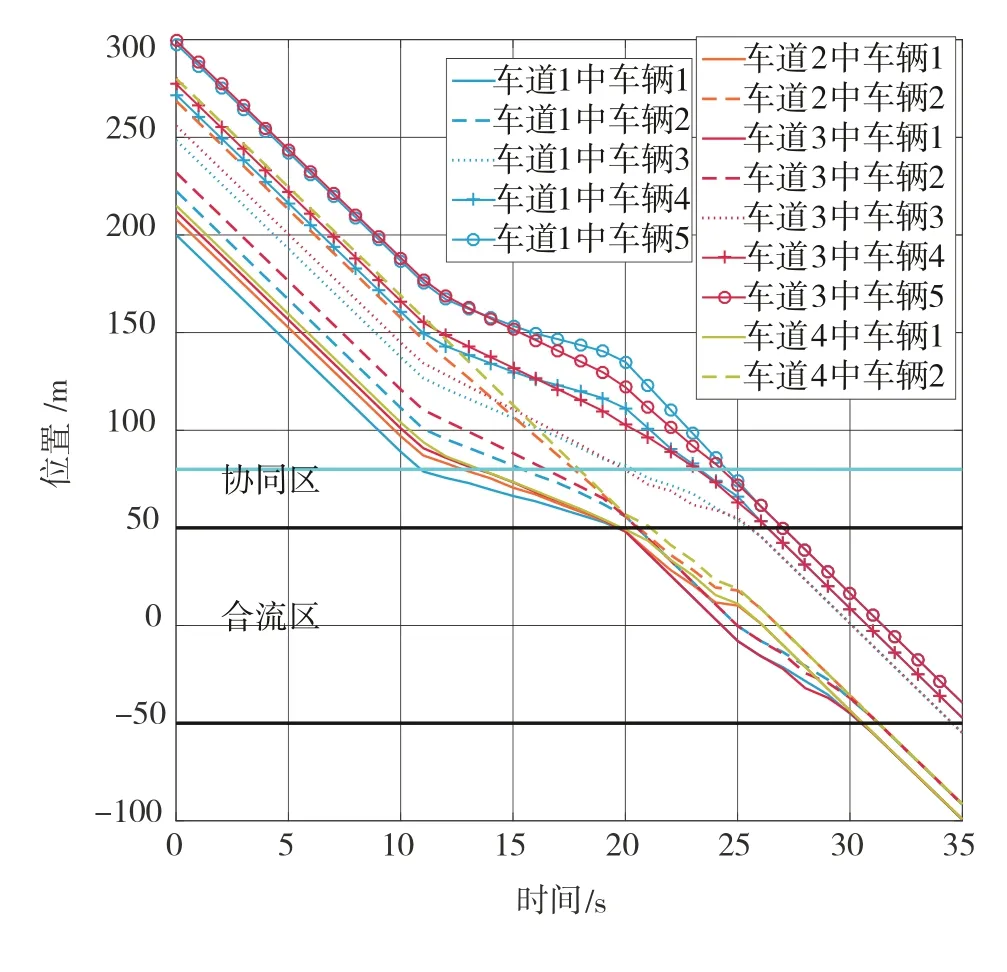
圖5 工況1中的車輛軌跡

另一方面，組合1以外的車輛在第19.75 s到達(dá)協(xié)同區(qū)，并同時(shí)確定組合2的狀態(tài)向量為=(3，0，3，0)。組合2中的車輛在經(jīng)過位置調(diào)整后于第25.64 s到達(dá)合流區(qū)，記為。

為檢驗(yàn)安全性，給出同車道內(nèi)相鄰車輛間的距離，如圖6所示。車流密度的差異導(dǎo)致各車道上的初始車距相差明顯。當(dāng)組合1中的車輛于10.81 s時(shí)開始組隊(duì)，其跟車距離逐漸減小。在組合2形成后，受式（21）的時(shí)間間隔約束，相同車道上不同組合的車輛間距開始明顯增大，如車道1與車道3中的。并且，車隊(duì)進(jìn)入合流區(qū)后將保持車距隊(duì)形，即在運(yùn)動(dòng)的全過程中車距均大于，說明沒有追尾事故發(fā)生。

圖6 工況1中的車間距

工況2：對于流量均衡型交叉口，各支路上的車流密度較接近，設(shè)計(jì)各車道上的流量為=1400輛/h，=1600輛/h，=1500輛/h，=1400輛/h。

此時(shí)，前兩個(gè)組合中共包含24輛車。由于車流密度相近，每個(gè)車道上均有6輛車，其軌跡如圖7所示。圖中，車道2~4上的軌跡線型與車道1線型一致，且顏色屬性與圖5相同。不同于工況1，由于車輛分布均勻且密集，所分配的狀態(tài)向量為==(3，3，3，3)。并 且，兩 個(gè) 組 合 內(nèi) 的 車 分 別 于 第11.08 s和第19.17 s開始組隊(duì)，并于=18.60 s和=26.31 s到達(dá)合流區(qū)。

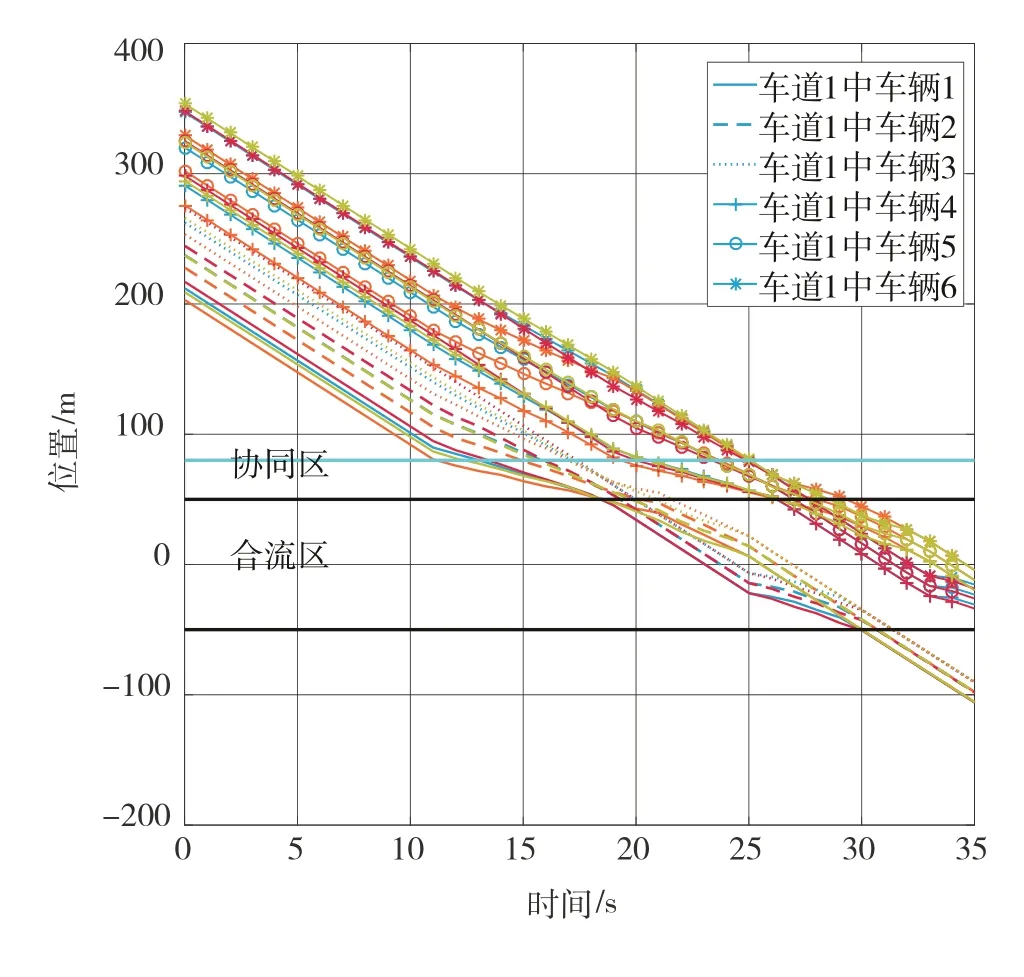
圖7 工況2中的車輛軌跡

工況2中的車距變化曲線如圖8所示，可以觀察到與工況1類似的分組動(dòng)作。并且，所有車輛之間均保持著足夠安全的距離。

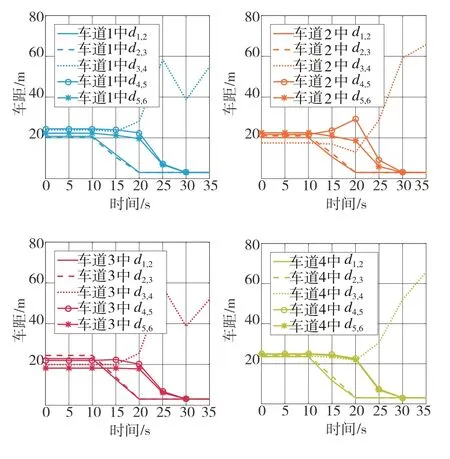
圖8 工況2中的車間距

根據(jù)上述兩個(gè)工況的仿真結(jié)果，可發(fā)現(xiàn)兩個(gè)現(xiàn)象：（1）相比于車輛較為稀疏的情況，大流量工況更利于隊(duì)列的形成，即當(dāng)狀態(tài)向量集包含足夠多的元素時(shí)，所提方法趨向于找到價(jià)值更高的解，驗(yàn)證了Q學(xué)習(xí)模型的有效性；（2）在兩種工況下，都能滿足-＞的條件，說明前后組合之間存在式（21）中定義的空檔期。由此可認(rèn)為上述工況中的車流量均未達(dá)到所提方法的飽和流量。因此，為了驗(yàn)證組隊(duì)方法在大流量工況下的優(yōu)勢，設(shè)計(jì)如下對比試驗(yàn)。

4.2 交通性能對比

為了驗(yàn)證車輛組隊(duì)后的飽和吞吐量，在不同流量工況下進(jìn)行對比仿真。此時(shí)，選擇虛擬隊(duì)列法和非組隊(duì)的離散控制策略作為對比方法，對獎(jiǎng)勵(lì)函數(shù)中的評價(jià)指標(biāo)進(jìn)行比較。仿真時(shí)各車道平均流量為1 200~2 200輛/h，進(jìn)行5次計(jì)算后統(tǒng)計(jì)對比結(jié)果。

如圖9所示，虛擬隊(duì)列法的飽和吞吐量約為3 200輛/h，由于仿真工況均超出其極限值，故計(jì)算結(jié)果標(biāo)準(zhǔn)差較小，在圖中無法顯示。對于非組隊(duì)方法，其通行能力首先隨著到達(dá)車輛的增加而增大。當(dāng)平均流量超過1 800輛/h之后，可知其飽和吞吐量大約為6 250輛/h。因此，1 800輛/h可定義為非組隊(duì)方法的極限工況。當(dāng)車流量小于極限工況時(shí)，吞吐量的計(jì)算值會(huì)因各車道上車流密度的隨機(jī)性產(chǎn)生波動(dòng)，體現(xiàn)為較大的標(biāo)準(zhǔn)差狀態(tài)。對于組隊(duì)方法而言，即使平均流量達(dá)到2 200輛/h時(shí)其吞吐量約可為8 400輛/h，且未達(dá)到飽和狀態(tài)。

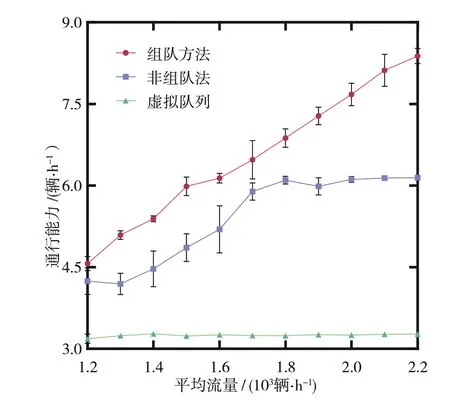
圖9 通行能力對比結(jié)果

因此，可進(jìn)一步對極限吞吐量的理論值進(jìn)行對比。在流量足夠大時(shí)，組隊(duì)方法的最優(yōu)狀態(tài)向量為=(3，3，3，3)。類似地，非組隊(duì)方法的最優(yōu)狀態(tài)向量為=(1，1，1，1)。此外，由于虛擬隊(duì)列方法只允許一輛車進(jìn)入交叉口，則其最優(yōu)狀態(tài)向量為=(1，0，0，0)。3種狀態(tài)下的交叉口占有時(shí)間為4.96、2.25和1.10 s。由式（6）可知，其飽和吞吐量的理論值分別為8 710、6 400和3 273輛/h，與仿真結(jié)果相對應(yīng)。因此，組隊(duì)方式可提升約36.1%的通行能力。

通行能力的差異也表現(xiàn)在行車延誤方面。如圖10所示，虛擬隊(duì)列無法處理大流量工況，隨著車流密度的增大，行車延誤也急劇增大。對于非組隊(duì)方法，在平均流量低于極限工況時(shí)，行車延誤變化不大；在突破極限工況后，延誤數(shù)值急劇增大。對于所提的組隊(duì)方法而言，由于未達(dá)到飽和狀態(tài)，所以交通流的整體運(yùn)動(dòng)沒有受到很大影響。并且，相比于非組隊(duì)的方法，組隊(duì)后的車輛最多可以降低約65%的延誤時(shí)間。

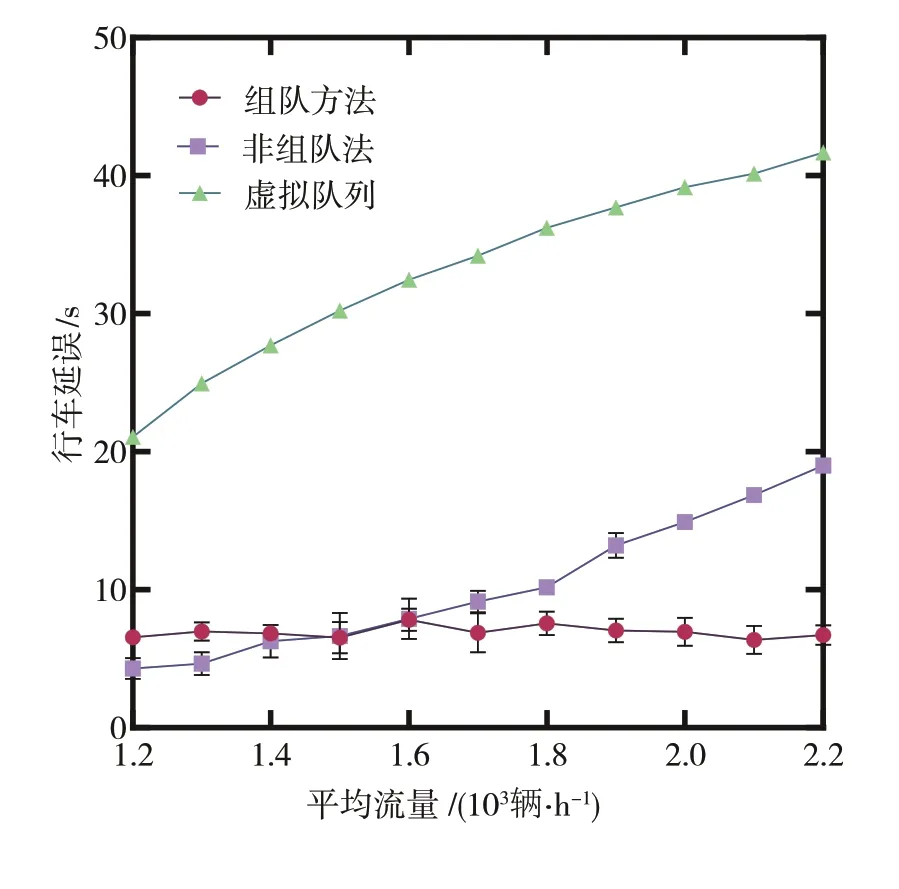
圖10 行車延誤對比結(jié)果

SDTT和油耗在獎(jiǎng)勵(lì)函數(shù)中的權(quán)重遠(yuǎn)小于上述兩個(gè)參數(shù)，因此其對比結(jié)果呈現(xiàn)出不同的特征。如圖11所示，非組隊(duì)方法的SDTT值最小，約為組隊(duì)方法的1/3。就變化趨勢而言，虛擬隊(duì)列法因其行車延誤的增加，SDTT也隨著車流量的增大而增大。對于非組隊(duì)和組隊(duì)方法而言，得益于任務(wù)分解的控制策略，它們的SDTT值在高流量工況中呈下降趨勢。

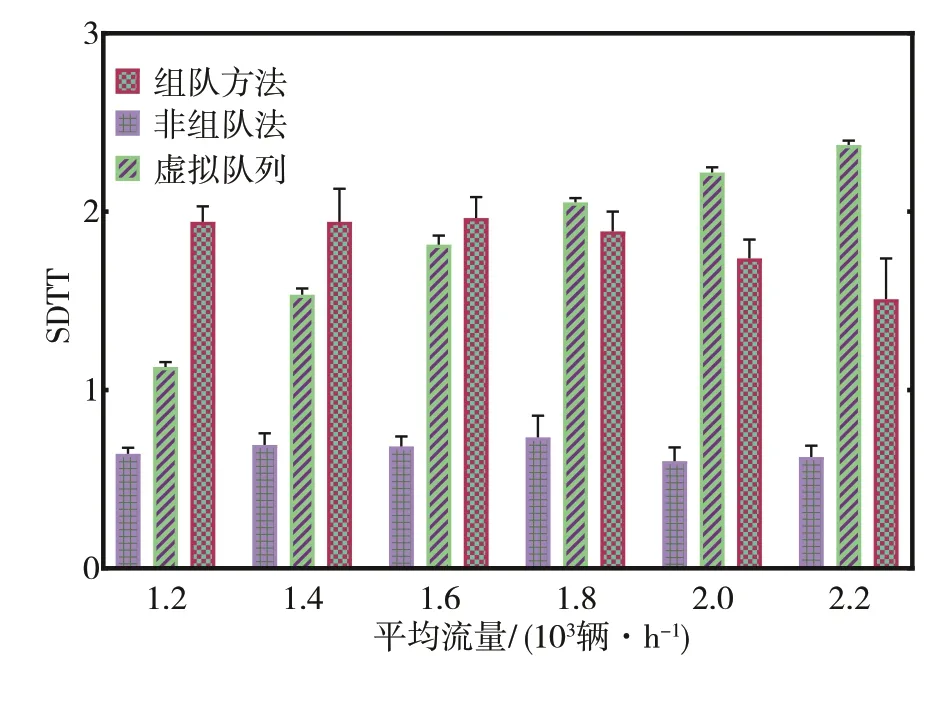
圖11 SDTT對比結(jié)果

類似的特征同樣表現(xiàn)在燃油消耗上，如圖12所示。虛擬隊(duì)列方法的油耗數(shù)值呈穩(wěn)定增長狀態(tài)。另外兩種方法的油耗峰值出現(xiàn)在中等流量工況，此結(jié)論已在作者之前的工作中得到證明。

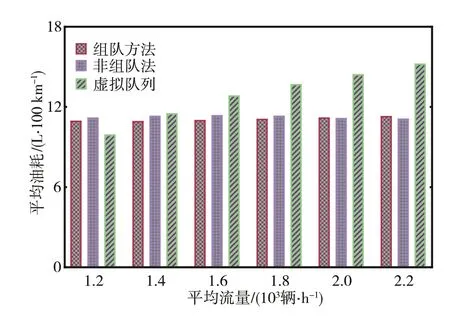
圖12 燃油消耗對比結(jié)果

對比結(jié)果表明，在權(quán)重的影響下，盡管組隊(duì)策略可以提升交叉口吞吐量，但會(huì)略微增加交通流的波動(dòng)和汽車的燃油消耗。

5 結(jié)論

本文中提出一種考慮車隊(duì)的離散控制策略。首先推導(dǎo)出多車隊(duì)協(xié)同軌跡規(guī)劃的篩選約束，并基于此約束設(shè)計(jì)了用于車隊(duì)規(guī)模選型的Q學(xué)習(xí)模型，以通行效率、行車延誤等為復(fù)合指標(biāo)設(shè)計(jì)獎(jiǎng)勵(lì)函數(shù)。

其次，在安全性方面，以跟車模型為基礎(chǔ)，提出了防追尾的安全約束。通過兩種工況的仿真結(jié)果表明了車輛組隊(duì)的有效性，并驗(yàn)證了過程中的安全性。

最后，將所提方法與其他方法進(jìn)行比較，結(jié)果表明組隊(duì)策略可以提升大約36.1%的交叉口通行能力，且無更大的行車延誤。但是，由組隊(duì)引起的自組織過程將使燃油消耗略微增加。因此，在提升交通效率的基礎(chǔ)上，進(jìn)一步降低車隊(duì)油耗也值得深入研究。