面向極限工況的分布式驅動電動汽車動力學集成控制方法*

林 程，梁 晟，宮新樂，于 瀟，汪博文

（1.北京理工大學，電動車輛國家工程研究中心，北京100081；2.北京電動車輛協同創新中心，北京100081；3.清華大學車輛與運載學院，北京100084）

前言

近年來，隨著以我國為代表的新興國家經濟持續快速發展，全球能源需求短期內仍將持續增長，這將會導致煤炭、石油等化石燃料能源短缺問題日益嚴重。因此，我國自“十五”期間以來，一直大力發展新能源汽車，已經將其視為汽車工業彎道超車的重要途徑。在此背景下，能夠進一步提升電動汽車性能的先進控制技術成為了推動新能源汽車持續發展的重要驅動力。在眾多新興技術領域中，分布式驅動作為一種新型純電動汽車構型，有著巨大的發展潛力，吸引了國內外研究機構以及汽車廠商越來越多的關注，已成為近年來的研究熱點之一。該構型由輪轂電機或輪邊電機作為執行器，獨立驅動單個車輪，能夠實現動力系統總體需求轉矩的集中分配與單個車輪轉矩的獨立精確控制，具有動力學控制靈活、主動安全性高的固有特性，更適用于極限工況下的控制需求。因此，本文以分布式驅動電動汽車為研究對象，提出了極限工況動力學集成控制方法，充分挖掘其在極限工況下的控制潛力。

為保證極限工況下的主動安全性，應當首要保證車輛的橫擺穩定性。在現有研究中，橫擺動力學控制方法主要分為兩類：直接橫擺控制（direct yaw control，DYC）與主動轉向控制（active front steering，AFS）。其中，DYC是以驅動電機為執行器，通過分配四輪轉矩產生附加橫擺力矩，從而改善橫擺穩定性的方法。分布式驅動電動汽車各驅動輪采用獨立控制，能夠更容易、更精確地實現轉矩的靈活分配，因此非常適合應用DYC。目前，大多數DYC控制策略采用的分層架構為：上層控制器以橫擺穩定性為控制目標求解得出最優附加橫擺力矩，下層控制器以附加橫擺力矩為跟蹤目標對驅動轉矩進行分配。在上層廣義力控制器中，常用滑模控制（sliding mode control，SMC）、模 型 預 測 控 制（model predictive control，MPC）以及線性二次型調節器等基于模型的控制算法。下層轉矩分配控制器中，應用最為廣泛的則是基于規則的方法與二次規劃（quadratic programming，QP）等優化算法。AFS控制方法則以轉向電機作為執行器，通過計算主動轉向角實現車輛的橫擺穩定性控制。與DYC類似，大多數的AFS控制策略一般也采用SMC、MPC等優化控制算法。此外，一些文獻中提出了綜合AFS與DYC的復合控制方法，結合二者優點，能夠在更苛刻的條件下提升車輛控制效果。

在極限工況中，車輛行駛速度、路面附著等情況復雜多變，僅關注橫擺穩定性的單目標控制方法往往不能滿足控制需求。因此，一些研究將高速轉向、車輪打滑等多個失穩因素綜合考慮，提出了協同優化控制方法。對于協同優化方法來說，在低附著路面轉向時，為了防止車輪打滑導致的車輛失控，應當綜合考慮車輛橫向、縱向動力學，協同控制車輛整體的橫擺穩定性與各個車輪的滑動率；在高速轉向工況中，則需要綜合考慮車輛的橫擺、側傾穩定性。此外，為應對極限工況中控制模型的不確定性與控制系統的外部擾動，一些研究還采用了例如H控制、魯棒MPC控制等方法，提升了車輛動力學控制策略的魯棒性。

然而，現有的極限工況控制方法中，一部分為了降低計算負擔采用線性控制模型，另一部分則為了改善控制精度采用迭代的非線性規劃方法，兩者均沒有很好地平衡精確性與實時性。同時，現有的魯棒控制方法往往將系統擾動假設為最大值，導致控制方法過于保守，甚至出現沒有可行解的情況。此外，多數文獻中的穩定性判據也被忽略或簡化，沒有對極限工況的范圍進行明確定義，具有一定的局限性。

為應對這些問題，本文首先建立了分段仿射（piecewise affine，PWA）輪胎側向力簡化模型，并基于此將非線性橫擺動力學模型轉化為分段線性的混雜系統，在保證建模精度的同時盡量減少控制問題的復雜度。然后，提出了PWA穩定性分析方法，分析了車速、路面附著系數變化條件下的系統分岔點變化機理，將主動轉向角超過系統分岔點后極易失穩的工況定義為極限工況，構造了識別極限工況的車輛穩定性判據。最終，提出了面向極限工況的動力學集成控制方法。為了將多個控制目標解耦，集成控制方法采用了分層控制架構：上層控制器具有多個控制模式，在非極限工況下采用AFS控制模式，在極限工況下則采用AFS+DYC復合控制模式，并利用混雜系統模型預測（hybrid model predictive control，HMPC）方法求解出主動轉向角、車輪縱向力等最優控制輸入，并通過構建混雜系統的Tube魯棒不變集應對控制過程中車速變化導致的預測模型建模失配問題；下層控制器根據上層控制器計算出的最優縱向力分配結果對各車輪滑移率或滑轉率（下文統稱滑動率）進行獨立控制。處理器在環試驗結果表明，本文提出的極限工況動力學集成控制方法能夠在低附著路面雙移線工況、高速雙移線工況等極限工況下，對分布式驅動電動汽車的橫擺穩定性、防滑性能以及側傾穩定性進行協同優化。

1 整車動力學建模

1.1 PWA橫擺動力學模型

為了兼顧極限工況下控制器的精度與實時性，本節對純側偏魔術公式輪胎模型進行分段仿射，將其簡化為關于原點對稱并具有五段線性函數的5段PWA模型。輪胎側向力計算公式如下：

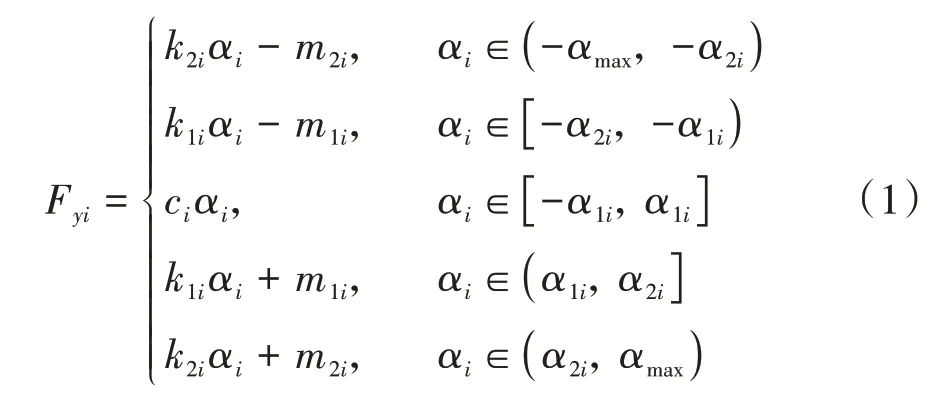
式中：∈｛f，r｝表示2自由度自行車模型中的前、后等效車輪；、為分段仿射輪胎模型的分段點；為側偏角約束的上界；c為第1段線性區域的側偏剛度；、與、分別是第2、3段分段函數的斜率與截距。以路面附著系數為0.85時的輪胎側向力為例，PWA擬合結果如圖1所示。PWA輪胎側向力曲線的擬合誤差如表1所示。

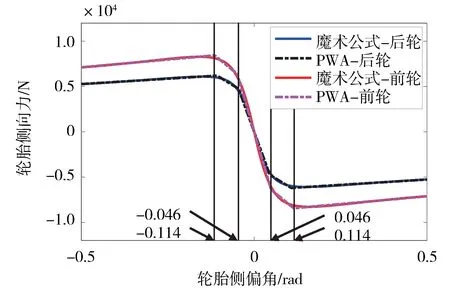
圖1 輪胎側向力擬合結果

由表1可知，5段PWA模型的平均擬合誤差較小，具有較高的擬合精度。

表1 PWA輪胎側向力擬合誤差

將式（1）代入2自由度自行車橫擺動力學模型，并將系統狀態量變為前后車輪側偏角后，可以得到以下PWA橫擺動力學模型：

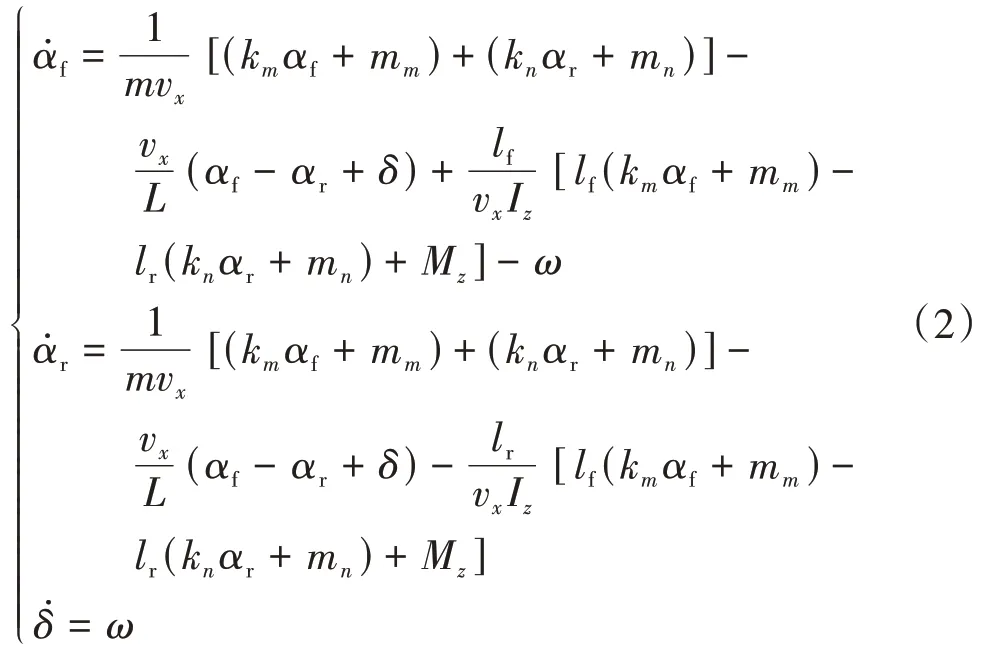
式中：、為前、后輪胎側偏角；為整車質量；v為縱向車速；、為質心到前、后軸的距離；為軸距；為前輪轉向角；M為附加橫擺力矩；k、k分別為前、后輪對應的PWA輪胎力的斜率；m、m分別為相應的截距，其中，下標“”、“”代表前、后輪側偏角處于PWA模型的第、段線性函數上。可以看出，PWA系統共有25個線性控制區域，當前控制區域由下標“”、“”確定。

本文提出的上層控制器是通過跟蹤期望的橫擺角速度實現橫擺穩定性控制的，因此，為了消除橫擺角速度的跟蹤誤差累積所導致的車輛方向偏轉，本節建立的模型中加入如下的離散系統誤差累積項：

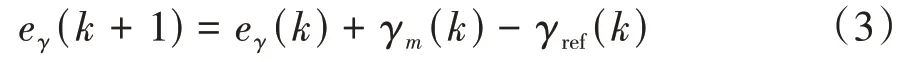
式中：γ為控制器計算出的實際值；為期望值。根據線性側偏假設下的駕駛員輸入轉角計算得到，其表達式如下：

式中：為駕駛員輸入的轉向角；、為參數。

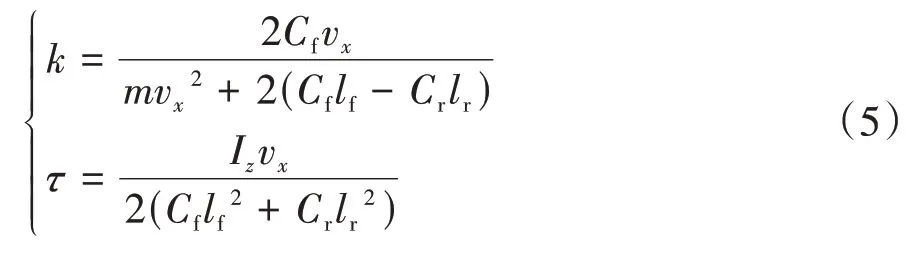
式中：I為繞軸的轉動慣量；、為前后輪的線性區側偏剛度。

為了簡化控制邏輯，縮短整個控制策略的控制周期，本文將傳統分層控制架構的廣義力計算層與轉矩分配層合并，直接以四輪縱向輪胎力作為控制輸入。附加橫擺力矩M與四輪縱向輪胎力的關系為

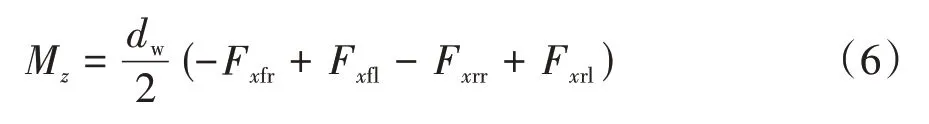
式中為車輛的輪距。

令=［，，，e］為狀態向量，橫擺角速度=為輸出量，=［，F，F，F，F］為輸入量，并利用向前歐拉法將模型離散化，式（2）的離散狀態空間表達式可以表示為

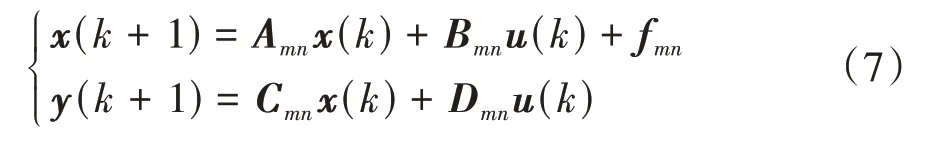
與式（2）類似，式中的下標“”表示此時前、后側偏角處于PWA模型的第、段線性函數上。式（7）中的系數矩陣與常數項為

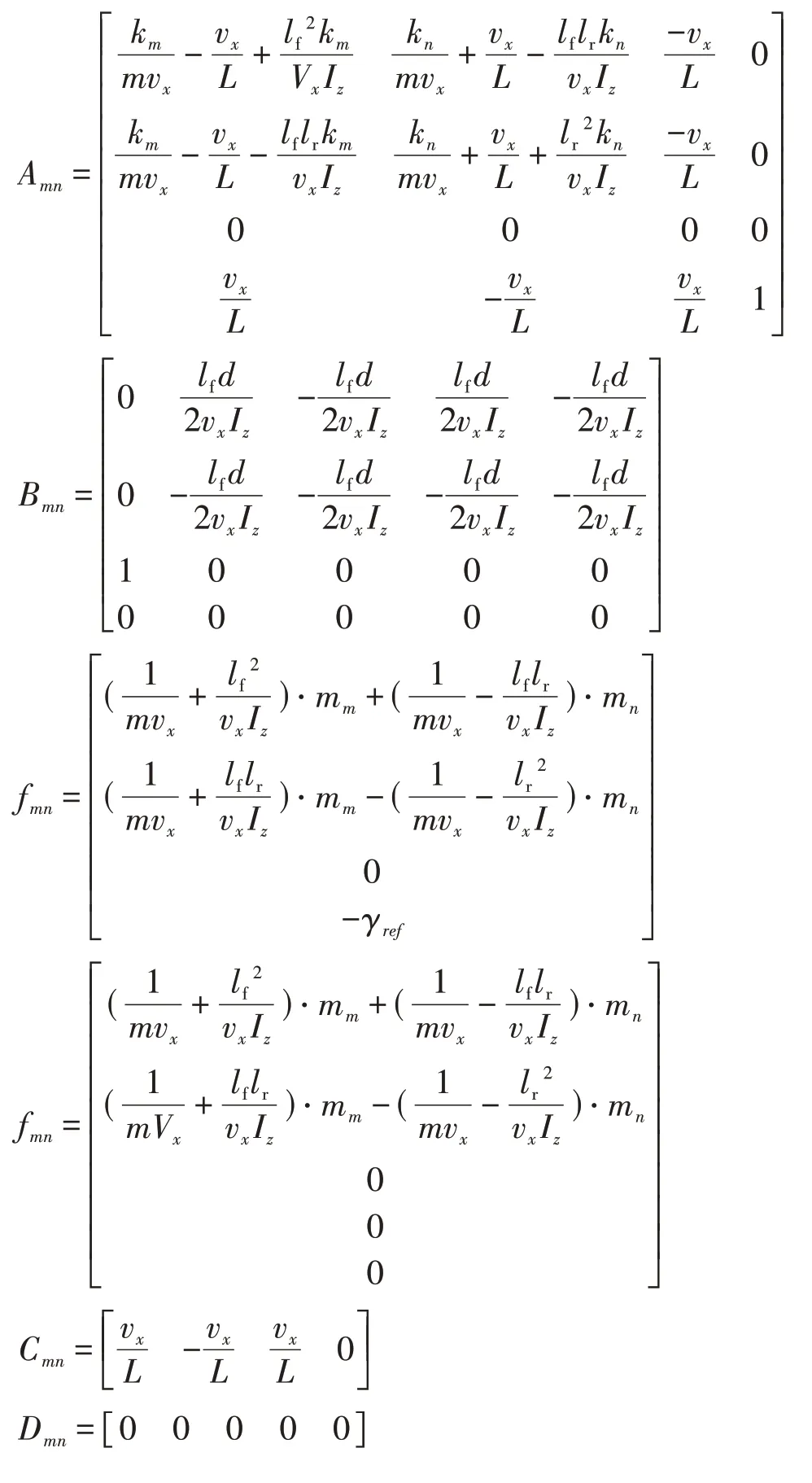
1.2 驅動輪動力學模型

單個驅動輪的受力分析如圖2所示，其中，下標，∈｛f，r｝。其力矩平衡微分方程為

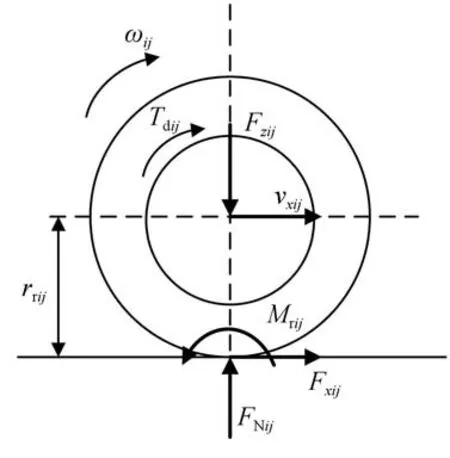
圖2 驅動輪受力分析圖

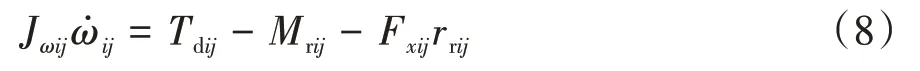
式中：ω為車輪角速度；J為車輪轉動慣量；為輪上的輸出轉矩，以驅動方向為正方向；為滾動摩阻；F為輪胎縱向力；為滾動半徑。

在本文提出的動力學集成控制策略中，上層控制器使用的時純側偏假設下的輪胎側向力模型。為了保證上層控制器的建模精確性，下層控制器在跟蹤各車輪的目標滑動率時，應當盡量將其限制在一個較小的范圍內。因此，本節將滑動率與車輪縱向力視為線性關系，可以由下式表示：

式中為輪胎縱向力的等效斜率。

綜上，單個車輪的滑動率跟蹤控制器的動力學模型可以表示為

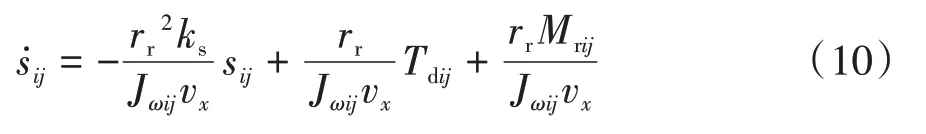
令=s為狀態量，=為輸入量，=為輸出量，并對式（10）進行離散化，寫為以下離散的狀態空間表達式：

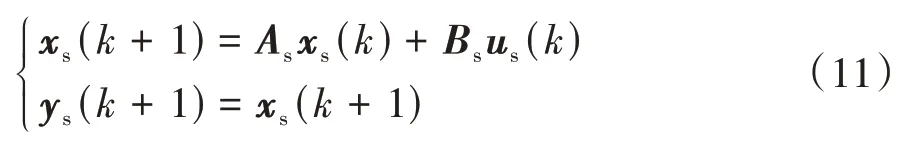
2 車輛失穩機理分析與穩定性判據

在復合極限工況中，存在高車速、低附著、大轉角轉向等情況，此時車輛穩定性區域會發生明顯的變化，甚至有可能會導致系統的分岔現象（即相平面中的不動點的數量或類型發生突變）。當系統發生分岔時，穩定區域將會發生突變，此時，車輛極易失穩，橫擺動力學控制的難度將顯著增加。因此，本文將能夠導致車輛橫擺動力學系統發生分岔的工況定義為極限工況。

2.1 車輛失穩機理分析

由于非線性系統的不動點難以解析求出，本文基于PWA簡化模型在速度、路面附著系數等多參數變化條件下計算每個線性控制區域不動點的位置與類別，并分析系統的分岔行為。

穩態轉向角下的系統不動點位置可以通過求解以下方程得到對于系統的每一個線性控制區域，式（12）的解為

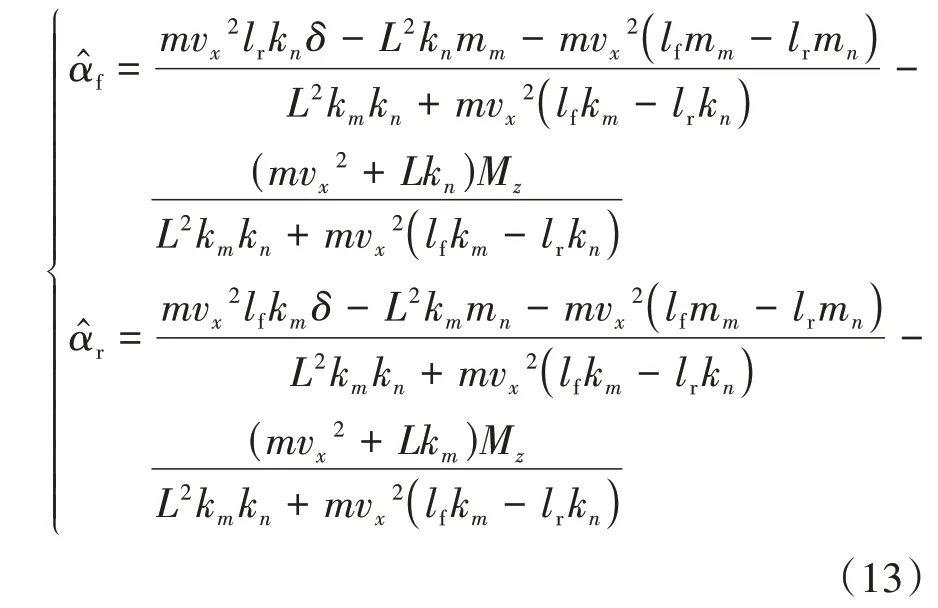
在本文提出的集成控制策略中，當車輛處于非極限工況下控制模式為AFS模式，此時控制輸入僅有前輪轉向角。因此，本文將僅與前輪轉角相關的分岔點作為極限工況的判據。

不動點的類別可以通過特征值來判定。首先，求解以下系統狀態矩陣的特征方程：

式中A為連續系統的狀態矩陣。求解后，將兩個特征值表示為，不動點的類型可以由算法1所示的偽代碼得到：

算法1：不動點類型判別1.輸入：特征值λ1、λ2 2.if λ1λ2＞0 then 3.不動點為鞍點4.elseif Re（λ1）＜0 and Re（λ2）＜0 then 5.不動點不穩定6.elseif（λ1+λ2）2-4λ1λ2＞0 then 7.不動點為穩定焦點8.else 9.不動點為穩定結點10.輸出：不動點類型

以車速v=15 m/s，路面附著系數=1時的系統為例，在∈［-0.5 rad，0.5rad］范圍內，利用算法1求出的系統不動點軌跡如圖3所示。圖3（a）中，紫色實線為穩定結點的軌跡，藍色實線為穩定焦點的軌跡，綠色實線為鞍點的軌跡，紅色虛線為PWA模型控制區域的分界線。可以看出，當前輪轉角變化時，會導致系統在某一時刻發生分岔現象，此時前輪轉角值稱為系統分岔點。由于圖3（a）所示的軌跡是基于PWA簡化模型得出的，與原非線性系統存在偏差。為了驗證圖3（a）所示結果的準確性，圖3（b）將原非線性系統的相平面與算法1求出的不動點軌跡進行了對比，此時前輪轉向角為0.2 rad，藍色、綠色圓圈分別為相平面中穩定焦點與鞍點。可以看出，基于PWA簡化模型得出不動點軌跡雖然存在一定的誤差，但是具有較好的計算精度。因此，本文將PWA系統的分岔點作為極限工況與非極限工況的臨界點。將圖3中的PWA模型控制區域如圖4所示進行編號后可知，系統分岔現象出現在不動點由18號區域移動至17號區域以及9號區域移動至10號區域時，此時對應的分岔點為=±0.1130 rad。

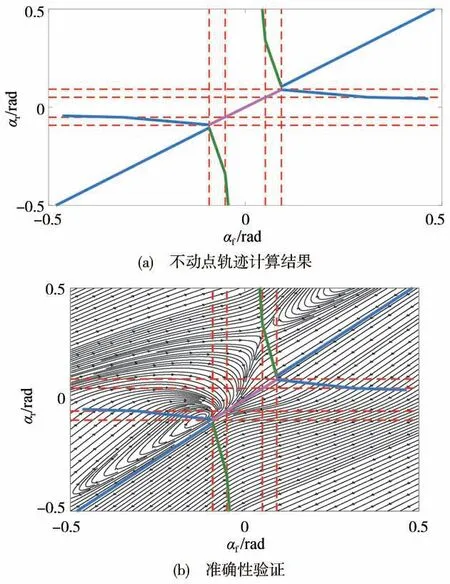
圖3 系統不動點軌跡

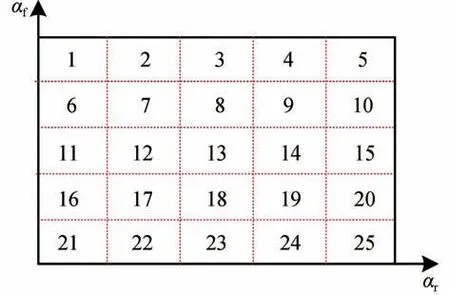
圖4 控制區域編號示意圖

為了進一步分析車速、路面附著系數對系統分岔點的影響，本文在15~30 m/s的車速范圍與1~0.2的路面附著系數取值范圍內等間隔選取了多組參數，并應用算法1對各組參數對應的系統分岔點進行了計算。其中，車速取值間隔3 m/s，路面附著系數取值間隔為0.1。多參數變化時分岔點的計算結果如圖5所示。

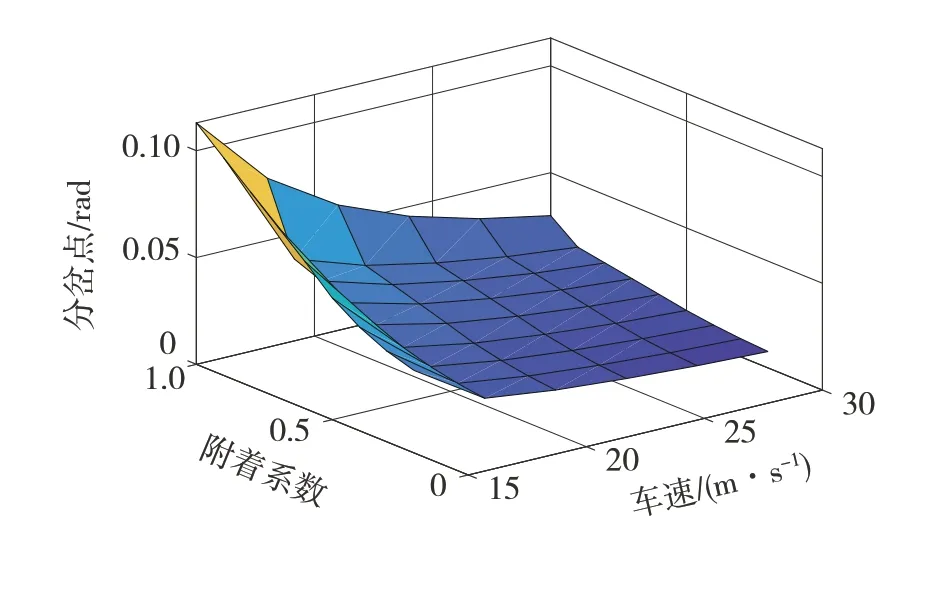
圖5 多參數變化時的系統分岔點

如圖5所示，當附著系數降低或車速上升時，系統分岔點會明顯減小。由此可知，車輛在高速、低附著工況下行駛時，即使轉向角較小也有可能導致分岔現象的發生，更容易進入極限工況。在本文后續提出的車輛穩定性判據中，將利用圖5的結論以車輛當前的車速、路面附著系數對應的分岔點作為控制模式切換的閾值。

2.2 車輛穩定性判據

將分岔點表示為車速與路面附著系數的函數，極限工況的判定方法可以由下式表示：

車輛穩定性判據與相應的控制模式可以歸結為：當車輛轉向角不符合式（15）的條件時，車輛沒有處于極限工況，控制策略采用AFS模式，狀態量的物理約束為=0時的穩定區域；當車輛轉向角符合式（15）時，判定車輛處于極限工況，控制策略切換至AFS+DYC復合控制模式，狀態量的物理約束為=±時的穩定區域。此外，為了防止車輛控制模式頻繁切換，只有當前輪轉角重新回到安全范圍內并持續1 s時，才會判定車輛已經退出極限工況。

3 極限工況動力學集成控制策略

本文提出的動力學集成控制策略具有分層控制結構，整體架構如圖6所示。上層控制策略首先基于第2部分提出的PWA橫擺動力學模型轉化為混合邏輯動態（mixed logical dynamical，MLD）預測模型；然后采用混雜模型預測控制（hybrid model predictive control，HMPC）算法進行優化問題的求解；同時，在控制過程中將車速變化視為有界擾動，構造了偏差系統的Tube控制不變集，提升了上層控制策略的魯棒性。下層控制器以車輛驅動防滑性能為控制目標，對各驅動輪的滑動率進行獨立控制。

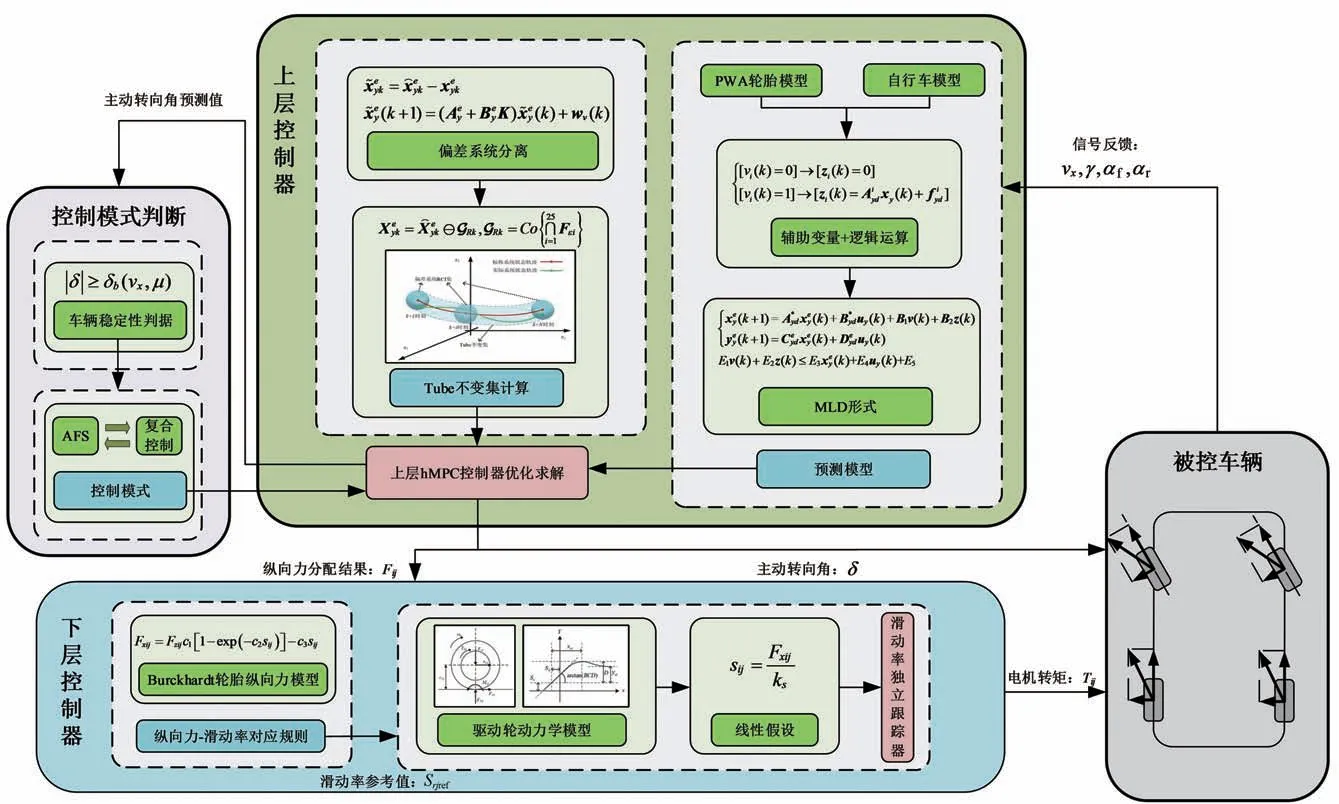
圖6 動力學集成控制架構

3.1 上層橫擺穩定性控制

大多數基于PWA模型的控制方法會通過一組切換條件將各區域的動力學模型聯合為一個切換系統，當滿足某個切換條件時會將系統模型切換至某一區域。然而，對于MPC控制系統來說，當實際狀態量接近切換點時，由于單個有限時域求解過程中無法切換預測模型，會使得狀態量保持在當前的區域內，無法根據實際的狀態量進行切換，導致控制效果受到影響，甚至導致有限時域優化問題無可行解。因此，本文通過引入邏輯輔助變量與連續輔助變量，將PWA模型的切換條件表示為一組混合整數線性不等式約束，從而建立MLD預測模型。

首先，引入輔助邏輯變量∈｛0，1｝，其中=25為整個系統的區域數量，由、的分段數量相乘得到。引入后，式（7）可以改寫為

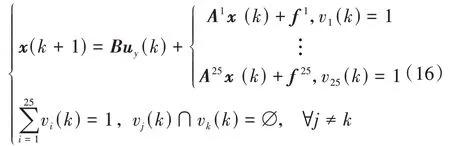
式（16）的內涵為當系統狀態進入第個區域時等價于v（）=1。因此，式（16）可以改寫為

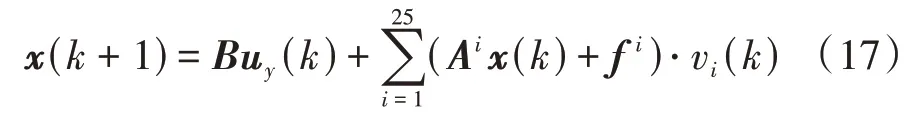
假設系統狀態向量的容許集為多面體，式（17）第2項的上界與下界可以定義為

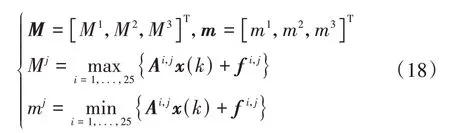
式中上標∈｛1，2，3｝代表系統中第個狀態方程式。為了方便理解，式（18）可以解釋為：上界與下界為單獨求出各個狀態方程式在約束中的最大、最小值后重新組合的向量。其中，與可以由數值的方法求出。

引入以下新的連續輔助變量：

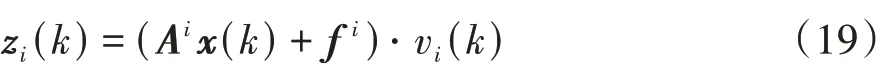
易知，與滿足以下布爾關系式：

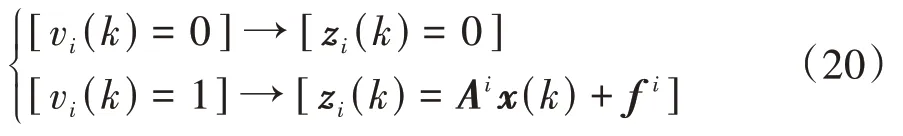
式中“→”為包含關系的布爾運算符。

綜合式（17）、式（18）與式（20），系統狀態方程可以寫為如下的形式：

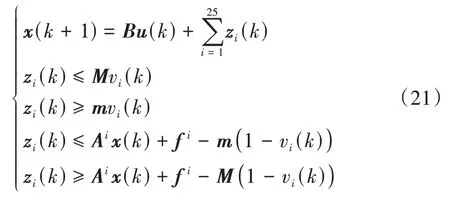
綜上，預測模型可以寫為如下MLD形式：

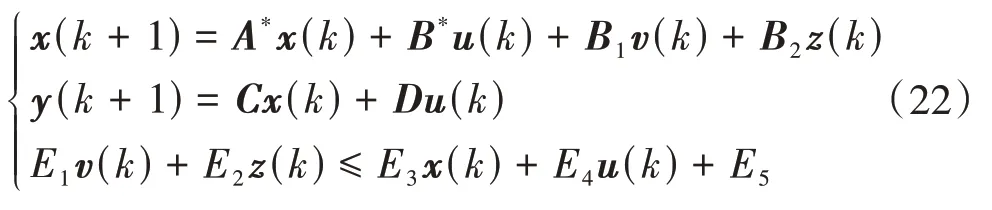
本文使用基于MATLAB的HYSDEL工具箱計算MLD模型中的各矩陣。

值得注意的是，當穩定性判據沒有判定車輛處于極限工況時，控制輸入中的四輪縱向力固定為左右兩側轉矩平均分配模式，不進行優化求解。穩定性判據使用的前輪轉角為上一次有限時域優化計算出的輸入序列的第二個值。

雖然MPC的滾動優化機制可以在一定程度上提高控制器魯棒性，但是當車速變化幅度稍大時，還是會對控制效果造成負面影響。因此，為了提高控制策略的魯棒性，本文將車速的變化視為系統的有界外部擾動，將系統的確定部分與擾動部分分離，將式（22）無擾動的系統稱為標稱系統，然后根據擾動的范圍利用狀態反饋控制在標稱系統狀態軌跡的鄰域構造一個實際系統狀態量的“管道”，即Tube不變集，并將去除Tube不變集后的系統物理約束作為標稱狀態容許集，最后求出使標稱狀態量維持在該在容許集內的最優輸入，使狀態軌跡保持在Tube不變集內，保持系統穩定。圖7為Tube不變集的示意圖，如圖所示，盡管車速變化導致的外部有界擾動使實際系統狀態軌跡偏離了標稱狀態軌跡，但實際系統的狀態軌跡仍然可以保持在標稱系統狀態軌跡周圍的Tube不變集中。

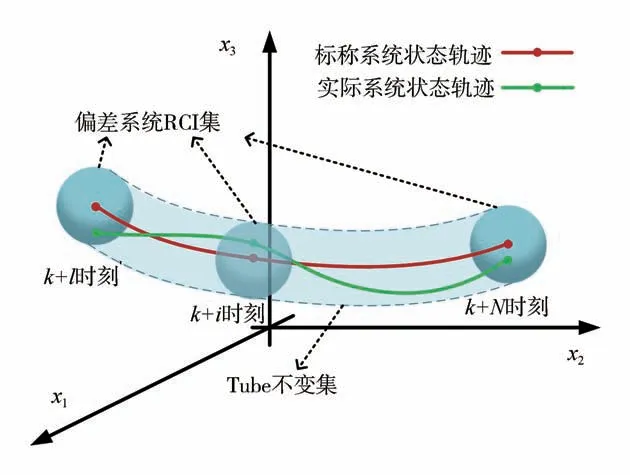
圖7 Tube不變集示意圖

首先，將車速變化作為有界的外部擾動，實際系統的離散系統狀態方程可以寫為

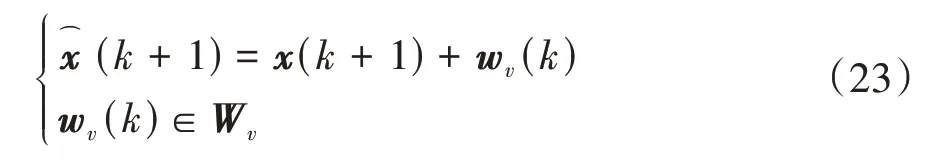
式中w為車速變化帶來的外部擾動，其范圍是干擾集W。值得注意的是，由于車速擾動是有界的，W為一個包含原點的緊集。

為了描述實際系統與標稱系統之間的偏差，定義偏差系統的狀態量為

同時，經過狀態反饋增益調整后的實際系統輸入量可以寫為

式中為狀態反饋增益，滿足Hurwitz條件。

根據式（23）-式（25），偏差系統狀態方程可寫為

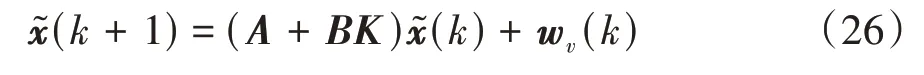
為了方便后續描述，將矩陣+表示為。

下面將對偏差系統在有界車速擾動下的魯棒控制不變集（robust control invariant，RCI）進行計算，并將其作為控制系統的Tube不變集。

當一個偏差系統狀態量的集合滿足以下條件時，稱其為偏差系統的一個RCI集：

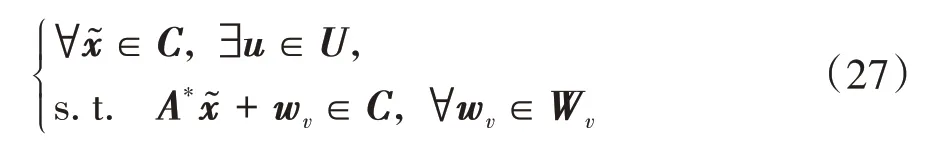
為了兼顧閉環控制系統的可行性與魯棒性，應當盡可能增大標稱系統狀態量容許集，并使實際狀態軌跡盡量貼近標稱狀態軌跡，為達到這一目的，Tube不變集應當盡可能小。因此，本文將計算偏差系統的最小RCI集作為偏差系統Tube不變集。大多數系統的最小RCI集難以解析求出，因此本文采用近似集來逼近最小RCI集。

當一個集合C滿足以下條件時，稱其為最小RCI集C的一個近似集：

式中：為一個很小的正數；⊕表示集合的Minkowski和。

然后，將包含原點的有界干擾集W表示為如下一般形式：

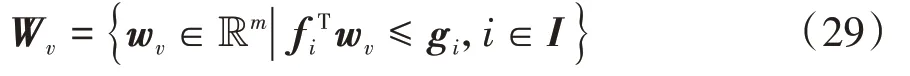
式中：f∈R；g∈R；為一個由車速變化范圍決定的有限集。

則C的計算方法可以表示為算法2：

算法2：Cε計算方法1.輸入：Wv，A*，ε=10-6 2.初始化：s：=0，M：=1，α：=1 3.while（α＞ε/(ε+M(s))）do 4.begin while 5.s：=s+1 6.α=α（s）7.M=M（s）8.end while 9.Cε=(1-α)-1(⊕∞i=0(A*)iWv)10.輸出：Cε

其中，（）計算方法為

式中：e為維實數空間第個單位基向量；h為擾動上確界函數。

（）計算方法為

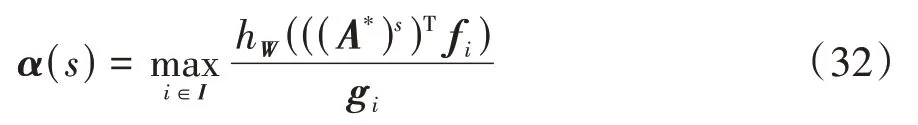
通過算法2，可以計算每個控制區域對應的線性系統的最小RCI集近似集，兼顧了所有控制區域，并滿足凸優化問題的求解條件，混雜系統的Tube不變集由下式計算得到：

式中：C(∈{1，...，25})為各區域最小RCI集的近似集；{?}為凸包運算。本文借助MATLAB軟件內置的MPT工具箱完成集合運算。

式（33）中構造的Tube不變集包含了所有控制區域下偏差系統的最小RCI集，在進行基于標稱系統的hMPC優化控制時，無論狀態量處于哪個控制區域中，都可以保證實際系統的狀態軌跡在有界車速擾動存在的情況下保持于Tube不變集內。由于各區域內偏差系統的最小RCI集都是原點附近的鄰域，即便凸包運算在一定程度上擴大了Tube不變集的范圍，式（33）中的計算方法仍然保證控制系統不會過于保守。

求出Tube不變集后，預測時域內標稱狀態量與標稱輸入量的容許集、可以寫為

式中：、為實際系統狀態量與輸入量的物理約束；$表示集合的Pontryagin差。

綜上，上層控制器有限時域優化問題表示為

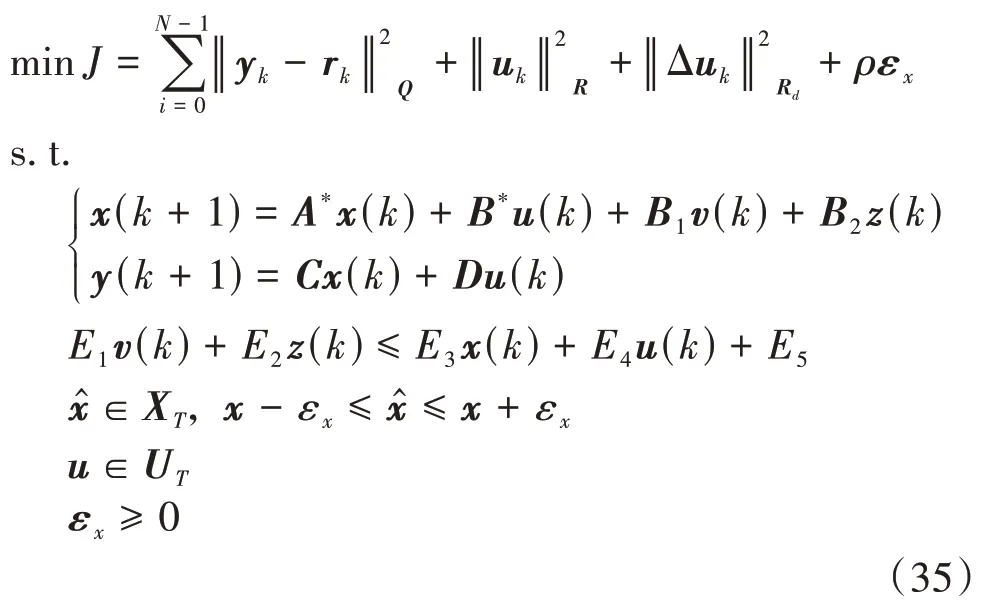
式中：為預測時域；y、r、u分別是輸出量、參考量、輸入量在有限預測時域內的序列；、、R分別為輸出量誤差權重矩陣、控制輸入權重矩陣、控制輸入變化率權重矩陣；為松弛權重系數，一般被設置為一個遠大于其余權重矩陣內元素的正數；ε為狀態約束的松弛變量。代價函數前3項分別懲罰輸出量與期望值的誤差、控制輸入的幅度、控制輸入的變化率；第4項是狀態約束松弛項，其作用是保證hMPC的持續可行性，當hMPC控制器在無松弛的容許集式（34）內存在可行解時，由于遠大于其余3項的權重矩陣，當狀態松弛變量ε增加時，會被迅速地被懲罰至0附近，此時約束不會被松弛；而當容許集式（34）內無可行解時，狀態松弛變量ε會適當增加，使狀態量的容許集擴大，保證hMPC的有限時域優化問題在新的狀態容許集中有可行解。

由于預測模型與不等式約束中均帶有只能取整數的邏輯變量，在求解hMPC的有限時域優化問題時需要用到混合整數規劃求解器，由于該類問題求解的計算量遠大于一般的連續變量規劃問題，為了保證算法的實時性，本文利用混合整數線性規劃（mixed integer quadratic programming，MILP）方法求解上層控制器的有限時域優化問題。

3.2 下層滑動率跟蹤控制

上層控制器的輪胎側向力是基于純側偏工況輪胎模型計算的，而本章定義的極限工況包含了低附著路面情況，當車輪在低附著路面打滑嚴重時，輪胎將會進入縱滑-側偏聯合工況，上層控制器的控制效果將大打折扣。因此，本節提出的下層滑動率跟蹤控制器的控制目標是獨立跟蹤中間層計算出的各車輪滑動率目標值，并且將各車輪滑動率的數值限制在較小的范圍，以保證動力學集成控制策略在低附著路面的控制效果。

首先，本文使用Burckhardt輪胎模型來建立不同路面附著條件下的縱向力-滑動率對應規則。Burckhardt輪胎模型中，輪胎縱向力可以表示為

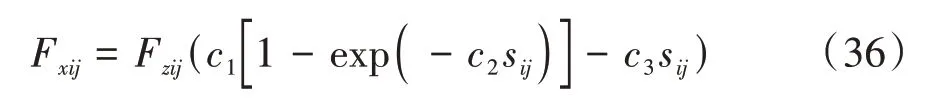
式中c、c、c為擬合系數，會隨著附著條件而變化。不同附著條件下的擬合系數如表2所示。

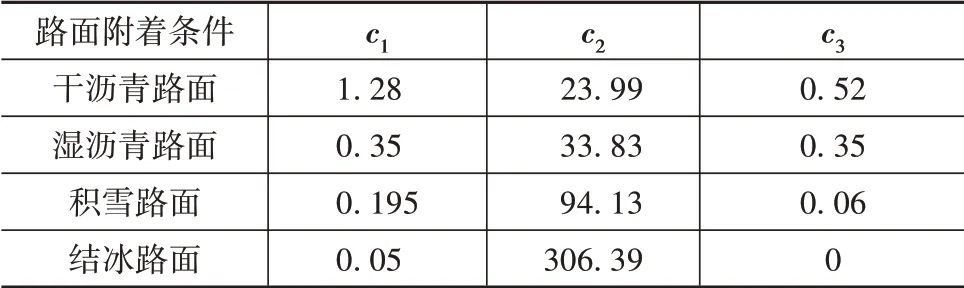
表2 不同附著條件下的擬合系數

由于下層控制器將滑動率限制在線性區域內，因此，縱向力-滑動率對應規則最終可以由式（9）中的線性方程表示，式中的輪胎縱向力的等效斜率由式（36）與表2獲得。上層控制器計算得到的4個車輪的最優縱向力可以根據式（9）轉化為目標滑動率。

然后，以式（11）作為預測模型，下層控制器采用線性MPC算法進行滑動率跟蹤控制。其有限時域優化問題可以寫為

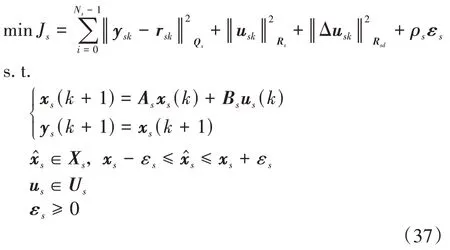
式中：N為預測時域；y、r、u分別是輸出量、參考量、輸入量在有限預測時域內的序列；Q、R、R分別為輸出量誤差權重矩陣、控制輸入權重矩陣、控制輸入變化率權重矩陣；ρ為松弛權重系數，ε為狀態約束的松弛變量；U為控輸入的容許集；X為滑動率的容許集，由當前路面附著條件下輪胎縱向力曲線決定。在本文仿真中，高附著路面為s∈［-5%，5%］，低附著路面為s∈［-3%，3%］。

4 處理器在環試驗驗證

本文提出的控制算法包括了極限工況下的動力學集成控制方法，實車試驗危險性較大，并且試驗場地及條件苛刻。因此，利用本課題組的dSPACE實時仿真機與MicroAutoBox II等設備搭建了處理器在環（processor-in-the-loop，PIL）試驗平臺，以線性MPC橫擺穩定控制器（路面附著系數、輪胎側偏剛度均為常數）作為對比算法，在對開路面雙移線（double lane change，DLC）與高速DLC工況下進行了驗證。

4.1 PIL臺架搭建

本文使用的PIL試驗平臺如圖8所示。PIL平臺中，被控對象為四輪分布式驅動電動乘用車，其動力學模型與工況環境模型基于dSPACE Automotive Simulation Models（ASM）搭建，在仿真過程中運行于Midsize Simulator實時仿真機中，其基本參數如表3所示。為了在算法調試初期分別驗證穩定性判據與動力學集成控制，兩部分控制軟件分別運行于獨立的硬件中。其中，由于本文提出的動力學集成控制策略有一定的在線計算負擔，其首先被搭建在基于Matlab/Simulink的控制模型中，再利用dSPACE公司開發的Targetlink工具生成相應的C語言代碼，最后運行于算力較高的Micro AutoBox II中；由于穩定性判據控制軟件在線計算量小，其被單獨刷寫于一個嵌入式整車控制器（vehicle control unit，VCU）中，根據環境信息來決策控制模式。此外，駕駛員輸入的驅動/制動踏板、轉向盤等控制指令由一臺PC電腦通過ControlDesk軟件進行模擬。仿真平臺中，所有設備間的通信方式均為CAN通信，由Kvaser CAN卡實現USB信號與CAN總線信號的轉換；VCU、Micro AutoBox II等設備由一個可調低壓電源供電。為提高控制系統實時性，本文利用高性能求解器FORCES pro求解有限時域優化問題。

圖8 基于dSPACE的HIL試驗平臺

表3 車輛基本參數

4.2 對開路面雙移線工況驗證

對開路面工況如圖9所示，道路中的紅色圓圈代表DLC工況的錐形桶，上下兩車道路面附著系數分別為0.2與0.85，行駛車速為55 km/h。

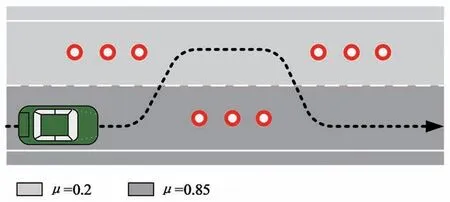
圖9 對開路面雙移線工況示意圖

圖10為本文提出的集成控制策略與線性MPC控制器的效果對比。本文提出的集成控制方法在高附著路段中平均路徑跟蹤誤差為線性MPC的76.39%，在低附著路段中僅為線性MPC的3.19%，控制精度提升顯著。由圖10（a）可以看出，本文提出的動力學集成控制策略可以在圖10（b）所示的車速變化擾動下，在對開路面上很好地實現目標軌跡的跟蹤，橫向位置在DLC結束時也能夠迅速回到初始位置。另一方面，動力學集成控制策略存在輕微的控制延時，這是因為控制策略采用了分層架構，在控制時下層控制器計算出的電機轉矩實際上是上一個控制周期對應的最優電機轉矩。在本文提出的控制策略中，控制周期為50 ms，因此，控制器的延時也為50 ms。雖然線性MPC控制器也能在高附著路面上實現目標軌跡的跟蹤，但當車輛進入低附著路面時，跟蹤誤差明顯大于動力學集成策略，在DLC結束后橫向位置經過一段時間的震蕩才回歸初始位置。

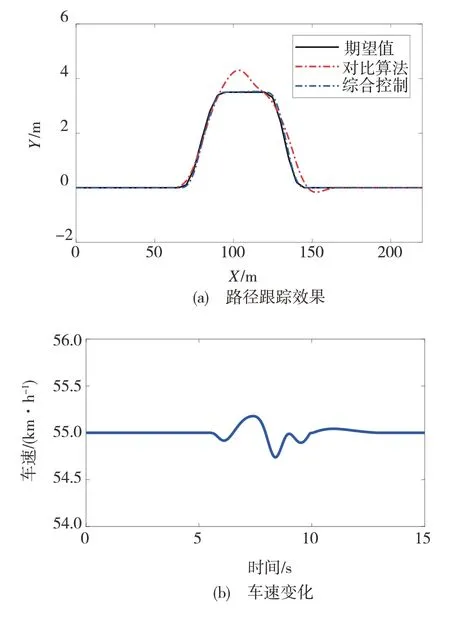
圖10 控制效果對比

圖11展示了控制過程中動力學集成控制策略與對比算法的前、后輪胎側偏角的控制效果。在車輛從高附著路面進入低附著路面時，集成控制策略產生的前、后輪側偏角出現了波動，這是由于此時控制模式發生了改變，這一結論在圖12中展示的控制輸入仿真結果中也有體現。而線性MPC控制器產生的前輪側偏角在進入低附著路面后，前輪側偏角明顯大于集成控制策略，已進入非線性側偏區域，使得輪胎側偏剛度發生了變化；然而，由于其預測模型是基于線性化的模型建立的，在此情況下將會導致建模失配問題，使控制效果大打折扣。

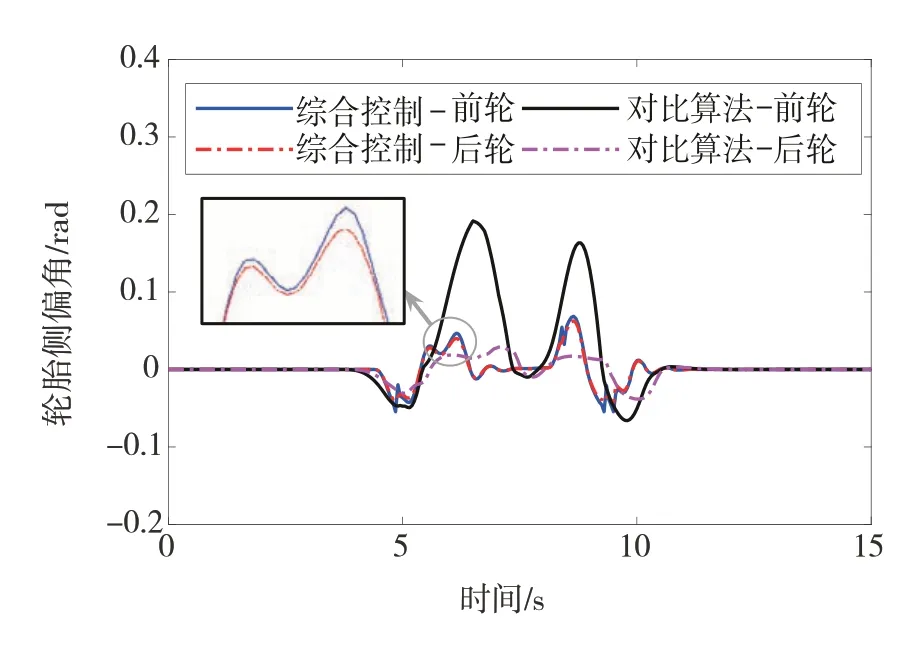
圖11 輪胎側偏角結果對比

圖12 動力學集成控制最優輸入結果

圖12展示了對開路面DLC工況中動力學集成控制策略計算出的最優輸入。如圖所示，在控制過程中，當車輛在高附著路面或轉向角較小時控制模式為AFS模式，不產生橫擺力矩；控制模式僅在低附著路段中轉向時切換為AFS+DYC復合控制模式，此時控制模式的切換也導致了圖11中變量的波動。

圖13展示了對開路面DLC工況中動力學滑動率的仿真結果。如圖所示，在控制過程中，滑動率被限制在較小的范圍內，符合前文規定的范圍（高附著路面s∈［-5%，5%］，低附著路面s∈［-3%，3%］）。

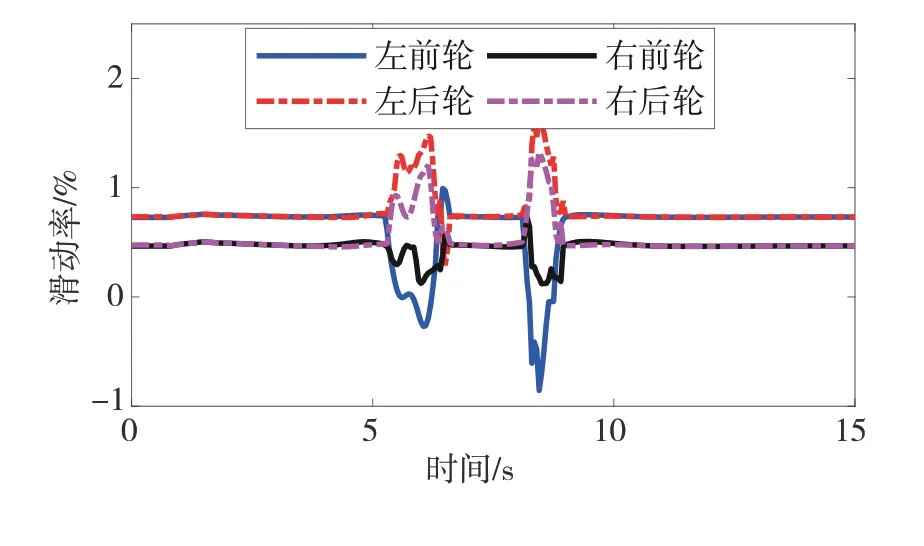
圖13 滑動率仿真結果

4.3 高速雙移線工況驗證

在本文的高速DLC工況中，路面附著系數為0.85，行駛車速為120 km/h。圖14為本文提出的集成控制策略與線性MPC控制器的效果對比。可以看出，與對開路面類似，本文提出的動力學集成控制策略可以在帶有車速變化擾動的高速DLC工況中很好地實現目標軌跡的跟蹤。此工況下產生的路徑跟蹤誤差僅為線性MPC的4.41%。

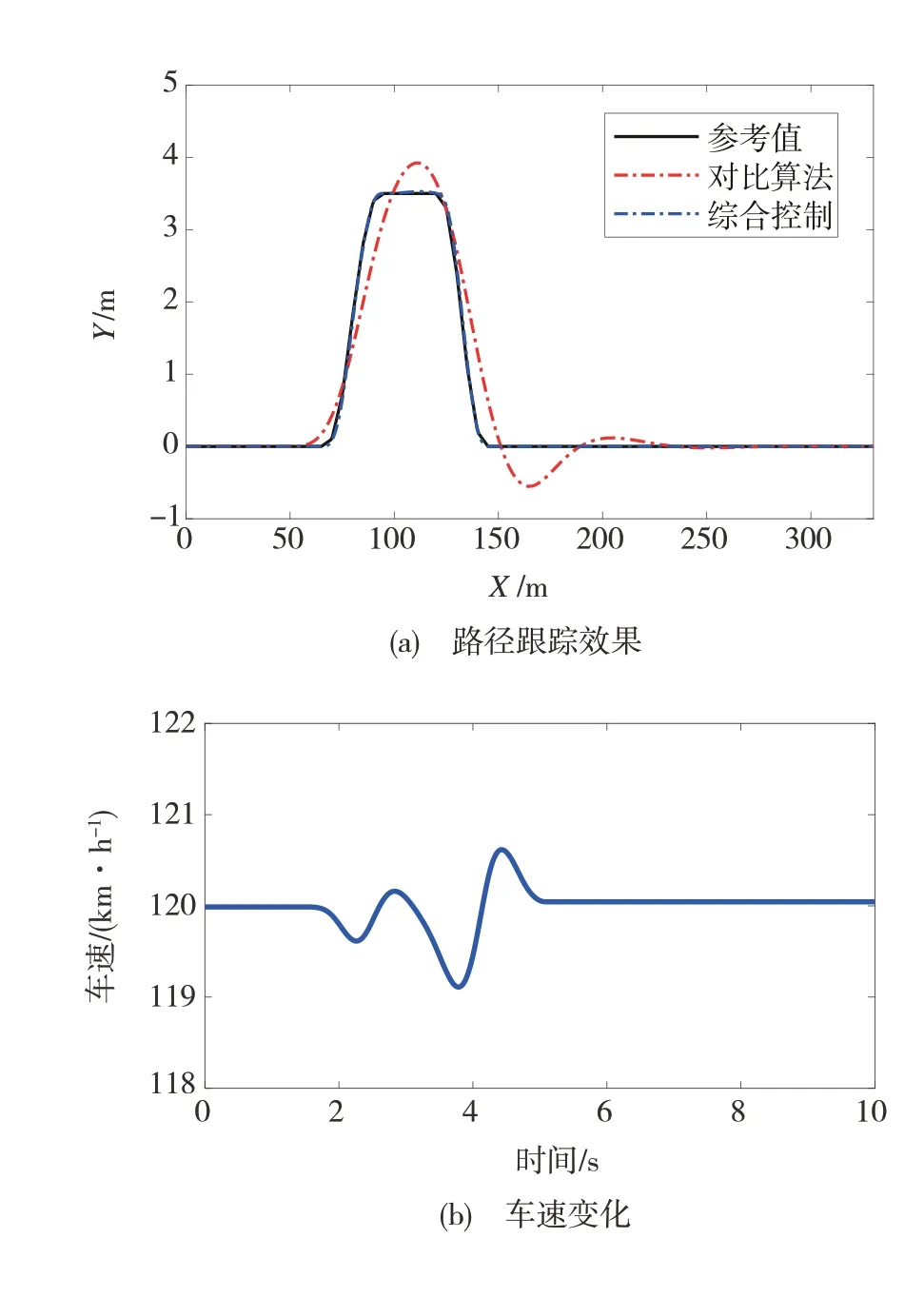
圖14 控制效果對比

圖15展示了控制過程中動力學集成控制策略與對比算法的前、后輪胎側偏角的對比結果。根據圖1所示的PWA輪胎模型可知，在控制過程中，前后輪側偏角均已進入非線性區域，因此，由于線性MPC控制器預測模型中的線性輪胎側向力與實際值產生了較大的差距，其路徑跟蹤誤差明顯大于本文提出的集成控制方法。此外，根據圖5所示的系統分岔點變化規律可知，當車輛在較高的車速下，系統分岔點較小，此時主動轉向角將會更容易達到系統分岔點，AFS+DYC復合控制模式也將會更頻繁地介入，導致集成控制策略產生的前、后輪側偏角因為控制模式的切換出現了波動。

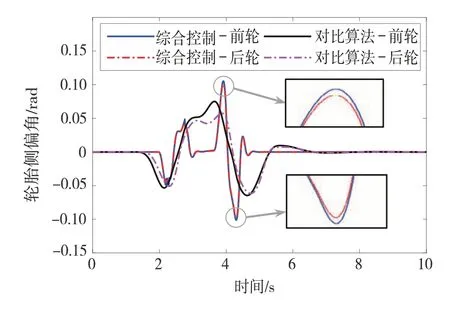
圖15 輪胎側偏角結果對比

圖16展示了高速雙移線工況中動力學集成控制策略計算出的最優輸入。如圖所示，在控制過程中，當車輛在DLC中兩次換道開始、結束的轉向時均將控制模式切換為了AFS+DYC復合控制模式，此時控制模式的切換也導致了圖15中變量的波動。

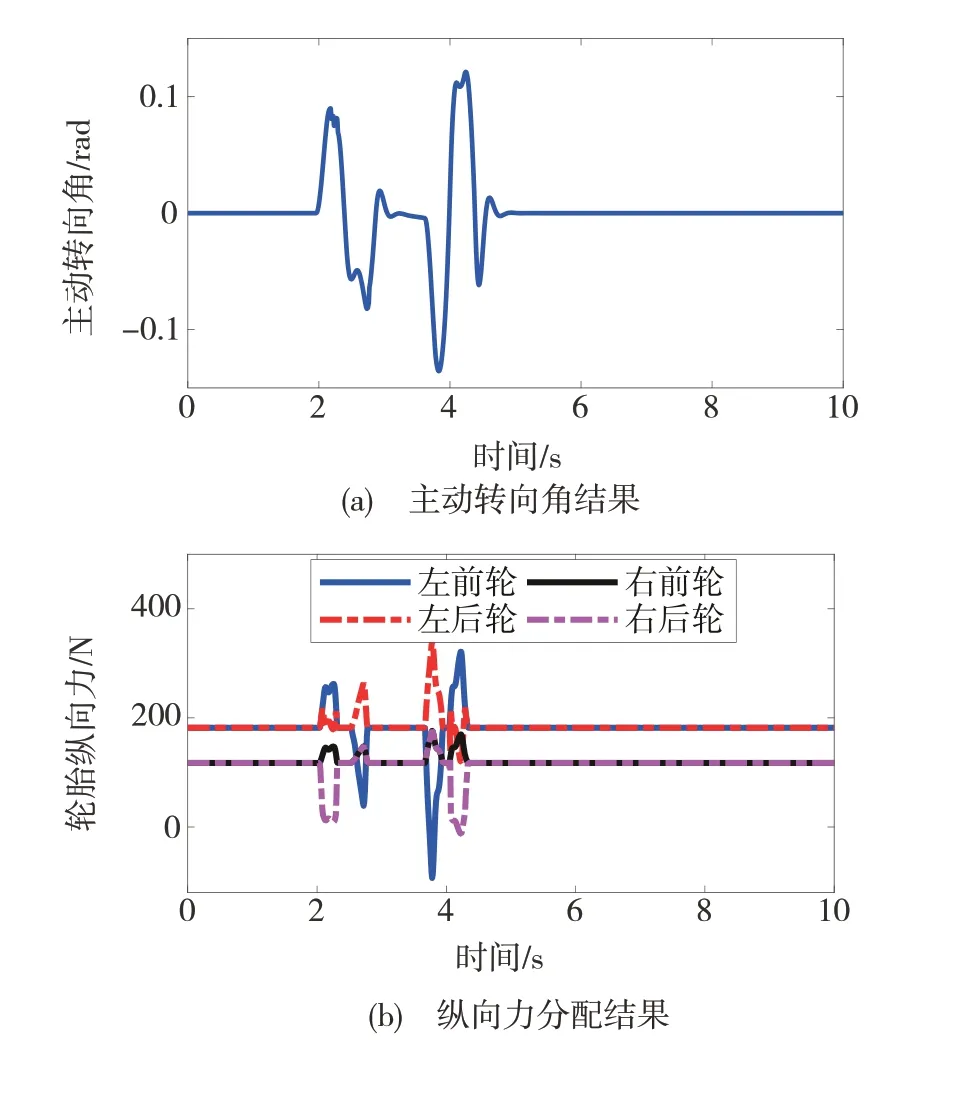
圖16 動力學集成控制最優輸入結果

綜上，本文提出的動力學集成控制方法能夠在低附著路面轉向、高速轉向等易失穩的極限工況下顯著改善車輛的橫擺穩定性，降低路徑跟蹤誤差。

5 結論

為了充分發揮分布式驅動構型的控制靈活性，提高分布式電驅動汽車在極限工況下的主動安全性，本文提出了一種基于魯棒混雜模型預測控制算法的動力學集成控制方法。

（1）建立了分段仿射橫擺動力學模型，均衡了預測模型的建模精度與控制器的計算負擔，基于該方法生成的工程代碼能夠滿足PIL試驗平臺的實時性要求，在50 ms的控制周期內完成有限時域優化問題的求解。

（2）分析了多參數變化條件下的系統分岔行為，將系統分岔點作為極限工況的判別條件，構造了車輛穩定性判據。

（3）提出了基于魯棒混雜模型預測控制算法的動力學集成控制策略，在車速存在有界擾動時仍能保持控制策略的有效性。

處理器在環試驗表明，相比于基于線性模型的MPC橫擺穩定性控制方法，本文提出的動力學集成控制方法在低附著路面行駛與高速轉向工況下可顯著改善車輛的橫擺穩定性，提升了車輛的安全性能。其中，在對開路面DLC工況下，高附著路段平均路徑跟蹤誤差為線性MPC的76.39%，低附著路段僅為線性MPC的3.19%；在高速DLC工況中，整個控制過程的平均路徑跟蹤誤差僅為線性MPC的4.41%。

在后續工作中，將對路面附著條件的快速辨識方法與考慮附著系數擾動的魯棒控制方法開展研究，使本文提出的控制方法能夠實際應用于具有更加復雜多變的路面附著條件的場景中；并研究更精確的不動點計算方法，實現更加精準的非線性系統穩定性分析。