山西某場區地面沉降的灰色理論分析

楊 帥，韓 靜，曹江濤，馬煜棟，王子垚

(自然資源陜西省衛星應用技術中心,陜西 西安 710128)

1 概述

我國最早的地面沉降問題出現于上海市和天津市，隨著地下水的不斷抽取，全國多個地區，包括長江三角洲地區、華北平原、關中平原等地區均存在不同范圍的沉降。目前關于地面沉降原因的研究眾多，概括起來主要包括開發利用地下流體資源、開采固體礦產、巖溶塌陷、軟土的固結沉降、新構造運動、動土融化等因素[1]。而隨著人口的增長和城市建設的飛速發展，地下水超采現象持續嚴重，沉降范圍和幅度逐年擴大。

本次研究地點位于沉降較為突出的太原，該區是重要的人口聚集區，市區屬于典型的黃土分布區，20世紀50年代以來，為滿足居民生活的需求，市區內進行了一系列大規模抽取地下水、礦區開采及排水等活動，對區域工程地質條件造成了極大改變。據研究，太原已形成了五個沉降漏斗區，是我國地面沉降較嚴重的城市之一，并且地面沉降仍處于持續發展狀態[2]。眾多學者對太原市地面沉降原因做出了不同解釋，方鵬飛等[3]認為太原市的地面沉降主要是由于集中開采深層承壓含水層引起的；現今研究認為抽取地下流體時造成地面沉降的主要原因的解釋有兩種：1)有效應力降低原理；2)水動力固結原理[4]。一方面說明抽水使土體的有效應力下降造成含水層的壓實從而引發地面沉降；另一方面解釋了抽水以后的殘余應變引發地面沉降，兩者結合使得黃土顆粒之間的有效應力增加，土層產生固結壓縮，最終導致地面沉降。

以太原某場區地面沉降為研究對象，在為期10個月監測的基礎上，對研究區場地的沉降量進行了統計，然后進行灰色建模處理，預測未來兩個月內沉降量并進行相應的檢驗。檢驗結果表明灰色理論在短期地基沉降預測方面有良好的適應性，對地面沉降預防和治理具有重要意義。

2 沉降模型的建立

通過長期監測發現研究區地面高程位置處于持續下降的狀態，而且沉降規律不明顯，數據相對較少而且具有不確定性，這與灰色系統理論所處理的數據條件基本一致，而且同其他模型相比，該模型結構簡單、適應性強、可信度較高的特點。所以本文借助灰色系統理論對研究區地面沉降進行預測與分析。

2.1 工程概況

太原市位于山西省中部，整體地勢為北，境內地貌類型主要有山地、丘陵、平原、盆地等，具有典型的黃土高原地貌特征。在地質構造上地處山西斷隆的中部，為新生代斷陷盆地，是多個隆起和洼陷地層的交界處，區內構造較為簡單，構造大體呈北東—南西向，被巨厚的松散沉積物所覆蓋。研究區涉及沉降的地層以第三系黃棕色粉砂質黏土、紅黏土以及第四系粉質黏土、沖洪積層為主，綜合厚度超過50 m。該區地處大陸內部，屬于溫帶大陸性氣候。因其位于北半球中緯度地區且為高原地形，所受光照充足，晝夜溫差較大。太原市水資源相對匱乏，大氣降水是水資源的主要補給源，但降水和徑流變化大，分配不均勻水資源緊缺問題嚴重。境內地下水主體可分為基巖裂隙水、碳酸鹽巖類巖溶裂隙水、碎屑巖類裂隙孔隙水和松散巖類孔隙水[5]。太原市礦產資源豐富，以煤、鐵、石膏含量最為豐富。截止到2020年，太原市常駐人口超過500萬人，人口的不斷增長加劇了對地下水以及其他礦產資源的需求，進而影響到地下水系統的平衡以及造成區域生態環境的破壞，對地層的沉降造成巨大影響。

2.2 灰色系統理論

灰色系統理論是由鄧聚龍教授于1982年首次提出的，該理論主要用于解決數據信息不完整，結果不確定性一類問題[6]。灰色系統指系統內部一部分信息已知而另一部分信息是未知的，這種系統是介于系統內部信息完全已知的白色系統和系統內部信息完全未知的黑色系統之間的。而灰色理論模型的主要任務是充分開發和利用為數不多的顯信息和隱信息，進而尋找數據之間存在的數學邏輯和關系[7]。一般情況下，小樣本預測的回歸分析與神經網絡分析效果都不太理想，而灰色預測理論具有適應于數據量較少，數據持續時間相對較短，數據分析過程簡單等特點，完美適合地基沉降分析。所以文中利用灰色系統理論中的一階微分方程GM(1,1)模型進行地面沉降的預測。

設地基沉降監測的歷史數據組成的時間序列為：

x(0)={x(0)(1),x(0)(2),…,x(0)(n)}。

實際上該序列應為一組無規律序列，為了更深一步探討數據之間的規律，需對數據進行灰處理，以便產生新的數據列，發現新的規律。常見的數據生成方法有累加生成、累減生成和均值生成等方法[8]，本次研究中根據數據特征選擇累加生成灰色數據的方式。

x(1)(k)={x(0)(1),x(0)(1)+x(0)(2),…,

x(0)(1)+x(0)(2)+…+x(0)(n)}。

即:

x(1)(k)={x(1)(1),x(1)(1)+x(0)(2),…,

x(1)(n-1)+…+x(0)(n)}。

則x(1)(k)為x(0)的一次累加數列，通過該方法可使任意正向無規律的數列轉化為遞增數列以削弱數據的隨機性。

對于一階微分方程:

其中,a,b均為系數，構造數據矩陣B以及數據向量YN，根據最小二乘法可得：

其中：

YN=[x(0)(2)x(0)(3) …x(0)(n)]T。

將現場實測結果代入對應矩陣及微分方程式中即可求系數a,b的值，然后便得到與沉降相關的微分方程如下：

其預測沉降值為：

模型的預測結果可與實際情況進行直接對比，并可以通過殘差檢驗、關聯度檢驗來確定模型精度。在檢驗分析過程中主要以前八個月的預測和實測數據進行殘差和關聯度檢驗，并以最后兩個月的數據來分析模型的預測情況以及適用性。

2.2.1 殘差檢驗

殘差是指觀測值與預測值之間的差，因此對于每個監測點在不同時刻的預測沉降與實測沉降之間的殘差應是一個殘差序列，而殘差檢驗則是通過數據殘差序列所提供的信息分析數據之間的精確程度和關聯性。

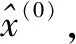
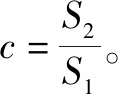
殘差檢驗的重點在于比較預測值與實測值之間差值的大小，其主要由實測值方差以及殘差序列的方差可求得方差比值，此外借助小概率誤差來綜合分析，最后便可根據表1來確定模型精度等級。

表1 灰色模型預測精度表

2.2.2 關聯度檢驗

關聯度是指系統或兩個因素之間的關聯性大小，它反映了系統中因素間相對變化的情況。如果實測值與預測值兩者變化基本一致，則認為兩者關聯度較大；反之。在本次研究的GM(1,1)模型中采用無量綱的關聯度進行精度檢驗，所用的關聯度計算公式如下：

ξ(k)=

其中，ξ(k)為第k個元素的關聯度，ρ∈[0,1]為分辨系數，一般取ρ=0.5，r為所有元素關聯度的平均值，代表整個序列的關聯度大小。多個關聯度實例表明實測數據與預測數據的關聯度越大，模型越好，一般當關聯度大于60%時便可認為兩者的關聯度較高。

3 沉降模型應用

3.1 模型預測

本節根據四個原位監測點在2020年與2021年期間的8個月的沉降統計結果為基礎信息，利用GM(1,1)模型對沉降量進行模擬和預測，然后與2021年3月～4月的實測沉降值進行對比，以便確定模型的適應情況和精確程度。通過監測獲得研究區沉降數據如表2所示。

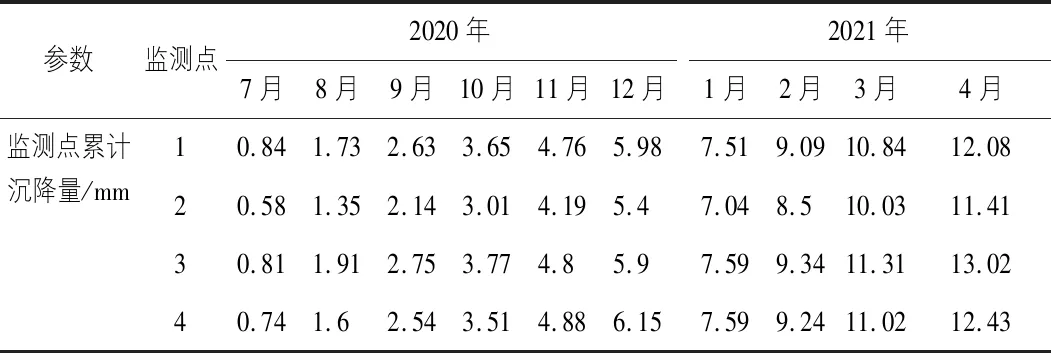
表2 監測點實測沉降量

為了清楚展示灰色模型建立以及預測中的計算和分析過程，本節以監測點1前八個月的實測數據在地面沉降預測中的應用為例，首先對實測結果做累加生成對應x(1)(k)序列見表3。

表3 監測點1累加生成序列

確定矩陣B和YN：

YN=[1.73,2.63,3.65,4.76,5.98,7.51,9.09]T。

那么：

則:

所以監測點1的灰色理論預測模型為：

同理可求出其他3個監測點的預測模型如下：

監測點2預測模型：

監測點3預測模型：

監測點4預測模型：

從預測模型的數學表達式可以看出，該區域的累計沉降量在一定時間范圍內以近似指數遞增的方式變化，并且4個監測點的預測模型數學表達式極為相似，其表達式系數值的差值很小，這也說明在監測點所圍成的區域內部沉降應是同步且均勻發生的。

根據監測點的沉降模型預測公式，給定不同k的值，便可得到不同時間對應的地面沉降值，見表4。

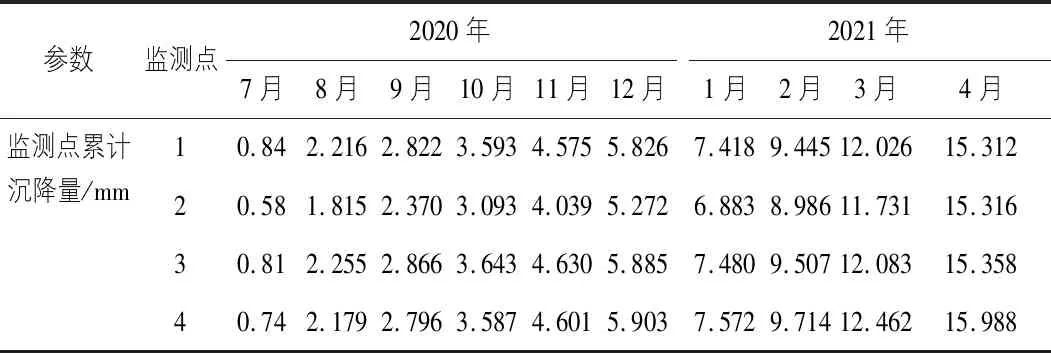
表4 監測點沉降預測值

3.2 模型檢驗

結合實測結果與預測模型，對預測模型的精度等級分別利用殘差檢驗以及關聯度檢驗進行精度分析，在本節以監測點1精度分析為例。

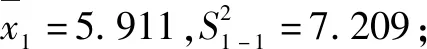
監測點1的殘差序列為ε(0)=[0,0.486,0.192,-0.057,-0.185,-0.154,-0.092,0.355]；

相對誤差序列為：Δk1=[0,0.486,0.192,-0.057,-0.185,-0.154,-0.092,0.355]；

方差比值c1=0.086 5；

小概率誤差：p=1.00；

查表2可以確定出該模型的精度等級為好。

該模型每個元素的關聯度序列為：

ξ(k)=[1,0.333,0.559,-0.81,-0.568,-0.612,-0.725,0.406]。

則關聯度:

r1=0.627。

由此可認為監測點1處的預測沉降值與實測沉降值之間的關聯度較高。

同理可以得出其他3個監測點的精度以及關聯度，4個監測點的精度以及關聯度分析結果如表5所示。

表5 模型精度與關聯度匯總表

表5說明了研究區的預測模型精度和關聯度均達到理想標準，模型對該地區地面沉降的擬合程度較高。結合表4可以發現，由前8個月的實測數據求得的預測模型與實測結果之間的殘差較小，模型對已知沉降的模擬精確程度較高。通過比較第9個月的沉降值發現，模型對沉降的預測較為準確，其誤差不足10%，但對第10個月的預測誤差逐漸增大，已經接近25%。由此不難推測當時間不斷增加時，模型的預測精度會逐漸降低，這也符合指數函數隨著因變量的增加，其函數值增加的速度越來越快的特點。這也表明灰色理論預測模型的適應時間段有限，但在有限的時間段內其預測結果精度較高。

3.3 殘差修正

為了進一步提升灰色理論預測模型的精確程度，并降低預測過程中出現的較大誤差的可能性，對預測模型進行殘差修正。本節仍以監測點1的數據為例。通過前面分析，已知監測點1的殘差序列為：

ε(0)=[0,0.486,0.192,-0.057,-0.185,-0.154,-0.092,0.355]。

其中殘差序列中最小值小于0，因此對殘差數列進行正向平移變化，本節中對殘差數列所有數據加1，使得序列中每一項均為正數，并得到新的數列:

ε(1)=[1,1.486,1.192,0.943,0.815,0.846,0.908,1.355]。

對該數列進行灰色理論預測可得：

對模型1進行修正得：

同理可得其他3個監測點的修正模型為：

通過對比殘差修正模型預測結果與實時監測結果，發現殘差修正模型在一定程度上提高了預測模型的精度，但仍然存在著當時間序列增加，其預測結果偏移量增加的情況，所以灰色理論預測模型只適用于短期且已知信息量較少的數據變化趨勢預測。

3.4 沉降改善措施

受地表水資源匱乏的制約因素，太原地區需要大量地下水開采來保證社會經濟正常發展，且無法像長三角平原、江漢平原等地區由于地表水資源豐富，而采用地下水禁采措施減少沉降。目前太原地區沉降改善措施主要有以下幾個方面：

1)減少在同一地方大量進行地下水開采而導致地下水位下降過大，應采用分布式開采，減輕局部地區開采壓力，有助于減少區域性的地面沉降。

2)由于深層地下水不易得到補給，恢復較慢。因而考慮開采恢復能力較強的淺層地下水(潛水含水層與微承壓水)，降低潛水位有利于減少地下水蒸發量，增大地表水向下入滲并可加速淺層水循環，有利于污染淺水層的修復。太原地區開采水資源應注重大氣降水與地表水的獲取，從而減少地下水開采壓力。

3)對于水源地的規劃應采取多且分散的規劃策略，按照各個水源地的具體情況可以適當的進行輪流開采，將水位情況作為可開采資源的必要約束條件。將主要的湖泊、河流附近進行水源地的規劃開發作為地下水開采的合理補充。并對其做好保護工作，防止其受到污染影響。

4)加強地下水水位的動態監測，地面沉降一般滯后于水頭的下降,前期變形緩慢很難察覺，一旦發生很難恢復，對于其動態實時監測尤為重要，地下水水位與地面沉降觀測網絡包括地下水觀測井和基巖標以及分層沉降標的合理規劃與統一管理尤為重要。其為最大限度獲取實時地下水與地面沉降的動態資料扮演著關鍵性角色。

5)星載合成孔徑雷達干涉測量(InSAR)技術由于空間覆蓋范圍廣、空間分辨率高、全天時、全天候、形變探測精度高等特點，成為常用大地測量技術之一，通過計算兩次過境時SAR影像的相位差來獲取數字高程模型。相比GPS測量、常規大地測量法和近景攝影測量等傳統方法,具有毫米級的監測精度，作業效率高、數據處理流程化等優勢。對于城市地面沉降，礦山沉降形變監測，基礎設施沉降監測在近年來廣受追捧，并且隨著SAR衛星的成像質量和時空分辨率等越來越高，其監測效果也愈加增強，對于地面沉降毫米級形變的實時監測預警，可以幫助第一時間發現沉降區域，在沉降初期進行治理工作，降低沉降對城市帶來的威脅，目前InSAR技術對于沉降發生的預警作用已在各地廣泛開展應用。

4 結論與討論

地面沉降是多種外部因素和內部因素綜合作用的結果，現有理論很難解釋地面沉降的過程。而地面沉降量的統計、計算和預測在某種程度上是一種信息相對模糊，既存在部分已知信息又具備部分未知信息的一種系統。所以可利用灰色系統理論對地面沉降量進行短期預測以便應用于實際工程。本文為對四個監測點的沉降量進行灰色理論模型分析，推導出了研究區的地面沉降在短期內的預測公式，得到主要結論如下：

此次研究只是GM(1,1)模型的一種應用，對于類似問題也可以采用GM(1,n)模型來解決。模型在預測短期地基沉降方面具有較高的精確性，研究在區及其附近范圍內適用性較強，對于今后區域內沉降的監測和指導工程施工具有積極的意義。

通過對比四個監測點的預測模型公式，可知該區域的預測模型相似度較高，可初步推測在監測點所圍成研究區內發生的是一個整體上的均勻沉降，在該區域內各處的沉降趨勢基本上是一致的。

從極限分析的角度來看，地面沉降在時間間隔發展到一定階段后終會停止，甚至出現回升，而模型預測的沉降量是一個持續增加的數值，這造成模型在短期內的預測精度較高，而長期預測的地面沉降值精度有所下降。因此對于時間間隔較長的地面沉降，還需重新統計沉降發生的近期數據并開展新的預測。