m-NOD樣本最近鄰密度估計的相合性

王 巍，劉子湘

（池州學院，安徽 池州 247000）

0 引言

設總體X的密度函數和分布函數分別為f(x)和F(x)，X1,X2,X3,…,X n是取自于總體X的樣本。又設{k n,n≥1}是選定的正整數序列，滿足1≤k n≤n，a n(x)為最小的正數a，使得[x-a,x+a]中至少包含X1,X2,X3,…,X n中的k n個。Loftgarden和Quesenberry［1］將f(x)的最近鄰估計定義為

最近鄰密度估計是一種較常用的非參數概率密度估計方法，目前已取得許多研究成果。在相依樣本方面，Boente和Fraiman［2］研究了基于φ-混合和α-混合樣本的最近鄰密度估計的強相合性；Chai［3］得到了基于φ-混合平穩過程的最近鄰密度估計的強相合性、弱相合性、一致強相合性及其收斂速度；Liu和Zhang［4］建立了φ-混合樣本的最近鄰密度估計的相合性和漸近正態性；Yang［5］研究了負相關（NA）樣本的最近鄰密度估計的弱相合性、強相合性、一致強相合性；Wang和Hu［6］將Yang［5］的結果從NA樣本推廣到WOD樣本。基于上述文獻，本文將進一步研究m-NOD樣本的最近鄰密度估計的弱相合性、強相合性和一致強相合性。

Joag-Dev和Proschan［7］提出了NOD隨機變量的概念，它是一類非常普遍的相依結構，包含了獨立隨機變量、NA隨機變量。許多學者研究了NOD隨機變量的概率極限定理和統計大樣本性質［8-14］。基于NOD隨機變量，Wang等［15］引進了m-NOD隨機變量的概念。設m≥1為固定整數，若任意n≥2和對于所有的1≤k≠j≤n，Xi1,X i2,...,X i n是NOD隨機變量，則稱{X n,n≥1}是m-NOD序列。Joag-Dev和Proschan［7］證明了NOD隨機變量包含了NA隨機變量。Hu和Yang［16］證明了NOD隨機變量包含了NSD隨機變量。由此可見，m-NOD隨機變量包含了獨立隨機變量、NA隨機變量、NSD隨機變量以及NOD隨機變量。因此，研究m-NOD隨機變量的大樣本性質具有重要的理論意義。

本文利用m-NOD序列的性質與Bernstein不等式，進一步研究m-NOD樣本最近鄰密度估計的相合性，推廣和改進已有文獻的結果。為行文方便，假設C為一個正常數，在不同的地方可以表示不同的值；除非另有說明，否則極限取表示不超過x的最大整數值，c(f)表示函數f的所有連續點，logx=ln max(x,e)。

1 引理與主要結果

為了獲得本文的主要結果，首先給出以下幾個引理。

引理1.1［15］設{X n,n≥1}是m-NOD隨機變量序列，若{f n(?)，n≥1}均為非增（或非降）函數，則{f n(X n)，n≥1}也是m-NOD隨機變量序列。

其中，對于每個1≤l≤m，{X mi+l，0≤i≤j}是NOD隨機變量。故由引理1.2可得

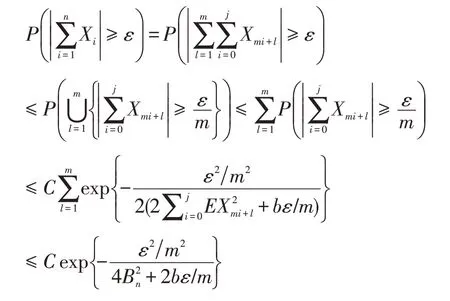
由此得到結論，證畢。

引理1.4［5］設F(x)為連續分布函數，對于n≥3，假設x nj滿足F(x nj)=j/n,j=1,2,...,n-1，那么

下面給出本文的主要結果。

2 主要結果證明

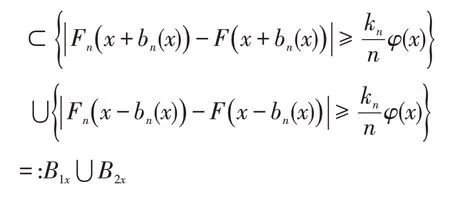
同理，由式（3）和式（5）可得

定理1.1證明完畢。

由此推論1.1得證，證畢。

定理1.3的證明 證明將沿用定理1.1證明中的記號。由于f(x)是一致連續的，可推導出對于任何ε>0，存在一個正常數δ0，如果|x-y|<δ0，有

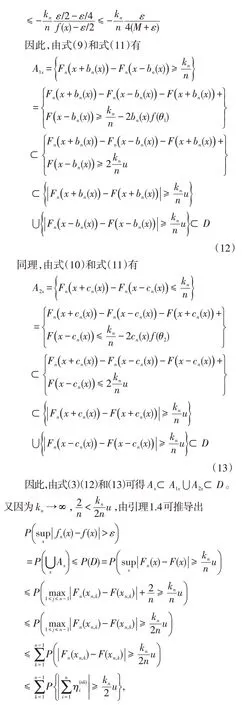
3 結語

本文首先建立了m-NOD序列的Bernstein不等式，利用m-NOD序列的性質和Bernstein不等式，研究了m-NOD樣本的最近鄰密度估計的弱相合性、強相合性及一致強相合性，將最近鄰密度估計從NA樣本推廣到更一般的m-NOD樣本，進一步拓展了最近鄰密度估計的應用范圍，為最近鄰密度估計方法應用在更普遍的相依結構數據上奠定了理論基礎。