航空發動機軸承故障結構化貝葉斯稀疏表示

張爍,劉治汶

電子科技大學 自動化工程學院,成都 611731

主軸承是航空發動機所有零部件中最為關鍵的部件之一,其工作環境完全可以用“煉獄”來形容,它們長期在高溫、高壓、高轉速等惡劣條件下運行,并承受各種交變應力載荷的作用,導致故障頻發,如：CFM56-3發動機高壓壓氣機主軸承失效占發動機空中停車事件的25%,在各種故障中居首位；外場使用統計表明,我國某型號發動機主軸承失效造成的飛行事故占機械系統總故障的19%左右。因此,主軸承失效已歸納為航空發動機的八大故障之一,其質量好壞直接影響到航空發動機的使用可靠性和安全性。

主軸承振動監測診斷技術是保障航空發動機運行安全的關鍵技術之一。美國VAATE計劃將先進的振動監測診斷與主軸承狀態監測技術列為PHM診斷關鍵技術；美國F119和F135發動機都采用前中介機匣、后支承環以及附件機匣3個振動加速度傳感器監測發動機振動信息。但航空發動機主軸承位置分布廣,由于空間位置等限制,測振傳感器無法安裝于軸承座上,而是一般安裝于發動機機匣上。主軸承至測振傳感器之間部件多,主軸承激起的振動通過軸承座、靜子承力系統及機匣傳遞后被測振傳感器獲取,信號傳遞路徑復雜,具有強時變非平穩特性,且背景噪聲強烈,難以及時有效地診斷。

非平穩噪聲的有效抑制一直是受研究者關注的問題,2006年壓縮感知理論的提出為在信號處理領域中應用稀疏表示理論做了鋪墊。稀疏表示通過計算每次迭代后逼近信號的峭度值,找出峭度值最大時對應的逼近信號,自適應確定特征成分與噪聲成分的稀疏分解分界點,具有良好的抗噪能力和微弱狀態成分提取能力。近年來,以正交匹配追蹤(Orthogonal Matching Pursuit, OMP)算法為代表的稀疏表示貪婪類及其改進算法,對小尺度信號具有重構速度快、運算量小等優點,但這種方法只考慮了信號整體的稀疏性,往往會造成低信噪比條件下難以精確重構信號的問題。針對以上缺陷,文獻[12]提出貝葉斯快速匹配追蹤(Fast Bayesian Matching Pursuit, FBMP)算法,通過建立噪聲條件下用于識別稀疏信號非零元素下標的貝葉斯假設檢驗模型,剔除匹配追蹤(Matching Pursuit, MP)算法輸出支撐集的冗余下標,得到了更好的重構性能和抗噪能力,但是該算法采用MP算法預重構,重構效率較低。針對文獻[13]的問題,Herzet和Drémeau提出了貝葉斯正交匹配追蹤(Bayesian Orthogonal Matching Pursuit, BOMP)算法,該算法利用OMP算法代替的MP算法對原始信號進行粗重構,以提高運算效率,將重構輸出的支撐集作為候選集；然后利用貝葉斯檢驗模型對候選集中的原子進行篩選,去除候選集中的冗余原子,由于該算法可明顯減少冗余支撐集,因此算法重構運算量上可明顯減少,重構和抗噪性能明顯增強。但BOMP要求預先了解信號及噪聲的先驗概率密度函數,未考慮結構性干擾可能造成的影響,導致算法求解效率較低；并在更新參數中采用期望最大化方法,導致運算量大,這大大局限了該算法的應用范圍。因此,如何將結構信息作為先驗,約束所構造冗余字典的更新,更好的捕捉信號本身的固有特性,提高信號結構化稀疏重構算法的性能需要進一步研究。

另一方面,稀疏分解算法在處理基于冗余字典的重構問題時,由于冗余字典中原子過多,而匹配過程需遍歷字典中所有原子,計算復雜度高。考慮到智能進化算法的搜索復雜度與字典大小無關的優點,學者們將遺傳算法(Genetic Algo-Rithm, GA)、粒子群優化(Particle Swarm Opti-Mization, PSO)等及其混合算法應用于圖像和信號的稀疏分解,降低計算復雜度,使稀疏分解的速度得到有效提高。但上述智能進化算法也存在明顯不足,有時容易陷入局部優化而得不到全局最優,收斂速度慢,精確度有待提高。灰狼優化(Grey Wolf Optimization, GWO)算法模擬了自然界中狼的狩獵方式,抽象出了狼的搜索、圍攻和更新這3種智能行為。與粒子群算法和遺傳算法相比,GWO具有敏感參數少、魯棒性強、收斂速度快、精度高等優點。

綜上所述,本文提出一種參數優化字典的結構化貝葉斯正交匹配追蹤(Structed Bayesian Orthogonal Matching Pursuit, SBOMP)稀疏表示的航空發動機軸承故障診斷方法。首先,基于貝葉斯概率模型,在BOMP算法基礎上,研究了一種能促進稀疏重構效果的結構化貝葉斯正交匹配稀疏表示模型,實現對信號的稀疏表示求解。其次,根據軸承故障振動信號特性,設計了時頻沖擊字典原子,并將GWO算法引入基于時頻沖擊字典的SBOMP模型中,在迭代過程中選擇與剩余信號匹配的最優原子,并在重構算法中引入閾值降噪,提高信號稀疏表示的效率和精度；最后,將上述算法應用于航空發動機滾動軸承故障試驗信號分析中,結果證明了算法的有效性。

1 結構化貝葉斯正交匹配追蹤

航空發動機軸承的特征提取是通過處理和分析由故障引起的振動信號來進行的。稀疏表示旨在將故障振動信號描述為從一個過完備字典中選擇的少量基本信號或原子的組合。

(1)

討論一般概率模型中的結構化稀疏表示問題并提出一種新的匹配追蹤算法,該算法尋找聯合極大后驗(MAP)問題的解,并通過玻爾茲曼機實現了支撐體原子間的相互連接。該算法是對貝葉斯正交匹配追蹤(BOMP)算法的推廣。

定義∈{0, 1}為稀疏表示支持度的向量。在不失一般性的情況下,通過下列公約定義：如果=1(或者=0),的第列會(或者不會)被用于產生。用表示的第列,然后考慮觀測模型：

(2)

式中：為零均值、方差為的高斯白噪聲。則：

(|,)=(,)

(3)

(4)

根據參數和服從玻爾茲曼機分布：

()∝exp(+)

(5)

式中：∝表示歸一化因子相等性；為一個對角線上有0的對稱矩陣(用表示的第行和第列的元素)。因此,在模型式(3)～式(5)中,觀測到的可以看作是由指定的有噪聲的原子組合,組合的權值由高斯分布實現,其方差與的支持無關。選擇=0×結果為伯努利模型：

(6)

通過這樣的概率框架,從貝葉斯的角度處理稀疏表示問題。只要式(3)～式(5)是觀測的真實生成模型,就可以在不同的貝葉斯準則(均方誤差、平均絕對誤差等)下得到最優估計量：

(7)

(8)

(9)

(10)

式(8)必須指定更新的元素的索引。選擇更新促使目標函數增長最大的索引,即

(11)

式(9)的解決方案為

(12)

(13)

(14)

(15)

SBOMP的支持更新方程為

2)裝卸。新鮮果蔬鮮嫩，含水量高，如裝卸搬運中操作粗放、野蠻，就會導致商品機械損傷、腐爛，造成巨大的經濟損失。我國果品蔬菜多為人工裝卸搬運，其勞動強度大，機械傷嚴重。裝卸時要求箱子要捆實扎緊，搬運要輕拿輕放，快裝快運。

(16)

SBOMP系數更新式(10)的顯式表達式為

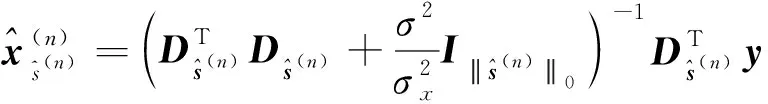
(17)

(18)

最后,更新殘差：

(19)

2 基于灰狼優化算法的時頻沖擊字典

2.1 時頻沖擊字典[18]

實現SBOMP算法的一個關鍵步驟是構造原子字典,使信號在稀疏分解時能夠更好地匹配原子。原子字典的構造直接影響待分析信號的稀疏表達。基于參數化函數模型的原子字典構造方法是最常用的方法。在這種方法中,一個特定的基元函數被離散地參數化(例如,時間、頻率、收縮、平移、調制等)。每個參數組對應一個原子,原子集合構成原子字典。由于通常機械系統的沖激響應可表示為負指數函數與正弦函數的乘積,時頻沖擊字典原子具有包含負指數函數的特點,與信號中的沖擊分量吻合較好。為了有效地提取信號中豐富的特征信息,根據信號的結構特征,構建了一種時頻沖擊字典：

=

(20)

式中：時頻沖擊字典中=(,,,,)為原子參數組；為比例因子；為阻尼系數；為位移因子；為頻率因子；為相位因子；為時間。

根據待分析信號的特性,確定原子參數的范圍。在SBOMP算法迭代中,一旦指定了每個原子參數的范圍,根據式(14)和式(15)可以得到與分析信號匹配的最優原子。

2.2 灰狼優化(GWO)算法[17]

為了在設計GWO時對狼的社會等級進行數學建模,將最優解作為,第2和第3個最優解分別命名為和。剩下的候選解為,在GWO算法中,狩獵(優化)由、、引導,狼跟隨這3只狼。

2) 圍捕獵物

為了建立圍捕行為的數學模型,建立方程：

(21)

(22)

(23)

(24)

3) 狩獵

灰狼有識別獵物位置并將其包圍的能力。狩獵通常由引導,和偶爾也會參加狩獵活動。為了從數學上模擬灰狼的捕獵行為,保存到目前為止獲得的前3個最佳解決方案,并要求其他搜索個體(包括)根據最佳搜索個體的位置更新其位置：

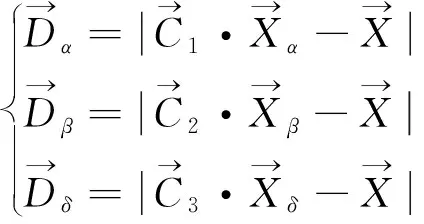
(25)

(26)

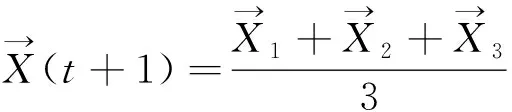
(27)

4) 攻擊獵物(利用)

5) 搜尋獵物(探索)

圖1呈現出了4種不同優化算法的平均適應度值的最小均方誤差(MSE)對比。設置相同的迭代次數50次,種群數量30。MSE結果通過對數表示呈現。從圖中可以清晰地看出,GWO的收斂精度明顯優于遺傳優化算法(GA)、人工蜂群優化算法(ABC)、粒子群優化算法(PSO)。

圖1 優化算法適應度對比Fig.1 Comparison of optimization algorithm fitness

3 結構化貝葉斯正交匹配追蹤 (SBOMP)稀疏表示模型

時頻沖擊字典中包含4個參數,而稀疏表示最主要的困難就是尋找最優原子。因此,GWO算法用來優化字典參數來尋找和故障信號最匹配的原子。所提方法的整體流程圖如圖2所示。所提方法具體步驟為

輸入待分析軸承振動信號,設置GWO迭代次數、個體數、SBOMP迭代次數。

獲得初始剩余信號,同時根據輸入待測信號的特性確定原子參數范圍。

通過式(14)使用GWO算法獲得最匹配原子。

更新稀疏表示支持集和稀疏表示系數。

更新剩余信號,并確定是否達到SBOMP最大迭代次數。如果達到,輸出重構信號；如果未達到則返回步驟3。

圖2 所提方法流程圖Fig.2 Flowchart of proposed method

4 仿真分析

為了驗證方法的有效性,仿真模擬軸承外圈故障,其模擬的故障周期性沖擊信號表達式為

(28)

式中:和分別為尺度因子和阻尼系數；=2π,為軸承的正常運轉頻率。其中、、分別取為5、0.1、3 000 Hz,沖擊重復周期0.01 s。仿真信號的采樣頻率為10 kHz,采樣點數為4 096,如圖3(a)所示。將仿真信號疊加高斯白噪聲信號(噪聲強度=06,如圖3(b)所示),得到合成信號,如圖3(c)所示。采用GWO-SBOMP方法處理合成信號,設置時頻沖擊字典的4個參數范圍如下：∈[0.3,0.5],∈[128,512],∈[0,6 000],∈[0,2π]。

圖3 仿真輸入信號Fig.3 Simulated input signal

仿真設置灰狼優化OMP模型和無優化算法的SBOMP模型作為對比,灰狼優化算法最大迭代次數和個體數分別為10和30。SBOMP的最大分解次數為45,通過對比獲得的重構信號如圖4 所示。

圖4 不同稀疏表示算法仿真結果對比Fig.4 Comparison of simulation results of different sparse representation algorithms

對于加了高斯白噪聲的仿真信號,由于缺少對故障信號結構性的判斷,通過無優化OMP模型稀疏重構的結果會導致部分故障沖擊缺失,同時最佳匹配原子不能精準匹配故障特征信號。另外,無優化算法的SBOMP模型重構的結果雖然保留了更多的故障沖擊特征,然而缺少了優化算法對字典的參數優化,不僅導致了部分故障特征無法提取,同時部分最優原子產生了諧波特性,無法匹配故障的沖擊信號。通過圖4(c)、圖4(d)和圖4(e)的對比,可以看出灰狼優化算法更準確的選擇了SBOMP字典參數,使重構信號的幅值與仿真輸入信號幅值近似程度更高,保障了重構信號的精度。因此,本文所提的方法不但可以重構出信號,而且重構精度很高,可以在同樣的重構次數中準確的重構出有效信號,遺留下更多噪聲信號作為剩余信號。同時,因為時頻沖擊原子字典的優點,所提出的參數優化字典的結構化貝葉斯稀疏表示方法在混合信號重構方面具有很大的優勢。

通過以上分析和比較,證明了本文方法的有效性和優越性。該方法能充分的重構軸承故障信號,表明在軸承故障信號中含有一定成分的噪聲情況下,該方法仍能有效的提取軸承故障特征。

5 實驗驗證

為進一步驗證文中提出方法的可行性,通過航空發動機轉子系統中滾動軸承實驗數據對所提方法進行工程驗證。

5.1 滾動軸承實驗介紹

航空發動機轉子系統軸承故障數據來源于南京航空航天大學智能診斷與專家系統室。試驗臺包括調速電機、齒輪箱、轉子系統等裝置,并通過加速度傳感器采集待測軸承處加速度信號,如圖5所示。待測滾動軸承設置了外圈、內圈故障,如圖6所示。測試軸承相關參數如表1所示。

圖5 滾動軸承試驗臺Fig.5 Rolling bearing test bench

圖6 外圈和內圈故障的滾動軸承Fig.6 Rolling bearing with outer race fault and inner race fault

表1 滾動軸承幾何尺寸Table 1 Rolling bearing geometry

5.2 滾動軸承外圈故障信號分析

軸承外圈故障實驗中轉頻為=30.86 Hz,采樣頻率為10 kHz,由此可計算出外圈故障頻率為=79.4 Hz。軸承外圈故障原始振動信號的時域圖和頻域包絡譜如圖7所示,從圖7(a)中振動信號時域圖中可以看出時域波形雜亂,沒有明顯的故障周期性沖擊信息,僅在頻域包絡譜中能夠找到外圈故障特征的1倍頻率。

圖7 軸承外圈故障實驗原始振動信號Fig.7 Original vibration signal of bearing outer race fault experiment

利用所提方法對外圈故障信號進行分析,得到重構信號的時域波形、剩余信號波形和重構信號頻域包絡譜如圖8所示。其中,字典參數范圍設定為：∈[0.01,1],∈[0,16],∈[0,600],∈[0,2π]。

通過分析,在圖8(a)中能清晰看到所提方法保留了信號的周期性沖擊成分信息,圖8(b)中出現周期性等間隔沖擊=0.012 6 s,即79.4 Hz,對應軸承外圈故障特征頻率。在圖8(c) 中可以看出,剩余信號的幅值限制在0.4以內,驗證了本文方法可以得到高信噪比的重構信號。通過圖8(d)能清楚的找到故障特征頻率的1倍頻率及倍頻(2和3),還能夠找到其外圈轉頻信息；進一步對比圖7(b)和圖8(d) 發現,采用本文所提方法能夠增強故障特征能量幅值,使分辨率提升。

圖8 軸承外圈故障實驗振動稀疏重構信號Fig.8 Vibration sparse reconstruction signal of bearing outer race fault experiment

進一步驗證本文所提方法的優越性,采用快速峭度圖(Fast Kurtogram, FK)方法進行對比分析, FK篩選出最佳頻帶(對應圖9(a)中紅色框處)的中心頻率為3 125 Hz,帶寬為416.67 Hz。對分解頻帶進行濾波解調,得到濾波信號和對應包絡譜如圖9(b)所示。由圖9(b)可以看出,帶通的濾波信號不能看出周期性沖擊現象,包絡譜中可找到故障特征頻率的1倍頻率及倍頻(2和3),但其結果中存在較多的邊頻噪聲干擾。與FK方法相比,本文方法去噪效果較優,更適合滾動軸承故障診斷。

圖9 快速譜峭度法分析外圈故障結果Fig.9 Fast kurtogram analysis of outer race fault results

5.3 滾動軸承內圈故障信號分析

軸承內圈故障轉頻為=17.6 Hz,采樣頻率為10 kHz,內圈故障頻率為=78.125 Hz。圖10(a)和圖10(b)為被測軸承內圈振動信號的時域圖和頻域包絡譜。圖10(a)中原始波形難以分辨出故障周期沖擊特征,圖10(b)中包絡譜的高頻噪聲占比較大,軸承內圈缺陷的低頻特征淹沒于強噪聲背景中,未能找到內圈故障頻率及其倍頻存在。

圖10 軸承內圈故障實驗原始振動信號Fig.10 Original vibration signal of bearing inner race fault experiment

利用圖2所示方法對內圈故障信號開展分析,得到圖11(a)～圖11(c)所示結果。從圖11(a)中可以看出,本文所提方法能將軸承損傷的沖擊信息都提取出來,圖11(b)中存在周期性沖擊間隔=0.012 8 s,對應軸承內圈故障特征頻率78.125 Hz；在圖11(d)能清楚的找到故障特征頻率的、2和3,并且也能夠找到其轉頻；從圖11(c)中可以看出,本文方法剩余信號的幅值限制在0.4以內,同樣得到高信噪比的重構信號。通過對比圖10(b)和圖11(d)可以發現,本文所提方法依然能夠明顯增強故障特征能量幅值,且分辨效果更加清晰。

同樣,采用FK方法對試驗數據分析處理。所得到的快速峭度圖如圖12(a)所示。FK方法所定位的分解帶對應圖12(a)中的紅色框處(中心頻率為4 791.67 Hz,帶寬為416.67 Hz)。分解帶所得到的濾波信號及其對應的包絡譜如圖12(b)所示。由圖12(b)可以看出,帶通的濾波信號不能看出周期性沖擊現象,包絡譜中能找到故障特征頻率的1倍頻率及倍頻(2),但其分析結果中仍存在較多的邊頻噪聲干擾。與FK方法相比,本文所提方法同樣具有更好的去噪效果,進一步驗證了該方法在航空發動機軸承故障特征提取中的有效性和適用性。

圖12 快速譜峭度法分析內圈故障結果Fig.12 Fast kurtogram analysis of inner race fault results

6 結 論

1) 針對傳統的稀疏表示方法都是假定稀疏表示系數是隨機分布的,沒有考慮到信號稀疏表示向量中任何隱藏的結構。因此,基于貝葉斯概率模型,研究了一種能夠促進稀疏重構結果的結構化貝葉斯正交匹配追蹤(SBOMP)稀疏表示模型,該模型對稀疏信號的結構化具有一定的約束能力,反映隱藏在信號數據中的結構,提高了稀疏系數求解的精度。

2) 從本質上來講,結構化貝葉斯正交匹配追蹤稀疏表示還是屬于貪婪迭代算法,在對信號的每一次迭代分解中,都要通過繁重的內積運算以求最匹配的原子,因此計算量還是過大。針對該算法計算量大的問題,利用灰狼優化選擇最佳的時頻沖擊字典原子,降低計算復雜度。由于灰狼優化的多參數空間具有連續性,使得搜索空間的原子量更大,結果能更好的匹配提取出振動信號中的故障沖擊成分,使得信號的表示更稀疏。

3) 結構化貝葉斯正交匹配追蹤稀疏表示能夠通過求解時頻沖擊字典下信號的最稀疏表示可以有效地去除振動信號中的強背景噪聲,較好地體現出周期性沖擊的故障特征,提供了一種稀疏表示框架下非平穩信號消噪的新方法,可應用于航空發動機軸承故障診斷。