轉頻調制下齒輪泵壓力脈動機理

許文綱,王志穎,孫闖,嚴如強,陳雪峰

西安交通大學 機械工程學院,西安 710049

航空發動機作為飛機的“心臟”、動力之源,是一種集結構、材料、制造、液壓、氣壓、熱工、電子、控制等眾多尖端技術于一身并運行于高轉速、高溫、重載、強擾動等極端服役環境下的高科技、高附加值的高精密復雜機械產品,被譽為現代工業“皇冠上的鉆石”,是中國航空工業的瓶頸,嚴重制約著中國軍用、民用先進飛機的發展。燃油控制系統被譽為發動機的“心臟”,其中主燃油泵是燃油控制系統的核心元件,重要性不言而喻。據統計1986—2004年間發生的387起燃油控制系統故障中,主燃油泵發生故障高達66起,其中54起液壓管路故障也是由主燃油泵故障引起的,因此對主燃油泵性能進行研究具有重要意義。齒輪泵作為主燃油泵的重要組成部分,因其結構緊湊、體積小、重量輕、價格低廉,對油液污染敏感度低,自吸性能好而廣泛應用于電力、汽車、冶金、軍工、航空、航天和化工等各個機械行業,同時也有自身的缺點比如：齒輪所受的徑向壓力不平衡、軸承容易磨損、流量均勻性差、壓力脈動大、振動大、噪聲大等。國內外學者針對齒輪泵壓力脈動從機理、齒輪泵結構參數優化、軟件仿真、實驗等方面進行了大量的研究。柏宇星等采用流場分析軟件CFX對齒輪油泵內部流場進行三維非定常計算,通過設置監測點,得到不同位置的壓力脈動結果,實驗表明主動齒輪齒腔壓力脈動要高于從動齒輪,齒頻是影響壓力脈動的主要因素。張鑫用AMESim軟件建立了齒輪泵的功能模型,并仿真得到壓力脈動數據,然后用神經網絡計算得到的脈動數據與仿真得到的數據進行比較。陳中華等利用平穩小波分解與重構將壓力信號的低頻波動項與高頻脈動項進行了分離, 并對低頻波動和高頻脈動部分的功率譜進行了分析,得到工頻可作為齒輪磨損故障的特征頻率,對輪齒磨損做出診斷。阿巴沙分析了壓力脈動機理,運用外嚙合齒輪泵錯相位并聯方法和外嚙合齒輪泵閉環伺服控制方法來減小脈動。喻開清通過研究齒輪泵流量脈動機理的數學模型,得到了齒輪各參數對流量脈動的影響,并通過遺傳算法優化齒輪泵參數以達到減小流量脈動的目的。Mancò和Nervegna建立了齒輪泵準穩態數學模型的微分方程。該模型在預測出口壓力脈動方面取得了良好的效果。Mucchi和Dalpiaz提出通過比較實驗結果與仿真結果來研究齒輪泵的振動特性,其中對原有模型的進、出口控制體進行修正,得到了齒輪泵進、出口壓力的脈動。隨后,Mucchi等在考慮齒輪泵進口、出口壓力脈動的基礎上,建立了嚙合區域非牛頓流體的湍流模型,得到了更加精確的壓力脈動模型。Tian設計了一個與密閉死腔容積相連的減壓室來吸收壓力脈動,以代替傳統的卸荷槽,表明減壓室能夠衰減95%的壓力脈動峰值。Rituraj等研究了齒輪泵加工制造過程中錐度和同心度對齒輪泵容積效率和出口流量脈動的影響。Mhana和Popov研究表明非對稱齒輪泵的壓力脈動變化相比對稱齒輪泵更加平穩,壓力突變最大發生在進油口第1個密閉齒腔。Frosina等用PumpLinx建立了齒輪泵的三維流體動力學模型,考慮了所有的泄漏。仿真和實驗在壓力脈動幅值和周期上都得到了較好的一致性,同時表明出口壓力越大,壓力脈動幅值越大。Rituraj等針對齒輪泵葉尖泄漏提出了一種適合大范圍工況的快速集中參數方法,模型中考慮了進口壓降和湍流影響,通過HYGESim軟件仿真得到壓力脈動的變化。Mancò和Nervegna提出一種新型的測量技術,通過安裝在驅動齒輪上的壓力傳感器來檢測外部齒輪泵齒間壓力隨時間的變化。實驗中首次證實了在進口側嚙合葉片內壓力峰值的出現,在進口側齒輪脫離時齒腔內存在空化現象。Cinar等采用實驗驗證與理論分析相結合的方法研究齒輪泵密閉腔中壓力大小的分布,從泵的進口到出口分別在殼體等間隔布置了4個傳感器來測量每個腔中壓力的變化,比較精確地預測了齒輪泵轉動過程中壓力的變化情況。

流體的脈動流動主要分為2種類型：① 流道幾何形狀呈周期性變化；② 流體的速度或流動方向呈周期性變化。齒輪泵出口脈動的產生既有出口控制體形狀的周期性變化,又有流體速度方向的周期性變化。旋轉過程中輪齒對出口流場產生擾動,最終形成湍流流動。本文第1節給出了齒輪泵產生壓力脈動的機理,轉頻、齒頻及齒頻的倍頻分量是壓力脈動主要組成部分；第2節采用譜方法給出了齒輪泵出口測點處壓力脈動的表達式,研究了齒輪泵轉頻對齒頻及倍頻的調制作用；第3節分析了齒輪泵壓力脈動的影響因素及工程應用展望；第4節給出結論。

1 齒輪泵壓力脈動模型

采用歐拉法建立齒輪泵每轉過一個齒時產生的壓力脈動方程,首先選擇控制體,如圖1所示將齒輪泵流體域分成4類控制體,分別是等體積控制體Ⅰ(即由輪齒、軸承座、殼體組成)、進口控制體Ⅱ、出口控制體Ⅲ和密閉死腔控制體Ⅳ,齒輪旋轉過程中控制體個數是周期性變化的。根據連續性方程,假設液體在控制體中的流動是穩態流動、且絕熱等熵,得到每個控制體中的壓力與轉角的關系為

(1)

式中：為油液的體積模量；為控制體體積；為齒輪轉動角速度；Δ為控制體中油液流量的變化量。

圖1 齒輪泵流體域中不同的控制體Fig.1 Fluid domain in gear pump segregated into different control volumes

1.1 控制體中的連續方程

1.1.1 等體積控制體

規定控制體中流量的變化量為流入和流出控制體的流量之差,流量在控制體中的傳遞如圖2所示。

Δ=-

(2)

式中：為流入控制體的流量；為流出控制體的流量。

圖2 第i個密閉齒腔體積流量Fig.2 Volumetric flow rates for isolated tooth space i

齒輪泵齒頂間隙、齒側間隙處液體的流動為平板間的庫埃特-泊肅葉流動。

(3)

(4)

式中：h,為通過齒頂間隙從第個控制體流入到第-1個控制體的流量；f,為通過齒側間隙從第個控制體流入第-1個控制體的流量；為第個控制體的壓力；、分別為第個控制體齒頂間隙和齒側間隙；、分別為齒輪的齒寬和齒高(=1,2分別表示主、從動齒輪)；、分別為齒頂圓半徑和齒高一半處對應的半徑；、分別為齒輪齒頂厚度和齒輪節圓處的厚度；為油液黏度；為齒輪的角速度。

控制體與軸承座孔通過側向間隙相連,為平面泊肅葉流動。

(5)

式中：d,為通過齒側間隙從第個控制體流入軸承座孔的流量；為0.5倍的齒根圓齒距；為齒根圓到軸承座孔的徑向距離；為軸承座孔中油液壓力。

聯立式(1)～式(5)可得等體積控制體的連續方程：

(6)

式中：為第個控制體的體積。

在等體積控制體中壓力可表示為

(),())

(7)

式中：主動齒輪側=1,=1,2,…,;從動齒輪側=2,=1,2,…,;、表示主、從動齒輪等體積控制體最大個數；,為等體積控制體壓力脈動的隱函數表達式；()、()分別表示進口、出口控制體壓力。

1.1.2 進口和出口控制體

齒輪泵進口分別跟液壓油箱、主從動齒輪形成的第1個密閉腔、軸承座孔、雙齒嚙合區形成的密閉死腔、卸荷槽相連；齒輪泵出口分別與工作負載、主從動齒輪形成的最后1個密閉腔、雙齒嚙合區形成的密閉死腔、卸荷槽相連。

齒輪泵進口通過端面間隙分別與密閉死腔(壓力)和軸承座孔相連,液體傳輸近似為平面流動,密閉死腔只存在于雙齒嚙合區；與油箱(壓力)和卸荷槽相連的部分,因形狀和尺寸的變化,液體輸送等效為湍流模型。

(8)

(9)

(10)

(11)

式中：為齒輪泵進口與密閉死腔的體積流量；為密閉死腔與軸承座孔的體積流量；為齒輪泵進口與卸荷槽相連時的體積流量；為齒輪泵進口與油箱的體積流量；為卸荷槽與泵進口連接時的流道截面積；為泵進口與油箱連接的流道截面積；=065為湍流系數；Δ=-,Δ=-,為進口控制體壓力；為油液密度。

聯立式(1)、式(3)～式(5)、式(8)～式(11)可得進口控制體的連續方程：

(12)

式中：為齒輪泵進口控制體體積；、分別為主、從動齒輪第1個控制體通過側隙流入進口的流量；、分別為主、從動齒輪第1個控制體通過徑向間隙流入進口的流量；d1,、d2,分別為主、從動齒輪軸承座流入進口控制體的體積流量；表示密閉死腔控制體流入進口控制體的體積流量。

齒輪泵出口壓力由負載大小決定,流體傳遞過程按湍流處理；齒輪泵出口通過齒側間隙與主、從動齒輪密閉腔和密閉死腔相連,流體傳遞設定為平面流動。

(13)

(14)

=(2π)

(15)

式中：為齒輪泵出口與密閉死腔之間的體積流量；為齒輪泵出口與卸荷槽之間的體積流量；為齒輪泵出口與負載之間的體積流量；為體積容量；為卸荷槽與泵出口連接時的流道截面積；Δ=-,為出口控制體壓力信號的高頻成分。

聯立式(1)、式(3)、式(4)、式(13)～式(15)可得出口控制體的連續方程：

(16)

式中：為齒輪泵出口控制體體積；f1,、f2,分別為主、從動齒輪第、個控制體通過側隙流入進口的流量；h1,、h2,分別為主、從動齒輪第、個控制體通過徑向間隙流向進口的流量。

進、出口控制體體積隨齒輪轉角而變化,與齒輪單雙齒嚙合有關,實驗中齒輪泵進、出口控制體的體積和變化率如圖3所示,齒輪泵有12個齒,以30°為一個周期進行變化,其中體積的突變點表示有齒腔突然與進出口控制體連通或斷開,進、出口控制體中壓力變化可表示為

(17)

(18)

式中：和分別為進口、出口壓力脈動的隱函數表達式；()、()分別為主、從動齒輪第、個控制體的壓力。

1.1.3 密閉死腔控制體

齒輪泵密閉死腔只在雙齒嚙合時存在,防止密閉死腔產生過高的壓力,在齒輪兩側擋板上開了對稱的卸荷槽；當密閉死腔減小,壓力增高時高壓側的卸荷槽接通,當密閉死腔增大,壓力減小時,低壓側的卸荷槽接通,卸荷槽接通和斷開的時間與齒輪泵本身的結構有關。

聯立式(1)、式(8)～式(10)、式(13)、式(14)可得密閉死腔控制體的連續方程：

(19)

式中：為密閉死腔控制體體積。

密閉死腔控制體體積的變化與兩對齒輪嚙合點的位置有關,實驗中齒輪泵密閉死腔控制體的體積和變化率如圖4所示,表明每30°周期內只有雙齒嚙合段0～10.73°內存在密閉腔,密閉死腔控制體壓力可表示為

(20)

式中：為密閉死腔壓力脈動的隱函數表達式。

圖4 齒輪泵密閉死腔控制體的體積和變化率Fig.4 Volume and rate of change of gear pump trapped control volume

1.2 齒輪泵壓力脈動方程

式(7)給出了任意一個密閉齒腔的壓力隨轉角的變化,將式(7)應用于主動齒輪側的個密封腔和從動齒輪側的個密封腔得到等體積控制體的方程組,再聯合式(17)、式(18)、式(20)得到齒輪泵轉過一個齒時各控制體的壓力脈動微分方程組。

(21)

求解式(21)的初值由實驗確定,齒輪轉過一個齒的時間段內,根據齒輪的具體結構參數確定方程組的個數和每個方程組內方程的個數,往往無法用一個方程組來完整表達一個周期。以2 500 r/min,負載壓力5 MPa為例,得到齒輪泵出口的壓力脈動如圖5所示。由圖可知齒輪泵出口壓力脈動是周期信號,主要頻率為500 Hz(齒頻),記單齒嚙合產生的壓力脈動信號為()。該模型主要揭示了齒輪泵產生壓力脈動的機理,即主要因為齒輪泵周期性運動,導致各控制體體積呈周期性變化,假設各控制體為剛性體,液壓油不可壓縮,則齒輪泵內部流場呈周期性變化,因而出口壓力呈周期性脈動。雖然該模型揭示了壓力脈動信號主要組成分量(轉頻、齒頻及倍頻)之間的線性疊加作用,但是沒考慮分量間的非線性作用(即轉頻對齒頻及倍頻的調制作用),因而,不能全面地展示壓力脈動包含的信息,第2節在第1節的基礎上從湍流結構組成和能量傳遞角度研究轉頻分量對其他分量的調制作用。

2 齒輪泵出口測點處壓力脈動模型

齒輪泵依靠輪齒嚙合產生的體積變化來吸入和排出流體,傳動過程中有雙齒嚙合區域會形成密閉腔,隨著密閉腔體積減小壓力逐漸增大,當壓力大于出口壓力時,密閉腔中的流體通過間隙流向出口管路,伴隨著漩渦流的產生,因而流場由層流轉變為湍流。Antoniak和Stryczek對齒輪泵流場進行可視化研究,設定了2種不同的操作參數進行對比實驗,均發現齒輪泵出口流場有湍流出現,在非標準條件(即較高轉速(1000±10) r/min、進口負壓(-0.05±0.005) MPa、較高溫度(50±2) ℃、出口高壓(3±0.01) MPa)下出現了明顯的空化泡沫和氣泡群,同時加劇了湍流強度。因此,齒輪泵出口流場中不可避免地會出現湍流現象,屬于壁湍流,但是湍流強度受外界操作參數和齒輪泵自身結構的影響,如齒輪泵內部開設對稱的卸荷槽,一定程度上減少了射流的產生,降低了湍流強度。

湍流流動是一種高度非線性的復雜流動,迄今為止,仍然沒有一個可以完整解釋并描述湍流的定義。人們對湍流的“定義”也只是通過對湍流運動的特征進行綜合列舉。其中,湍流的特征主要包括：不規則性、擴散性、耗散性、連續性、間歇性、記憶特性等。因此無論是提出新理論還是建立工程計算模型都需要用實驗加以確證；另一方面,實驗本身能發現湍流的新現象,進而提出新理論和模型。

湍流實驗是人們最先認識湍流的工具。1883年雷諾通過有色流體流動實驗觀察到層流到湍流的整個流動變化過程,這一方法成為最早研究湍流的流動顯示法,該方法能直觀得到流體運動情況,但不能對流體流動進行定量分析。20世紀30年代,熱線風速儀(HWA)應用到湍流測量中,得到流動的脈動速度,進一步發展了湍流理論,為湍流實驗研究提供了有效的手段。20世紀80年代初,粒子圖像測速儀(PIV)通過粒子成像測量流體速度,可以得到流體流動的速度場和溫度場。到20世紀90年代,人們發明了多普勒全場測速技術(DGV),該方法改進了激光多普勒測速儀(LDV)只能單點測量的缺點,可以測量空間的三維速度,適用于測量高速大流場流體流動。簡單的湍流問題通常可以理論分析近似求解,而實際存在的復雜湍流流動主要通過實驗和數值模擬研究。隨著計算機技術的發展,人們通過某些數值方法對湍流進行模擬,取得與實際比較吻合的結果,常用的數值模擬方法有直接數值模擬、大渦模擬、統計平均法和Reynolds平均法等。其中Reynolds平均法是目前使用最為廣泛的湍流數值模擬方法。根據對Reynolds應力作出的假定或處理方式不同,常用的湍流模型有兩大類：Reynolds應力模型和渦黏模型。其中Reynolds應力模型分為Reynolds應力方程模型和代數應力方程模型；渦黏模型分為零方程模型、一方程模型和兩方程模型。工程中使用最為廣泛的是兩方程模型,最基本的兩方程模型是標準-模型,即分別引入關于湍動能和耗散率的方程。本文采用理論分析和實驗驗證來研究齒輪泵出口測點處的壓力脈動。實驗中測量壓力脈動的高頻壓力傳感器安裝在齒輪泵出口的圓管上,如圖6所示。

圖6 高頻壓力傳感器安裝位置Fig.6 Installation location of high frequency pressure sensor

2.1 不可壓縮均勻各向同性湍流的動力學模型

2.1.1 基本方程

齒輪泵出口湍流結構比較復雜,但是向下游運動過程中,由于沒有外界干擾,逐漸演化成各向同性湍流。假設油液是不可壓縮的,則在測量點附近形成不可壓縮的均勻湍流,對于不可壓縮流體的均勻湍流場,它的平均速度是常向量,可以令平均速度為0。均勻湍流的脈動場滿足Navier-Stokes方程。

運動方程：

(22)

連續方程：

(23)

式中：為方向上的速度；為流體密度；為流體的運動黏性系數。

齒輪泵出口測點處的脈動壓力滿足Poisson方程,在無界的均勻湍流場中,Poisson方程的Green函數為1,于是脈動壓強的解析積分表達式為

(24)

式中：(,)為空間處時刻的壓力；、、為3個坐標軸方向的相對位移；、、為壓力作用點在3個坐標軸方向的坐標。

理論上,給定脈動方程速度場的初始條件,根據均勻湍流的基本方程可以解出均勻湍流場的一個樣本流動。然而,湍流場是隨機過程,要獲得湍流的全部信息,必須給出足夠多的獨立初始場,然后進行統計分析。

不可壓縮均勻湍流場中的湍動能和雷諾應力分別為

(25)

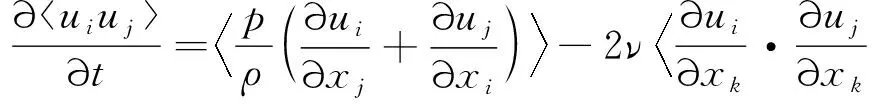
(26)

由式(25)可知,均勻湍流場中湍動能總是衰減的,因此在均勻湍流流動過程中,湍流可能近似的演化為各向同性。

2.1.2 譜分析

均勻湍流是空間上的平穩過程,并且在相關距離很大時,各階相關函數都等于零。這種平穩隨機過程,隨機脈動可以用傅里葉級數展開。根據均勻湍流的譜理論,將均勻湍流在足夠大的三維空間上作傅里葉級數展開,復數形式表示為

(27)

(28)

(29)

(30)

一旦得到湍流脈動的壓力譜在譜空間上的分布,將其代入式(27)就可以得到物理空間的湍流脈動。研究表明“壁湍流”中無論是近壁緩沖區小尺度結構還是對數區的大尺度結構,動力學上均能不相互依賴、自維持地演化,然而實際的湍流場中存在強烈的尺度間的非線性相互作用,特別是當雷諾數升高時,不同區域、不同尺度相干結構之間的相互作用也會增強。Hutchins和Marusic利用湍流邊界層實驗數據,采用傅里葉分解的方法分離出對數區流向尺度大于邊界層厚度的大尺度運動信號,他們發現,這些外區大尺度運動可以深入到近壁區,使得近壁平行于壁面的流向脈動速度分量也包含大尺度的能量,并且這部分來自大尺度的能量隨著雷諾數的升高而增大,而小尺度的速度脈動能量幾乎不變。這一效應也被稱為外區大尺度運動對近壁湍流的疊加效應。同時,Mathis等發現在外區大尺度低速條帶對應區域內,近壁小尺度速度脈動較弱,而在大尺度高速條帶對應區域,近壁小尺度速度脈動較強,這一效應被稱為幅值調制效應。因此,湍流的各尺度分量之間存在線性疊加和非線性的調制作用。

實驗中齒輪泵出口高頻壓力傳感器是基于壓電效應的點測量,得到的脈動信號是一維標量,因此采用周期信號來代替這種平穩隨機信號。齒輪泵旋轉過程中相對于齒輪的嚙合頻率,齒輪的轉頻則要低得多。由于質量偏心、安裝不對中、軸彎曲等原因將導致出現轉頻的低次諧波,如轉頻的1倍頻、2倍頻、3倍頻等,因此轉頻產生的壓力脈動信號傅里葉展開式為

=1,2,…,6

(31)

式中：為直流分量；cos(+)為轉頻的基波分量,為轉頻,為相位角；≥2時,Lcos(+)為轉頻的諧波分量,為相位角。

由于齒輪泵齒腔壓力從進油口到出油口依次增大,主、從動齒輪都會向進油口方向偏斜,這使得轉頻產生的低次諧波分量非常微弱,可忽略,因此式(31)可近似寫為

()=+cos(+)

(32)

式中：、為傅里葉系數。

齒輪泵中每對齒輪的嚙合為一個小周期(即齒頻),而在齒輪泵轉一周過程中有12對齒輪交替進行嚙合形成一個大周期(即轉頻),在一個嚙合周期內,嚙合的齒輪發生了進入嚙合、脫離嚙合、單雙齒嚙合等多次剛度和控制體體積突變的過程,因此在齒輪泵的壓力脈動信號中必然還包含了齒頻的高次諧波成分。齒輪泵轉動過程中,齒輪泵的負載和轉速變化會引起頻譜的諧波分量的調制,負載的變化會引起壓力脈動信號的幅值調制,而轉速的變化會引起相位調制,幅值和相位調制同時進行。調制導致與齒頻相關的邊頻分量增加,因此,在以齒頻為載波頻率的兩側包含了以2個轉頻為調制頻率的邊頻帶。

假設轉頻引起的幅值調制信號為

′()=′cos()

(33)

轉頻引起的相位調制信號為

″()=″sin()

(34)

式中：′為調幅信號幅值；″為調頻信號幅值。

聯立式(21)、式(33)、式(34)得到的脈動信號()的傅里葉展開可表示為

=1,2,…,6

(35)

式中：為常量；H為齒頻產生壓力脈動信號幅值；a為調幅系數；f為調頻系數；為相位角；為齒頻。

聯立式(31)和式(35)可得到齒輪泵出口測點處的壓力脈動傅里葉展開式：

(36)

2.2 實驗驗證

2.2.1 實驗介紹

通過比較完整的轉頻周期內齒輪泵出口壓力脈動的仿真數據和實驗數據來檢驗模型的正確性,齒輪泵的參數如表1所示。

表1 齒輪泵參數Table 1 Parameters of gear pump

根據國家標準(JB/T7041—2006)要求的閉式實驗回路搭建液壓齒輪泵出口壓力脈動測試實驗臺。實驗中分別測試了轉速為2 466.6 r/min、工作負載為10 MPa,轉速為1 453.2 r/min、工作負載為15 MPa,轉速為773.4 r/min、工作負載為10 MPa這3種工況下齒輪泵出口測點處壓力脈動信號,數據采集時的采樣頻率分別為10 240、10 240、5 120 Hz。分別得到不同工況下的時域圖和頻域圖,如圖7所示。從圖7(a)、圖7(c)、圖7(e) 時域圖中看到考慮了轉頻的脈動模型(改進模型)與實驗數據的吻合度更高,而沒有考慮轉頻的脈動模型(原來模型)與實驗數據的誤差較大,尤其在轉速較低時更加明顯,實驗表明轉速對壓力脈動信號影響較大,隨著轉速提高,壓力脈動信號變化趨勢更加平緩,形狀更加接近于標準的正弦信號。從圖7(b)、圖7(d)、圖7(f)頻域圖中可以看到壓力脈動的主要頻率由齒輪泵的轉頻、輪齒嚙合產生的齒頻及齒頻的倍頻組成,轉頻對齒頻及齒頻的倍頻存在明顯的調制作用,證明了壓力脈動信號存在不同尺度信號的線性疊加和非線性的調制,并且轉頻分量隨著轉速的提高而減小,齒頻分量隨轉速提高而增加。因此,式(36)中由齒輪泵轉頻引起的基波分量傅里葉系數、和頻率如表2所示。

表2 不同工況下基波分量的傅里葉系數和頻率

2.2.2 結果分析

從圖7(a)、圖7(c)、圖7(e)可知改進模型仿真結果和實驗數據在變化趨勢上有較好的一致性,說明在研究齒輪泵壓力脈動時,采用周期信號代替平穩隨機信號具有一定的合理性,但也存在一些誤差。誤差的主要來源有：① 齒頂間隙由齒輪偏心位置和泵殼磨損兩部分組成,建模中假設齒輪靜止在靜平衡位置,考慮轉頻的影響本質上是對齒輪實際中心的修正,但跟真實的回轉中心還存在誤差,齒頂磨損是依據經驗估計的,與實際有偏差；② 端面間隙也是根據設計參數和經驗估計的,與齒輪泵真實運行有偏差；③ 齒輪泵出口到高頻壓力傳感器測量點之間并不是等直徑圓管,管路有變徑,造成能量損失,對壓力脈動的幅值產生影響；④ 采用周期信號近似代替平穩隨機信號進行處理,二者存在一定誤差；⑤ 忽略了轉頻產生的壓力脈動信號低次諧波的影響,也會產生一定的誤差。

3 壓力脈動的影響因素分析及工程應用展望

3.1 轉速對壓力脈動的影響

實驗中比較了轉速分別為600、800、1 000、1 500、2 000、2 500 r/min,工作負載為5 MPa這6種工況(實際轉速有波動)下壓力脈動的變化趨勢,并定義峰值指標和脈沖指標分別如式(37)和式(38)所示。如表3所示,通過峰值指標和脈沖指標可以看出:隨著轉速增大,壓力脈動更加平緩,即大周期壓力脈動函數的幅值隨著轉速增大而減小,主要因為轉速越高,相鄰輪齒嚙合的時間越短,流體流動的連續性更好,傳遞時相互之間的壓差變化更小。

峰值指標

(37)

脈沖指標

(38)

表3 不同轉速下壓力脈動指標

3.2 工作負載對壓力脈動的影響

實驗中比較了工作負載分別為5、10、15 MPa,轉速分別為1 500、2 000、2 500 r/min幾種工況(實際轉速有波動)下壓力脈動的變化趨勢,結果如表4所示。可見隨著工作負載增大壓力脈動的幅值增大,即單齒嚙合壓力脈動幅值和大周期壓力脈動的幅值隨著工作負載增大而增大,并且工作負載對壓力脈動的影響要大于速度對壓力脈動的影響。主要因為工作負載越高,流體元受到的剪切力越大,由于流體的易變性,流體質點的相對運動增大,流體流動的連續性減弱,傳遞時相互之間的壓差變化增大。

表4 不同工作負載下壓力脈動指標Table 4 Pressure pulsation index at different workloads

3.3 工程應用展望

在外嚙合齒輪泵的實際使用過程中,齒輪泵出現致命失效、完全失效等失效形式的幾率較小,最常見的失效形式為退化失效,具體表現為輸出流量或壓力不足。造成這種失效形式的主要原因是齒輪泵在運行過程中內部摩擦副不停接觸磨損導致的。磨損失效主要有3種形式,分別為端面磨損、齒面磨損和齒頂磨損,其中端面磨損導致的泄漏占總泄漏量的80%左右,是影響泄漏的最主要因素。行業標準規定實際使用中容積效率低于85%為失效,但是流量的測量存在測量誤差大、準確率低、信號變化不明顯等問題。因此,研究壓力脈動信號與齒輪泵故障之間的內在關系具有重要的意義。

齒輪泵中流量的傳遞如圖8所示,假設在端面磨損前后輸入的流量恒定,且不考慮外泄漏,則輸出流量分成兩部分：一部分由泵的出口管路輸出用于執行機構做功,即,另一部分由泵的內泄漏做無用功,即Δ。泄漏量與間隙之間的關系為

(39)

式中：Δ為間隙兩端壓差；為液壓油動力黏度；為間隙長度；為間隙寬度。

齒輪泵出口管路為圓管,則輸出流量與流速之間的關系為

=·

(40)

式中：為平均流速；為管路截面積。

圖8 齒輪泵的流量輸運Fig.8 Flow transport of gear pump

由式(39)可知,間隙增大,齒輪泵泄漏量增大,則齒輪泵出口流量減小。磨損前后齒輪泵出口管路直徑大小不變,由式(40)可知平均流速減小。平均流速與脈動速度′之間的關系為

(41)

式中：為雷諾數。

由式(41)可知,主流速度減小,則脈動速度′也相應減小,脈動的速度場發生變化,式(24) 表明,一點的脈動壓力是該點領域中脈動速度場的泛函,脈動速度場的變化會導致脈動壓力的變化。因此,壓力脈動信號作為齒輪泵磨損故障的特征信號具有一定的合理性。

齒輪泵通過出口控制體體積變化實現流體的排出,因此出口壓力脈動是齒輪泵的固有特性。從優化齒輪泵壓力脈動減少故障的角度分析,提出以下幾點工程建議：① 在設計齒輪泵時要將固有頻率和壓力脈動頻率錯開,以免發生共振；② 合 理設計齒輪泵浮動軸套背面的密封圈形狀及安裝位置,盡量減少浮動軸套的偏斜,保證合理的端面間隙；③ 改變主、從動齒輪的齒數、外形尺寸來減少出口流量脈動,從而達到減少壓力脈動的目的。

4 結 論

1) 齒輪泵出口流體的流動近似為不可壓縮的均質湍流流動,壓力脈動的頻率主要由齒輪泵的轉頻、齒頻和齒頻的倍頻組成,轉頻對齒頻和齒頻的倍頻產生調制,并且既有調幅調制又有調頻調制。

2) 齒輪泵壓力脈動受轉速和工作負載的影響,隨著轉速提高,壓力脈動減小,隨著工作負載增大,壓力脈動增大,且工作負載對壓力脈動的影響大于轉速對壓力脈動的影響。