基于強化學習的再入飛行器“新質”走廊在線生成技術

惠俊鵬,汪韌,俞啟東

中國運載火箭技術研究院 研究發展部,北京 100076

高升阻比飛行器具有飛行速度快、升阻比高、航程遠、機動能力強等特點,在軍事和民用領域發揮著重要的作用。高升阻比飛行器再入制導技術通過設計制導律,在動力學方程、過程約束、控制量約束等條件下,使得飛行器在中末交班點滿足再入終端約束。因臨近空間環境的復雜性和不確定性,飛行器再入制導技術已成為航空航天領域研究的熱點之一。

高升阻比飛行器再入制導方法主要分為兩種：基于標稱軌跡的制導方法和預測校正制導。基于標稱軌跡的制導方法離線設計標稱軌跡,在飛行過程中跟蹤標稱軌跡進行制導。離線設計的標稱軌跡可以是阻力加速度-能量(Drag-Energy, D-E)剖面、高度-速度(Height-Velocity, H-V)剖面等。由于標稱軌跡是離線設計所得,因而該方法對復雜環境的適應性和魯棒性方面存在明顯的不足。預測校正制導方法對動力學方程進行積分,預測飛行器的終端狀態,并基于終端狀態與目標點的偏差來校正制導指令,從而實現對飛行器的精確制導。相比于基于標稱軌跡跟蹤的制導方法,預測校正制導具有更強的自主性和對復雜環境的適應能力。

人工智能(Artificial Intelligence)目前已成為學術界和工業界的研究熱點。機器學習(Machine Learning)技術是人工智能領域的核心技術,機器學習主要包括監督學習(Supervised Learning)、無監督學習(Unsupervised Learning)和強化學習(Reinforcement Learning)。相比于監督學習和無監督學習,強化學習主要用于解決智能體的序貫決策問題,其核心思想是智能體自主地與環境進行交互,實時觀測狀態信息,并基于一定的策略采取相應的動作,同時從環境中獲取與動作相對應的反饋信息,智能體基于數據[,,]進行訓練,在不斷“試錯”的過程中優化行動策略,以期完成預定任務。近年來提出的具有代表性的強化學習算法有深度Q網絡算法(Deep Q Network, DQN)、深度確定性策略梯度算法(Deep Deterministic Policy Gradient, DDPG)、近端策略優化算法(Proximal Policy Optimization, PPO)、軟動作-評價算法(Soft Actor-Critic, SAC)等,目前已廣泛應用于游戲、無人駕駛等領域。

基于人工智能的飛行器制導控制技術研究尚處于起步階段。文獻[9]綜述了深度學習在飛行器動力學與控制中的應用,從3個方面總結了深度學習在飛行器動力學與控制中的應用,包括：在動力學建模中應用深度學習來提升模型計算效率和建模精度、求解模型反問題；在最優控制中應用深度學習來提升軌跡規劃速度、最優控制實時性和自主性；在飛行器任務設計中應用深度學習來提升任務優化的計算效率和決策水平。在制導律設計方面,文獻[10-12]將深度學習技術應用于飛行器制導和在線軌跡優化問題,基于大量的飛行軌跡訓練神經網絡模型,從而實現飛行器實時狀態到制導指令的快速映射；文獻[13-18]研究了基于Q-Learning、PPO等強化學習算法的智能制導律,該方法消除了原有傳統制導律對飛行器附加的一些不必要約束,通過飛行器與環境的大量交互和試錯,并基于獎勵信息來學習制導律,使得飛行器初步具備了自主決策能力。在姿態控制方面,文獻[19-20]在傳統PID控制的基礎上,進一步利用強化學習技術實現對飛行器6自由度的穩定控制,并驗證了該方法在控制精度和實時性方面的優勢。在飛行器協同制導與軌跡規劃方面,方科等開展了高升阻比飛行器時間協同再入制導研究,將協同再入制導結構分為兩層,其中底層提出了基于神經網絡的時間可控再入制導律,以實現再入飛行時間的可知性與可控性為目標；上層根據不同再入階段特點設計相應的協調函數,生成時間協調信息。周宏宇等提出了一種改進粒子群優化(Particle Swarm Optimization, PSO)算法的飛行器協同軌跡規劃,并借助強化學習方法構建協同需求與慣性權重間的動態映射網絡,提高在線軌跡規劃效率。

無論是基于標稱軌跡的制導還是預測校正制導,都需要基于人工經驗設計飛行走廊參數。基于標稱軌跡的制導方法根據飛行器再入過程中需要滿足的過程約束,設計可行的飛行走廊,在走廊約束下精心設計滿足航程和終端約束的標稱飛行軌跡；預測校正制導方法在橫向制導中通過設置合適的橫程誤差或航向角誤差走廊來確定傾側角的符號,當橫向控制量到達走廊邊界時,傾側角符號翻轉。

本文旨在研究基于強化學習的再入飛行器“新質”走廊在線生成技術,打破傳統預測校正制導等方法中固有的走廊約束,在滿足飛行過程約束(熱流率、過載、動壓等約束)和中末交班點約束的前提下,通過飛行器與環境大量交互“試錯”,并借鑒人類基于反饋來調整學習策略的思想,設置有效的獎勵(反饋)引導,利用強化學習中PPO算法訓練飛行器傾側角制導模型,顛覆現有制導方法在橫向走廊/縱向剖面的約束,實現飛行器基于實時的狀態信息在線決策傾側角指令。通過智能技術的賦能,充分發揮再入飛行器的寬域飛行優勢,進一步拓展飛行剖面,探索已有飛行模式以外的新質飛行走廊,達到出敵不意的靈活飛行效果,從而滿足未來飛行器對智能決策的自主性需求。

1 再入飛行器制導問題

1.1 再入飛行器運動模型

再入飛行器3自由度動力學方程為

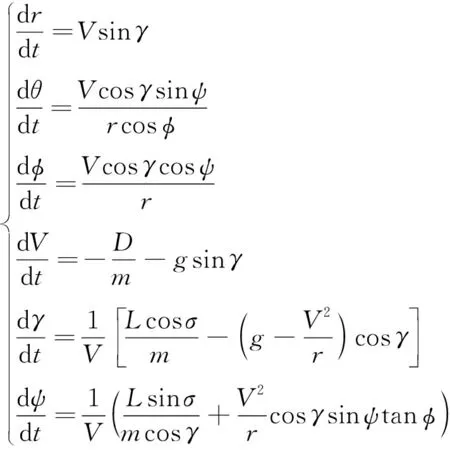
(1)

式中：為地心距；和分別表示飛行器的經緯度；為飛行速度；和分別表示飛行器的航跡角和航向角；表示傾側角；為飛行器的質量；為重力加速度；和分別表示飛行器的升力和阻力。

1.2 再入制導約束

為了保證再入飛行器成功地完成飛行任務,飛行器需滿足各種約束條件,其中核心的約束條件包括過程約束、擬平衡滑翔約束、再入終端約束和控制量約束。

1) 過程約束

一方面,飛行器再入過程中高超聲速氣流會產生嚴重的氣動熱,尤其是飛行器的駐點區域。為保證飛行器各個部件正常運行,再入段制導必須考慮駐點區的熱流率約束。另一方面,飛行器機身和機翼結構強度的上限以及氣動舵面鉸支鏈的承受能力,決定了再入飛行過程中的最大允許過載和動壓。熱流率約束、過載約束和動壓約束是飛行器再入飛行過程中必須要滿足的“硬約束”條件，其表達式為

(2)

2) 擬平衡滑翔約束

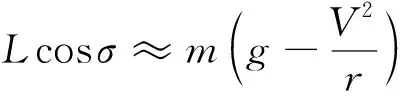
(3)

當滿足擬平衡滑翔條件時,飛行器所受重力與升力的合力恰好與其所受的向心力平衡,此時飛行軌跡高度變化較小,航跡角保持很小的量。

3) 再入終端約束

滑翔段的終端約束為滑翔段和末制導段的交班參數,再入終端約束一般包括高度、速度、經緯度等約束,可表示為

()=,()=,()=,()=

(4)

式中：、、、、分別表示滑翔段的終端時刻、地心距、速度、經度、緯度。

4) 控制量約束

在3自由度飛行器再入制導中,攻角和傾側角為控制量,由于飛行器內部控制機構的作用,控制量的變化需要一定的變化時間和變化速度,不能瞬間變化到指定值。由于攻角采用標準攻角剖面,因而控制量的約束主要限制在傾側角的幅值及其變化率上,即

(5)

2 再入飛行器智能制導模型的設計

在再入飛行器制導中,控制量包括攻角和傾側角。攻角一般通過預先設定的速度-攻角剖面生成。在再入初期為滿足熱流率約束采用大攻角飛行,在中后段為滿足飛行器的射程需求,采用最大升阻比對應的攻角飛行。本文著重研究再入飛行器傾側角制導模型的設計。

2.1 解決的問題

傳統的飛行器再入制導,主要分為2種方法：① 基于標稱軌跡的制導方法,根據飛行器再入過程中需要滿足的熱流率約束、過載約束和動壓約束,設計可行的飛行走廊,飛行走廊一般在D-E剖面或H-V等剖面內描述,在走廊約束下精心設計滿足航程和終端約束的標稱飛行軌跡,實際飛行中在線跟蹤標稱軌跡；② 預測校正制導方法,在縱向制導中基于預測的待飛航程與剩余航程的差,采用割線法迭代求解傾側角的幅值,在橫向制導中通過設置合適的橫程誤差或航向角誤差走廊來確定傾側角的符號,當橫向控制量到達走廊邊界時,傾側角符號翻轉。上述分析表明,無論是基于標稱軌跡的制導還是預測校正制導,都需要基于人工經驗設計飛行走廊參數。

借鑒Alpha Go的思想,將監督學習方法和強化學習方法相結合應用于飛行器再入制導中,研究框架如圖1所示,主要包括3步：

1) 預測校正制導：基于預測校正制導方法,通過靈活設置飛行器再入初始點的狀態參數,生成大量的樣本數據。

2) 監督學習：建立傾側角智能制導模型,利用監督學習中帶有動量的隨機梯度下降(Stochastic Gradient Descent with Momentum,SGDM)算法和第1步產生的樣本數據,訓練傾側角智能制導模型,這里記基于SGDM算法訓練得到的傾側角智能制導模型的參數為。

3) 強化學習：以第2步訓練得到的智能制導模型參數為初始化參數,進一步利用強化學習在智能決策方面的優勢,在動力學方程的約束下通過飛行器與環境進行大量交互,并借鑒人類基于反饋來調整學習策略的思想,設置有效的獎勵(反饋),利用強化學習中PPO算法進一步訓練飛行器傾側角制導模型,得到PPO算法再訓練后的模型參數,記為。該制導模型和參數將顛覆現有制導方法在橫向走廊的約束,在滿足飛行器過程約束的前提下,進一步拓展飛行剖面,生成完全不同于傳統制導方法的飛行走廊,達到出敵不意的靈活飛行效果,從而滿足未來飛行器對智能決策的自主性和實時性要求。

圖1 再入飛行器智能制導研究框架Fig.1 Research framework of intelligent guidance of reentry vehicles

將監督學習方法與強化學習方法相結合應用于再入制導具有2個方面的優勢：

1) 相比于監督學習方法,監督學習是利用神經網絡模型對再入飛行器制導指令的解算過程進行擬合,其本質上是使得基于監督學習訓練的智能制導模型生成的飛行軌跡最大程度逼近預測校正制導方法下的飛行軌跡。因而,可以利用監督學習對傾側角智能制導模型進行預訓練,利用領域知識(預測校正制導方法)引導制導模型中未知參數的搜索。

2) 相比于強化學習方法,若沒有監督學習的預訓練過程,直接利用強化學習算法訓練傾側角智能制導模型將帶來訓練難以收斂等問題。強化學習訓練過程是以監督學習預訓練出的模型參數為初始化參數,進一步通過飛行器與環境的大量交互,通過獎勵的引導,探索完全不同于傳統方法的“新質”飛行走廊。

2.2 傾側角智能制導模型

傾側角智能制導模型如圖2所示,其中制導模型的輸入為飛行器的狀態向量,定義狀態向量為

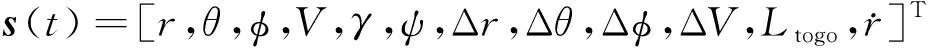
(6)

式中：Δ=-表示時刻的地心距與滑翔終端地心距的差；Δ=-表示時刻的經度與滑翔終端經度的差；Δ=-表示時刻的緯度與滑翔終端緯度的差；Δ=-表示時刻的速度與滑翔終端速度的差;表示時刻飛行器距離滑翔終端的剩余航程：

=×arccos[sinsin+coscos·

cos(-)]

(7)

其中：為地球半徑。隱層為長短期記憶(Long Short-Term Memory, LSTM)模型,隱層輸出的節點數為64個,隱層到輸出層是全連接,輸出為傾側角。

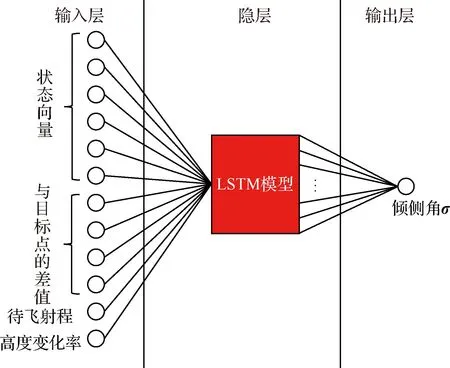
圖2 基于LSTM的傾側角制導模型架構Fig.2 Structure diagram of bank angle guidance model based on LSTM neural network

LSTM模型如圖3所示,其數學表達式為

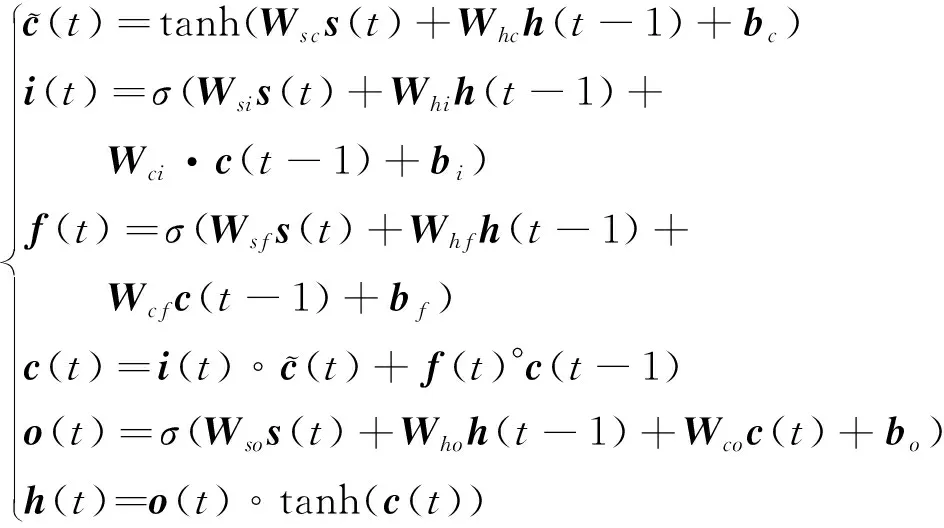
(8)

圖3 LSTM模型Fig.3 LSTM model

選取LSTM模型的根本原因在于,從智能決策的角度來說,飛行器傾側角的決策屬于典型的序貫決策問題,每一時刻的傾側角符號不僅取決于飛行器當前時刻的狀態,還與上一時刻的傾側角符號以及上一時刻航向角誤差與走廊的關系有關。這是因為若上一時刻航向角誤差在走廊內,當前時刻超出走廊,則需要翻轉；但若上一時刻已經超出走廊,傾側角已經翻轉過一次,當前時刻還在走廊外,則無需二次翻轉。因而在決策傾側角時需要考慮飛行器在相鄰時刻間的狀態關系,而這也恰好是LSTM所具有的獨特優勢,是解決序貫決策的經典模型。

2.3 傾側角幅值的約束

為保證再入飛行器的安全飛行,基于LSTM模型輸出的傾側角需進一步滿足再入過程約束。飛行器的指數大氣密度、升力和阻力的計算公式為

(9)

將式(9)代入式(2)的約束條件得到在H-V剖面再入走廊的邊界:

(10)

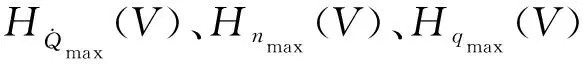
然而,在再入飛行過程中,如果時刻判斷高度-速度剖面是否滿足過程約束的邊界條件會帶來較大的計算量,為此將上述再入過程約束式(10) 轉化為對傾側角幅值的約束：

(11)

|()|}

(12)

基于式(12)對基于LSTM模型輸出的傾側角幅值進一步限制,使其滿足過程硬約束條件。

3 基于監督學習的再入飛行器傾側角智能制導模型的訓練

基于監督學習的再入飛行器傾側角智能制導模型的訓練分為兩步：一是訓練樣本的生成;二是傾側角制導模型的訓練。

3.1 訓練樣本的生成

在訓練樣本的生成方面,本文選取美國通用航空飛行器CAV-H為研究對象,基于預測校正制導方法產生仿真數據。參數設置為

2) 中末交班點參數：高度=23 km,經度為=50°,緯度為=3°,速度為=1 100 m/s。

3) 攻角剖面：

=

(13)

式中：、分別為初始、末端速度；、為可調的速度參數,本文設置=5 000 m/s,=2 500 m/s;為最大攻角,本文設置為20°;max為最大升阻比對應的攻角,本文設置為10°。

4) 縱向預測校正的周期：當剩余射程大于500 km時,=50 s；當剩余射程小于500 km,大于200 km時,=15 s；當剩余射程小于200 km時,=5 s。

5) 動力學方程積分步長：縱向制導的積分步長為1 s,橫向制導的積分步長為0.1 s。

6) 飛行器再入初始點的狀態參數設置如表1所示。

表1 飛行器再入初始點的參數范圍Table 1 Range of initial state parameters of vehicle reentry

在上述參數范圍內隨機設置飛行器的再入初始點參數,在預測校正制導下可以獲得大量的飛行軌跡數據。本文選取其中1 331條飛行軌跡,每條軌跡約16 000個樣本點。

3.2 傾側角智能制導模型的訓練

將基于預測校正制導方法生成的1 331條飛行軌跡輸入圖2基于LSTM的飛行器傾側角制導模型中,基于監督學習的思想,在訓練時目標損失函數(Loss function)定義為

(14)

(15)

訓練效果如圖4和圖5所示。可以看出目標損失函數和均方誤差隨著訓練迭代次數的增加逐漸減小且趨于收斂,表明上述訓練參數設置的合理性。

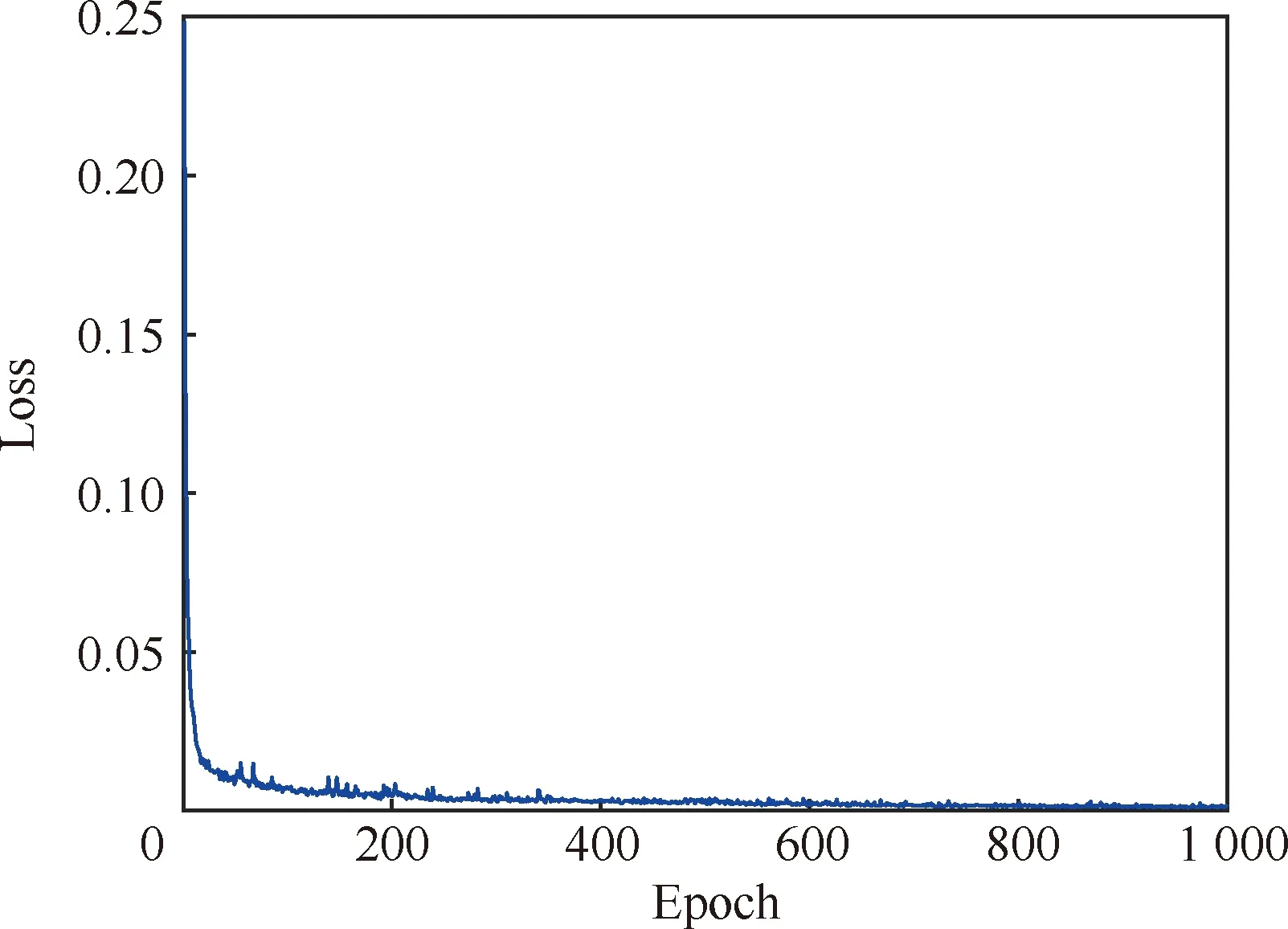
圖4 損失函數隨迭代次數的變化曲線Fig.4 Loss function vs epoch curve

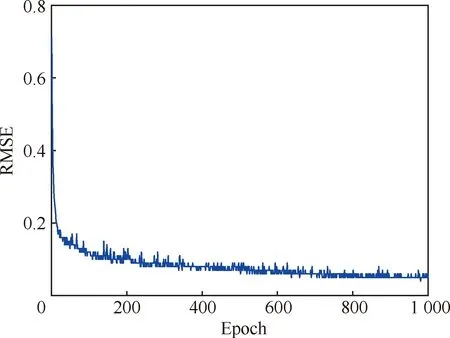
圖5 均方根誤差隨迭代次數的變化曲線Fig.5 RMSE vs epoch curve

4 基于強化學習的再入飛行器傾側角制導模型的訓練

記第3節中基于監督學習SGDM算法訓練得到的傾側角智能制導模型的參數為,本節將以參數為初始化參數,進一步利用強化學習的思想,將強化學習技術應用于飛行器再入制導中,在動力學方程的約束下通過飛行器與環境進行大量交互,在“試錯”的過程中根據設置的有效獎勵(反饋),利用PPO強化學習算法訓練飛行器傾側角制導模型,得到PPO算法訓練后的模型參數,記為進一步拓展飛行剖面,生成完全不同于傳統制導方法的飛行走廊,包括再入飛行器馬爾科夫決策過程建模和PPO算法原理。

4.1 再入飛行器馬爾科夫決策過程建模

基于強化學習研究再入飛行器制導律,需首先利用馬爾科夫決策過程對再入制導問題進行建模,主要包括3部分：飛行器的狀態空間、動作空間和獎勵(反饋)的設計。

飛行器的動作空間為傾側角,包括傾側角的幅值和符號：

=

(16)

獎勵函數在利用強化學習算法訓練傾側角智能制導模型中起著引導的作用,不同的獎勵函數對訓練結果將產生不同影響。若只考慮是否滿足中末交班點的精度要求,即無過程獎勵信息,則稀疏獎勵會帶來訓練難以收斂的問題。結合再入飛行器的飛行特性,傾側角影響橫向制導的經緯度和縱向制導的高度、速度,因而獎勵的設置從橫向和縱向2個維度來設置。

1) 橫向獎勵的設置

橫向獎勵的設置如圖6所示,著重考慮2個方面：① 為了增加飛行器與環境交互過程中的探索性,期望其能夠探索出完全不同于傳統預測校正制導的飛行軌跡,因而在接近目標點一定距離后才設置相應的獎勵,如本文中考慮剩余航程小于1 000 km后才設置獎勵；② 為了引導飛行器精確到達目標點,在飛行器接近目標點的過程中,距離越近,獎勵的設置越密集,飛行器獲得的獎勵越大,且飛行器一旦遠離目標點則被懲罰(負獎勵),該負獎勵將迅速抵消接近目標飛行過程獲得的正獎勵,從而引導飛行器精確到達目標點。

圖6 飛行器橫向獎勵的設置Fig.6 Lateral reward set of reentry vehicles

2) 縱向獎勵的設置

除了滿足中末交班點經緯度約束外,還需滿足高度和速度的約束,從能量的角度出發,定義飛行器的能量為

(17)

式中：表示飛行器的能量；GM表示引力系數,取值為3.986×10N·m/kg。飛行器在位置點(,)所具有的能量均值為,將飛行器獲得的獎勵設置為能量的高斯分布函數：

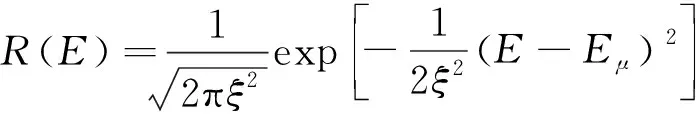
(18)

式中:為標準差。通過如圖7所示的飛行器縱向獎勵的設置,引導飛行器在位置點(,)處的能量在[-,+]的范圍內,以確保飛行器具備足夠的能量到達目標點。

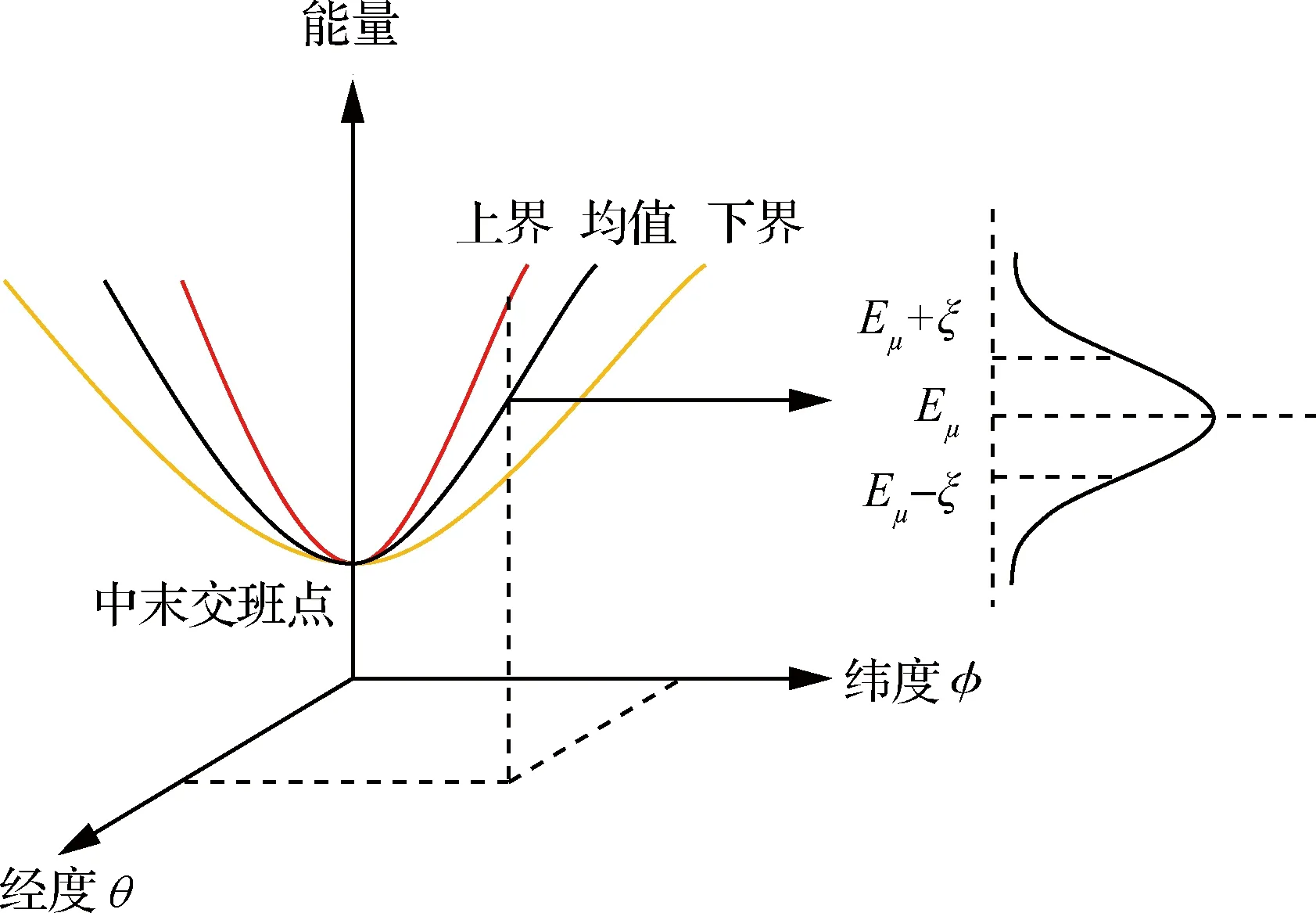
圖7 飛行器縱向獎勵的設置Fig.7 Longitudinal reward set of reentry vehicles

4.2 PPO算法原理

PPO算法在連續動作空間的智能決策任務中表現出較好的效果,目前Open AI已經將PPO作為強化學習研究的首選算法。

1) 優化的目標函數

定義優化的目標函數為

(19)

式中：～()表示飛行器的初始狀態分布；記2.2節中設計的傾側角智能制導模型為(|),它實現的是從飛行器狀態到動作(即傾側角指令)的映射;為傾側角智能制導模型(或策略模型)中待訓練的參數；()為獎勵函數,表示飛行器在狀態執行動作獲得的即刻獎勵的期望；∈[0,1]為折扣因子。

在強化學習算法中,一般采用策略梯度法來更新策略參數從而最大化目標函數。策略參數的更新方程為

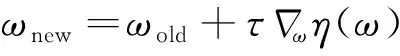
(20)

策略梯度算法的關鍵在于如何選擇更新步長,合適的步長是指當策略更新后,目標函數的值單調增加,或單調不減,這是PPO算法要解決的關鍵問題。

2) PPO算法的核心思想

PPO算法是由信賴域策略優化(Trust Region Policy Optimization, TRPO)算法演變而來。TRPO算法并不是從策略梯度的更新步長著手,而是從優化的目標函數出發。鑒于目標函數難以優化,尋找替代函數(Surrogate Function),替代函數具有3個特點：① 替代函數是目標函數的下界函數；② 在當前策略下替代函數近似等于目標函數；③ 替代函數相比于目標函數更容易優化。

TRPO算法用一個替代函數來作為目標函數的下界函數,下界函數易于優化,通過迭代的方式讓下界函數逼近原目標函數的最優解。在TRPO算法中,將式(19)中的目標函數轉化為

(21)

式中：(|)表示參數更新前的策略；由于(|)表示更新后的策略,是未知的,無法基于未知分布(|)采樣得到動作序列,因而利用重要性采樣(Importance Sampling),即～(|)獲得采樣動作序列；(,)=(,)-()表示優勢函數(Advantage Function),它描述的是動作值函數(,)相比于狀態值函數()的優勢,如果優勢函數大于零,則說明該動作比平均動作好,如果優勢函數小于零,則說明當前動作不如平均動作好。((·|)|(·|))表示分布(·|)與(·|)之間的KL散度(Kullback-Leibler Divergence),引入該約束條件的目的是限制每一步策略參數的更新幅度。

TRPO算法能夠保證在迭代的過程中飛行器的制導策略朝著最優的方向不斷更新,并能確保算法的收斂性,但其計算過程比較復雜。為此,PPO算法將TRPO中KL散度的約束直接體現在目標函數中,移除了KL散度的計算,從而簡化了TRPO算法。

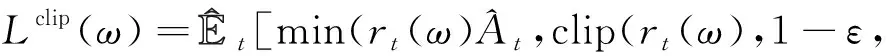
1+)(,))]

(22)

由目標函數可知：

① 當舊策略(|)表現較好時,即優勢函數(,)>0,此時由clip((),1-,1+)(,))可得(|)(|)≤1+,其表達的意思是此時策略表現較好,理應讓(|)變大,但不能使(|)(|)變得過大,導致策略更新前后相差太大,引入的方差較大。

② 當舊策略(|)表現不好時,即優勢函數(,)<0,此時由clip((),1-,1+)(,))可得(|)(|)≥1-,其表達的意思是此時策略表現不好,策略更新的比值(|)(|)不必受到限制。

因而,PPO算法通過clip((),1-,1+),將策略更新的比值(|)(|)約束在[1-,1+]之內。

由上述分析過程可以看出PPO算法避免了復雜的KL散度的計算過程,并將有約束的優化問題轉化為無約束的優化問題,大大簡化了計算復雜度,提升算法收斂性能。

5 仿真與分析

5.1 不同制導方法對比分析

以通用航空飛行器(Common Aero Vehicle-H, CAV-H)為研究對象,參數設置見3.1節,比較3種不同制導方法的仿真結果：① 預測校正制導方法；② 第3節中基于監督學習中SGDM算法訓練傾側角制導模型的方法(圖中記為“LSTM模型+SGDM算法”)；③ 第4節中基于強化學習中PPO算法訓練傾側角制導模型的方法(圖中記為“LSTM模型+PPO算法”),對比結果如圖8～圖12所示。

由圖8～圖12可以看出,“預測校正制導”與“LSTM模型+SGDM算法”兩種制導方式下的飛行軌跡基本重合,這是由于利用監督學習訓練傾側角制導模型時,選取的樣本軌跡是基于預測校正制導產生,該訓練過程可理解為對預測校正制導的擬合過程。但“LSTM模型+PPO算法”制導下的飛行軌跡完全不同于預測校正制導下的飛行軌跡。從圖9經緯度曲線和圖10傾側角曲線可以看出,預測校正制導從初始點(0°,0°)出發,由于航向角=90°且傾側角大于>0°,因而初始飛行軌跡朝東南方向；相反,在“LSTM模型+PPO算法”制導下從初始點(0°,0°)出發后輸出的傾側角<0°,因而初始飛行軌跡朝東北方向。盡管兩種不同的制導方式下飛行軌跡完全不同,但在滿足熱流率約束、過載約束和動壓約束的前提下,都精確到達中末交班點。

圖8 高度-速度曲線對比Fig.8 Comparison of height-velocity curves

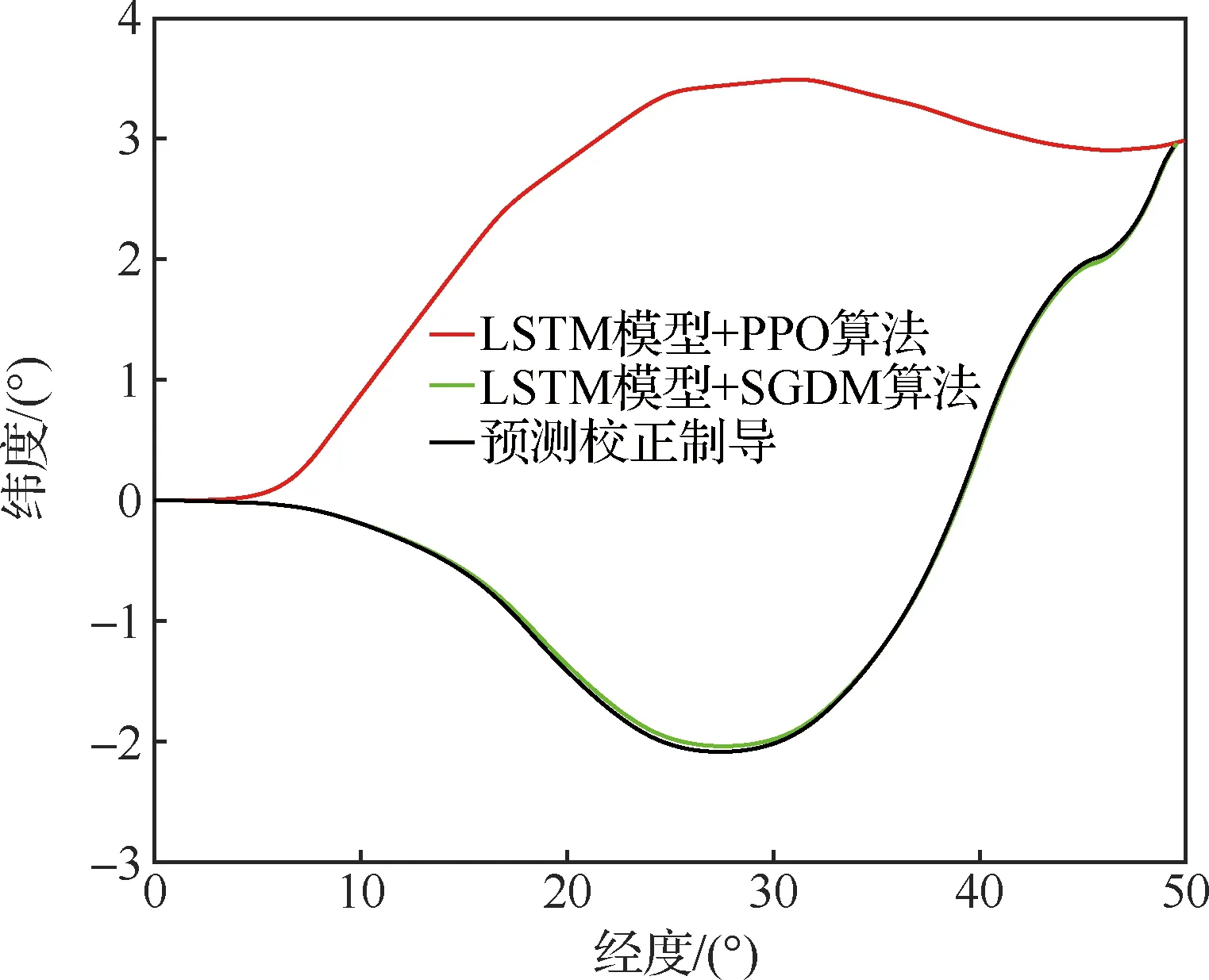
圖9 橫向軌跡曲線對比Fig.9 Comparison of lateral trajectory curves

圖10 傾側角-速度曲線對比Fig.10 Comparison of bank angle-velocity curves

圖11 航跡角-時間曲線對比Fig.11 Comparison of flight path angle-time curves

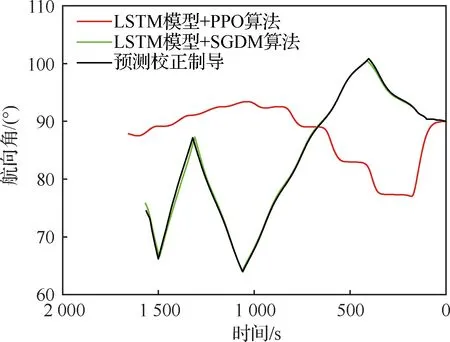
圖12 航向角-時間曲線對比Fig.12 Comparison of heading angle-time curves

5.2 Monte Carlo仿真分析

為驗證“LSTM模型+PPO算法”制導方法的魯棒性和對參數偏差的適應性,本文對飛行器再入初始狀態、氣動參數進行拉偏仿真分析,偏差設置如表2所示。

表2 飛行器再入初始狀態和氣動參數偏差

在再入初始狀態擾動和氣動偏差的條件下,基于“LSTM模型+PPO算法”制導進行400組的Monte Carlo仿真,落點經緯度的散布如圖13所示,并與傳統的預測校正制導進行比較。可以看出,在滿足中末交班點能量約束的前提下,相比于傳統的預測校正制導方法,基于“LSTM模型+PPO算法”制導的末端狀態更加靠近中末交班點,即更加靠近=50°,=3°。顯然,在初始狀態有擾動和氣動參數有偏差的情形下,“LSTM模型+PPO算法”制導具有更高的精度,其原因在于采用LSTM模型輸出傾側角指令時需對輸入的飛行器狀態向量進行歸一化處理,該過程會降低對狀態偏差的敏感性,加上LSTM神經網絡模型具有天然的泛化能力,因而對于參數的偏差具有更強的魯棒性。

圖13 初始狀態和氣動參數擾動下落點經緯度的散布圖Fig.13 Longitude and latitude scatter diagram with initial state error and aerodynamic parameter perturbation

5.3 實時性分析

下面進一步對比分析不同制導方法的實時性。運行硬件為Intel Core(TM) i7-6500U CPU @2.50 GHz,在Matlab環境下運行代碼。

在Monte Carlo仿真中,基于“LSTM模型+PPO算法”制導方法完成一次再入段飛行的平均時長為8.91 s,其具體分布如圖14所示,其中基于LSTM模型生成傾側角的時長占其中的6.24 s,龍格庫塔RK-4積分時長占其中的1.80 s。

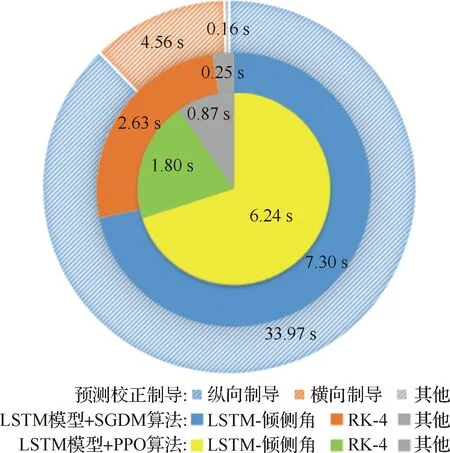
圖14 計算實時性對比分析Fig.14 Comparison of computing time analysis

與之對比,在Monte Carlo仿真中,基于預測校正制導方法完成一次再入段飛行的平均時長為38.69 s,其中縱向制導過程占其中的33.97 s,橫向制導過程占其中的4.56 s。這是因為在縱向制導中,對動力學方程進行積分的預測過程和基于割線法求解傾側角的校正過程計算量較大,占用的時間較長。此外,基于“LSTM模型+SGDM算法”的制導方法與基于“LSTM模型+PPO算法”的制導方法耗時相當,這是由于訓練算法雖然不一樣,但均是基于LSTM模型生成傾側角指令,這兩種制導方法中沒有“預測”環節和“積分”環節,大大減少了計算量,提高了計算速度。因而,在實時性方面,基于LSTM模型的制導方法相比于傳統預測校正制導具有明顯的優勢。

6 結 論

傳統基于標稱軌跡制導和預測校正制導等方法普遍存在人工設置的飛行走廊的固有約束,為打破該約束條件的限制,本文將監督學習技術和強化學習技術應用于飛行器再入制導中：① 基于預測校正制導方法生成大量的飛行軌跡樣本；② 建 立傾側角智能制導模型,利用監督學習中帶有動量的隨機梯度下降算法訓練傾側角智能制導模型；③ 在第2步基于監督學習訓練的傾側角智能制導模型的基礎上,利用強化學習在智能決策方面的優勢,在動力學方程的約束下通過飛行器與環境進行大量交互,并設置有效的獎勵,利用強化學習中PPO算法進一步訓練飛行器傾側角制導模型,顛覆現有制導方法中橫向走廊的約束,進一步拓展飛行剖面,生成完全不同于傳統制導方法的飛行走廊,達到出敵不意的靈活飛行效果。強化學習技術通過飛行器與環境的大量交互“試錯”,優化飛行軌跡,其與制導控制技術的交叉融合是未來飛行器智能制導控制領域的熱門研究方向。