基于材料場級(jí)數(shù)展開的結(jié)構(gòu)動(dòng)力學(xué)拓?fù)鋬?yōu)化

梁寬,付莉莉,張曉鵬,*,羅陽軍

1. 大連理工大學(xué) 工業(yè)裝備結(jié)構(gòu)分析國家重點(diǎn)實(shí)驗(yàn)室, 大連 116024 2. 西安航天動(dòng)力研究所,西安 710100

振動(dòng)在航空航天薄壁結(jié)構(gòu)中十分普遍,然而劇烈的振動(dòng)將導(dǎo)致結(jié)構(gòu)性能下降并帶來安全隱患。通過優(yōu)化技術(shù)對(duì)結(jié)構(gòu)中材料與設(shè)備的合理布局以改善提高振動(dòng)系統(tǒng)的動(dòng)力學(xué)性能具有重要的意義。在各類優(yōu)化方法中,結(jié)構(gòu)動(dòng)力學(xué)拓?fù)鋬?yōu)化被認(rèn)為是改善結(jié)構(gòu)動(dòng)力學(xué)設(shè)計(jì)的最有效途徑,近年來受到學(xué)者的廣泛關(guān)注。目前主流的結(jié)構(gòu)拓?fù)鋬?yōu)化方法,如變密度法、水平集法、漸進(jìn)結(jié)構(gòu)方法等,均已應(yīng)用于結(jié)構(gòu)動(dòng)力學(xué)拓?fù)鋬?yōu)化問題設(shè)計(jì)中。

相比于結(jié)構(gòu)靜力學(xué)拓?fù)鋬?yōu)化問題,結(jié)構(gòu)動(dòng)力學(xué)拓?fù)鋬?yōu)化問題面臨著因局部最優(yōu)解陷阱而導(dǎo)致的收斂困難、靈敏度分析復(fù)雜、局部模態(tài)等諸多難點(diǎn),限制了結(jié)構(gòu)動(dòng)力學(xué)拓?fù)鋬?yōu)化方法的發(fā)展和應(yīng)用。針對(duì)上述困難,部分學(xué)者開展了長期的研究工作。例如,Du和Olhoff提出了廣義增量頻率(GIF)拓?fù)鋬?yōu)化方法,從而克服了動(dòng)力學(xué)優(yōu)化中結(jié)構(gòu)高頻振動(dòng)多峰值帶來的收斂性和局部最優(yōu)解難題。

結(jié)構(gòu)動(dòng)力學(xué)優(yōu)化問題的研究目標(biāo)主要分為3大類,包括：結(jié)構(gòu)固有頻率優(yōu)化、結(jié)構(gòu)穩(wěn)態(tài)響應(yīng)優(yōu)化、結(jié)構(gòu)瞬態(tài)動(dòng)力學(xué)優(yōu)化。經(jīng)過多年的研究,固有頻率的結(jié)構(gòu)優(yōu)化方法獲得了長足的發(fā)展,并在結(jié)構(gòu)重頻率等難題中取得了重要的研究成果。近年來,學(xué)者們更為關(guān)注結(jié)構(gòu)穩(wěn)態(tài)與瞬態(tài)動(dòng)力荷載下結(jié)構(gòu)動(dòng)力學(xué)拓?fù)鋬?yōu)化的研究。在結(jié)構(gòu)穩(wěn)態(tài)動(dòng)力學(xué)拓?fù)鋬?yōu)化研究中,Rong等研究了能夠有效抑制隨機(jī)激勵(lì)下動(dòng)力學(xué)局部模態(tài)的結(jié)構(gòu)拓?fù)鋬?yōu)化方法；Zhu等研究了受到基礎(chǔ)簡諧振動(dòng)的結(jié)構(gòu)動(dòng)力學(xué)拓?fù)鋬?yōu)化方法,鄭玲等則研究了基于漸進(jìn)優(yōu)化算法的車身結(jié)構(gòu)減振降噪阻尼材料最優(yōu)拓?fù)鋬?yōu)化布局方法。在結(jié)構(gòu)瞬態(tài)動(dòng)力學(xué)優(yōu)化中,Zhang和Kang研究了瞬態(tài)動(dòng)力載荷下基于主動(dòng)振動(dòng)的壓電智能結(jié)構(gòu)拓?fù)鋬?yōu)化方法；Yun和Youn研究了瞬態(tài)動(dòng)力載荷下結(jié)構(gòu)黏彈性阻尼材料最優(yōu)拓?fù)洳季址椒ā?/p>

已有研究雖然解決了部分結(jié)構(gòu)穩(wěn)態(tài)與瞬態(tài)動(dòng)力學(xué)優(yōu)化中的難題,但因結(jié)構(gòu)動(dòng)力學(xué)優(yōu)化問題中的靈敏度分析與局部最優(yōu)解陷阱等困難,使得結(jié)構(gòu)動(dòng)力學(xué)響應(yīng)能夠處理的目標(biāo)函數(shù)類型有限,限制了結(jié)構(gòu)動(dòng)力學(xué)拓?fù)鋬?yōu)化問題的應(yīng)用。例如,在穩(wěn)態(tài)工程結(jié)構(gòu)動(dòng)力學(xué)拓?fù)鋬?yōu)化中,往往希望結(jié)構(gòu)的動(dòng)力學(xué)響應(yīng)在整個(gè)工作頻率區(qū)間內(nèi)都具有較小的結(jié)構(gòu)動(dòng)力學(xué)響應(yīng)。基于梯度的結(jié)構(gòu)動(dòng)力學(xué)拓?fù)鋬?yōu)化方法,需要引入頻率區(qū)間積分或者包絡(luò)函數(shù)以實(shí)現(xiàn)目標(biāo)函數(shù)的光滑化,從而可采用基于梯度的結(jié)構(gòu)拓?fù)鋬?yōu)化方法進(jìn)行優(yōu)化問題的求解。然而簡諧激勵(lì)下結(jié)構(gòu)指定位置在不同頻率下振幅變化往往十分劇烈,并具有“多峰值”特性,使得包絡(luò)函數(shù)等呈現(xiàn)病態(tài)特性,導(dǎo)致優(yōu)化效果不理想甚至是不收斂。采用基于非梯度優(yōu)化算法的結(jié)構(gòu)拓?fù)鋬?yōu)化方法進(jìn)行穩(wěn)態(tài)與瞬態(tài)動(dòng)力學(xué)載荷下結(jié)構(gòu)拓?fù)鋬?yōu)化是克服這些困難的可能途徑,目前國內(nèi)外尚未見相關(guān)研究。

最近提出的材料場級(jí)數(shù)展開(Material-Field Series-Expansion,MFSE)方法通過連續(xù)體拓?fù)浔碚骱徒稻S映射能夠大幅度減少拓?fù)鋬?yōu)化問題中設(shè)計(jì)變量個(gè)數(shù),從而能夠有效解決傳統(tǒng)拓?fù)鋬?yōu)化設(shè)計(jì)變量過多的難題,并結(jié)合序列Kriging代理模型算法,能夠高效實(shí)現(xiàn)非梯度拓?fù)鋬?yōu)化問題求解。這一優(yōu)化策略具有不需要梯度信息、適合復(fù)雜非線性問題、具備一定的全局搜索能力、可充分利用并行計(jì)算等優(yōu)勢,十分適合求解復(fù)雜的結(jié)構(gòu)穩(wěn)態(tài)與瞬態(tài)動(dòng)力學(xué)拓?fù)鋬?yōu)化問題。

本文基于文獻(xiàn)[21]中的結(jié)構(gòu)拓?fù)浔碚骱头翘荻韧負(fù)鋬?yōu)化方法,給出了穩(wěn)態(tài)載荷下結(jié)構(gòu)指定頻率區(qū)間內(nèi)響應(yīng)以及瞬態(tài)載荷下指定關(guān)心時(shí)間區(qū)間的結(jié)構(gòu)動(dòng)力學(xué)非梯度拓?fù)鋬?yōu)化列式。采用有限元方法對(duì)結(jié)構(gòu)的穩(wěn)態(tài)與瞬態(tài)動(dòng)力學(xué)響應(yīng)進(jìn)行求解,并基于材料場級(jí)數(shù)展開(MFSE)和序列Kriging代理模型優(yōu)化算法,實(shí)現(xiàn)復(fù)雜動(dòng)力學(xué)響應(yīng)目標(biāo)下結(jié)構(gòu)拓?fù)鋬?yōu)化問題的求解。

1 結(jié)構(gòu)動(dòng)力學(xué)響應(yīng)優(yōu)化問題描述

在外加動(dòng)力載荷作用下,基于有限元離散的結(jié)構(gòu)振動(dòng)方程可以表示為

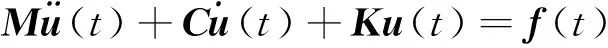
(1)

式中：、和為維矩陣,分別表示結(jié)構(gòu)的總質(zhì)量陣、總阻尼陣和總剛度陣,為結(jié)構(gòu)總自由度個(gè)數(shù);為結(jié)構(gòu)瞬態(tài)位移響應(yīng);()為外加動(dòng)載荷。

若考慮結(jié)構(gòu)承受瞬態(tài)荷載,求解其瞬態(tài)動(dòng)力學(xué)響應(yīng)的一般方法是,將方程(1)在時(shí)間域上進(jìn)行離散,常見的求解方法為Newmark法、Wilson-法等。通過逐步積分,可計(jì)算出任意指定時(shí)刻的結(jié)構(gòu)振動(dòng)響應(yīng)()。

當(dāng)結(jié)構(gòu)受到簡諧激勵(lì)()=ei(表示載荷向量幅值,為外激勵(lì)圓頻率)的作用,其穩(wěn)態(tài)位移響應(yīng)可表示為()=ei(表示結(jié)構(gòu)振幅向量)。因此,結(jié)構(gòu)穩(wěn)態(tài)動(dòng)力學(xué)方程可由式(1)可得到如下：

(-+iθ+)=

(2)

基于上述方程,提出適當(dāng)?shù)哪繕?biāo)函數(shù)和約束函數(shù),選取精確高效的結(jié)構(gòu)拓?fù)涿枋瞿Ｊ?即可建立結(jié)構(gòu)動(dòng)力學(xué)拓?fù)鋬?yōu)化模型。

對(duì)穩(wěn)態(tài)結(jié)構(gòu)動(dòng)力學(xué)響應(yīng)優(yōu)化問題而言,結(jié)構(gòu)動(dòng)力學(xué)拓?fù)鋬?yōu)化常選擇結(jié)構(gòu)動(dòng)柔度為目標(biāo)函數(shù),結(jié)構(gòu)動(dòng)柔度(=||)可以表征結(jié)構(gòu)整體的動(dòng)響應(yīng)特征。為了抑制結(jié)構(gòu)穩(wěn)態(tài)動(dòng)響應(yīng)多峰值而帶來的數(shù)值困難,本文選擇動(dòng)柔度對(duì)數(shù)為目標(biāo)函數(shù),其表達(dá)如下：

(3)

對(duì)結(jié)構(gòu)瞬態(tài)動(dòng)力響應(yīng)優(yōu)化而言,其目標(biāo)函數(shù)往往選取關(guān)心位置在指定時(shí)間段內(nèi)的動(dòng)力學(xué)響應(yīng)的積分作為目標(biāo)函數(shù),考慮到振動(dòng)瞬態(tài)響應(yīng)會(huì)隨時(shí)間產(chǎn)生正負(fù)號(hào)交替,常取振幅響應(yīng)的平方(或絕對(duì)值)在時(shí)間上的積分。因此,本文選取結(jié)構(gòu)指定位置瞬態(tài)的動(dòng)力響應(yīng)為目標(biāo)函數(shù)：

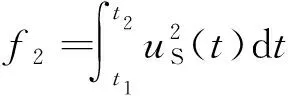
(4)

結(jié)構(gòu)動(dòng)力學(xué)優(yōu)化設(shè)計(jì)往往需要在滿足指定體積約束下實(shí)現(xiàn)結(jié)構(gòu)動(dòng)響應(yīng)最優(yōu)設(shè)計(jì)。基于上述目標(biāo)函數(shù),結(jié)構(gòu)穩(wěn)態(tài)與瞬態(tài)動(dòng)力學(xué)拓?fù)鋬?yōu)化問題列式可以表達(dá)為

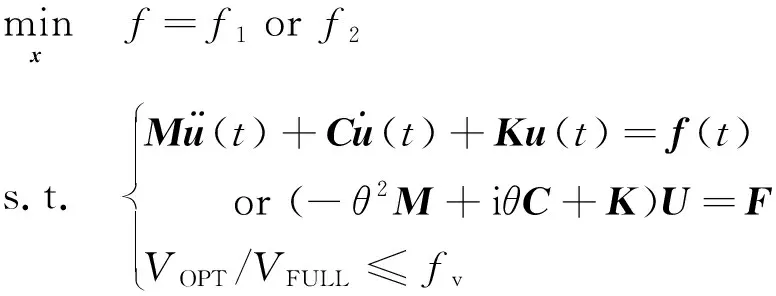
(5)

式中：和分別表征最優(yōu)設(shè)計(jì)允許的材料用量和設(shè)計(jì)域滿布材料時(shí)材料用量。需要指出的是,式(5)中表示材料的拓?fù)洳季?利用不同的拓?fù)涿枋銎浔磉_(dá)方式有所不同。例如,變密度法往往選取單元或節(jié)點(diǎn)密度描述材料場拓?fù)洳季?而水平集方法則利用水平集函數(shù)描述材料分布。本文將采用材料場級(jí)數(shù)展開策略對(duì)材料布局進(jìn)行表征和降維,并在第2節(jié)中詳述。

2 基于材料場級(jí)數(shù)展開策略的結(jié)構(gòu)非梯度拓?fù)鋬?yōu)化方法

2.1 基于材料場級(jí)數(shù)展開策略的結(jié)構(gòu)拓?fù)浔碚髋c降維映射

基于非梯度優(yōu)化算法的復(fù)雜結(jié)構(gòu)拓?fù)鋬?yōu)化問題求解的必要前提是用少量獨(dú)立的拓?fù)湓O(shè)計(jì)變量實(shí)現(xiàn)復(fù)雜結(jié)構(gòu)拓?fù)涞拿枋?本文采用基于材料場級(jí)數(shù)展開(MFSE)策略對(duì)結(jié)構(gòu)的拓?fù)洳季诌M(jìn)行描述,則實(shí)相材料和空相材料的分布可以通過設(shè)計(jì)域內(nèi)觀察位置的材料場函數(shù)()∈[-1, 1]來表示

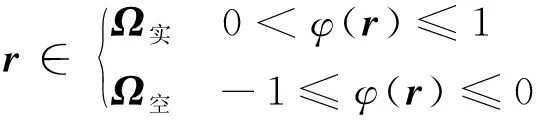
(6)

與傳統(tǒng)的基于單元密度的結(jié)構(gòu)拓?fù)涿枋霾煌?在MFSE描述框架下相鄰2點(diǎn)的材料分布一般不是完全獨(dú)立的(這也符合結(jié)構(gòu)中材料分布的一般規(guī)律),整個(gè)材料場的空間相關(guān)性僅依賴于觀察點(diǎn)的空間相對(duì)位置。因此,需要引入空間中任意2點(diǎn)和的相關(guān)函數(shù)(,)來描述材料場的空間相關(guān)性,這一相關(guān)函數(shù)可以取為

(7)

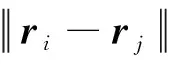
在實(shí)際模擬分析中,需要將無限維材料場離散為觀察點(diǎn),通常在結(jié)構(gòu)設(shè)計(jì)領(lǐng)域內(nèi)均勻分布在個(gè)觀察點(diǎn)上,因此相關(guān)矩陣可以構(gòu)造為

=

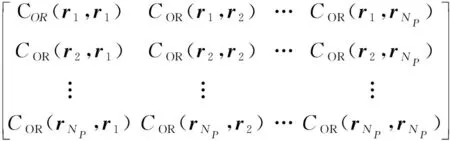
(8)

因此材料場可以進(jìn)一步表示為

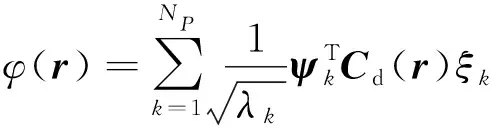
(9)

式中：()=[(,)(,)…(,)];和是相關(guān)矩陣的第階特征值和特征向量;(=1,2,…,)為其中的待定系數(shù),可以理解為廣義的設(shè)計(jì)變量,然而對(duì)于拓?fù)鋬?yōu)化設(shè)計(jì)問題而言,觀察點(diǎn)常分布于結(jié)構(gòu)單元中心(或節(jié)點(diǎn))處,其數(shù)量常達(dá)到數(shù)千甚至數(shù)萬,這一量級(jí)的設(shè)計(jì)變量對(duì)于基于非梯度的優(yōu)化拓?fù)鋬?yōu)化設(shè)計(jì)問題是無法實(shí)現(xiàn)的。因此,在實(shí)際操作中,可將只截取前階特征向量而忽略小特征對(duì),因此材料場可以重新表示為

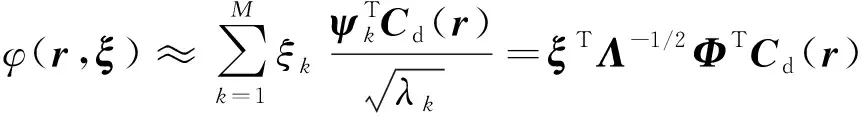
(10)

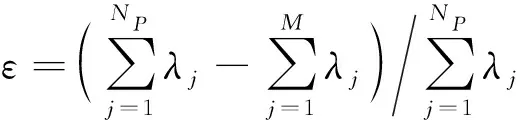
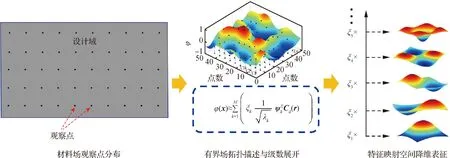
圖1 材料場觀察點(diǎn)分布、有界場拓?fù)涿枋雠c級(jí)數(shù)展開和降維表征示意圖Fig.1 Distribution of observation points, topological description of bounded field, series expansion and dimensionality reduction of material field

為了將基于材料場展開系數(shù)描述的有界材料場映射到整個(gè)設(shè)計(jì)域的所有單元上,且防止結(jié)構(gòu)動(dòng)力學(xué)優(yōu)化中的虛假局部模態(tài)問題,本文引入了(RAMP)Rational Approximation of Material Properties插值模型：

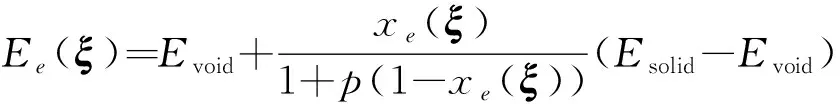
(11)

()=+()(-)

(12)

式中:和分別為單元的楊氏模量和密度;、和、分別表示實(shí)心和空心單元的楊氏模量和密度;為懲罰因子,單元相對(duì)密度變量()可以表示為

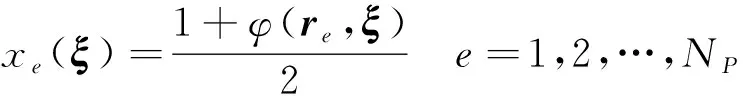
(13)

其中：表示第個(gè)單元的中心坐標(biāo)。這里,為了獲得更光滑的材料密度場分布可以使用Heaviside 函數(shù)進(jìn)行過濾。

基于MFSE方法,式(5)中的穩(wěn)態(tài)和瞬態(tài)動(dòng)力學(xué)拓?fù)鋬?yōu)化問題,可以進(jìn)一步寫成

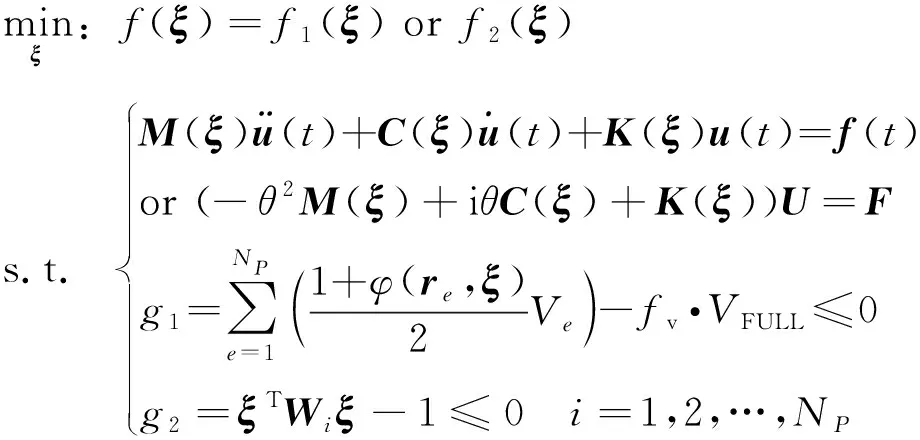
(14)

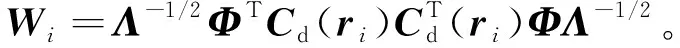
2.2 基于非梯度序列Kriging優(yōu)化算法的拓?fù)鋬?yōu)化問題求解

經(jīng)過基于材料場級(jí)數(shù)展開(MFSE)方法處理,使得拓?fù)鋬?yōu)化設(shè)計(jì)問題中的設(shè)計(jì)變量個(gè)數(shù)大幅度減少,而且單一設(shè)計(jì)變量的改變不只是改變結(jié)構(gòu)拓?fù)浣Y(jié)構(gòu)的某一局部,而是發(fā)生整體的改變。這使得傳統(tǒng)結(jié)構(gòu)拓?fù)鋬?yōu)化問題中設(shè)計(jì)變量過多而無法使用非梯度優(yōu)化算法的難題得到顯著的改善。對(duì)于絕大多數(shù)的結(jié)構(gòu)拓?fù)鋬?yōu)化問題,經(jīng)過MFSE策略對(duì)結(jié)構(gòu)的材料場拓?fù)浔碚髋c降維,可以將結(jié)構(gòu)拓?fù)鋬?yōu)化問題的獨(dú)立設(shè)計(jì)變量降到100個(gè)以內(nèi)(部分問題可以降到50以下),然而這一設(shè)計(jì)變量維度對(duì)于現(xiàn)有的非梯度算法來說,依然具有計(jì)算量大和難以收斂的問題。

針對(duì)結(jié)構(gòu)拓?fù)鋬?yōu)化問題的特性,采用了基于自適應(yīng)策略的序列Kriging算法求解拓?fù)鋬?yōu)化問題。首先將優(yōu)化問題轉(zhuǎn)化為無約束優(yōu)化問題

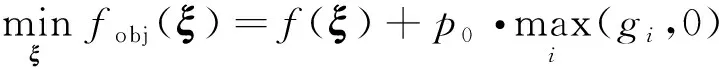
(15)

式中：為障礙乘子。這里障礙乘子并非一個(gè)固定值,與自適應(yīng)障礙因子類似,其取值需要根據(jù)目標(biāo)函數(shù)的大小而改變,實(shí)際算例中這一因子只需要保證約束能夠滿足即可,根據(jù)數(shù)值經(jīng)驗(yàn),障礙因子可以取為=10floor(1+lg|()|),floor(·)表示向下取整。

為了找到無約束優(yōu)化問題的全局解,基于Kriging的算法采用了初始樣本和序列采加點(diǎn)的過程。在代理模型的初始建模中,采用拉丁超立方抽樣,以得樣本在多維設(shè)計(jì)空間中均勻分布。但是采用標(biāo)準(zhǔn)的拉丁超立方采樣方法的過程,會(huì)產(chǎn)生大量無效樣本數(shù)據(jù),這將使基于Kriging的算法很難找到最優(yōu)解。因此,針對(duì)結(jié)構(gòu)拓?fù)鋬?yōu)化問題的基本性態(tài)相對(duì)穩(wěn)定的特性,提出了設(shè)計(jì)變量采樣范圍的自適應(yīng)策略,以提高拓?fù)鋬?yōu)化問題的搜索效率和求解精度,這一自適應(yīng)策略可以有效地防止不切實(shí)際的采樣點(diǎn)的產(chǎn)生。基于自適應(yīng)策略的序列Kriging算法拓?fù)鋬?yōu)化問題求解過程如圖2所示。其自適應(yīng)流程如下：首先,以=為中心,確定初始子設(shè)計(jì)空間,在該設(shè)計(jì)空間中進(jìn)行拉丁超立方采樣和代理模型加點(diǎn)尋優(yōu)。其次,使用當(dāng)前最優(yōu)點(diǎn)(即當(dāng)前代理模型的性能最優(yōu)點(diǎn))以調(diào)整子設(shè)計(jì)空間的中心位置并逐漸減小其范圍,構(gòu)建新的子優(yōu)化問題。隨著子優(yōu)化問題的更新和求解,最終得到優(yōu)化解。

圖2 基于自適應(yīng)策略的序列Kriging算法求解過程示意Fig.2 Solution process diagram of sequential Kriging algorithm based on adaptive strategy

3 算例及結(jié)果討論

3.1 指定頻率區(qū)間結(jié)構(gòu)穩(wěn)態(tài)動(dòng)力學(xué)優(yōu)化算例

一四邊固支的夾層方板結(jié)構(gòu)如圖3所示,夾層板的長度為1.2 m,分為3層。基底層的厚度為0.5 mm,其密度為2 700 kg/m,彈性模量=69×10Pa,泊松比為0.3。阻尼材料層的厚度為3.0 mm,密度為980 kg/m,彈性模量=22×10Pa,泊松比為0.49。約束層的厚度及材料屬性與基底層的厚度、材料屬性一致。方形夾層板的中心處受到一個(gè)集中簡諧激勵(lì)的作用,簡諧激勵(lì)()=ei中=200 N,=2π,載荷頻率區(qū)間為[10, 20] Hz。本文假設(shè)夾層板結(jié)構(gòu)層與層之間完美連接,另外由于基底層和約束層的剛度效應(yīng)遠(yuǎn)大于阻尼材料層的剛度效應(yīng),所以在計(jì)算殼單元?jiǎng)偠汝嚂r(shí)阻尼材料層的偏心效應(yīng)被予以忽略。本算例中,優(yōu)化問題的目標(biāo)函數(shù)為結(jié)構(gòu)加載點(diǎn)動(dòng)柔度的對(duì)數(shù),其表達(dá)式如式(3)所示。

首先將結(jié)構(gòu)劃分為100×100共10 000個(gè)單元的網(wǎng)格,考慮到該方形夾層板結(jié)構(gòu)為對(duì)稱結(jié)構(gòu),取1/4阻尼材料層結(jié)構(gòu)作為優(yōu)化設(shè)計(jì)域,觀察點(diǎn)的個(gè)數(shù)為50×50,獨(dú)立設(shè)計(jì)變量個(gè)數(shù)取=50,體積約束=05。應(yīng)該指出,觀察點(diǎn)的分布可以與有限元網(wǎng)格劃分相互獨(dú)立,通過對(duì)有限元網(wǎng)格加密,理論上將使得分析更為精確。在本文方法的具體實(shí)施過程中,為了方便,觀察點(diǎn)位于每一個(gè)有限單元的中心,即觀察點(diǎn)個(gè)數(shù)等于有限元單元個(gè)數(shù)。相關(guān)長度為0.36 m(設(shè)計(jì)域邊長的0.3倍),當(dāng)相鄰2個(gè)子優(yōu)化問題目標(biāo)函數(shù)之間的相對(duì)誤差小于0.000 1時(shí),優(yōu)化過程停止。從數(shù)值經(jīng)驗(yàn)來看,這一停止準(zhǔn)則的選取將一定程度影響優(yōu)化問題最終的子迭代步個(gè)數(shù)和有限元分析總次數(shù)。當(dāng)這一值取值過小時(shí),在優(yōu)化的中后段優(yōu)化結(jié)果的變化十分微弱,因此只需選擇合適的收斂準(zhǔn)則即能有價(jià)值的優(yōu)化解。

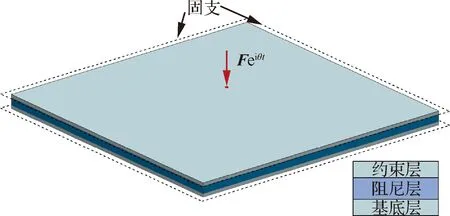
圖3 簡諧荷載作用下的固支夾層板Fig.3 A square plate with four edges clamped under a time-harmonic load

圖4為優(yōu)化迭代歷史曲線,從迭代歷史曲線可以看出,在優(yōu)化的每個(gè)子迭代步中包含2個(gè)階段：① 隨機(jī)采樣階段,在此階段通過拉丁超立方采樣構(gòu)建Kriging代理模型,在此階段迭代歷史出現(xiàn)因隨機(jī)采樣而產(chǎn)生的“振蕩”現(xiàn)象,在本例中每個(gè)子迭代步進(jìn)行3×次隨機(jī)采樣；② 利用EI(Expectation Improvement)加點(diǎn)準(zhǔn)則對(duì)于構(gòu)建的代理模型進(jìn)行尋優(yōu),在此階段優(yōu)化問題的目標(biāo)函數(shù)將平穩(wěn)下降,本算例中對(duì)每個(gè)子迭代步最多進(jìn)行60次加點(diǎn)。在使用Kriging代理模型優(yōu)化算法求解了大約15個(gè)子優(yōu)化問題之后,目標(biāo)函數(shù)收斂。目標(biāo)函數(shù)值從初始設(shè)計(jì)中的365.61 N·m·s穩(wěn)定的下降至優(yōu)化設(shè)計(jì)中的105.68 N·m·s,降幅比較明顯。結(jié)構(gòu)的最終拓?fù)鋬?yōu)化結(jié)果如圖5所示,圖6為結(jié)構(gòu)參考設(shè)計(jì)與優(yōu)化設(shè)計(jì)在0～40 Hz頻域內(nèi)的掃頻曲線,與參考設(shè)計(jì)相比,結(jié)構(gòu)在經(jīng)過優(yōu)化設(shè)計(jì)后,共振峰從給定的頻率區(qū)間內(nèi)(18.6 Hz)移至區(qū)間之外(22.1 Hz),實(shí)現(xiàn)了將結(jié)構(gòu)的共振峰避開特殊頻率區(qū)間的優(yōu)化目的。

圖4 目標(biāo)函數(shù)f1的迭代歷史Fig.4 Iterative history of objective function f1

當(dāng)選取不同的給定頻域區(qū)間時(shí),阻尼材料層的拓?fù)鋬?yōu)化結(jié)果會(huì)發(fā)生變化,圖7給出了指定頻率區(qū)間為[50, 80] Hz的拓?fù)鋬?yōu)化結(jié)果,與指定頻率區(qū)間為[10, 20] Hz的拓?fù)鋬?yōu)化結(jié)果相比,阻尼材料層的拓?fù)洳季肿兊脧?fù)雜,這是因?yàn)楦哳l率的激勵(lì)荷載激發(fā)了結(jié)構(gòu)更為復(fù)雜的局部模態(tài),從而改變了阻尼材料層的拓?fù)洳季帧D8為結(jié)構(gòu)參考設(shè)計(jì)與優(yōu)化設(shè)計(jì)在40～100 Hz頻域內(nèi)的掃頻曲線,可以看出夾層板結(jié)構(gòu)在經(jīng)過優(yōu)化布局后,其共振峰也從給定的頻率區(qū)間內(nèi)移至給定區(qū)間之外。表1給出了考慮載荷頻率區(qū)間為[50, 80] Hz時(shí)的優(yōu)化結(jié)果和參考解的前10階固有頻率對(duì)比列表,可以看出相比于僅考慮[10, 20] Hz的動(dòng)力學(xué)優(yōu)化相比,考慮[50, 80] Hz頻率區(qū)間的優(yōu)化問題包含了結(jié)構(gòu)更高階的固有頻率,其頻率區(qū)間內(nèi)的動(dòng)力學(xué)優(yōu)化減振體現(xiàn)了多個(gè)振動(dòng)模態(tài)下的綜合減振效應(yīng)。與已有阻尼減振結(jié)構(gòu)拓?fù)鋬?yōu)化相比,針對(duì)同樣的問題本文的優(yōu)化結(jié)果與已有方法十分相似,說明本文方法計(jì)算結(jié)果具有正確性。

圖5 阻尼材料層優(yōu)化結(jié)果(頻率區(qū)間[10, 20] Hz)Fig.5 Optimization result of damping layer (frequency range[10, 20] Hz)

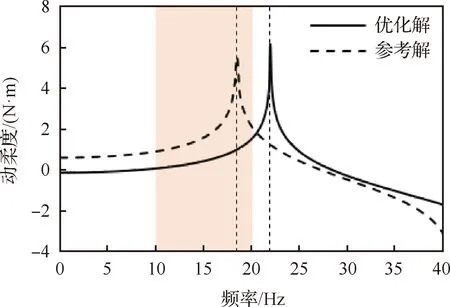
圖6 結(jié)構(gòu)指定位置的掃頻曲線優(yōu)化解(頻率區(qū)間[10, 20] Hz)與參考解(ρe=0.5)的比較Fig.6 Comparison between optimal solution (frequency range[10, 20] Hz) and reference solution (ρe=0.5) of sweep curve at specified position of structure

圖7 阻尼材料層優(yōu)化結(jié)果(頻率區(qū)間[50, 80] Hz)Fig.7 Optimization result of damping layer (frequency range[50, 80] Hz)

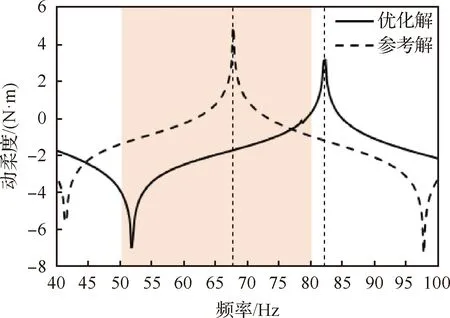
圖8 結(jié)構(gòu)指定位置的掃頻曲線優(yōu)化解(給定頻率區(qū)間[50, 80] Hz)與參考解(ρe=0.5)的比較Fig.8 Comparison between optimal solution (given frequency range[50, 80] Hz) and reference solution (ρe=0.5) of sweep curve at specified position of structure

表1 優(yōu)化結(jié)構(gòu)與參考結(jié)構(gòu)各階固有頻率比較

在運(yùn)載航天器系統(tǒng)中,載荷適配器可以為載荷與航天器之間提供一個(gè)緩沖截面。通過在載荷適配器表面鋪設(shè)阻尼層可以減小航天器與衛(wèi)星之間的振動(dòng)。本文載荷適配器結(jié)構(gòu)由圓柱段、圓錐臺(tái)段與法蘭3部分構(gòu)成,其上部的直徑為500 mm,底部的直徑為700 mm,如圖9所示。圓柱段的高度和厚度分別為200 mm和1.5 mm,圓錐臺(tái)段的高度與厚度分別為200 mm和0.8 mm,法蘭的外直徑為740 mm,厚度為2 mm。結(jié)構(gòu)的圓錐臺(tái)段鋪設(shè)阻尼層,厚度為1 mm,結(jié)構(gòu)基底與阻尼的材料屬性與算例1一致。

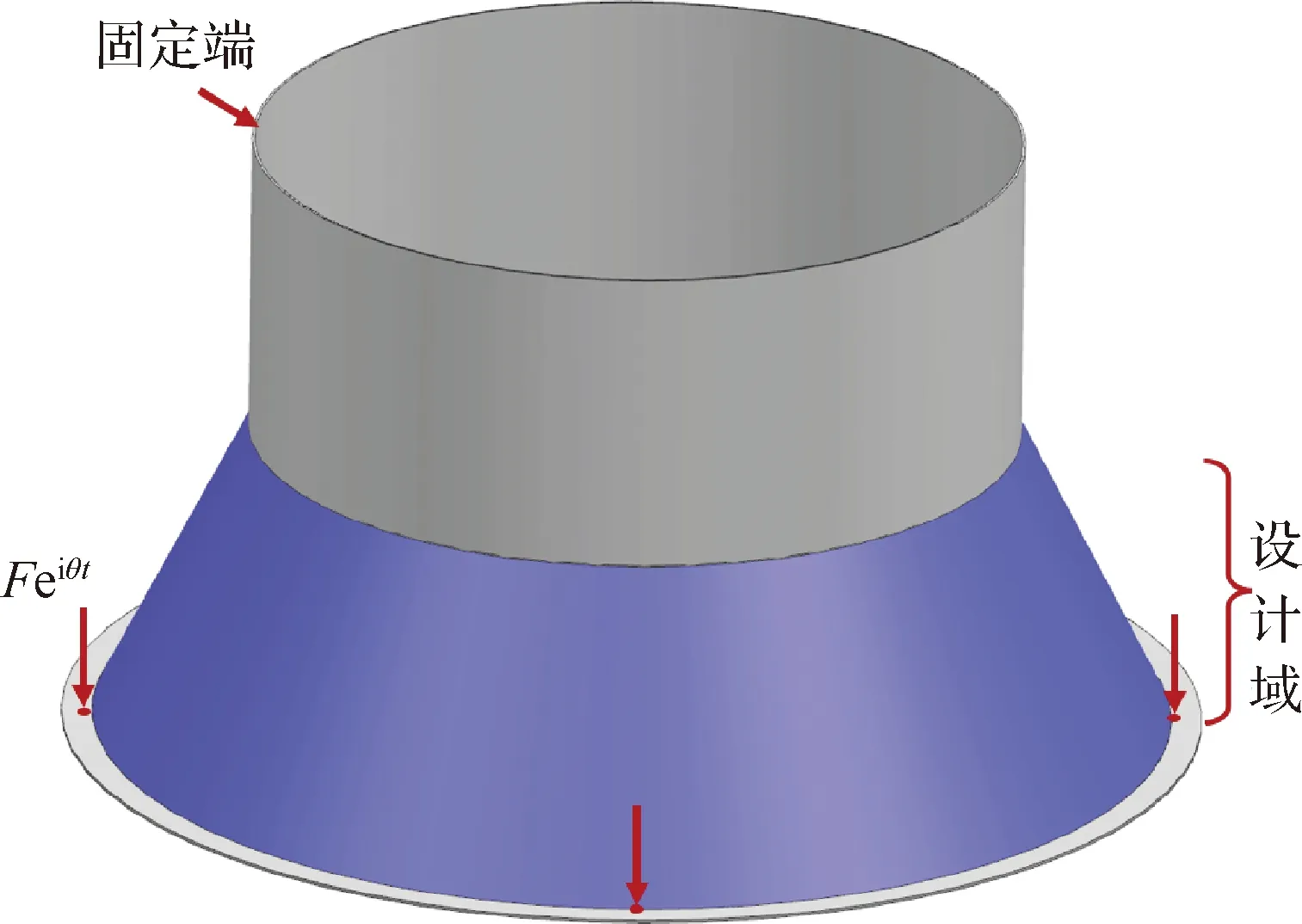
圖9 簡諧激勵(lì)下載荷適配器示意圖Fig.9 Payload adapter subjected to four harmonic concentrated forces

結(jié)構(gòu)整體劃分為240×50個(gè)有限元單元,對(duì)于此周向循環(huán)結(jié)構(gòu),取阻尼層的周向1/4作為優(yōu)化設(shè)計(jì)域,觀察點(diǎn)的個(gè)數(shù)為60×30,設(shè)計(jì)變量個(gè)數(shù)為50,相關(guān)長度取為阻尼層母線長度的0.3。圓柱段的頂部受到固定約束,4個(gè)簡諧激勵(lì)等距地加載在法蘭底部內(nèi)側(cè)的縱向,其幅值為=10 kN,載荷頻率區(qū)間為[360, 420] Hz, 設(shè)計(jì)要求在荷載頻域內(nèi)無共振峰值。設(shè)計(jì)域體積約束上限為=05,優(yōu)化問題的目標(biāo)函數(shù)取為4個(gè)加載點(diǎn)動(dòng)柔度之和。優(yōu)化結(jié)果如圖10所示,圖11 為參考解(=05)與優(yōu)化解的掃頻曲線比較。

圖10 阻尼材料層拓?fù)鋬?yōu)化結(jié)果Fig.10 Optimization result of damping layer

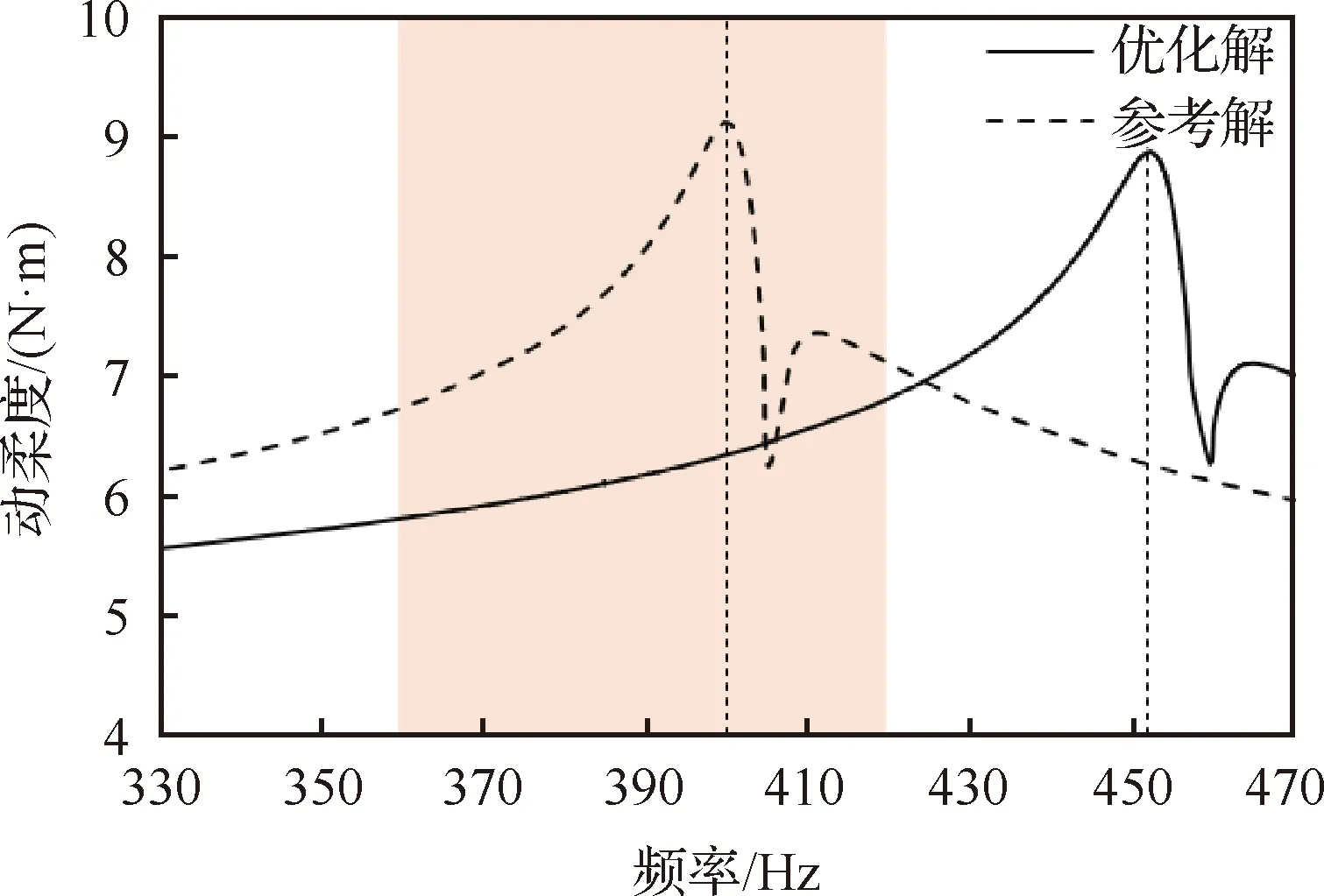
圖11 結(jié)構(gòu)指定位置的掃頻曲線優(yōu)化解與參考解(ρe=0.5)比較Fig.11 Comparison between optimal solution and reference solution (ρe=0.5) of sweep curve at specified position of structure

3.2 瞬態(tài)動(dòng)力載荷結(jié)構(gòu)拓?fù)鋬?yōu)化算例

如圖12所示,懸臂矩形夾層板的尺寸為0.6 m×0.4 m,由厚度為1.0 mm的阻尼材料層與厚度均為0.5 mm的基底層和約束層組成。該夾層板結(jié)構(gòu)各層的材料屬性與算例1夾層板結(jié)構(gòu)各層的材料屬性一致。夾層板的自由邊中點(diǎn)受到?jīng)_擊荷載()的作用,其時(shí)程曲線如圖13 所示。在該算例中目標(biāo)函數(shù)所考慮的時(shí)間段終止時(shí)刻為=0.05 s,時(shí)域積分方法的時(shí)間步長Δ=2×10s。

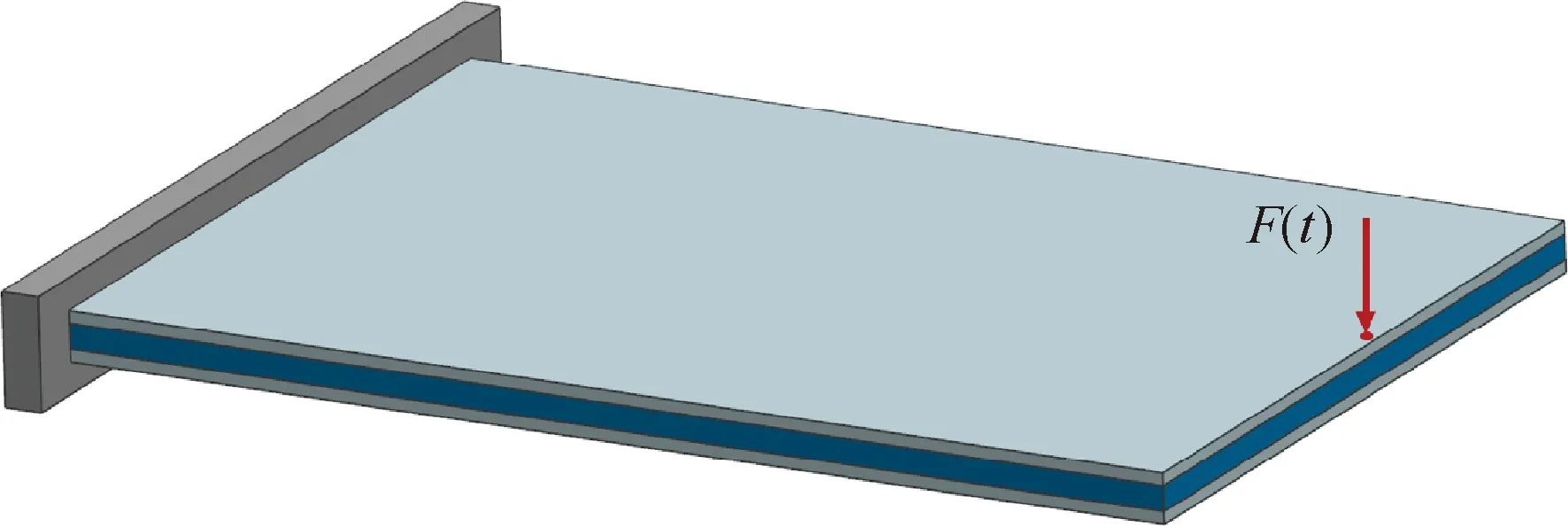
圖12 沖擊荷載作用下的懸臂夾層板Fig.12 A cantilever plate under impact load

整個(gè)結(jié)構(gòu)被劃分為60×40個(gè)單元,相關(guān)長度為0.12 m(設(shè)計(jì)域短邊的0.3倍),設(shè)計(jì)變量個(gè)數(shù)取=50,阻尼材料的體積約束分?jǐn)?shù)取=05。優(yōu)化問題的目標(biāo)函數(shù)取為自由邊中點(diǎn)振幅的平方在時(shí)間段[0,]內(nèi)的積分。本算例中,目標(biāo)函數(shù)為結(jié)構(gòu)指定位置瞬態(tài)的動(dòng)響應(yīng),其表達(dá)式如式(4)所示。

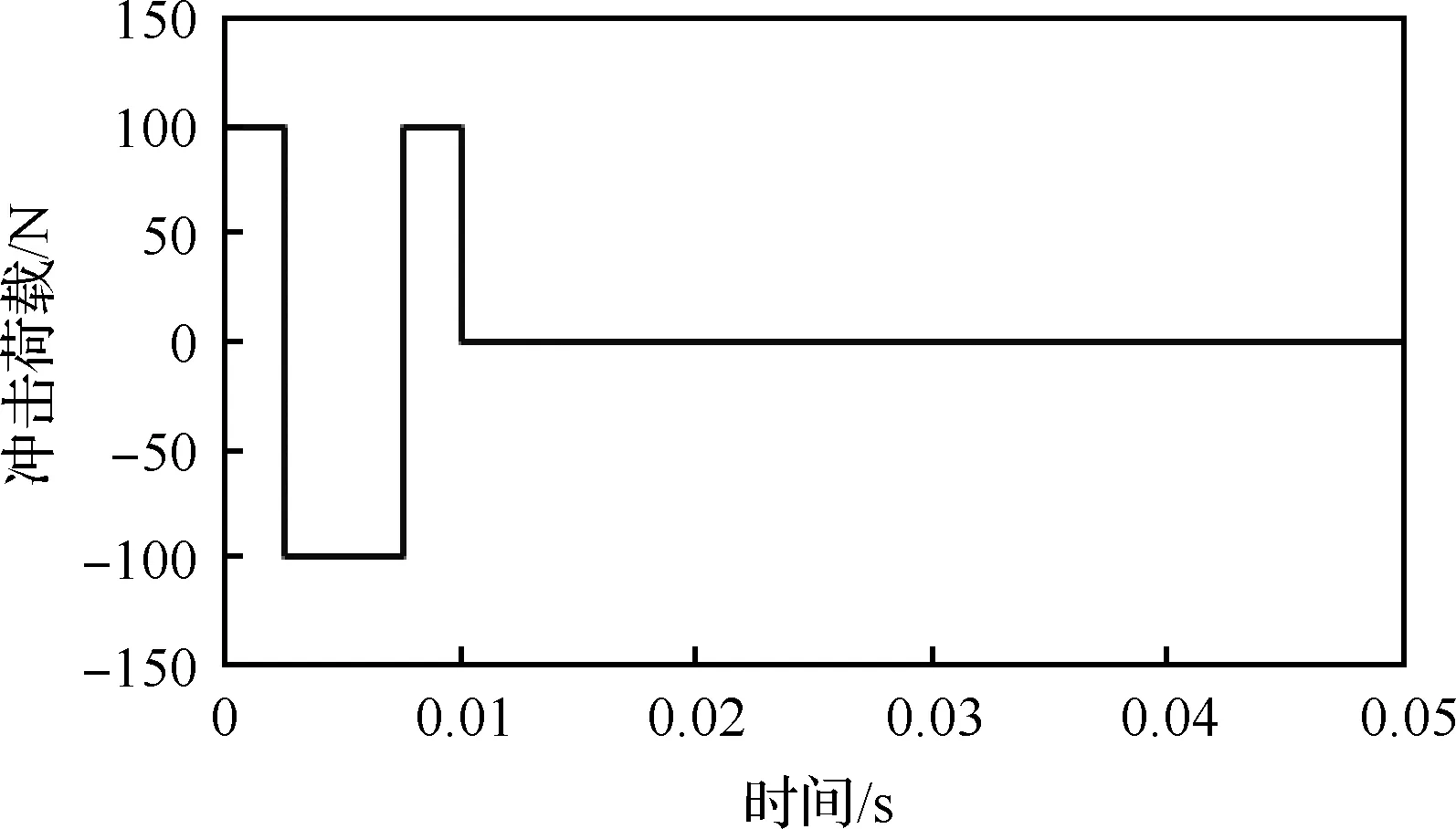
圖13 懸臂夾層板沖擊荷載時(shí)程曲線Fig.13 Impact force applied to cantilever plate

優(yōu)化迭代曲線如圖14所示,優(yōu)化過程在經(jīng)過15個(gè)子迭代步,共2 749步迭代后收斂,目標(biāo)函數(shù)從初始設(shè)計(jì)中的10.97 m·s平穩(wěn)的下降至4.78 m·s,下降了56.43%。圖15為最終的阻尼材料層拓?fù)鋬?yōu)化布局。初始設(shè)計(jì)和優(yōu)化設(shè)計(jì)的目標(biāo)位置時(shí)程位移響應(yīng)如圖16所示,可以發(fā)現(xiàn)結(jié)構(gòu)在經(jīng)過優(yōu)化設(shè)計(jì)后,其振動(dòng)幅值有明顯的降低,振動(dòng)頻率也低于結(jié)構(gòu)初始設(shè)計(jì)的振動(dòng)頻率,這說明拓?fù)鋬?yōu)化解良好地實(shí)現(xiàn)了結(jié)構(gòu)振動(dòng)控制。

圖14 目標(biāo)函數(shù)f2的迭代歷史Fig.14 Iterative history of objective function f2

圖15 阻尼材料層拓?fù)鋬?yōu)化結(jié)果(T=0.05 s)Fig.15 Optimization result of damping layer (T=0.05 s)

修改時(shí)間段終止時(shí)刻為0.2 s,其優(yōu)化結(jié)果如圖17所示。可以看出,當(dāng)改變目標(biāo)函數(shù)所考慮的時(shí)間段終止時(shí)刻,拓?fù)鋬?yōu)化結(jié)果發(fā)生了明顯的變化。圖18為初始設(shè)計(jì)與優(yōu)化設(shè)計(jì)的目標(biāo)位置位移時(shí)程響應(yīng),可以發(fā)現(xiàn)結(jié)構(gòu)在經(jīng)過優(yōu)化設(shè)計(jì)后,在時(shí)間歷程前期其振動(dòng)衰減得更加迅速,在時(shí)間歷程后期其振動(dòng)趨于平穩(wěn)。

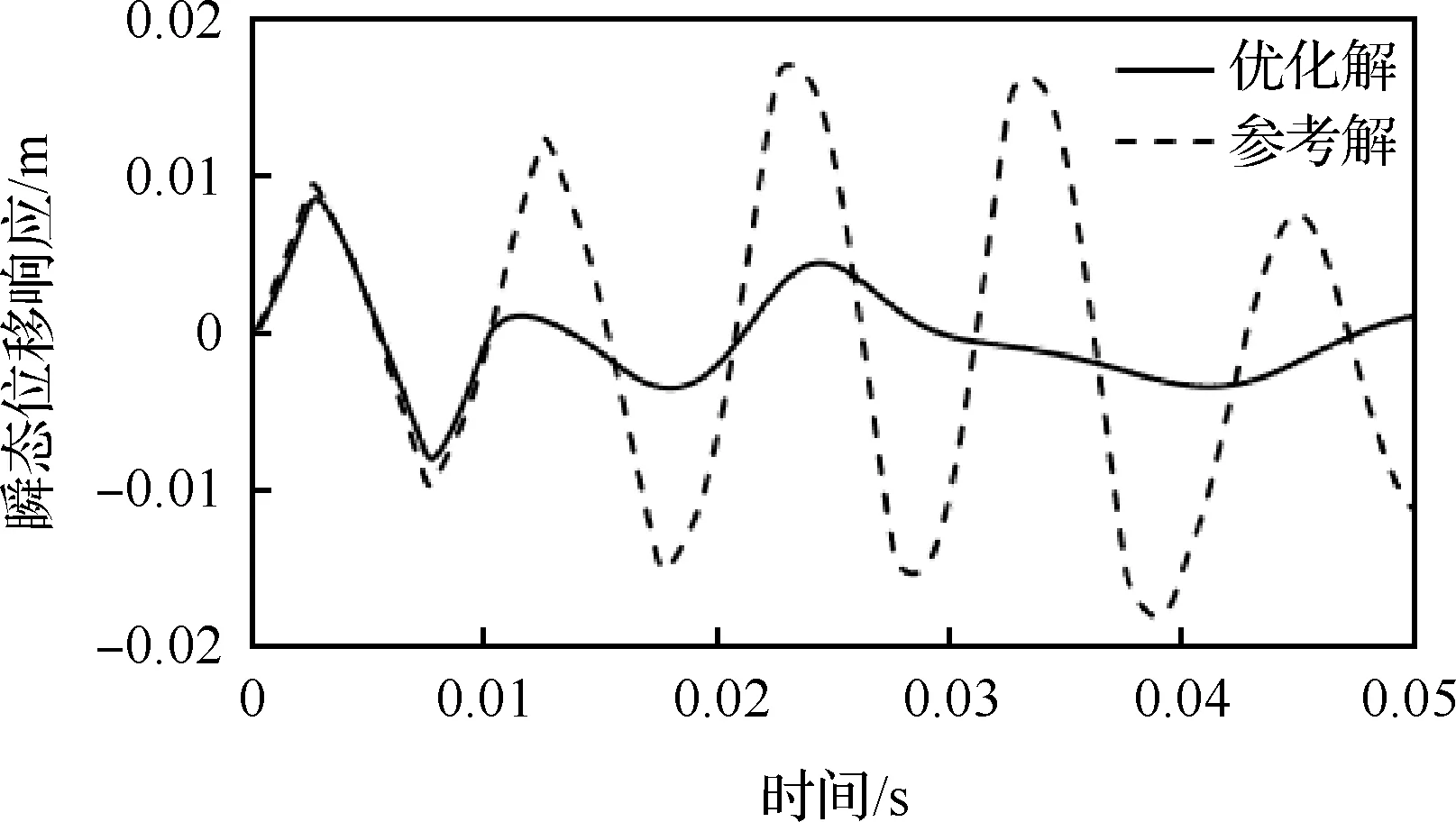
圖16 結(jié)構(gòu)指定位置位移時(shí)程響應(yīng)的優(yōu)化解(T=0.05 s)與參考解(ρe=0.5)比較Fig.16 Comparison between optimal solution (T=0.05 s) and reference solution (ρe=0.5) for displacement time history response of structures at specified positions

圖17 阻尼材料層拓?fù)鋬?yōu)化結(jié)果(T=0.2 s)Fig.17 Optimization result of damping layer (T=0.2 s)

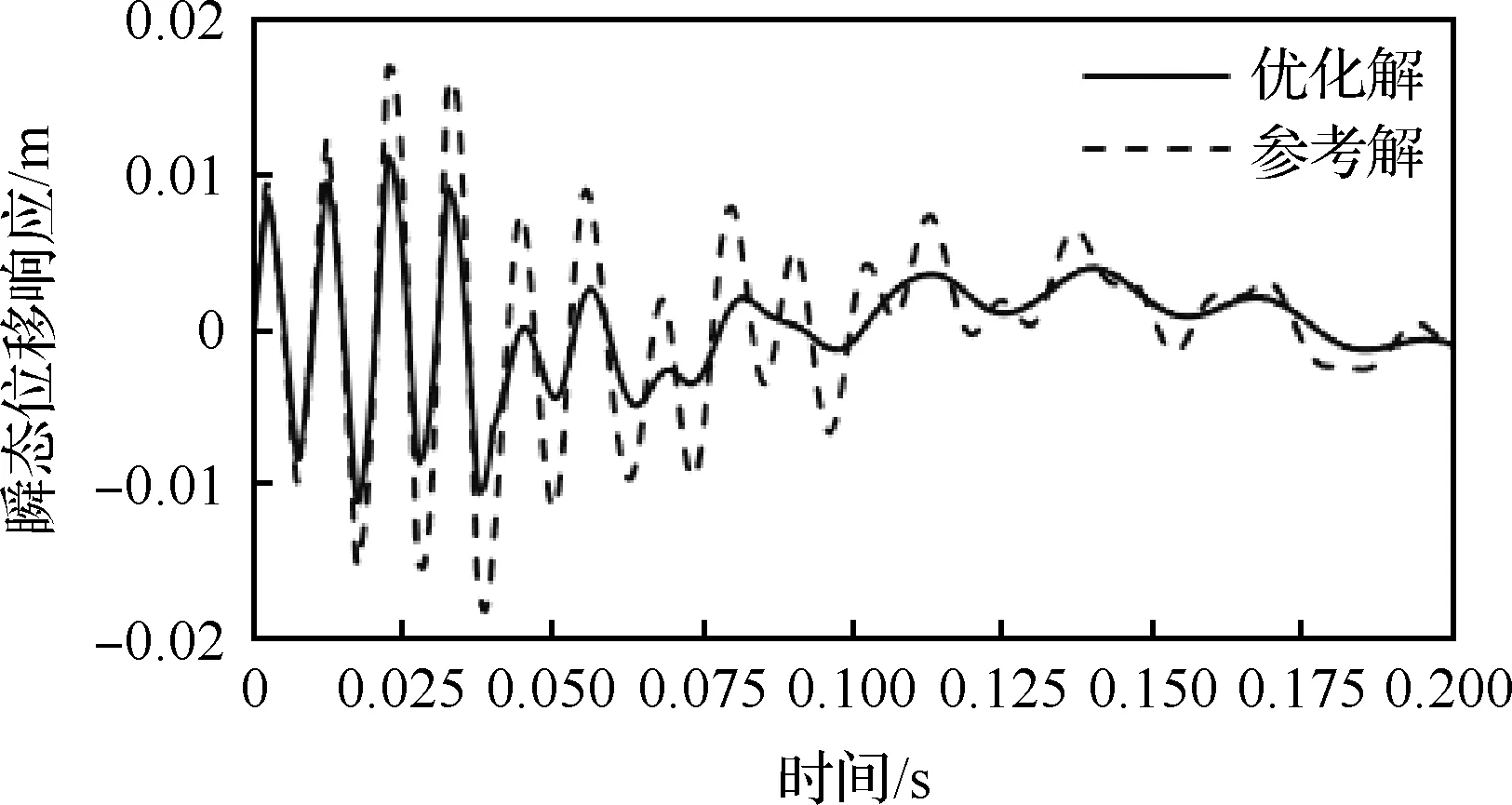
圖18 結(jié)構(gòu)指定位置位移時(shí)程響應(yīng)的優(yōu)化解(T=0.2 s)與參考解(ρe=0.5)比較Fig.18 Comparison between optimal solution (T=0.2 s) and reference solution (ρe=0.5) for displacement time history response of structures at specified positions

4 結(jié) 論

本文研究了基于材料場級(jí)數(shù)展開策略的結(jié)構(gòu)動(dòng)力學(xué)非梯度拓?fù)鋬?yōu)化方法,該方法能夠利用少量拓?fù)鋱雒枋鲎兞繉?shí)現(xiàn)復(fù)雜結(jié)構(gòu)的拓?fù)浔碚?從而大幅降低結(jié)構(gòu)拓?fù)鋬?yōu)化變量個(gè)數(shù),進(jìn)一步采用自適應(yīng)序列Kriging代理模型算法求解拓?fù)鋬?yōu)化問題,實(shí)現(xiàn)了基于非梯度優(yōu)化算法的大規(guī)模結(jié)構(gòu)動(dòng)力學(xué)拓?fù)鋬?yōu)化問題的求解。所提方法因不需要靈敏度信息,使得優(yōu)化問題目標(biāo)函數(shù)和約束函數(shù)的選取與以往動(dòng)力學(xué)優(yōu)化問題相比具有更大的自由度,更適用于復(fù)雜動(dòng)力學(xué)優(yōu)化問題的建模與求解。數(shù)值算例表面,所提優(yōu)化問題能很好地處理結(jié)構(gòu)在穩(wěn)態(tài)與瞬態(tài)動(dòng)力學(xué)荷載下的拓?fù)鋬?yōu)化問題。

本文所處理的2類優(yōu)化問題設(shè)計(jì)目標(biāo),屬于常規(guī)結(jié)構(gòu)動(dòng)力學(xué)優(yōu)化目標(biāo),可以通過靈敏度分析和梯度算法進(jìn)行求解和設(shè)計(jì),但考慮頻率區(qū)間或時(shí)間段內(nèi)的振動(dòng)優(yōu)化問題中,由于原目標(biāo)函數(shù)不連續(xù),常常需要引入包絡(luò)函數(shù)等技術(shù),使得靈敏度更為復(fù)雜,部分優(yōu)化問題采用基于梯度的優(yōu)化算法因多局部解效應(yīng)導(dǎo)致收斂性較差。同時(shí),該方法因不需要靈敏度信息,易與各種仿真分析軟件結(jié)合,未來在復(fù)雜物理場和非線性結(jié)構(gòu)拓?fù)鋬?yōu)化問題(如多物理場、非線性優(yōu)化、接觸與碰撞)中,具有較大的應(yīng)用前景,目前已經(jīng)在聲學(xué)與光學(xué)超材料設(shè)計(jì)、大變形結(jié)構(gòu)拓?fù)鋬?yōu)化、流固耦合問題優(yōu)化等方面進(jìn)行了初步嘗試。

值得注意的是,此前已有文獻(xiàn)給出了10萬以上自由度的工程結(jié)構(gòu)算例,本文所提出的基于材料場級(jí)數(shù)展開的結(jié)構(gòu)拓?fù)鋬?yōu)化方法需要的總計(jì)算次數(shù)(有限元分析)與傳統(tǒng)梯度類優(yōu)化算法相比較多。然而,隨著計(jì)算機(jī)硬件技術(shù)和并行計(jì)算能力的飛速發(fā)展,本文在未來大規(guī)模動(dòng)力學(xué)優(yōu)化問題仍然有較大的應(yīng)用潛力。