基于改進CNN的壓縮感知自然圖像重建方法

許富景， 陳長穎， 杜少成

(1. 山西大學自動化與軟件學院，山西 太原 030013; 2. 山西大學數學科學學院，山西 太原 030006)

0 引 言

隨著壓縮感知（compressed sensing，CS）及其重建方法的不斷發展[1-2]，該方法被廣泛應用在遙測遙感、海洋探測、醫療影像等三維圖像重建領域[3-5]，并且推動了相關領域新型成像設備的研制[6-7]。然而，傳統壓縮感知圖像重建算法存在著壓縮率低、所需存儲空間量大等問題[8]，尤其在高清成像領域，圖像大數據給存儲空間帶來巨大的挑戰，分塊壓縮感知理論[9]的提出大大減少了所需的存儲空間。為了進一步提高圖像的重建質量，Dinh等人提出了一種新的測量矩陣[10]來改善低采樣率下圖像的重建精度，Gao等人結合圖像的局部平滑特點設計出局部結構測量矩陣[11]使得圖像的重建精度得到明顯提升。

基于神經網絡的壓縮感知圖像重建算法能夠有效改善圖像的重建性能。Mousavi等人首次提出利用堆疊式降噪自動編碼器(SDA)[12]從少量測量向量中重建圖像的方法取得了很好的重建效果。文獻[13]在重建階段使用卷積從高斯測量向量中重建圖像，在其網絡結構基礎上，文獻[14]在重構階段引入殘差網絡來縮小初始重建圖像與原圖像之間的差距進而得到更高的重建精度。Dong等人利用卷積神經網絡(CNN)[15]通過端到端的學習方式從低分辨率圖像中重建出高分辨率圖像。上述這些重建方法均利用隨機測量向量來重建圖像，而隨機測量向量不能有效保留原信號的主要信息，為此，自適應測量向量被人們提出來。Wang等人使用深度神經網絡[16]來模擬信號的稀疏編碼過程，獲得的測量向量中保留了原圖像的更多有用信息。Xie等人利用全連接層[17]獲得從原始信號中學習得來的自適應測量向量，利用該測量向量重建出來的圖像的PSNR值有明顯的提高。然而，由于全連接層的參數冗余，利用全連接層獲得測量向量的方法不僅增加了運算時間還容易造成過擬合。

針對上述問題，本文提出了一種基于改進CNN的壓縮感知自然圖像重建方法，該方法將傳統壓縮感知圖像重建算法與卷積神經網絡相結合，它的主要創新思路如下：首先采用卷積網絡自適應獲得測量向量，這比采用傳統壓縮感知測量矩陣（隨機高斯、伯努利等）得到的隨機測量向量更多地保留了原圖像的主要信息。其次，在初始重建階段使用的子像素卷積網絡的放大倍數是通過訓練、學習得到的，其放大性能比傳統的雙線性插值、雙三次插值及反卷積網絡等更加準確，從而重建出了更高質量的圖像。最后，利用深度殘差網絡進一步縮小初始重建圖像與原圖像之間的殘差，該方法有效提升了傳統壓縮感知圖像重建方法的重建精度。

1 基礎理論

1.1 壓縮感知圖像重建的測量矩陣

壓縮感知理論打破了傳統奈奎斯特采樣定理最低采樣頻率的局限，當信號能被稀疏表示時，壓縮感知理論可以利用亞采樣得到的少量測量向量重建原信號。壓縮感知理論的觀測過程將采樣和壓縮集為一體，測量矩陣的設計關系著測量向量和重建信號的質量，它必須滿足約束等距性質(RIP)[18]。圖1所示的壓縮感知原理圖中存在如下等式關系：

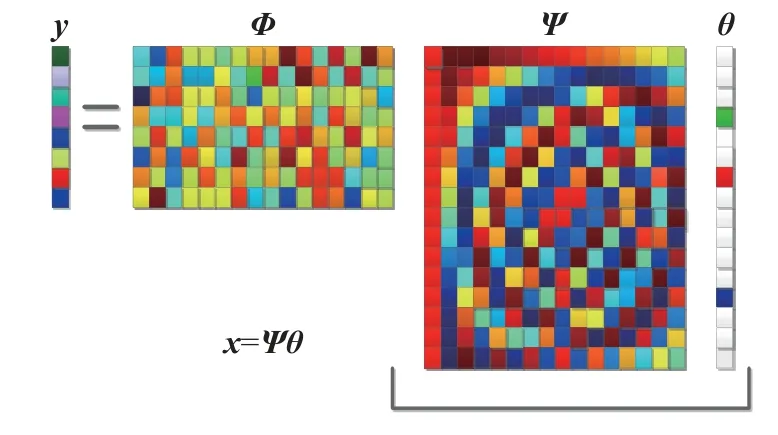
圖1 壓縮感知原理圖

其中，y∈RM×1,x∈RN×1,Φ∈RM×N。

測量向量y中 的元素可看作是原信號x通過觀測矩陣Φ從高維空間到低維空間的線性映射，因此測量向量y中保留了原信號的有用信息能夠用來重建原信號。若原信號x在 稀疏域Ψ 上為K階稀疏信號，則x在Ψ域上可以表示為：

將等式(2)代入等式(1)中有：

其中，等式（3）中常見的觀測矩陣Φ有隨機高斯矩陣、隨機伯努利矩陣等。

1.2 壓縮感知傳統的重建算法

傳統壓縮感知理論重建算法包括貪婪算法[19-20]、凸優化算法[21]和迭代算法[22]。這些重建算法通過測量矩陣Φ得到測量向量y， 利用M維的測量向量y和測量矩陣Φ求 解出N維的原信號x。 由于M?N，所以不能通過直接逆向求解等式(1)來求出原信號x的唯一解。然而，當原信號x在某個變換域Ψ上有稀疏信號θ，它的稀疏度為K且滿足K?M，那么可根據等式(3)求解出稀疏信號θ,再結合等式(2)便求出原信號x，即傳統重建算法是將高維的原信號線性映射到某變換域后得到原信號的稀疏表示再進行優化求解，該過程可表示為求公式(4)中的優化目標：

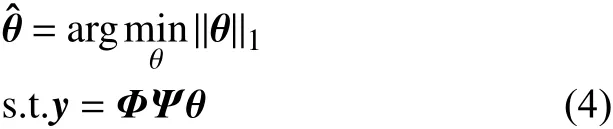
這種通過迭代方式求優化解的重建算法的計算復雜度高并且在低采樣率下圖像的重建精度很低。近幾年，結合卷積神經網絡的壓縮感知圖像重建算法在重建圖像任務中發揮了很好的作用。

1.3 卷積神經網絡基礎理論

卷積神經網絡是常見的深度學習算法之一，它是一個多層網絡結構能夠自動提取圖像特征，還可以直接把圖像作為輸入使多維圖像處理更加簡便，因而被廣泛應用在圖像處理領域。卷積神經網絡結構圖如圖2所示，它的運算主要有：卷積運算、池化運算、全連接運算和識別運算。卷積運算通過卷積核與輸入的圖像做卷積得到特征值，由于卷積運算屬于線性操作而實際的圖像處理多為非線性問題，故需要在卷積層后加入激活函數層，以此來增加卷積運算的非線性擬合能力并加快訓練網絡模型，常用的激活函數有ReLU、Tanh和PReLU，它們的函數分別對應如下：

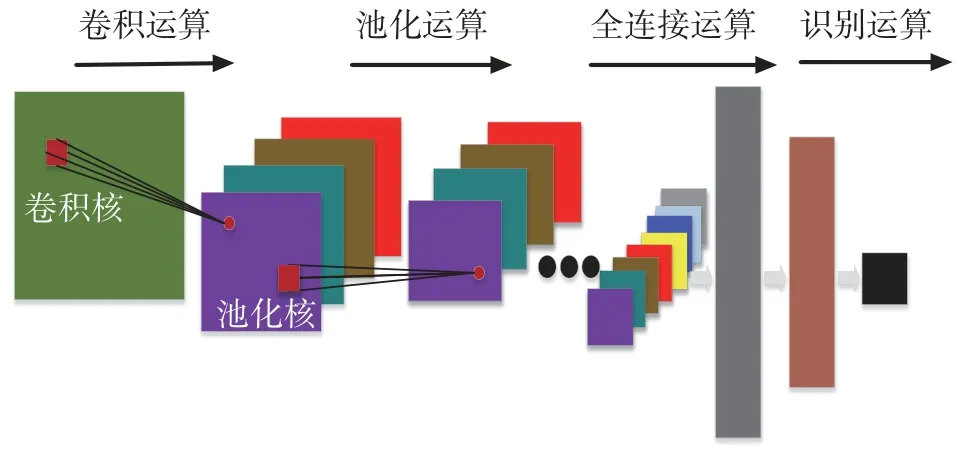
圖2 卷積神經網絡結構圖

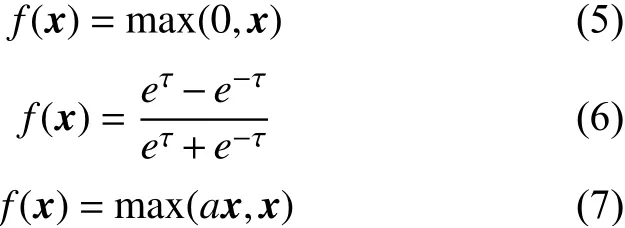
卷積運算的過程可以表示為：

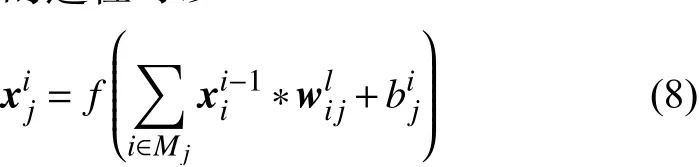
式中：xij——當前層的特征映射；

f(·)——激活函數；

xii-1——上層特征映射；

wiij——第l層 ，(i,j)位置的權重；

bij——偏置。

池化運算可看作是對上一運算結果做進一步的特征提取和壓縮，常用的池化類型有最大池化和平均池化，最大池化輸出局部接受域的最大值，該過程可表示為：

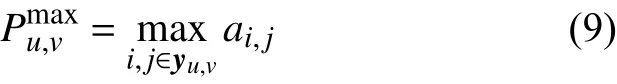
平均池化輸出局部接受域的平均值，該過程可表示為：

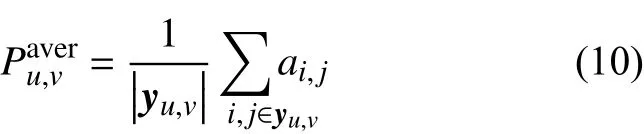
式中：yu,v——池化運算對應的特征圖上的區域；

i,j——索引；

ai,j——池化的激活值。

池化運算對卷積的運算結果做了特征降維，使模型的容錯性得到提高并有效緩解過擬合。

全連接運算對前面提取的特征進行分類起到分類器的作用，它把卷積和池化運算的結果進行組合并提取整合輸出的有用信息，把信息從高維變換到低維，然而全連接層的參數過多會增加運算時間并容易造成過擬合。

卷積神經網絡輸入與輸出之間本質上可以看作是一種映射關系，通過訓練可以把圖像中的主要信息提取整合并將數據特征映射保留在神經網絡中。

2 基于改進CNN的壓縮感知重建算法

2.1 結合卷積神經網絡的壓縮感知重建算法

壓縮感知圖像重建算法的目的是從測量向量y中重建原信號x， 其中，y∈RM×1,x∈RN×1。因為M?N，所以同一個測量向量y可以重建出多個不同的信號x。 把從y到x的映射近似看作線性映射，該映射關系可以表示為：

其中W∈RN×M是線性映射矩陣，方程y=Φx(M?N)不是唯一解。原信號和它相對應的測量向量分別表示為：xi∈RN×1,yi∈RM×1， 把包含N個訓練樣本的訓練集表示為：{(y1,x1),(y1,x1),···,(yN,xN)}。通過評估映射矩陣Wf來保證的偏差最小。損失函數如式（12）所示：

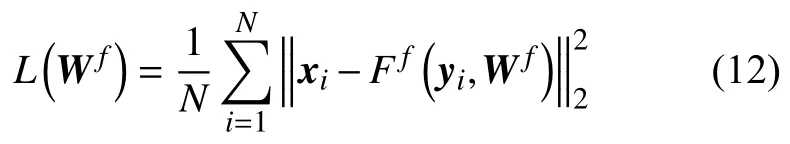
式中：xi——第i個原信號(訓練樣本)；

N——訓練集中的樣本總數。

利用自適應矩估計優化算法(Adam)[23]優化網絡模型參數并通過反向傳播來最小化損失函數，可以得到最優映射矩陣Wf

和等式(13)中訓練樣本所對應的自適應測量向量yi：

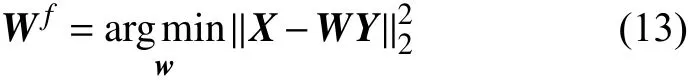
基于卷積神經網絡的壓縮感知自然圖像重建算法結構示意圖如圖3所示，其第一個卷積層后面引入最大池化層來壓縮圖像，最大池化層可以輸出局部接受域中的最大值能更好保留圖像的紋理特征，因此被廣泛應用在圖像處理領域，它的原理為：首先利用卷積網絡自適應獲得測量向量yi， 把yi作為初始重建階段子像素卷積的輸入并恢復出低分辨率初始重建圖像，生成初始重建圖像的過程可以表示為：

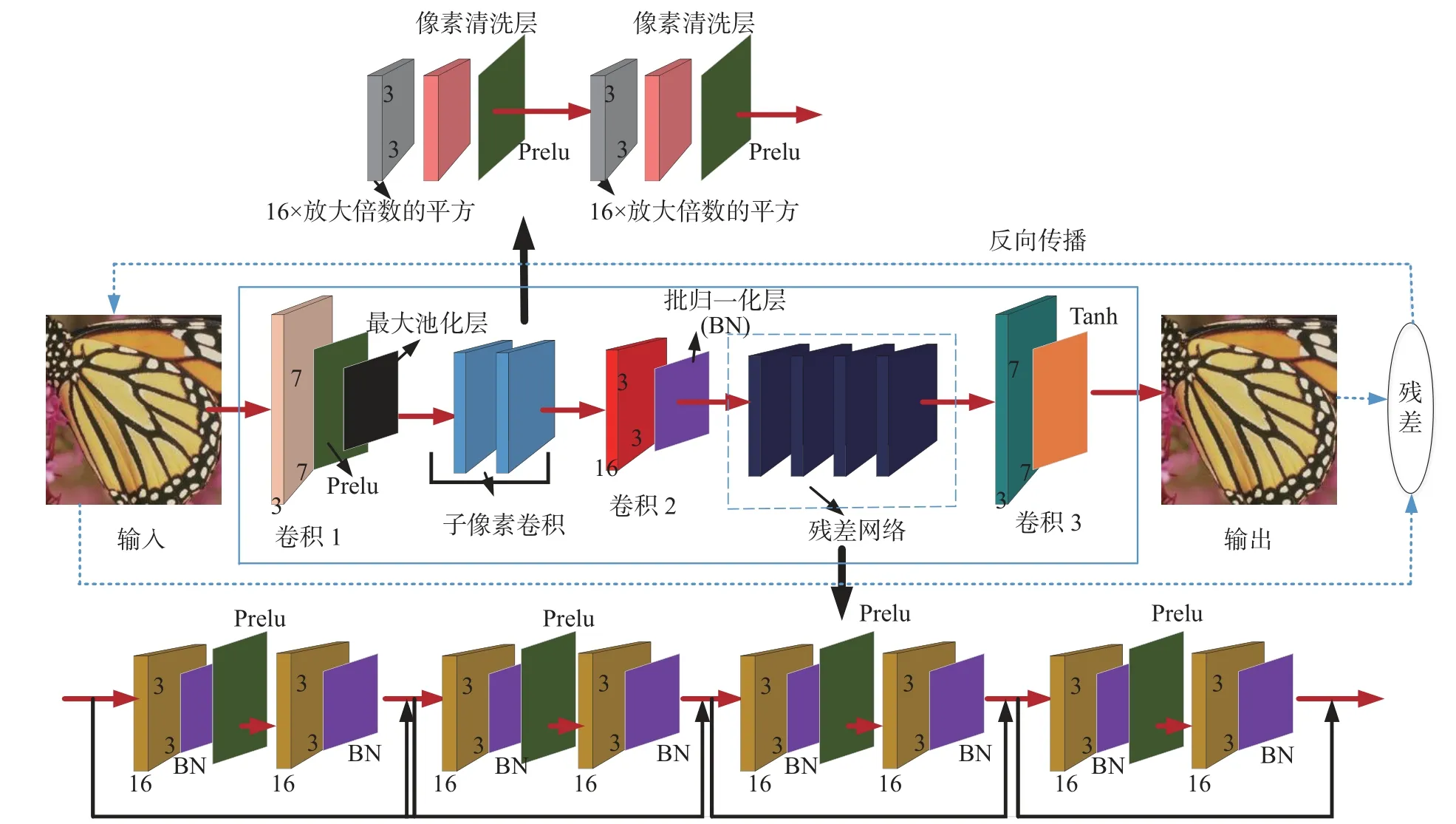
圖3 基于改進CNN的壓縮感知自然圖像重建算法結構示意圖

其次，為進一步縮小初始重建圖像與原圖像xi之 間的誤差，在它們之間引入殘差網絡Fr(,Wr)來估計差值， 其中，是Wr殘差網絡的參數，該過程可以表示為：

將初始重建圖像與從殘差網絡得到的殘差估計值相融合，該過程可以表示為：

把和分別代入等式(14)和等式(15)中便得到經過殘差網絡改善后的重建圖像，該過程可以表示為：

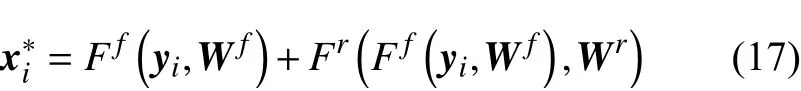
2.2 子像素卷積網絡

子像素卷積原理圖如圖4所示，子像素卷積利用像素清洗層將輸入圖像的像素重新排列從而實現對圖像的上采樣運算[24]。當一個上采樣操作的放大倍數為r時，子像素卷積需要輸入r2個由圖像構成的同等大小的特征張量。上采樣后的圖像上位于(x,y)處 像素的值由第c張特征圖中位于處的像素點。該過程可以表示為：

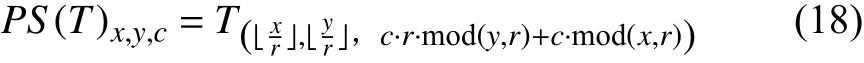
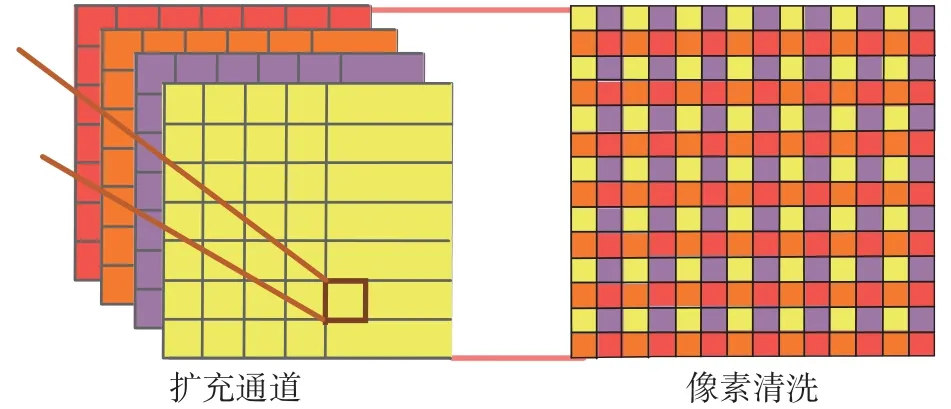
圖4 子像素卷積原理圖

假設要利用子像素卷積進行縮放因子為r的上采樣操作，記上采樣之前特征圖的大小為:H×W×C，首先通過卷積運算輸出大小為rH×r2W×C的特征圖，然后經過像素清洗層將特征圖的大小調整為:rH×rW×C，如：要利用子像素卷積將二維圖像放大2倍，則需要生成(22=4)4個同等大小的特征圖，即通道數被擴充為原來的4倍。特征圖的大小調整為:rH×rW×C，如：要利用子像素卷積將二維圖像放大2倍，則需要生成(22=4)4個同等大小的特征圖，即通道數被擴充為原來的4倍。特征圖做完卷積后再經過像素清洗層作特定排列，像素清洗后的特征通道數又恢復為初始輸入時的大小，而每個特征圖的尺寸則會變大為原來的2倍。

本文使用子像素卷積來初始重建圖像，其結構圖如圖5所示。該子像素卷積網絡由兩個結構相同的子像素卷積模塊組成，每個子像素卷積模塊包括一個卷積層、一個像素清洗層和一個激活函數PReLU層。由于子像素清洗層能確保前面的卷積運算在低分辨率空間上運行所以減少了卷積的運算時間，而激活函數的使用給神經網絡中引入了非線性特性使得輸出不再只是輸入的線性組合，增強了神經網絡的表達能力。假設特征通道數為16，卷積核的大小為3×3，則該卷積核的特征通道數為16×放大倍數的2次方。

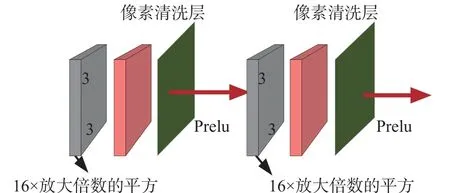
圖5 子像素卷積網絡結構圖

由于像素的擴展方式由其對應的卷積決定，而卷積的參數是通過學習得到的，所以子像素卷積這種基于學習的圖像上采樣方法較傳統放大方法（雙線性插值、雙三次插值等）可以更好地擬合像素之間的關系，從而得到更高質量的初始重建圖像。

2.3 殘差網絡

訓練網絡模型的數據集中常存在冗余信息導致降低了神經網絡學習圖像特征的效果，且隨著網絡深度的增加，訓練產生的錯誤也逐漸累積，冗余的網絡層因學習了非恒等映射參數而導致模型退化，為解決此問題本文引入了殘差網絡。

傳統的殘差結構包含直線向下的殘差映射方式和弧線向下的捷徑連接映射方式。前一種可以學習給定輸入與期望輸出之間的殘差，后一種則能確保殘差網絡中的每個卷積層都有一條將自己的輸出直接傳給較前卷積層的短連接并通過前向傳播特征實現恒等映射，恒等映射可以保證誤差在反向傳播過程的梯度信息不受影響地通過捷徑連接傳向淺層并達到緩解梯度消失現象的效果。該捷徑連接映射方式還可提高神經網絡提取目的特征的能力，促進網絡模型的優化和訓練。

用x表示給定的輸入參數，H(x)表示底層映射的期望輸出，文獻[25]中使用幾個卷積運算來擬合H(·)并 且期望H(·)是一個恒等映射。然而現實中很難直接把H(·)優 化為恒等映射，給定輸入x與期望輸出H(x)之 間會產生殘差F(x)，即：

若H(x)與x近 似相等則殘差F(x)將趨于0，由于卷積層的權值常被零初始化所以容易通過訓練卷積層來實現讓等式(15)中的殘差F(x)趨于0并得到恒等映射的輸出H(x)。

本文的殘差網絡是由四個結構相同的殘差塊組成，每個殘差塊包含兩個卷積和一個跳連接，如圖6所示。其中，卷積核的大小為3×3，每個卷積核有16個特征通道，卷積層后跟有批處理歸一化層[26]和激活函數PReLU層，批處理歸一化可以增強響應大的元素同時抑制響應小的元素，有效提升了模型的泛化性，殘差網絡中的激活函數為網絡模型引入的非線性特性不僅增強了神經網絡的表達能力，還提高了網絡模型的精度，使重建質量得到進一步提升。

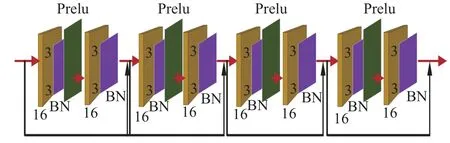
圖6 殘差網絡結構圖

殘差網絡進一步縮小了初始重建圖像與原圖像xi之間的誤差，可以通過方程(21)求出它們之間的殘差估計值：

將初始重建圖像與從殘差網絡得到的殘差估計值相融合，得到經過殘差網絡改善后的重建圖像x*i，該過程如等式(17)所示。本文所提的基于深度學習的壓縮感知自然圖像重建方法中引入殘差網絡使得模型退化和梯度消失問題得到有效解決，并提升圖像的重建精度。

3 實驗結果與分析

3.1 實驗設置

本節用峰值信噪比（PSNR）和結構相似性（SSIM）來評估本文所提算法的性能，分別比較了壓縮感知理論的典型重建算法和基于卷積神經網絡的壓縮感知重建方法，它們的仿真實驗均在Windows 10系統下的python3.6中實現，建模采用版本為torch1.4.0的Pytorch深度學習框架，并利用CuDNN進行加速。實驗中設置：學習率為0.000 1，批歸一化大小為 128，迭代輪數為400。

模型訓練使用COCO2014數據集中的train2014（7 007張圖片）和val2014（3 504張圖片），利用這10 511張圖像隨機裁剪成64×64的子圖像來訓練網絡模型，測試集使用了數據集Set5(5張圖片)和Set14( 14張圖片)[27-28]。

3.2 仿真與分析

3.2.1 與傳統壓縮感知重建算法比較

如圖7、圖8所示，在采樣率為0.25的情況下將本文所提算法（Pro）與文獻[20]的正交匹配追蹤算法（OMP）和文獻[9]的分塊壓縮感知算法（BCS）分別對set14中的man和bridge進行圖像重建，從圖中觀察到基于迭代的正交匹配追蹤算法和分塊壓縮感知算法在采樣率為0.25時SSIM的值很低，圖像細節不清晰甚至損失，而本文所提算法在PSNR、SSIM和視覺效果這三方面要明顯優于壓縮感知理論的傳統圖像重建算法，并且其PSNR值較正交匹配追蹤算法和分塊壓縮感知算法高出17.6 dB 和11.28 dB，值得注意的是，由于傳統壓縮感知圖像重建算法屬于迭代運算其重建過程耗時，本文所提算法重建一張圖像僅需要幾秒并且在低采樣率下有著較高的圖像重建精度。

圖7 在采樣率為0.25時，對Set14man圖像重建性能比較

圖8 在采樣率為0.25時，對Set14bridge圖像重建性能比較

3.2.2 與傳統卷積神經網絡重建算法比較

為了比較使用卷積網絡獲得自適應測量向量的優勢，與文獻[15]中使用插值方式獲得隨機測量向量的超分辨率圖像重建算法（SRResnet）以及Pro_bili和Pro _bicu做比較，其中，Pro_bili和Pro_bicu分別為去掉圖3網絡結構中的最大池化層并保持其他結構和參數不變的情況下利用雙線性插值和雙三次插值來獲得隨機測量向量的算法。如圖9、圖10所示，在采樣率為0.25和0.062 5的情況下將本文所提算法（Pro）、超分辨率圖像重建算法（SRResnet）、Pro _bili和Pro _bicu對Set5中的woman進行圖像重建。上述算法中只有 Pro是使用最大池化層自適應獲得測量向量，其他均使用插值方式獲得隨機測量向量，通過仿真數據和圖像重建質量的對比可以看出Pro的SSIM值在低采樣率下有明顯的優勢，其PSNR比SRResnet、Pro _bili和Pro _bicu 高出1.78～4.72 dB，這是由于最大池化層的輸出是局部接受域中的最大值，這能更有效地保留圖像的紋理特征從而重建出更高質量的圖像，實驗結果表明在低測量率下本文所提算法自適應獲得的測量向量能保留圖像更多主要信息從而有效提升圖像的重建質量。

圖9 在采樣率為0.25時，對Set5woman圖像重建性能比較

圖10 在采樣率為0.062 5時，對Set5woman圖像重建性能比較

為了驗證初始重建階段使用子像素卷積的優勢，將本文算法與初始重建階段使用反卷積網絡的全卷積重建算法做比較。如圖11、圖12所示，在采樣率為0.25和0.062 5的情況下使用本文所提算法（Pro）與文獻[2]的全卷積重建算法（Fully_Conv）和Pro _nor*分別對Set14中的foreman進行圖像重建，其中：Pro _nor*為去掉圖3模型結構中的殘差網絡并保持其它結構參數不變的方法，它是為了驗證最后重建階段使用深度殘差網絡的優勢。在不同采樣率下三種重建算法的SSIM結果相差不大，Pro的PSNR值比Fully_Conv高出2.36～2.38 dB，它們的實驗結果反映出本文所提算法使用子像素卷積進行初始重建的重建性能優于使用反卷積進行初始重建的Fully_Conv，這是由于子像素卷積通過像素清洗層將輸入圖像的像素重新排列實現對圖像的上采樣運算，相較于反卷積它有更高的計算性能，所以基于學習的子像素卷積能得到更高質量的重建圖像。Pro _nor*和Pro的實驗結果展示出殘差網絡對圖像重建精度的影響，在不同采樣率下含有殘差網絡的PSNR值比不含殘差網絡高1.57～2.74 dB，這是由于引入的殘差網絡能進一步縮小初始重建圖像與原圖像之間的誤差從而有效提升圖像的重建精度，該實驗結果驗證了在重構階段引入殘差網絡的優勢。

圖11 在采樣率為 0.25時，對Set14foreman圖像重建性能比較

圖12 在采樣率為0.062 5時，對Set14foreman圖像重建性能比較

3.3 整體對比

本節使用六種重建算法SRResnet、Pro _bili 、Pro _nor*、Pro _bicu、Fully_Conv和Pro對六張圖片man、bridge、foreman、woman、zebra和butterfly進行重建并對比它們的PSNR和SSIM值。表1和表2中黑色加粗數據是本文所提算法的PSNR、SSIM結果，紅色加粗數據是其他重建算法重建六張圖片的PSNR和SSIM的平均值。在采樣率為0.25和0.062 5的情況下本文所提算法達到了最高的平均PSNR和SSIM，它的平均PSNR值分別高出其他方法1.58～4.56 dB和 1.86～3.55 dB，這表明在低采樣率下本文所提算法具有更高的重建精度。

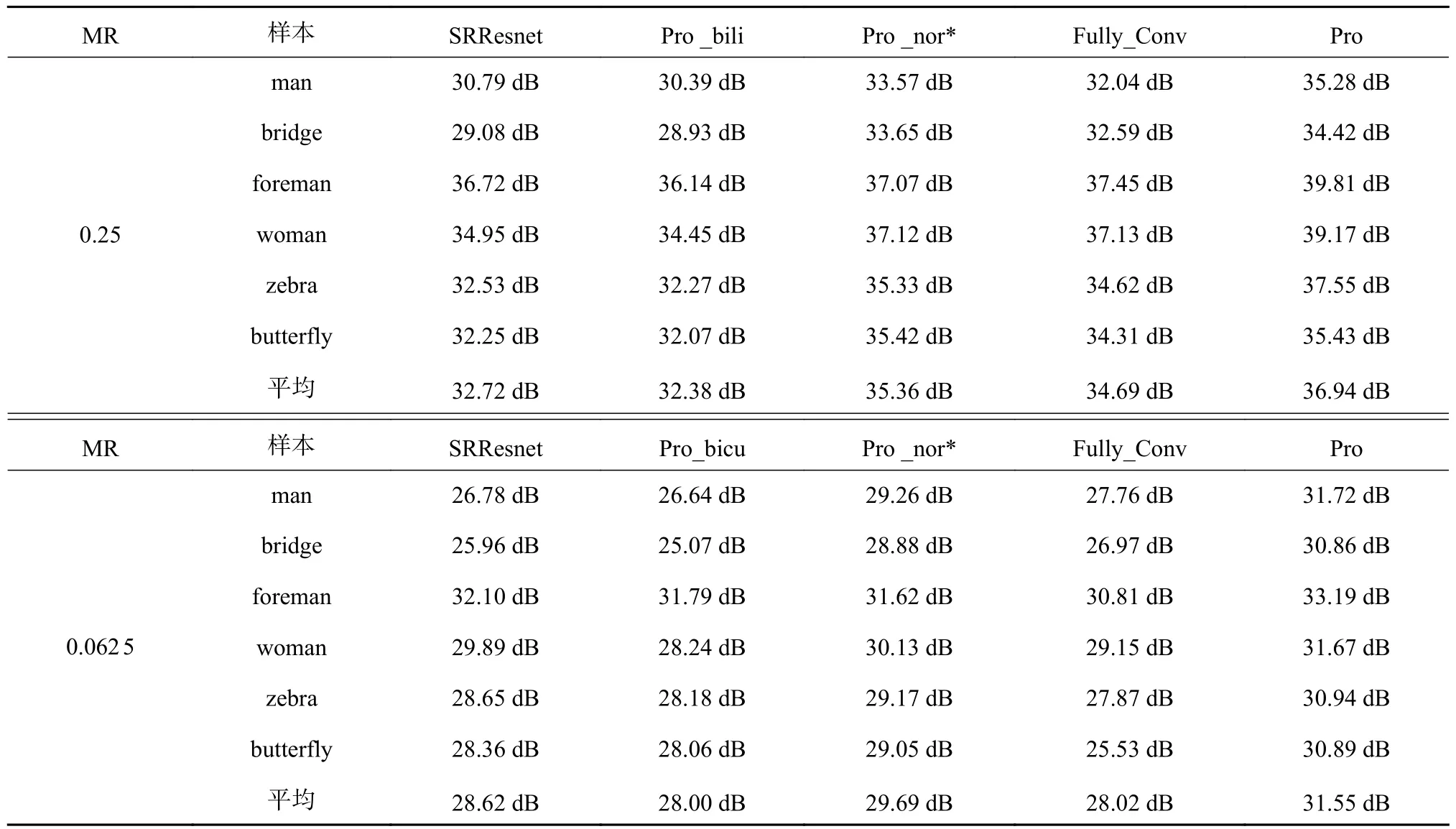
表1 采樣率為0.25和0.062 5時的PSNR結果

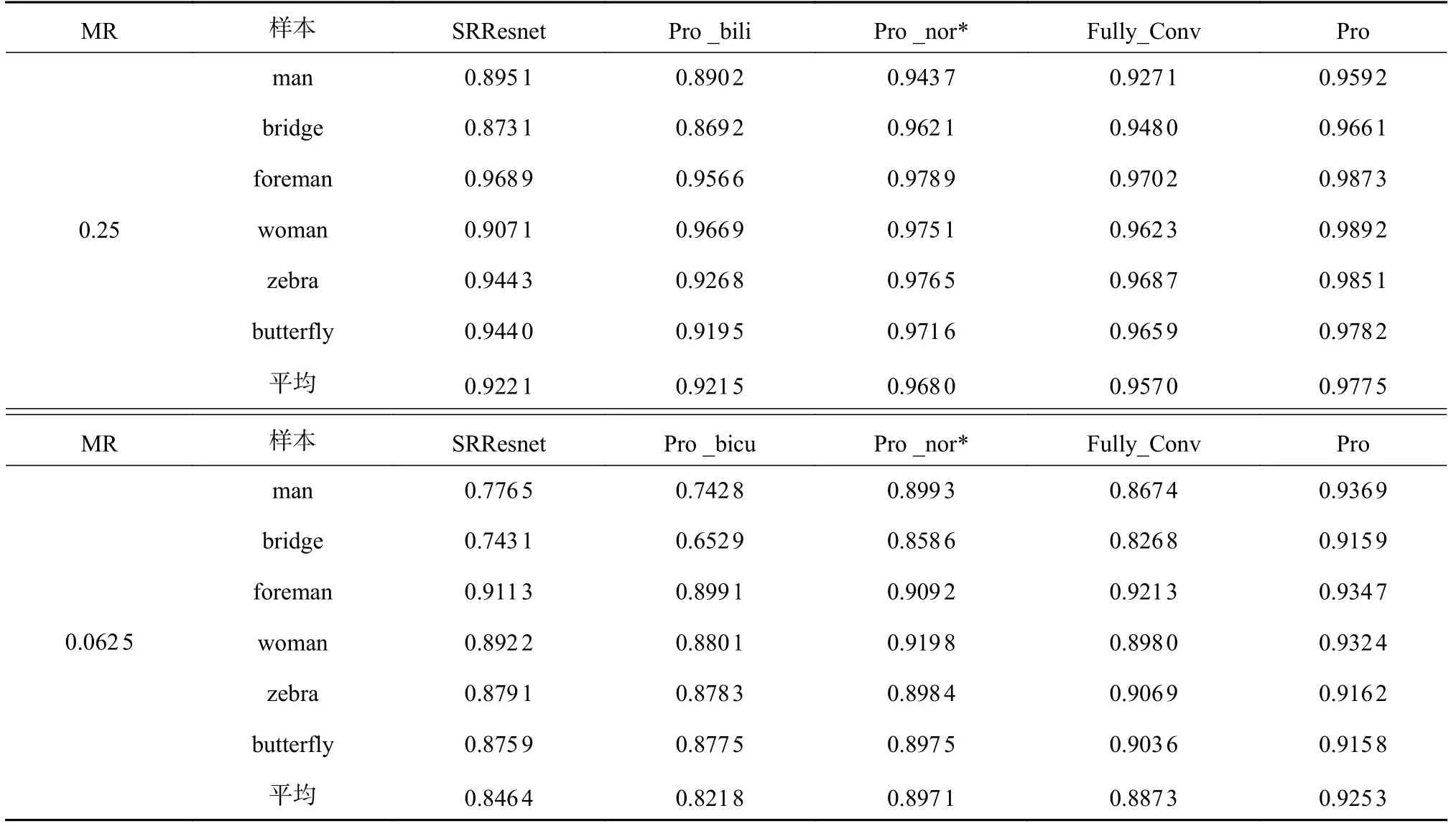
表2 采樣率為0.25和0.062 5時的SSIM結果

4 結束語

針對傳統壓縮感知圖像重建算法存在的運算量大和重建精度低等問題，本文提出了一種基于改進CNN的壓縮感知自然圖像重建方法，該方法首先利用卷積網絡自適應獲得測量向量，其次，將保留了原圖像更多有用信息的自適應測量結果輸入到子像素卷積網絡中來初始重建圖像，由于子像素卷積可有效避免引入過多人工因素，能較好地整合像素之間的關系，從而得到更高質量的初始重建圖像。最后，利用深度殘差網絡進一步縮小初始重建圖像與原圖像之間的殘差，實現了對重建圖像的高精度重建。對比OMP、BCS、SRResnet、Pro _bili 、Pro _nor*、Pro _bicu和Fully_Conv的實驗結果表明本文所提算法在低采樣率下的PSNR和SSIM結果都明顯高出其他方法且隨著采樣率的增大其優勢更加明顯，在采樣率為0.062 5時它的PSNR和SSIM的平均結果分別為31.55 dB和0.925 3。