EMD與改進SVD聯合的脈沖渦流檢測信號降噪方法

宋守許， 汪志全， 蔚 辰， 李 想

(合肥工業大學機械工程學院，安徽 合肥 230009)

0 引 言

軋輥表面質量是其主動再制造時機識別的重要依據。軋制過程中，在復雜的熱/力載荷下，軋輥表面出現疲勞裂紋，影響軋輥的剩余壽命。脈沖渦流檢測技術（pulsed eddy current, PEC）是近幾十年發展起來的電磁檢測技術，其非接觸式檢測的特點可以滿足軋輥表面裂紋在線監測的要求。

由于非接觸式檢測的特點，檢測信號十分微弱，另檢測系統的固有噪聲和工業環境噪聲信號也會混雜在檢測信號中，噪聲信號的存在提高了缺陷信息提取的難度。為了從背景噪聲中提取有效信號，信號降噪成為了至關重要的環節。Yang等[1]提出基于匹配追蹤的小波包分解估計脈沖渦流檢測信號的噪聲強度，并基于最小均方誤差的加權數據融合算法得到特征量的最優估計，抑制了噪聲對特征量的影響。楊理踐等[2]研究發現使用db3小波對脈沖渦流檢測信號進行5層小波軟閾值分解重構能夠達到較好的降噪效果；張智君等[3]提出一種基于自相關函數和方差的改進EEMD降噪方法，并與傳統剔除高噪聲IMF法和EMD閾值降噪方法作對比，結果表明該方法相比原有兩種方法有一定的提升；徐志遠等[4]提出基于維納濾波和主成分分析的脈沖渦流檢測信號降噪方法，用于鐵磁性材料脈沖渦流檢測信號的降噪，實驗結果表明該方法能有效抑制強噪聲對檢測信號的干擾，提高信噪比。

脈沖渦流檢測信號是典型的非平穩信號，其噪聲主要為高頻噪聲。針對非平穩信號的降噪方法主要有中值濾波、低通濾波、小波閾值降噪、EMD降噪等[5-8]。其中中值濾波、低通濾波是基于時域或頻域的算法，會造成信號局部信息的缺失。林忠海等人在寬量程光電傳感器 I-U 特性測試系統中通過仿真實驗的方式選定小波基函數和分解層數在保證信號不失真的前提下提高了信噪比[9]。但小波閾值降噪方法的小波基及閾值選取會影響其降噪性能，其最優閾值的選擇方法問題近年來一直困擾著許多研究人員，而這個問題也成為該方法應用上的瑕疵[10]。EMD降噪方法能夠避免小波基選取問題，但其濾除噪聲時，采用剔除高頻分量或者采用閾值降噪的方式，會存在丟失高頻信息或閾值確定問題[11]。

綜上可知，EMD降噪是一種很好的非平穩信號降噪方法，能夠自適應地將非平穩信號平穩化，但需要進行對其濾除噪聲方式進行改進。考慮到SVD降噪非常適合平穩信號的高頻噪聲濾除，本文提出一種EMD與改進SVD聯合的脈沖渦流檢測信號自適應降噪方法。該方法能夠有效抑制噪聲的干擾，且具有自適應性。

1 基本原理

1.1 經驗模態分解

經驗模態分解(EMD)能夠自適應地將非線性、非平穩信號x(t)分解成一系列的固有模態函數（intrinsic mode function, IMF）和殘余分量（rn）。其中每個IMF是一個窄帶平穩信號，能夠反映信號的局部特征。分解步驟為[12]：

1）找到信號x(t)的所有局部極大值點，并擬合得到上包絡線eU(t)，用同樣的方法得到下包絡線eL(t)。根據上下包絡線，求出信號的局部平均值

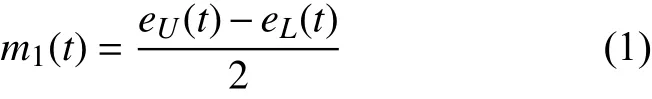
2）求原信號與局部平均值的差

3）通常，h1（t）不滿足IMF的條件。用h1(t)代替信號x(t)，重復（1）、（2）k次，得到h1k(t)=h1(k–1)(t) –m1k(t)，使得h1k(t)滿足IMF的條件，令c1(t)=h1k(t),則c1(t)即為第一階IMF。

4）將信號x(t)去除高頻分量c1(t)后得到的新信號r1(t)取代x(t)，重復（1）、（2）、（3），得到一系列的IMF，直至殘余分量rn(t)為單調函數。此時，EMD分解結束，原信號表示為：

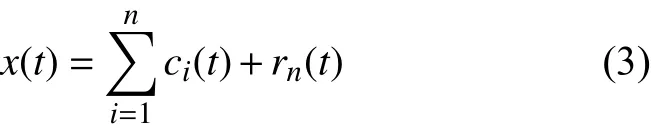
式中：c1(t)～cn(t)——信號x(t)從高到低不同頻段的信息；

rn(t)——信號的直流分量或平均趨勢項。

一般認為噪聲主要分布在前幾階高頻IMF，直接舍去這些IMF，利用其余IMF重構信號即可達到降噪的目的。

1.2 奇異值分解降噪原理

奇異值分解（singular value decomposition, SVD）降噪對含噪平穩信號構造的矩陣進行分解，基于噪聲和信號的能量可分性，僅保留信號特征值，達到去除噪聲的目的[13]。根據Hankel矩陣形式，可以將信號c(t)構造成一個m×n的信號實矩陣，其形式如下:

其中N為信號長度，1＜n＜N，m=N–n+1。

對于實矩陣Hm×n，必存在酉矩陣Um×m和酉矩陣Vn×n，使得如下公式成立：

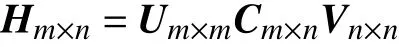
其中Cm×n為m×n階實對角陣，可以表達成：

式中，Σ=diag(σ1, σ2,σ3, ···, σr), σ1＞σ2＞σ3＞ ···＞σr＞0，σi為Hm×n的奇異值。前k個奇異值較大，包含了矩陣Hm×n的大部分信息，將代表噪聲的較小奇異值置零，然后進行SVD逆運算過程得到重構信號，完成信號降噪。由此可見，有效秩階數k的選取方法對SVD降噪性能有很大影響。

1.3 降噪性能評價指標

在研究不同降噪方法的性能時，可首先通過對其降噪信號的波形特點進行定性分析，然后還需對性能定量分析。以信噪比和均方誤差為指標可以有效定量評估降噪性能。信噪比SNR和均方誤差Rmse的定義分別為：

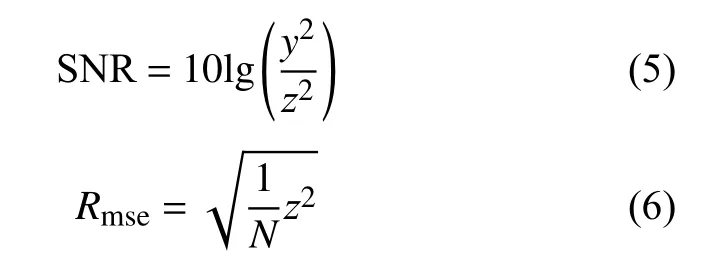
式中：N——信號長度；

y——純信號；

z——純噪聲。

對于實測信號，y、z均無法獲知，故采用估計的方法。以降噪后的信號代替純信號y，以原始信號s與y的 差值代替純噪聲信號，即z=s–。原始信號與降噪后信號的信噪比越大，均方誤差越小，則降噪后的信號越接近真實信號，降噪的效果越好。

2 EMD-改進SVD聯合降噪方法

2.1 改進SVD降噪方法

關于有效秩階數k的確定，目前并沒有統一的方法，常用的差分譜方法降噪結果并不理想，容易出現過降噪的現象[13]。信噪比是評價降噪方法性能最常用的指標，但是對于實測信號，降噪信號的信噪比不能直接計算，可采用1.3節方法進行估計。本文提出一種基于估計信噪比曲線的有效秩階數確定方法。

研究表明，平穩信號經SVD分解得到的奇異值的大小取決于對應頻率成分的幅值[14]。構造不同幅值頻率成分的平穩仿真信號x(t)，其表達式為：

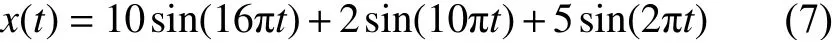
x(t)由3個不同頻率成分構成，分別為8 Hz、5 Hz、1 Hz，對應的幅值分別為10、2、5，信號長度取1 024。使用awgn函數添加信噪比為3 dB的白噪聲，得到加噪信號x1(t)。

選擇不同的有效秩階數對加噪信號進行降噪，根據式（5）可以得到降噪后信號的估計信噪比和實際信噪比曲線如圖1所示。由圖1(a)可以發現，當有效秩階數k的數值增大時，降噪信號的信噪比先增大后減小。信噪比峰值點對應的有效秩階數為最佳有效秩階數，此時，降噪效果最好；圖1(b)所示估計信噪比曲線可分為三段：第一段隨著代表有用信號奇異值個數的增加，估計信噪比曲線快速上升；第二段隨著代表噪聲信號奇異值個數增加，估計信噪比曲線上升速率減緩；第三段當選取奇異值個數接近最大值時，信噪比曲線極速上升。其中圖1(b)中第一個拐點對應的橫坐標與圖1(a)中峰值點對應的橫坐標相近。相比于圖1(a)，圖1(b)中后兩段的異常是由于估計得到的噪聲會隨著奇異值個數增加而減小導致的，尤其是當奇異值個數接近最大時，估計得到的噪聲接近于0，所以估計信噪比極速上升。

由上述分析可知，選取圖1(b)中第一個拐點對應的有效秩階數重構降噪信號，能夠達到最佳的降噪效果。選取方法具體步驟如下：

圖1 有效秩階數-信噪比曲線

Step1：分別計算取不同有效秩階數k時SVD降噪信號的估計信噪比SNR（k），k取偶數；

Step2：計算得到有效秩階數-估計信噪比差分曲線

Step3：計算m的中位數m0.5，并以中位數為閾值，確定有效秩階數k1

2.2 EMD-改進SVD聯合降噪方法

研究發現，直接舍去前幾階高頻IMF的EMD降噪方法存在嚴重不足[15]：高階IMF中不僅含有噪聲，可能也會含有一定的有用信號。當背景噪聲較大時，該方法降噪效果不好，甚至完全失效。EMD閾值降噪方法的降噪效果受閾值選取方法影響較大，降噪效果的穩定性較差因此，本文結合EMD自適應性分解和SVD善于去除平穩信號高頻噪聲的特點，提出一種聯合改進SVD的EMD降噪方法。首先將非平穩信號經EMD分解成若干個平穩的IMF，然后采用改進SVD將平穩IMF中的高頻噪聲濾除后重構信號。該方法的流程如圖2所示。

圖2 EMD-改進SVD聯合降噪方法流程圖

對應的實現步驟為：

Step1：根據IMF與原信號相關系數，區分噪聲主導分量和信號主導分量，噪聲主要分布在前幾階高頻IMF。

Step2：以相關系數第一個局部極值點為分界點K，IMF1～IMFK為噪聲主導分量，IMFK+1～IMFn

為信號主導分量。相關系數R(x,ci)的定義為

Step3 ：采用改進SVD降噪方法對IMF1～IMFK進行降噪，提取其中的微弱信號。降噪后的IMF分量為IMF1′～IMFK′。

Step4：以信號主導分量和降噪后的噪聲主導分量重構信號，得到降噪信號：

3 仿真信號降噪分析

為驗證所提降噪方法的有效性和優越性，基于Matlab軟件，利用仿真信號對所提方法進行分析。

3.1 改進SVD降噪方法性能研究

EMD分解得到的IMF分量是窄帶平穩信號，故采用平穩仿真信號對改進SVD降噪方法進行研究，仍選擇2.1節的仿真信號x(t)及其加噪信號x1(t)。圖3為仿真信號和加噪信號的時域圖。分別運用奇異值差分譜和改進SVD降噪方法對加噪信號進行降噪處理，得到降噪信號時域圖如圖4所示。對比圖3、圖4可以看出，SVD差分譜與改進SVD均有效消除了部分噪聲，但改進SVD得到的降噪信號時域圖與仿真信號時域圖波形更接近，降噪效果更好。

圖3 仿真信號與加噪信號時域圖

圖4 兩種方法降噪信號時域圖

為研究不同初始信噪比下的降噪性能，向仿真信號中分別添加–3 dB、0 dB、3 dB、6 dB、12 dB的白噪聲，以信噪比為評價指標，對降噪性能進行評價，得到圖5所示不同初始信噪比下降噪性能對比結果。

從圖5可以看出，在一定初始信噪比范圍內，改進SVD降噪方法降噪性能明顯優于SVD差分譜降噪方法：當初始信噪比為-3 dB時，改進SVD與SVD差分譜方法的信噪比增量分別為12.55 dB、12.30 dB；當初始信噪比為12 dB時，改進SVD與SVD差分譜方法的信噪比增量分別為19.73 dB、3.15 dB。即當初始信噪比較高時，改進SVD降噪方法的優勢更加明顯。

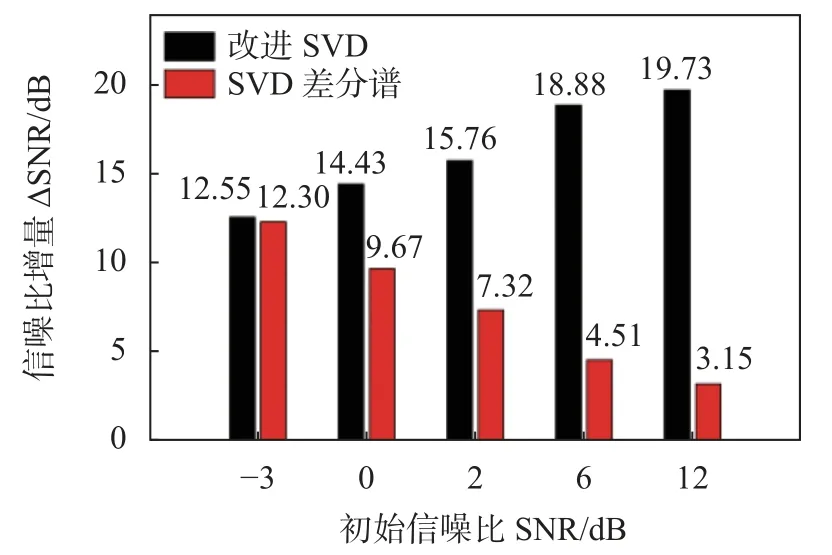
圖5 不同初始信噪比下降噪性能

3.2 EMD-改進SVD聯合降噪方法性能研究

為驗證聯合降噪方法有效性和優越性，以圖6(a) 所示heavy sine標準測試信號模擬脈沖渦流檢測信號進行實驗，信號長度為1 024。一般認為脈沖渦流檢測信號噪聲為高頻噪聲[12]，可以近似看做白噪聲。在上述測試信號中疊加12 dB的白噪聲，分別采用EMD軟閾值降噪、5層小波軟閾值降噪和EMD-改進SVD聯合降噪方法進行降噪處理。降噪結果如圖7所示，與圖6(b)所示加噪信號對比可知，各降噪方法對噪聲均有一定的抑制作用。但是，EMD閾值降噪信號的波形平滑性較差，小波降噪信號的波形平滑度較好，但是都存在一些突變點，這對信號特征分析的干擾很大，EMD-改進SVD聯合降噪信號的波形的平滑性較好，同時沒有突變點的問題，能夠很好表現原信號的特征。

圖6 heavy sine信號與加噪信號時域圖

圖7 heavy sine信號降噪時域圖

為定量評價各方法的降噪性能，以信噪比SNR和均方誤差Rmse為指標，計算結果如表1所示。

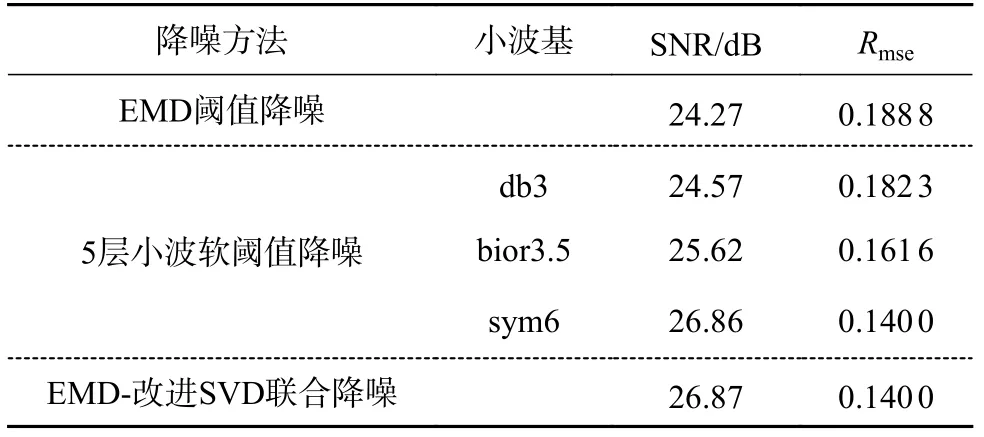
表1 3種方法降噪性能比較

從表1可以看出，信號經過EMD-改進SVD聯合降噪的SNR最大，為26.87 dB，Rmse最小，為0.140 0，故而降噪效果最好。相比于EMD閾值降噪信號的SNR、Rmse分別為24.27 dB、0.188 8，改進SVD的降噪性能有明顯提升；小波軟閾值降噪方法中，sym6小波軟閾值降噪性能最好，其SNR、Rmse分別為26.86 dB、0.140 0。與之相比，EMD-改進SVD聯合降噪方法的性能提升較小，但是避免了小波基選擇問題，具有自適應性。

綜合上述分析，改進SVD降噪方法可以有效濾除平穩信號中的高頻噪聲，結合EMD，能夠對非平穩信號中的高頻噪聲進行濾除，其降噪性能與自適應性較小波閾值降噪和EMD閾值降噪都有一定提升。

4 實測信號降噪分析

本文實驗研究的背景是基于脈沖渦流檢測信號的高速鋼軋輥表面缺陷識別，試件為預制長度為6.0 mm，深度為1.5 mm，寬度分別為0.5 mm、1.5 mm、2.5 mm矩形缺陷的高速鋼平板。

激勵信號電壓為5V、周期為100 Hz，以1 MHz采樣頻率采集數據。選取一個周期信號進行后續降噪處理，圖8為缺陷寬度0.5 mm時的檢測信號。

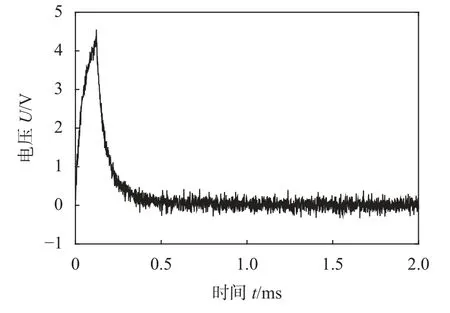
圖8 缺陷寬度0.5 mm的檢測信號

分別使用EMD閾值降噪、EMD-改進SVD聯合降噪和降噪效果最優的5層sym6小波軟閾值降噪，得到的降噪信號如圖9所示，三種方法均能在一定程度上消除噪聲的影響，但EMD-改進SVD聯合降噪得到的信號更加平滑，符合脈沖渦流檢測信號的特點。各方法降噪信號的信噪比和均方根誤差如表2所示，與表1對比可知，實測信號降噪結果與仿真信號降噪結果相吻合。

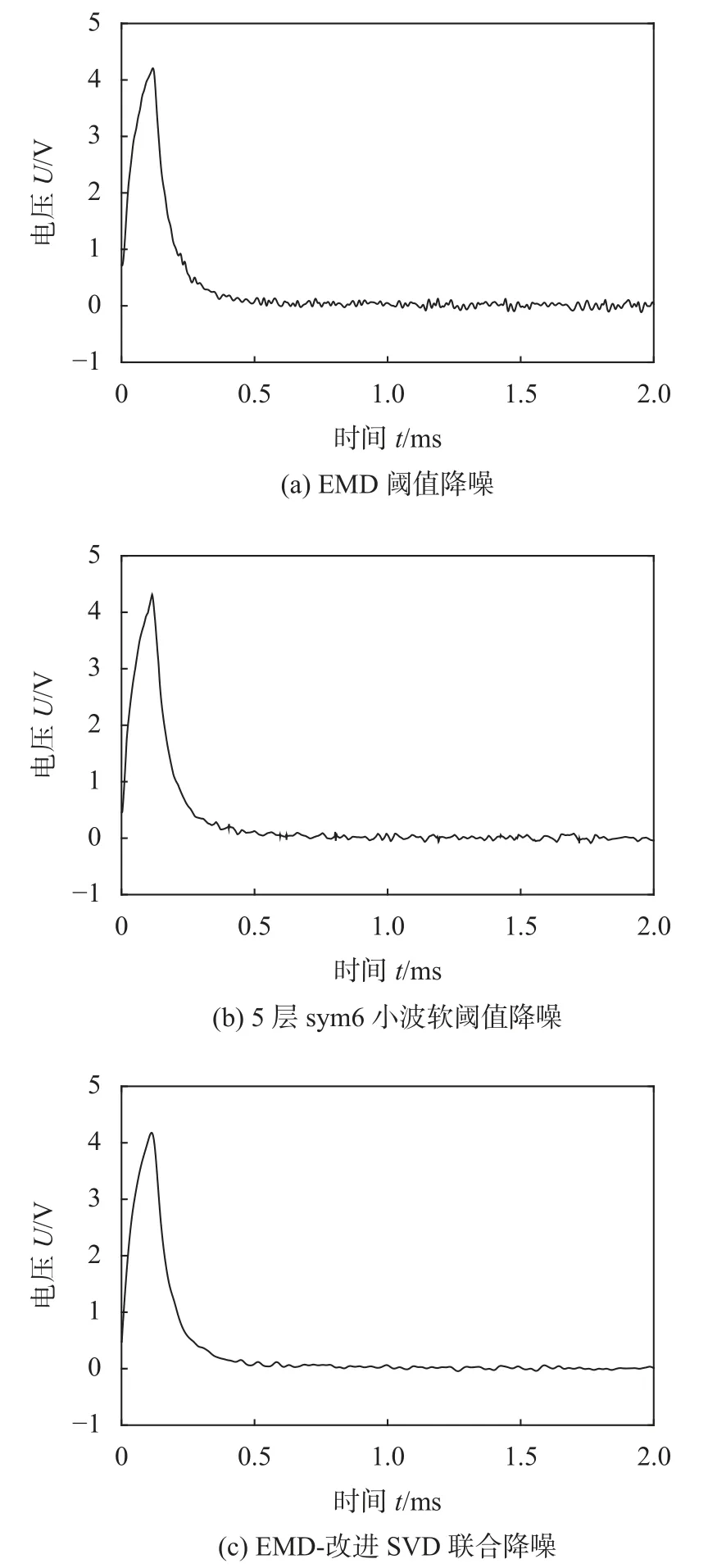
圖9 缺陷寬度0.5 mm的降噪信號

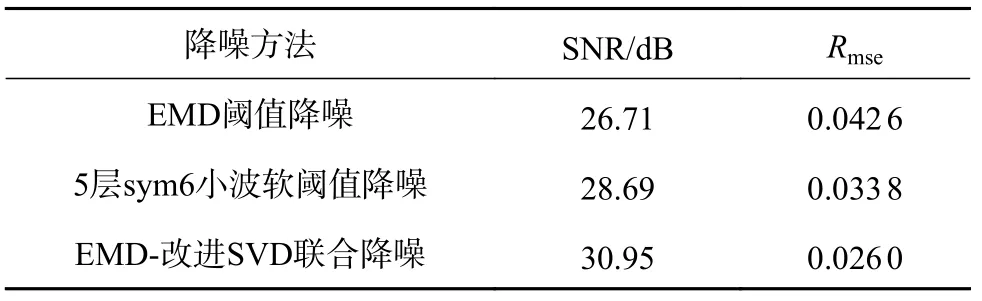
表2 3種方法降噪性能比較

采用EMD-改進SVD聯合降噪方法，分別對不同缺陷寬度的檢測信號進行降噪處理，得到信號如圖10所示。

圖10 不同寬度缺陷的降噪信號

從圖10可以看出，在缺陷寬度較小時，不同寬度缺陷的信號仍然能夠區分：當缺陷寬度增加時，信號峰值減小。

5 結束語

1）提出了一種基于估計信噪比的SVD有效秩階數確定方法，對SVD降噪進行了改進，該方法降噪性能相比于SVD差分譜降噪有明顯提高。

2）提出了EMD與改進SVD聯合的脈沖渦流檢測信號降噪方法，相比于小波閾值降噪和EMD閾值降噪方法，該方法能避免小波基選取和閾值確定問題，同時具有更高的信噪比和更低的均方誤差，經實測信號驗證該方法較其他兩種方法，能將信噪比提高至30.95 dB，其均方誤差降低至0.026 0。

3）通過實測信號的分析驗證，EMD與改進SVD聯合降噪方法能夠提取信號中的有效成分，區分不同寬度缺陷信號的波形，實現缺陷尺寸的識別。