從“算術”到“代數”:字母表示數的魅力
文/葉旭山
和小學數學相比,初中數學與之最大的區別之一就是抽象程度的提高,簡單地說,就是從“算術”跨越到“代數”。小學數學中出現的主要是具體的數,而到了初一,同學們會接觸到更多的字母。這其實是數的概念的發展,是從“算術”到“代數”的過渡。
請大家參與下面這個小游戲,進一步體會“字母表示數”的魅力,感受“算術”和“代數”的主要區別。
游戲規則:(請大家保持測試現場的絕對安靜,按照規則進行測試,不和他人交流)從1—9中選一個你喜歡的數字,乘3,加3,再把得到的數乘3,然后把個位與十位的數字相加,在心里記住這個結果,稍后查看對應數字代表的人物(如表1),就能知道自己的“有緣人”。
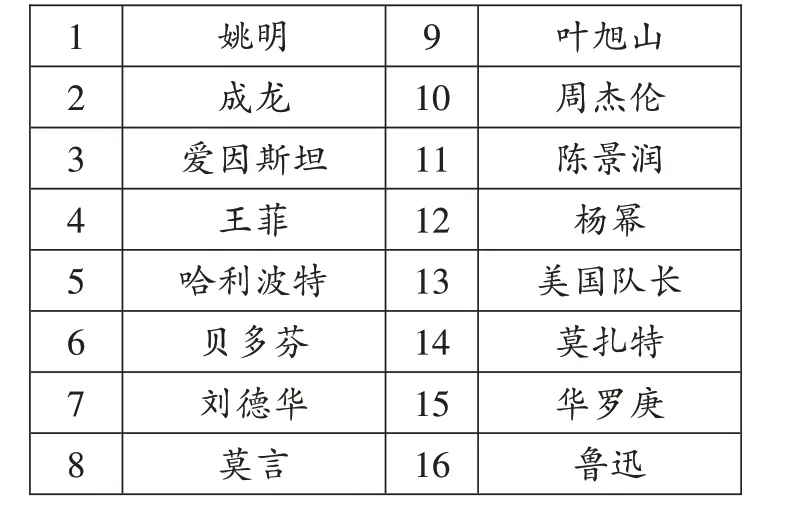
表1
備注:為了拉近與大家的距離,筆者將數字9 對應的人物設置為筆者自己(葉旭山),大家也可以根據具體活動的需要,調整數字對應的人物,進一步體會這個游戲的趣味性。
游戲揭秘:該游戲的最后結果都是一致的(數字9),哈哈,看來大家與我都很有緣。如何解釋這種現象呢?
方法1:把1—9 的9 個數字全部算一遍,發現結果都是9。
方法2:把心里想的那個數字設為a,那么依據規則將這個數字a乘3,加3,再把得到的數乘3,可得3(3a+3)=9a+9=10a+(9-a)。因此十位上的數字是a,個位上的數字是9-a。再依據規則把個位與十位的數字相加,也就是a+(9-a)=9,所以結果都是9。
相信大家參與這個游戲之后,能切實感受“用字母表示數”的必要性和優越性。在游戲揭秘的過程中,方法1 運用完全歸納法,說理很嚴密,但需要計算9次,比較麻煩;方法2本質上屬于嚴格代數推理范疇,是運用字母代替數字,依據運算規則來揭示這個游戲背后的數學本質。同學們在日常的生活和學習中,如果能學會用字母表示數去解釋現象背后的本質,初步形成運用符號表達的意識,發展有序思考的習慣,就一定能夠積累很多數學思維的基本經驗。

