關注數學學習經驗，設計適性的階梯式單元提升作業
——以“全等三角形”單元學習為例

易良斌 浙江省杭州市上城區教育學院 310020

吳維靜 杭州師范大學東城中學 310000

引言

作業是我們日常教學的重要組成部分，其主要目的一方面是為了幫助學生鞏固知識，促其進步；另一方面則是幫助教師反饋教學效果，達到精準教學的目的.數學單元作業是教師在單元目標和單元設計的指導下，將單元內零散、單一的作業采取刪減、增補、重組等方式整合，在單層面統籌考慮整個單元的系列性作業［1］.“雙減”政策明確要求減輕義務教育階段學生的作業負擔，如何在有限的時間里設計更高效的作業，無疑對教師的作業設計水平提出了更高的要求.在此背景下，筆者以“全等三角形”為例，嘗試設計適性的階梯式單元提升作業.

設計思路與核心

筆者發現在幾何題的講解中，學生有時僅僅只差某一個提示就能完成整道難題.而數學作業具有針對性、發展性、探究性、差異性等特征，于是筆者在基于學情的背景下嘗試階梯式單元提升作業設計，它以維果茨基“最近發展區”理論為主要依據，同時結合“支架式教學”“類比教學”“變式訓練”“啟發式問題串”等教學理念的優點進行設計.

本文提到的階梯式單元提升作業即作業沒有明確的分層，但是每一個專題和問題之間都有相關的聯系，難度按照相對較小的階梯進行，因此每題都可能成為不同能力學生的“分水嶺”［2］.教師不會告訴學生問題的難度指數，避免學生產生心理定式，學生將根據自身能力進行選擇，從而在逐步提升自我需求的同時滿足教師要求和學生需求之間的平衡.由于階梯較小，學生能通過問題之間細小的變化得到相關的提示，從而建立完成作業的信心，降低對數學難度的恐懼，逐步完成更高等級的作業，進一步逼近自身的“最近發展區”.

本作業設計充分關注學生已有的數學經驗，從學生的高頻錯題出發，根據錯因分析針對學生的薄弱點設計階梯式作業，秉承從易至難、從基礎知識到應用能力的梯度設計4個課時模塊（圖1），從而更好地體現單元提升作業中的提升性、反思性、應用性和拓展性要求.

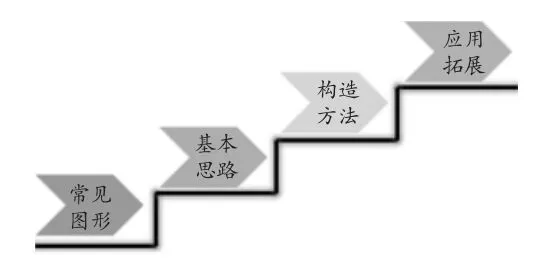
圖1 單元設計模塊

其中將每課時的作業量控制在6題以內，設計以下四種類型的作業（圖2），以“習題演練，自我提升—歸納總結，自我反思—綜合應用，自我鞏固—拓展創新，自我突破”設計4個主題模塊，其中提升型作業注重相關考點、題型的演練，落實“雙基”；反思型作業注重方法歸納總結，滲透數學思想；應用型作業注重綜合應用知識點解決問題，發展關鍵能力；拓展型作業注重思維發散，進一步提升核心素養.

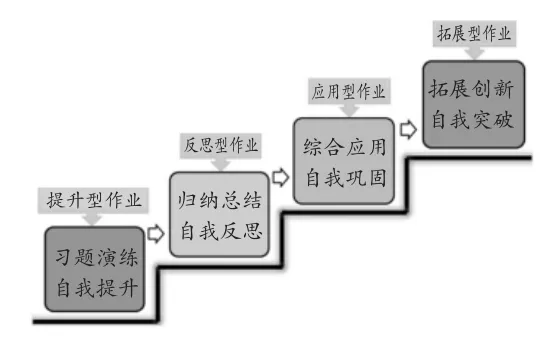
圖2 課時作業設計模塊

通過提升型作業歸納總結得到一定的知識儲備，進而對知識進行應用與發散，最后由交流提煉得到進一步提升.學生通過經歷“提升—反思—應用—拓展”的步驟來自主建構知識框架，從而提高幾何直觀、推理能力、應用意識和創新意識等核心素養，增強邏輯推理能力和邏輯表達能力等關鍵能力.

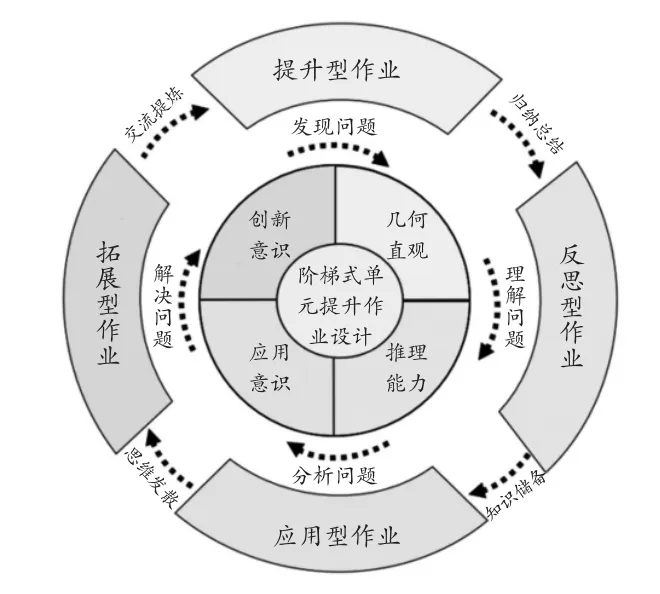
圖3 作業設計與核心素養的關系

單元主題和設計目標

（一）單元主題

“全等三角形”是幾何入門所必需的基礎知識和基本技能，是初中幾何從實驗階段過渡到論證幾何階段的關鍵節點，在培養學生的邏輯推理能力和邏輯表達能力方面具有重要作用.本文為基礎教學完成后進行的提升作業設計，通過學生自主探索三角形全等的條件，歸納常見圖形和基本思路，研究全等三角形的應用價值，從而引導學生深度建構，發展核心素養與關鍵能力，為進一步學習四邊形、圓、相似三角形等其他幾何知識打下良好的基礎.

（二）設計目標

見表1.

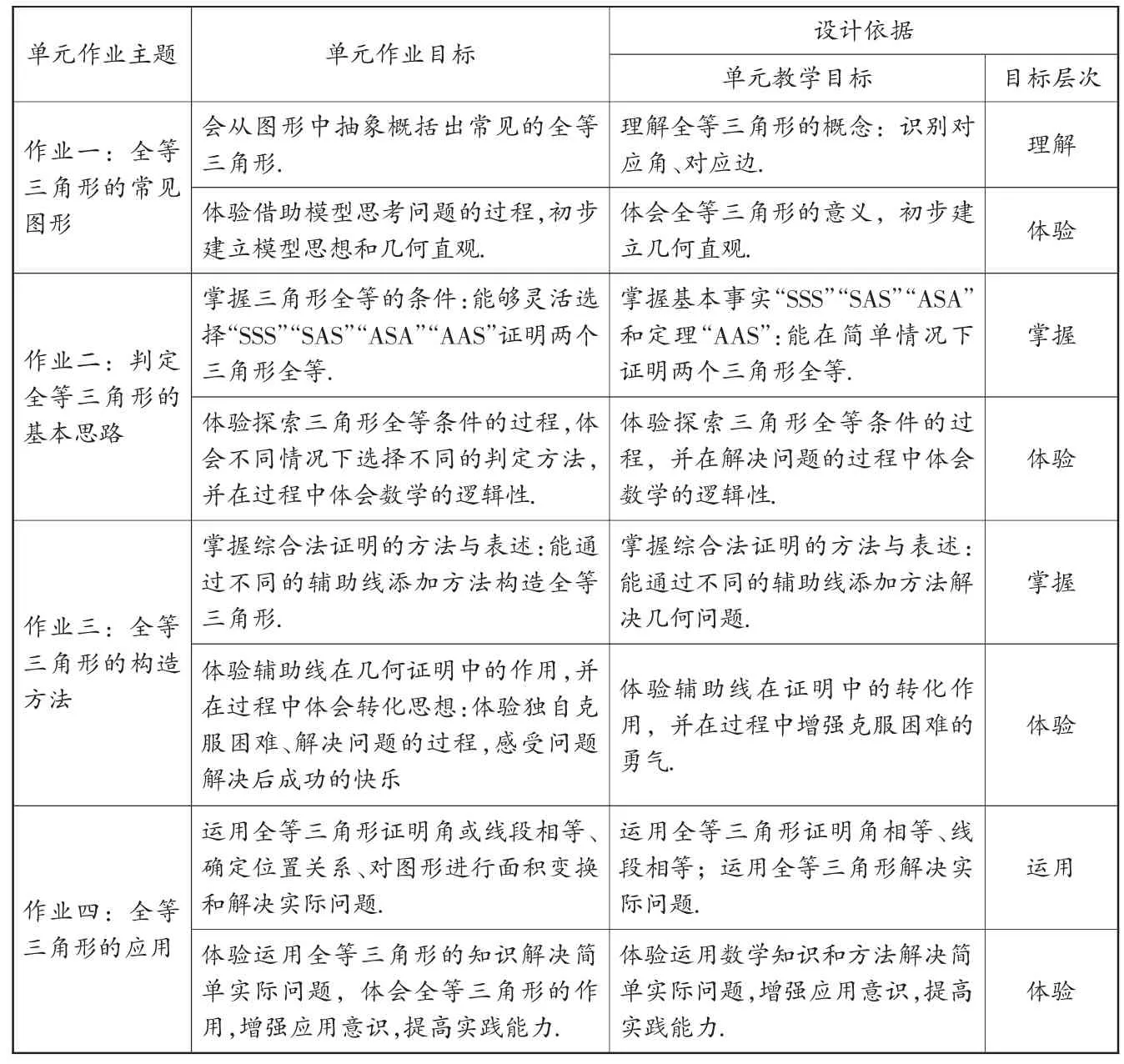
表1 作業設計目標

作業設計分析

以學生的高頻錯題為出發點，通過學生自主完成、歸納總結、思維發散、交流提煉的形式進行，由于篇幅有限，筆者將以作業（三）全等三角形的構造方法以及作業（四）全等三角形的應用為例進行具體分析.

作業（三）全等三角形的構造方法

作業中高頻錯題：

（作業本1.5.1 第6題）如圖4，已知AB=DC，AC=DB，求證：∠A=∠D.

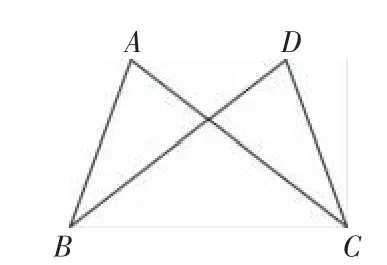
圖4

下面是兩位同學的對話：

方方說：根據條件，找不到全等三角形，圓圓說：如果添加輔助線，就可以找到全等三角形了，請根據提示給出證明.

（作業本1.5.2第7題）如圖5，在△ABC 中，AB=5，AC=9，AD 是BC 邊上的中線，則AD 的取值范圍是（）

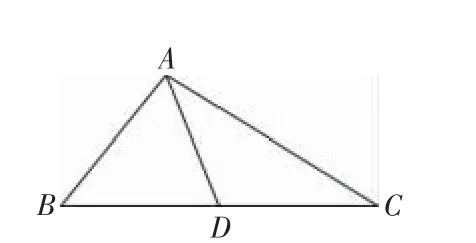
圖5

A.4＜AD＜14 B.0＜AD＜14

C.2＜AD＜7 D.5＜AD＜9

錯因分析上述兩題都需要增添輔助線，對于此類題型，能否添對輔助線構造出合適的全等三角形是解決問題的關鍵，而學生對輔助線的添法往往沒有頭緒.

就此，筆者設計提升作業“全等三角形中常見的構造方法”，借此為學生在解決幾何問題中添加輔助線提供思路.

全等三角形的構造方法

一、習題演練，自我提升

類型1：連接線段

1.如圖6，已知AB=DC，AC=DB，求證：∠B=∠C.

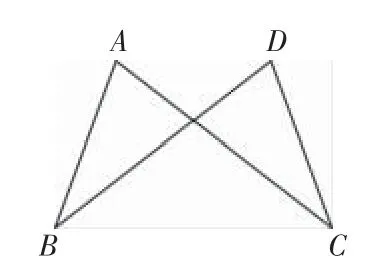
圖6

類型2：作垂線

2.已知：如圖7，DA平分∠CAB，∠ABD+∠ACD=180°，∠B=90°，易證：DB=DC.

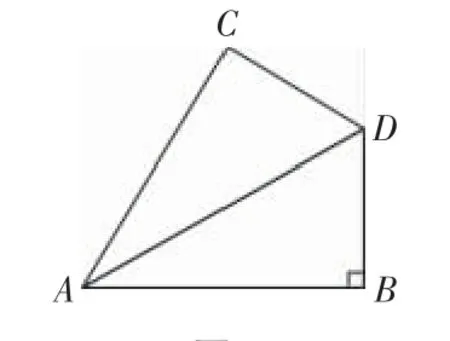
圖7

探究：如圖8，DA平分∠CAB，∠ABD+∠ACD=180°，∠B＜90°，求證：DB=DC.

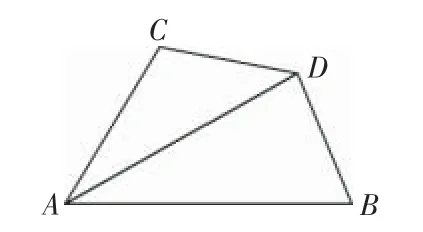
圖8

類型3：倍長中線

3.如圖9，在△ABC中，D為BC的中點，求證：AB+AC＞2AD.

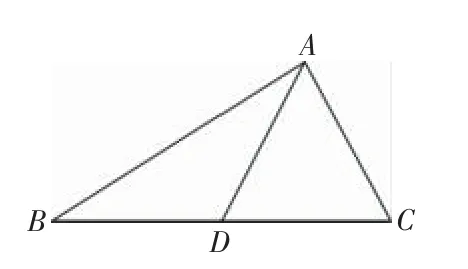
圖9

類型4：截長補短

4.如圖10，AB∥DC，AD⊥CD，點P在AD 上，BP，CP分別平分∠ABC，∠BCD.（1）求證：PA=PD；（2）求證：AB+CD=BC；（3）若去掉AD⊥CD這個條件，上述兩問的結論是否仍成立？

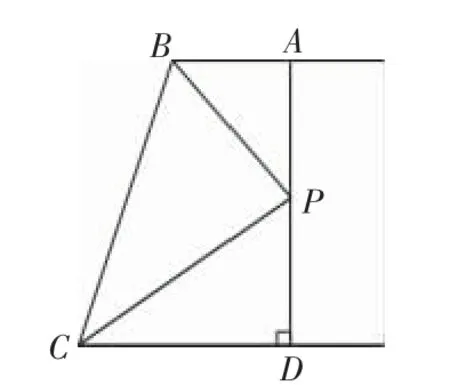
圖10

二、歸納總結，自我反思

根據上述幾種題型的練習，你能否結合平時所學總結常見的構造三角形的方法？請試著歸納出來.

三、綜合應用，自我鞏固

5.如圖11，在△ABC中，∠C=2∠B，DA為∠CAB的角平分線，求證：AB=AC+CD.

圖11

四、拓展創新，自我突破

6.（1）問題解決：請你證明下面命題，如圖12，在△ABC中，D是BC的中點，DE⊥DF且DE與AB相交于點E，DF與AC相交于點F，連接EF，求證：BE+CF＞EF.

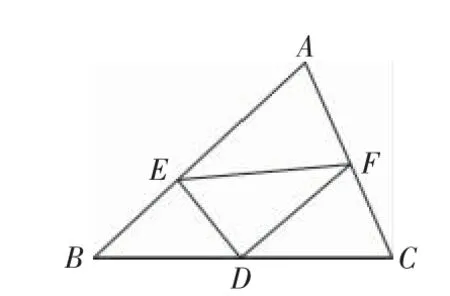
圖12

（2）問題拓展：如圖13，在四邊形ACDB 中，∠ABD+∠ACD=180°，BD=CD，∠CDB=120°，在頂點D處作一個60°的角，角兩邊分別交AB，AC于點E和點F，連接EF，猜想線段EF，BE，CF之間的數量關系，并說明理由.

圖13

設計意圖引導學生感受全等三角形中不同的添加輔助線的方法：連接線段、作垂線、倍長中線、截長補短和旋轉，通過不同的添加輔助線的方法感受輔助線在解決幾何問題中“搭橋牽線”的作用及優越性，及時滲透轉化思想.

另外，在作業講解時教師要對不同背景選擇不同的方法進行總結：若出現角平分線則優先考慮作垂線；若有中線條件優先考慮倍長中線；若猜想兩條線段之和等于第三條線段的證明優先考慮截長補短；有兩邊相等、旋轉后為一條直線的問題時優先考慮通過旋轉來構造全等三角形.同時教師要引導學生理解輔助線的作法往往不唯一，需要我們平時多積累與總結.

作業（四）全等三角形的應用

作業中高頻錯題：

（作業本復習題第12題）已知：如圖14，點B，C，D在同一條直線上，∠ACB=∠ECD=60°，AC=BC，EC=DC.連接BE，AD，分別交AC，CE于點M，N，求證：（1）△ACD≌△BCE，（2）CM=CN.

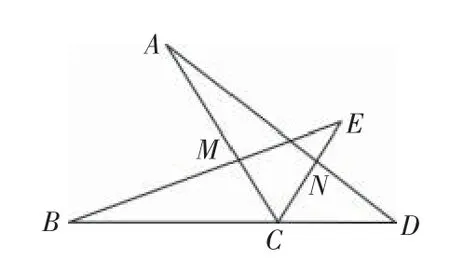
圖14

錯因分析找不到合適的全等三角形，或雖然找到全等三角形，但是認為缺少證明的條件，不理解第一問證出的全等有何用處.

因此筆者設計提升作業“全等三角形的應用”，讓學生體會全等三角形在實際解決問題中的作用.

全等三角形的應用

一、習題演練，自我提升

類型1：證明線段、角相等

1.如圖15，已知AC與BD相交于點O，AB=DC，∠D=∠A.

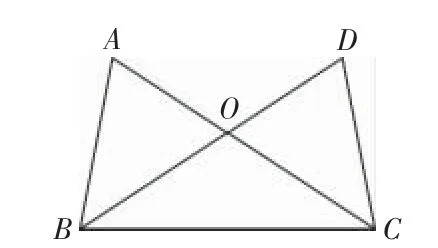
圖15

（1）請寫出你認為正確的5個結論（對頂角除外，且不再添加輔助線）.

（2）從你寫出的結論中，任選一個說明理由.

類型2：證明位置關系

2.兩個等腰直角三角形三角板如圖16①所示放置，將它抽象出圖16②的幾何圖形，其中B，C，E在一條直線上，連接CD.

（1）圖16②有全等三角形嗎？請說明理由；（2）證明：DC⊥BE.

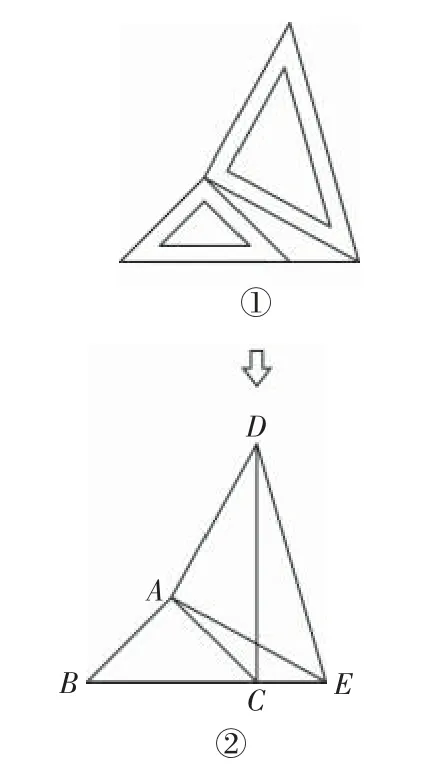
圖16

類型3：進行面積變換

3.如圖17，在四邊形ABCD中，AD=AB，∠BAD=∠BCD=90°，AC=5，則四邊形ABCD的面積是多少？

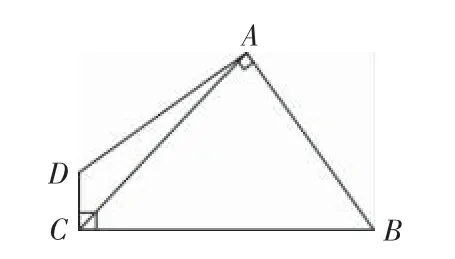
圖17

類型4：解決實際問題

4.如圖18，為了測量湖泊E與岸邊D和A的距離，進行如下操作：

圖18

（1）作線段AB，取其中點O；

（2）連接DO并延長使DO=OC；

（3）連接BC；

（4）連接EO交BC于點F，測量BF，CF的長度即可知道AE和DE的長度，請說明這樣做的理由.

二、歸納總結，自我反思

通過上述練習，你是否已經感受到全等三角形的作用？請你嘗試歸納總結全等三角形常見的應用價值.

三、綜合應用，自我鞏固

5.已知在四邊形ABCD中，AC與BD相交于點E，AC⊥BD，作BF⊥CD交CD于點F，BF與AC交于點G，∠EGB=∠EDA.

（1）如圖19，求證：AD=CD；

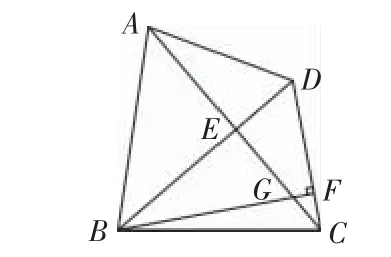
圖19

（2）如圖20，BH是AE上的中線，若DE=EG，AE=2DE，是否有三角形的面積等于△ADE面積的2倍？請直接寫出來.

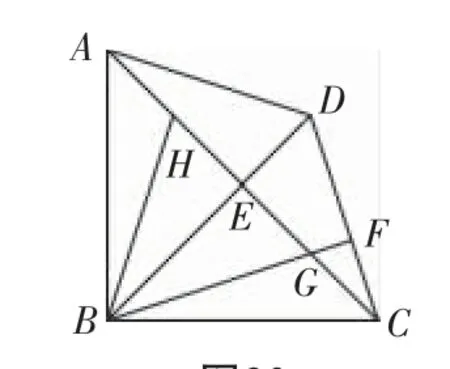
圖20

四、拓展創新，自我突破

6.問題背景：如圖21，在四邊形ABCD 中，AB=AD，∠DAB=120°，∠ABC=∠ADC=90°，E，F分別是BC，CD上的點，且∠FAE=60°.

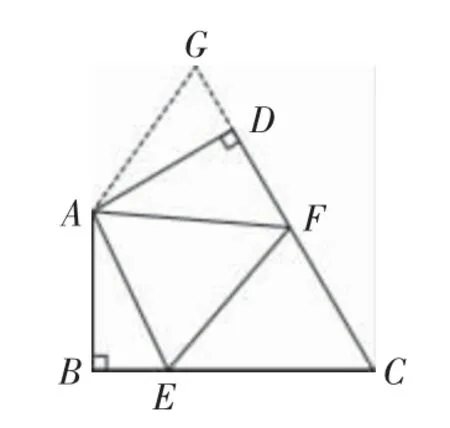
圖21

（1）自主發現：線段BE，EF，FD之間有何數量關系？請說明理由.

（2）探索延伸：如圖22，四邊形ABCD中，AB=AD，∠ABC+∠ADC=180°，E，F分別是BC，CD上的點，且∠FAE=∠DAB，（1）的結論是否仍然成立，請說明理由.

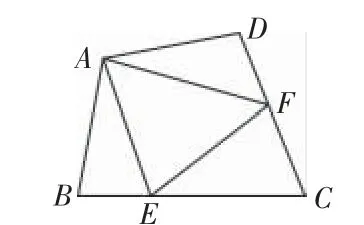
圖22

（3）實際應用：如圖23，在某次抗臺風演習中，船甲在A處，距離指揮中心（O處）北偏西30°，船乙在B處，距離指揮中心南偏東70°，且兩船到指揮中心（O處）的距離相等，接到指令后，船甲以60海里/小時的速度向正東方向前進，船乙以80海里/小時的速度沿北偏東50°的方向前進1.5小時后，指揮中心觀測到甲、乙兩船分別到達E，F處，此時兩船之間的夾角為70°，試求此時兩船之間的距離.（可結合（2）的結論）

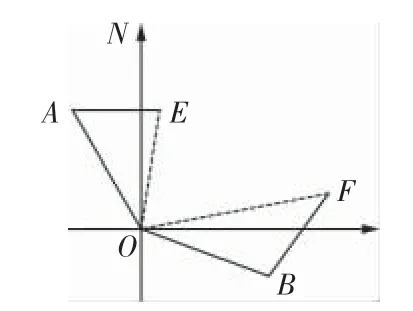
圖23

（4）你能像上題一樣將全等三角形應用于實際生活嗎？請舉例說明.

設計意圖引導學生體會全等三角形在證明線段或角相等、證明線段的位置關系、對圖形面積變換和實際應用問題上的作用，啟發學生碰到相關問題時能想到尋找對應的全等三角形，以及利用全等三角形解決生活中的實際問題，培養學生的應用意識與創新意識.

上述作業設計具有明顯的梯度原則，又依據解題方法進行分類，使每題都具有典型性.其中各模塊的側重點應有所不同：

“習題演練，自我提升”關注已有的活動經驗，突出基礎素養的落實；

“歸納總結，自我反思”關注解決問題的過程，突出數學思想的滲透；

“綜合應用，自我鞏固”關注關鍵能力的發展，突出應用意識的培養；

“拓展創新，自我突破”關注學生的主體作用，突出創新意識的提升.

同時，內容與中考考點緊密結合，讓學生感受知識點的實效性和針對性.

作業批改后的反饋

學生根據自身能力自主選擇完成提升型—反思型—應用型—拓展型作業，通過學生課后自主完成、課堂歸納總結、同伴交流提煉的形式進行反饋.其中提升型和反思型作業面向全體學生課后完成，應用型和拓展型作業則先獨立思考后以小組為單位交流合作完成.

由表2：四次作業的正確率基本由高到低，體現了難度的階梯設置.從正確率上看，提升型和反思型作業正確率較高，應用型和拓展型作業正確率相對較低，可見大部分學生具備一定的幾何直觀與推理能力，但部分學生應用意識和創新意識相對欠缺，在今后的教學中應重點關注這類學生.另外，要堅持“下要保底，上不封頂”的原則，對于本次反饋出的薄弱生以及尖子生，后續將繼續對應進行托底以及培優工作.

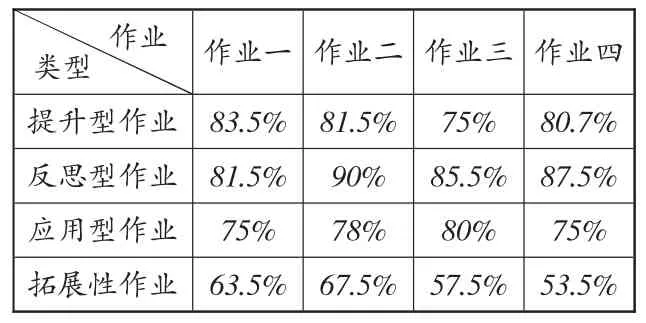
表2 作業各類型問題平均正確率

作業質量與成效分析

（一）作業質量

結合問卷調查，從以下幾方面對作業質量進行分析：從作業量上看，題量基本控制在6題以內；從完成時間上看，學生完成作業時間大部分為20分鐘；從作業難度上看，學生認為作業難度適中，大多數題可以從上一題的微小變化中找到思路；從學習興趣上看，學生認為能在完成作業的過程中體會到成功的快樂，在交流環節中能和同伴擦出更多思維的火花，極大促進了學習數學的興趣.

（二）成效分析

以初二甲、乙兩班作為實驗對象，在新課結束后的前測中兩班水平相似，而后實驗班安排階梯式單元提升作業，對照班仍使用傳統作業.實施期間，每天統計兩班作業情況，關注作業的布置、批改與反饋，保證有效實施.后測安排在提升作業完成并講解后，兩班學生以同等標準作答，統計兩班的平均分、優秀率，對比各層次人數的變化，分析階梯式單元提升作業實施對學習效果的影響.

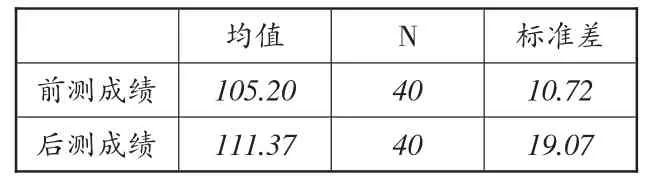
表3 成對樣本統計量

將實驗班前測與后測成績進行比對分析可知：實驗班在平均分有所提高，標準差升高，說明學生成績的波動幅度大，變化顯著，并成正態分布.

由表4可知：相關系數為0.615，p=0.000＜0.05，說明實驗班學生前測與后測成績具有相關性.

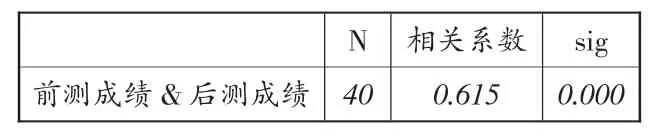
表4 成對樣本相關系數

觀察表5每個分數段對應的學生人數、平均分、優秀率，可見在單元新課結束時實驗班和對照班學生在掌握知識方面和綜合能力方面都相對良好，水平相當.

表5 前測成績統計結果

由表6可知：經過階梯式單元提升作業的訓練，實驗班得分在90以下的人數減少，得分105～120的人數得到大幅增長，平均分和優秀率都明顯高于對照班，說明實驗班相較對照班總體學習狀態提升明顯，核心素養與關鍵能力有明顯發展，基于學情的階梯式單元提升作業取得了良好的實驗效果.

表6 后測成績統計結果

總結與展望

在“雙減”的背景下，作業的優化設計必定會成為一線教師需要認真思考的長久課題.本文提出的基于學情的階梯式單元提升作業設計也僅僅只是筆者短期內的實踐所得，具體長遠的成效以及在數學其他領域的應用作用仍需時間進行考證與探究，我們將繼續完善“減負提質”的作業設計，依據學科學習目標要求，學生學情實際，不同學習期待水平，內容整合的程度、要求和形式的多樣性，探索設計促進核心素養發展、以學生學習為中心，基于單元大問題、大任務的問題情境，進一步關注目標與內容、關注進階與組合、關注結構與本質、關注遷移與創新，將減負增效真正落到實處.