譜V（1）同倫群中的一個新元素

蔡玉梅，王玉玉

（天津師范大學數學科學學院，天津 300387）

1 引言和主要結果

同倫群是拓撲空間的幾個基本的代數不變量之一.相較于同調群，同倫群的計算十分困難，也成為代數拓撲的重要問題之一.對于簡單的不可縮空間球面，對其同倫群，特別是穩定同倫群的研究具有重要意義，近幾年的相關成果參見文獻[1-4].

記A為模p的Steenrod代數，P為由所有A的循環縮減冪pi（i≥0）生成的子代數.對于連通有限型譜X、Y，存在Adams譜序列{Ers，t，dr}[5]，滿足：

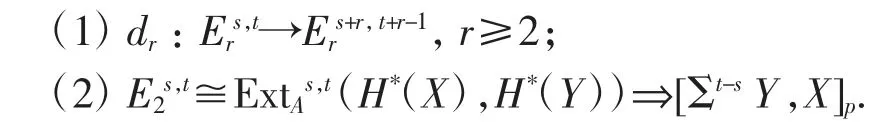
其中E2s，t是A的上同調.當X為球譜S、Moore譜M、Toda-Smith譜V（1）時，πt-s（X）p分別為S、M、V（1）穩定同倫群的p局部.在利用Adams譜序列求解同倫群的過程中，需計算有關ExtAs，t（H*（X），H*（Y））的結果，本文利用May譜序列并結合譜的上纖維序列導出Ext群的正合序列來解決.

Toda-Smith譜V（n）的Zp上同調群為

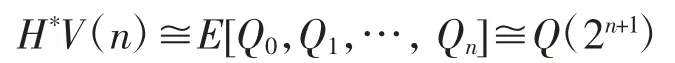
其中：Qi（i=0，1，…，n）為模p Steenrod代數A的Milnor基元；E[]為外代數；Q（2n+1）為2n+1維的Zp向量空間，且其Zp基為

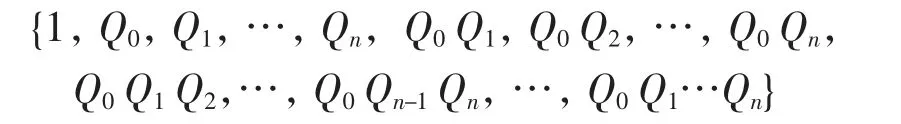
由文獻[6]可知，V（n）是可實現的，當n=0、1、2、3，且p＞2n時，存在上纖維序列：

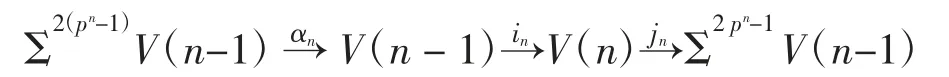
其中：V（-1）=S；α0、α1、α2、α3分別為p、α、β、γ.由于存在短正合序列：

所以上面的上纖維序列可以導出Zp上同調群的短正合序列：

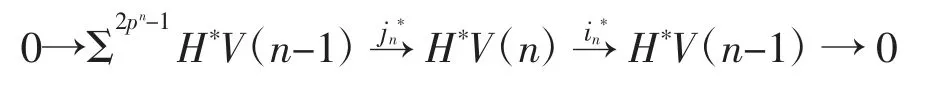
進一步可導出Ext群的長正合序列：

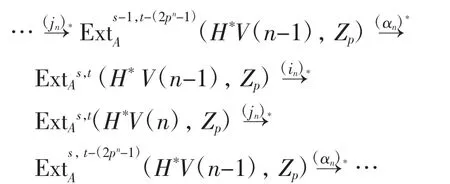
綜上可見，Toda-Smith譜與球譜S通過一些上纖維化存在密切聯系.因此，它們的同倫群中元素的存在性也相互關聯.本文發掘了譜V（1）同倫群中的一個非平凡元素，它在Adams譜序列中由h2表示，與文獻[7]不同，本文利用代數和數論的方法給出了h2的收斂性，該方法更具可操作性和應用的廣泛性.

ExtAs，t（Zp，Zp）（s=1、2、3）的Zp基的情況見文獻[8-9]，其中

本文的主要結果如下.

定理令素數p≥7，則元素

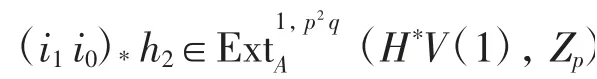
在Adams譜序列中是永久循環的，且收斂到π*V（1）中的非零元.

2 Ext群的一些結果

命題1[10]當t-s＜2p4-1時，ExtAs，t（H*V（3），Zp）?ExtPs，t（Zp，Zp）.

推論Zp），r≥2.

命 題2[6]Rank（ExtPs，t（Zp，Zp））≤Rank[P（bji）?H*，*（U（L））]s，t，其中：[P（bji）?H*，*（U（L））]s，t為May譜序列的E2-項，P（bji）為多項式代數.

命題3當p≥7，r≥2時，

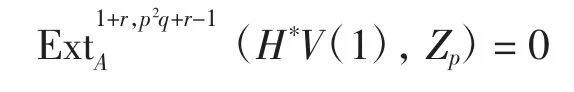
證明由推論可得

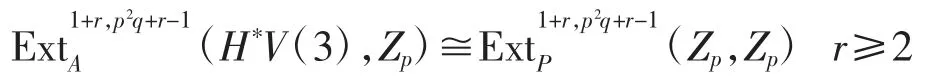
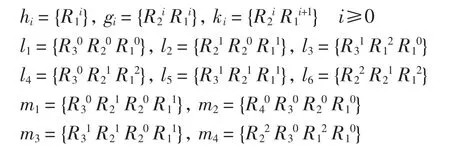
對于加法有

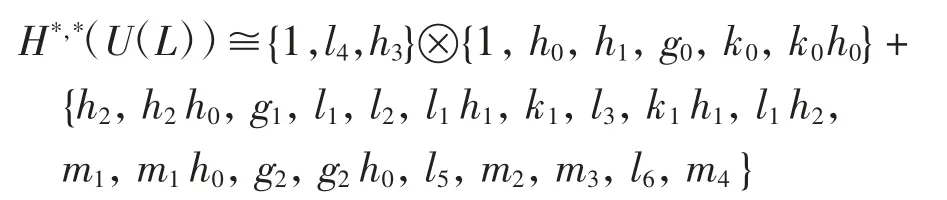
且Rji和bji的雙次數分別為（1，2（pi+j-pi））和（2，2（pi+j+1-pi+1））.在May譜序列中，b10收斂到b0∈ExtP2，pq（Zp，Zp），b10的全次數為|b10|=pq-2.將[P（bji）?H*，*（U（L））]s，t中全次數不大于p2q-2的生成元λ，及其全次數|λ|（mod pq-2）的余數列出，見表1.

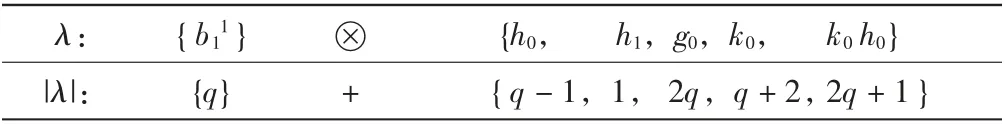
表1 生成元λ及其全次數|λ|（mod pq-2）的余數Tab.1 Generator λ and the remainder of total degree|λ|（mod pq-2）

由于|（i3）*（i2）*（x）|=p2q-2≡q（mod pq-2），由表1可知，在May譜序列的E2-項[P（bji）?H*，*（U（L））]s，t中存在滿足條件的元λ可能為b11，其全次數為p2q-2，雙次數為（2，p2q），即當r=1時，（i3）*（i2）*（x）=b11，與r≥2不符，故排除.此時有0，所以（i3）*（i2）*（x）=0，再由長正合序列：

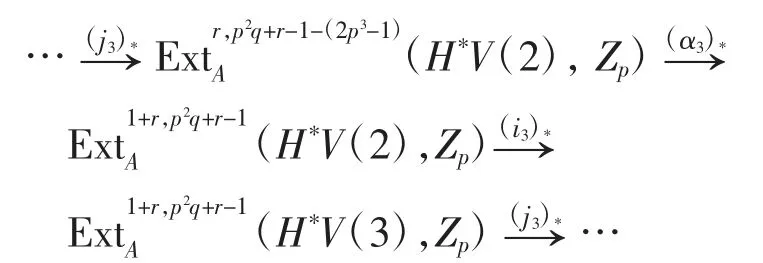
可知（i2）*（x）=（α3）*（x1），其中

所以

對于zk，有

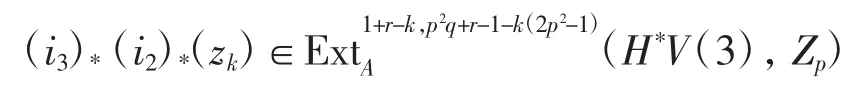
其全次數為

（1）當k=1時，Q=-2（mod pq-2），由May譜序列的E2-項的各個生成元及其次數列表可知滿足此條件的元不存在，故（i3）*（i2）*（zk）=0.

（2）當1＜k＜p-2時，

Q=（1+p-k）q-（2k+2）（mod pq-2）或者

Q=（p-k）q+（q-2k-2）（mod pq-2）滿足前者顯然無對應元.對于后者，可能存在對應元k0h0b11，但其全次數為p2q+2pq+2q-5，大于（i3）*（i2）*（zk）的全次數，所以這種情形無對應元，故（i3）*（i2）*（zk）=0.

（3）當k=p-2+r時，其中：r=0、1，Q=（2-r）q-2r（mod pq-2）.

①當r=0時，Q=2q（mod pq-2），由表1知λ可以為g0，其全次數為pq+2q-2，與（i3）*（i2）*（zk）的全次數不相等，故（i3）*（i2）*（zk）=0.

②當r=1時，Q=q-2（mod pq-2），此時沒有滿足與其次數對應的元，因此（i3）*（i2）*（zk）=0.

（4）當k＞p-1時，|（i3）*（i2）*（zk）|＜0，易知（i3）*（i2）*（zk）=0.

綜上可得

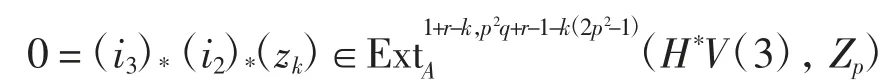
由正合性，存在

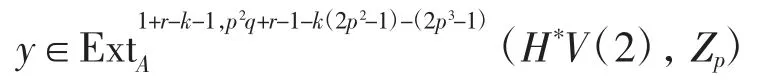
滿足（α3）*（y）=（i2）*（zk），但此時

所以y=0，故（i2）*（zk）=（α3）*（y）=0.因此，存在

滿足（α2）*（zk+1）=zk，即

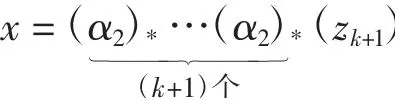
歸納完成.

取k=p+1，則

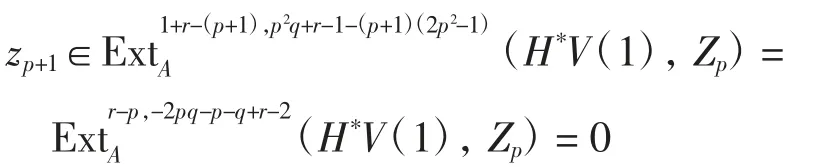
命題4當p≥7，r≥2時

證明當r≥2時，命題顯然成立.

3 定理的證明

考慮Adams譜序列，其E2-項

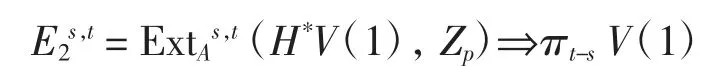
微分為dr：Ers，t→Ers+r，t+r-1.由命題3有

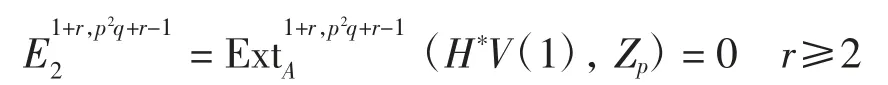
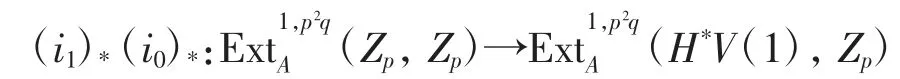
在映射下的像為（i1i0）*h2，則r≥2.因此

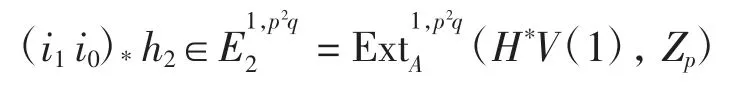
在Adams譜序列中是永久循環的.由命題4有