小型降落傘充氣和傘衣塌陷過程

張延泰，孫建紅，2，侯 斌

（1.南京航空航天大學 飛行器環境控制與生命保障工業和信息化部重點實驗室，南京 210016；2.南京航空航天大學民航學院，南京 210016）

馬航370航班失聯后，南京航空航天大學民機救生團隊與中國商用飛機有限責任公司（中國商飛）針對民航客機聯合研發了分離式應急記錄跟蹤系統，該系統又被稱為報信者（harbinger，HBG）系統[1-4].在HBG系統中，應急飛行數據記錄器（emergency flight data recorder，EFDR）在飛機墜毀前彈射離機.利用降落傘可以有效降低EFDR墜落速度，減小墜落沖擊.降落傘離機后迅速開傘，其傘衣充氣過程較為復雜[5]，而針對小型裝置設計的降落傘不多，對其展開過程的研究相對較少，其中小型傘是否存在傘頂塌陷及其塌陷機理均缺乏細致研究.如果小型傘傘衣在充氣階段發生塌陷或扭曲變形，盡管是局部也可能會導致開傘失敗.研究小型降落傘充氣過程，分析傘衣附近的流場特性，判斷其工作充氣過程中的安全性對小型裝置投放等工程應用具有重要意義.

降落傘在充氣過程中，流體與傘衣的耦合作用具有非定常、柔性大變形等非線性特性，是流固耦合研究的難點之一.降落傘充氣過程的理論模型最早出現于1927年，是后續降落傘充氣過程計算方法的基礎.在此基礎上，Mohaghegh等[6]研究了降落傘的充氣過程，發現充氣時間與傘型、傘口面積和來流速度等因素相關.這些充氣模型多用于計算充氣時間和開傘動載，沒有考慮傘衣局部變形等問題.Wolf等[7]研究了群傘的充氣過程，發現減速傘充滿后發生塌陷會嚴重影響傘衣的減速效果.隨后，NASA在獵戶座計劃中[8]發現傘衣在充氣過程中存在過度充氣和部分塌陷的問題.在實驗的基礎上，Yavuz[9]針對物傘系統和傘衣尾流區速度分布建立了理論模型.彭勇等[10]基于流體連續方程和動量方程，提出了降落傘充氣過程的尾流再附動力學模型.在試驗與仿真結合的研究中，王海濤[11]研究了大型降落傘充氣過程中的傘衣變形和抽打現象，分析了抽打現象的特點和形成原因.

此外，利用實驗和數值模擬技術可以進一步分析傘衣附近流場特性對傘衣變形的影響.Johari等[12]采用PIV和水洞試驗技術研究了降落傘的尾流場，認為渦脫落對傘衣背部有周期性的吸力作用.Fang等[13]采用數值模擬方法研究了十字傘的充氣過程，對比分析了單傘和雙傘系統，討論了傘衣附近流場特性對傘衣充氣過程的影響.孫建紅等[14]針對阻力傘實驗中的非定常運動和尾流干擾，結合理論分析和數值模擬技術，分析了附加質量模型，建立了傘衣阻力系數的修正方法，并與實驗結果進行了對比分析.

綜上所述，研究人員在較早的工程應用中發現并討論了尾流再附與傘衣塌陷等問題，但研究主要關注傘衣投影直徑、充氣時間和開傘載荷的變化.針對小型降落傘的流場特性與傘衣變形相互作用的研究相對較少.本研究對小型降落傘的充氣和傘衣塌陷過程進行數值模擬，分析了傘衣充氣過程中流場特性和傘衣變形的演化規律，研究了來流速度和前置體質量對傘衣充氣過程的影響，以期給出傘衣安全充氣的工況范圍.

1 數值計算方法

降落傘的充氣過程是柔性體大變形流固耦合問題，可采用ALE方法進行數值模擬，通過罰函數方法進行流固耦合計算.根據美國國家運輸安全委員會（national transportation safety board，NTSB）的事故報告，本研究工況中，設置HBG系統降落傘的開傘速度區間為40～160 m/s，可壓縮流體控制方程為

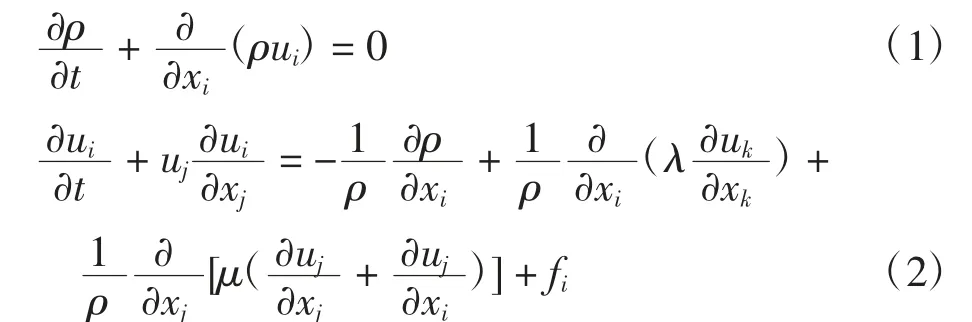
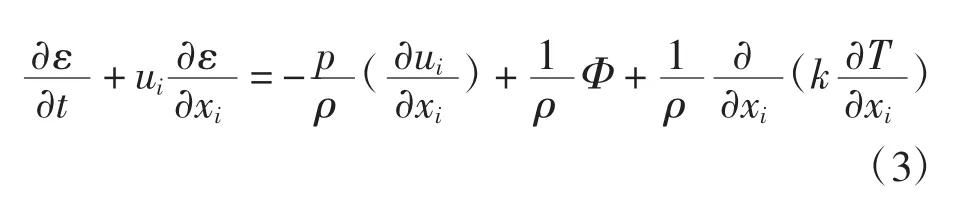
式（1）～式（3）中：t為時間；ρ為流體密度；ui為流體速度張量；p為流體壓力；fi為體積力張量；ε為流體比內能；Φ為耗散函數；T為流體溫度.

由于ALE方法在歐拉和拉格朗日坐標之外引入了參考坐標，所以在ALE方法中，材料域的節點信息需要被映射到空間域內，其流場變量的輸運方程為

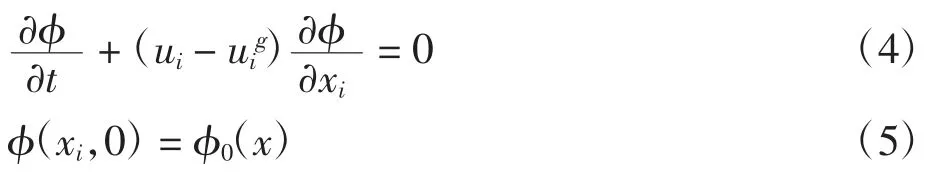
式（4）和式（5）中：φ為流場變量；φ0為當前時間步流場變量的初始值；uig為材料速度張量，當uig=0時對應歐拉方法，當uig=ui時對應拉格朗日方法.該數值模擬方法在本課題組前期研究中用于分析降落傘和阻力傘的充氣過程[5，15].因此，有理由認為該數值模擬方法適用于本研究.

2 計算模型

HBG系統的降落傘為平面圓形傘，傘衣名義直徑為1.9 m.根據平面圓形傘的折疊方法，傘衣首先按照傘衣幅做“平折疊”，隨后做“Z字形”折疊，最后放入傘包.在數值模擬中采用類似真實平面圓形傘折疊的方法進行建模，圖1為傘衣折疊前后的面積變化和折疊后的傘衣網格.由于降落傘掛載的電子設備體積較小，所以計算模型中將前置體簡化為1個質點.計算域尺寸為6D0×6D0×15D0，在傘衣充氣區域進行局部加密，總網格數約為2.6×106個，為保證質量守恒，計算域邊界采用速度入口.

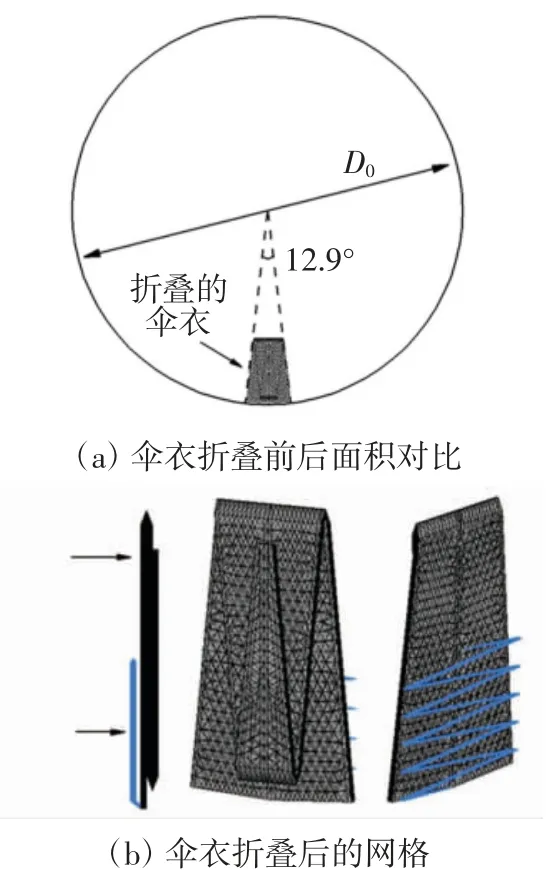
圖1 數值模擬中的降落傘折疊模型Fig.1 Parachute folding model in numerical simulation

3 結果與分析

3.1 流場分析

由于大型降落傘充氣過程中的劇烈變形可能導致傘衣破損或開傘失敗[16]，而HBG系統的電子設備質量較小，因此可采用小型降落傘完成緩降功能.小型降落傘的剛度較大，其開傘過程與大型降落傘存在明顯區別.為了闡明HBG系統小型降落傘的充氣過程，首先以來流速度為100 m/s、電子設備質量為4 kg的工況為代表，研究傘衣充氣過程的流場特性.

研究表明，傘衣外形變化與剪切層和近尾跡區渦結構等的演化密切相關[14].圖2為來流速度為100 m/s時，傘衣充氣過程的外形變化與壓力云圖，采用速度等值線的方法描繪出剪切層的位置和形態.

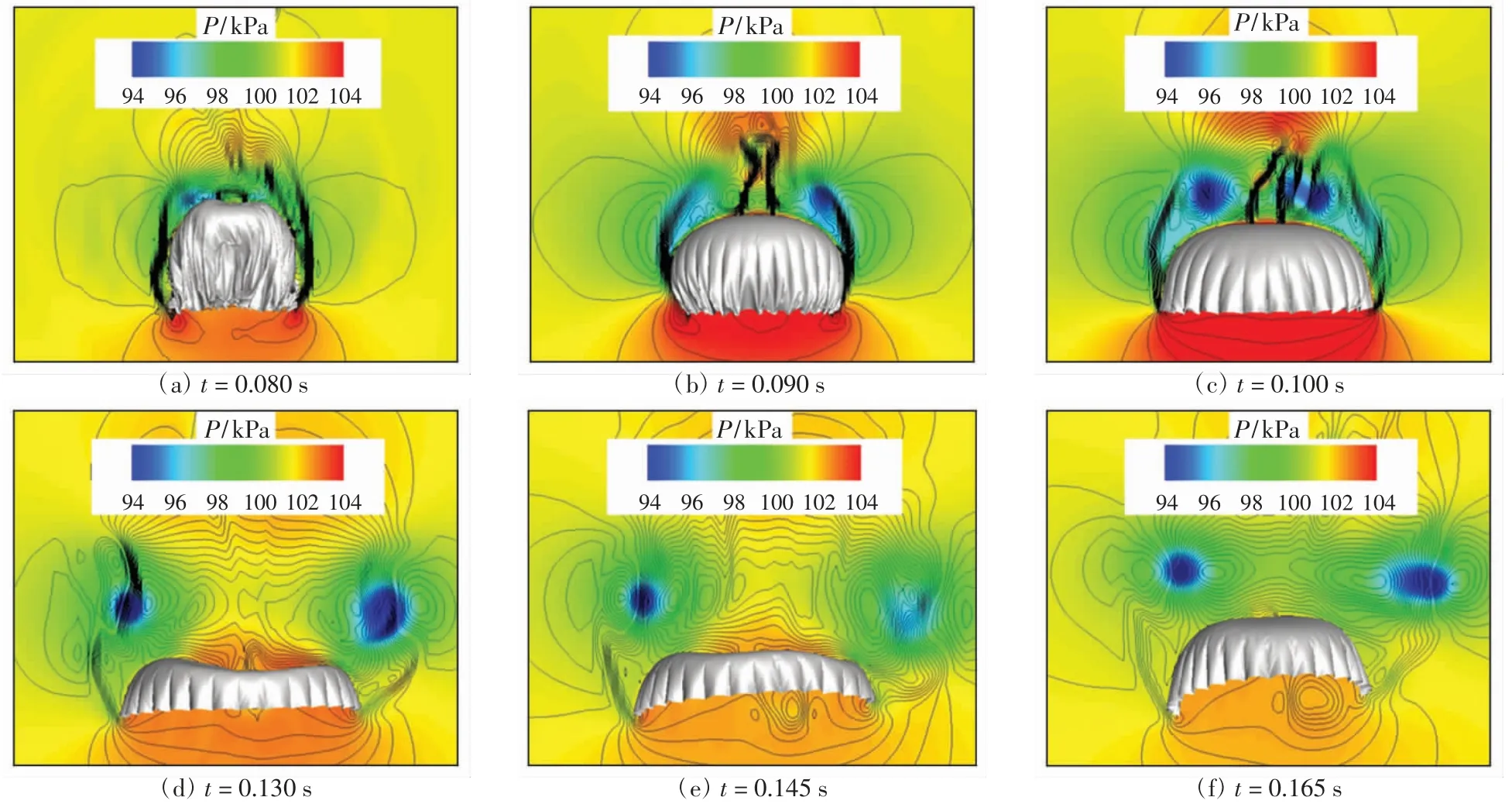
圖2 傘衣對稱面的壓力云圖Fig.2 Pressure contour of symmetrical plane of parachute

由圖2（a）可以看出，當傘衣呈“燈泡”狀時，剪切層在傘衣底邊形成并緊貼于傘衣側面.當剪切層發展到傘衣肩部時，傘衣發生分離并迅速失穩（圖2（a））.隨著傘衣擴張，剪切層的分離點逐漸向傘衣底邊移動（圖2（a）～圖2（d））.同時，剪切層失穩后卷起的尾渦也在向傘衣外側移動.在尾渦由中心向外側移動時，傘衣頂部出現了高壓區（圖2（d）），說明傘衣在充氣過程中出現了尾流再附現象.尾流再附造成傘衣在傘頂孔附近出現非對稱的局部塌陷，加劇了傘衣近尾跡區流場的非對稱特性，導致傘衣沿徑向發生偏轉（圖2（f））.

為了進一步研究傘衣充氣過程中流場演化的動力學特征，采用Lamb矢量散度描述傘衣附近流場特性[15].Lamb矢量散度定義為Δ·L，其中L=ω×u為Lamb矢量，ω為偽渦矢量，u為流體速度矢量.圖3為流向速度為100 m/s時利用Δ·L描述的流場拓撲結構.由圖3（a）～圖3（c）可知，在傘衣側面的剪切層中，Δ·L出現了明顯的正負雙層結構.該結構的動力學過程包含了強應變率區和渦量區間的相互作用[15].尾流再附發生后，傘衣側面的Δ·L雙層結構演化為正負交替結構（圖3（d）～圖3（f））.該正負交替結構一般出現在鈍頭體繞流的近尾跡區中，說明此時剪切層在傘衣底邊形成后不能穩定地向下游發展，而是會迅速失穩.這種流場演化現象與無限質量充氣過程明顯不同.在無限質量充氣過程中，當傘衣投影面積達到峰值后，剪切層和尾渦會進入周期性演化[17].而在HBG系統小型降落傘的有限質量充氣過程中，傘衣側面剪切層不會進入周期性演化，而是出現劇烈的渦運動和流體拉伸變形運動.

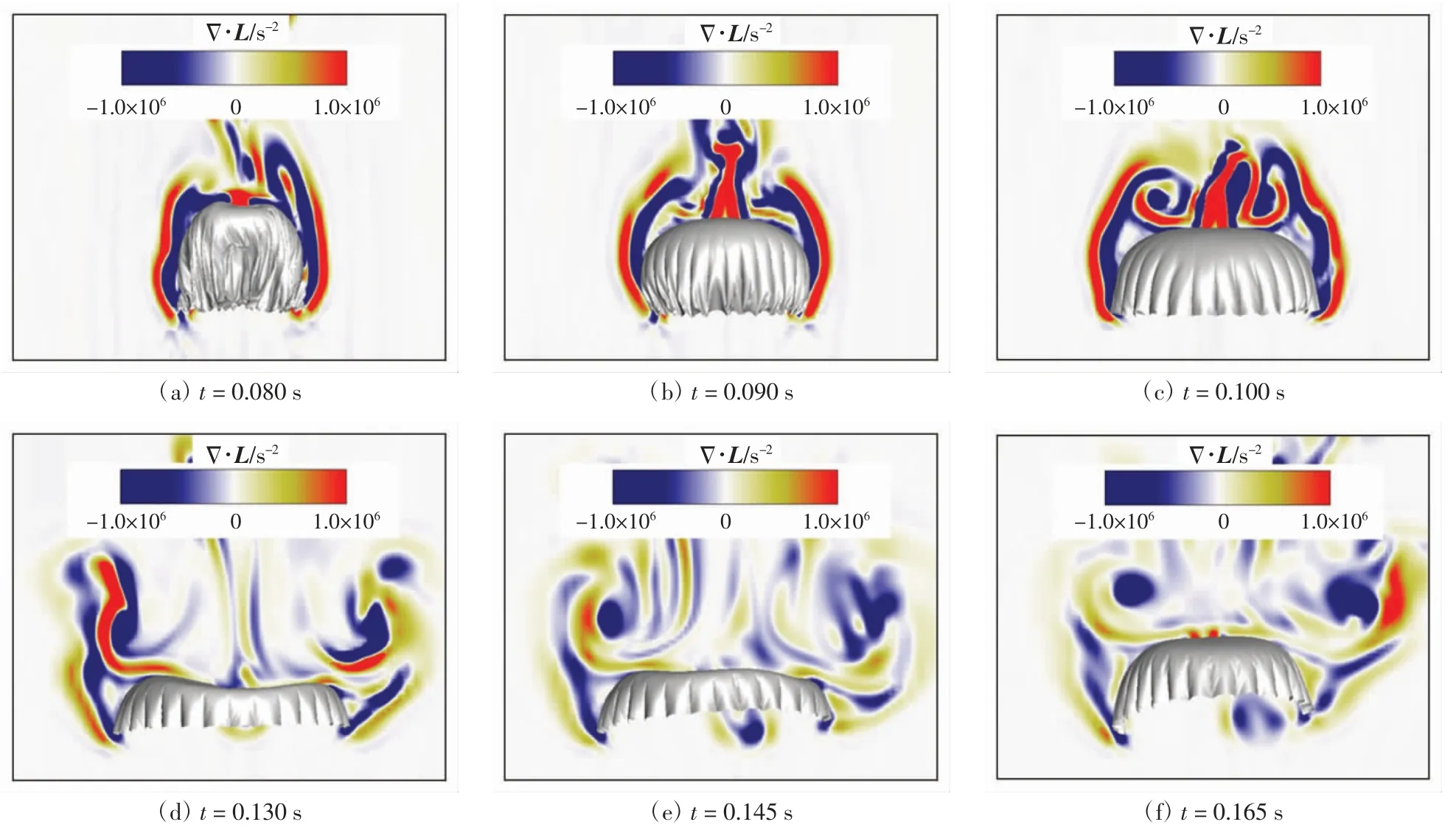
圖3 傘衣對稱面Lamb矢量的散度云圖Fig.3 Lamb vector divergence contour of symmetrical plane of parachute

HBG系統的降落傘具有前置體質量小、傘衣面積小的特點，其開傘過程屬于有限質量充氣.Desabrais[17]從流場特性演化的角度將降落傘充氣過程劃分為3個階段.與Desabrais[17]研究的無限質量充氣過程相比，HBG系統降落傘充氣過程前2個階段的流場特性和傘衣外形變化特征是非常相似的.而在無限質量充氣的第3個階段，傘衣側面的剪切層開始周期性演化，傘衣產生周期性的“呼吸”現象.與此不同，HBG系統降落傘在第3階段出現了尾流再附，導致降落傘在充氣過程的后2個階段中，剪切層不會進入周期性演化，流場的非對稱特性也比無限質量充氣更明顯.

圖4為流向速度為100 m/s時，HBG系統降落傘充氣過程中動載和傘衣投影面積的變化曲線.

圖4 傘衣充氣過程中的動載與投影面積Fig.4 Load and projected area of parachute during inflation

由圖4可以看出，根據流場演化的特點，充氣過程可以被分為4個階段.第1個階段為0～0.060 s，傘繩和傘衣從折疊狀態拉直，傘繩的拉直力使動載出現第1個峰值；第2個階段為0.060～0.080 s，傘衣底邊首先開始充氣擴張，隨著氣流進入傘衣并在傘頂聚集形成高壓區，傘衣頂部開始擴張出現“燈泡”狀；第3個階段為0.080～0.130 s，此階段內傘衣投影面積迅速增大，開傘動載出現峰值，隨后由于尾流再附，傘衣頂部出現局部塌陷；第4個階段為0.130～0.165 s，傘衣從傘頂局部塌陷的狀態逐漸回彈，在非對稱流場的影響下，傘衣在沿軸向運動的同時沿徑向發生偏轉.在大型降落傘的空投實驗中，傘頂在塌陷后的回彈過程中，可能發生傘衣纏繞造成嚴重破損[11].由于HBG系統降落傘尺寸較小，雖然傘頂在充氣過程中發生了塌陷和回彈，但并沒有纏繞其他部分傘衣.

3.2 前置體質量和來流速度對降落傘充氣過程的影響

由前文分析可知，在典型工況下，HBG系統的小型降落傘在回彈過程中不會發生傘衣纏繞.為了進一步分析該小型降落傘在充氣過程中的安全性，需要給出前置體質量和來流速度等因素對傘衣充氣過程的影響.根據環縫傘相關研究[18]可知，尾流再附現象與物傘系統的質量比和速度比相關，質量比和速度比分別為

式（6）和式（7）中：m為前置體質量；ρ為流體密度；D0為傘衣名義直徑；U∞為來流速度；UF為緩降速度.

現役飛行數據記錄器質量約為6～12 kg，在HBG系統中，離機緩降的電子設備質量小于傳統飛行數據記錄器.電子設備在飛機墜毀前彈射離機，假設來流密度為1.225 kg/m3不變，當來流速度為100 m/s（UR=0.5）、傘衣名義直徑為1.9 m時，改變電子設備質量，分別取質量比為0.2、0.5、0.8、1.1和1.4的工況進行分析.圖5為流向速度U∞=100 m/s、不同質量比RN時，傘衣在充氣過程第3和第4階段內的外形變化.

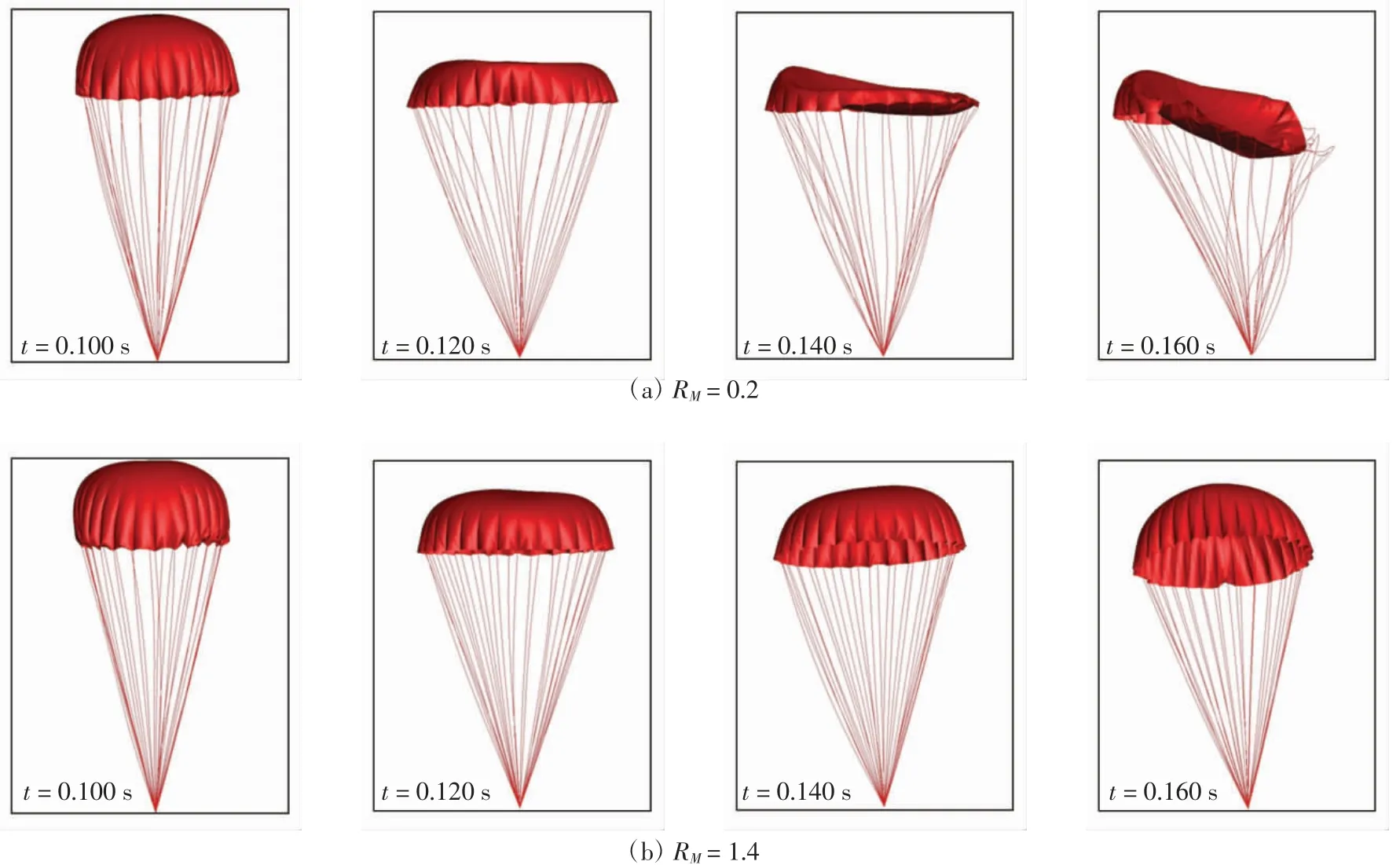
圖5 不同質量比時，傘衣充氣過程中的外形變化Fig.5 Shape change of parachute during inflation with different mass ratio

由圖5可以看出，在0～0.120 s的時間內，不同質量比工況下，傘衣外形的變化規律相近.在傘衣充氣過程的第3階段，均出現了傘頂的局部塌陷.當RM=0.2時，頂部局部塌陷后，傘衣塌陷的范圍逐漸變大，最終導致全部傘衣劇烈變形.當RM=1.4時，頂部局部塌陷后，傘衣回彈，沒有出現傘衣完全塌陷的現象.

流向速度U∞=100 m/s時，開傘過程中的傘衣投影面積如圖6所示.

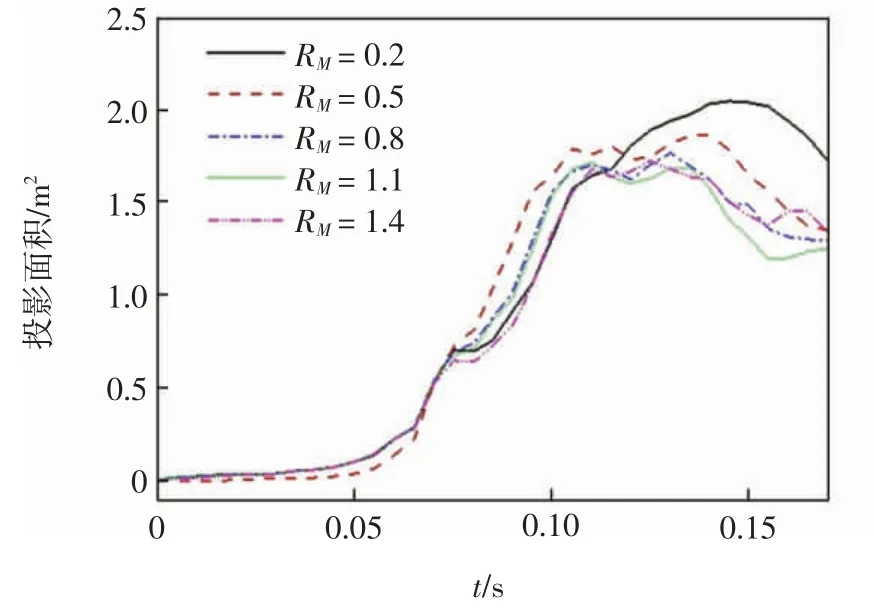
圖6 質量比對傘衣投影面積的影響Fig.6 Effect of mass ratio on projected area of parachute

開傘過程的前0.070 s是傘衣傘繩的拉直過程，由于傘衣底面充氣口面積較小，傘衣充氣速度較慢，導致傘衣投影面積變化較小.隨后傘衣充氣過程進入第2個階段，大量空氣沖入傘衣，造成傘衣投影面積迅速增加.在充氣過程的最后階段，當RM=0.2時，傘衣大面積塌陷使其投影面積明顯大于其他工況.由圖6可以看出，當RM=0.2時，傘衣投影面積峰值明顯大于其他工況.當RM=0.5～1.4時，傘衣投影面積的變化曲線相近，說明在0.5＜RM＜1.4工況中，不會由于尾流再附導致傘衣大面積塌陷，是較為安全的工況.

為了進一步說明前置體質量不同時，傘衣充氣過程的流場特性，圖7給出了流向速度U∞=100 m/s時，傘衣充氣過程第3和第4階段典型時刻的壓力云圖.由圖7可以看出，t=0.100 s時傘衣附近流場特性相近，剪切層在傘衣底邊形成后向下游發展.在傘衣的近尾跡區中，剪切層失穩并卷起旋渦.隨著傘衣充氣過程向第4階段發展，傘衣附近流場區別越來越明顯.在RM=0.2的工況中，由于前置體質量較小，在降落傘氣動力作用下，前置體向傘衣方向回彈，導致t=0.140 s時部分傘繩處于松弛狀態（圖7（a））.由于傘繩對傘衣的拉扯作用減小，傘衣難以保持類似半球殼狀的外形.對比RM=1.4、t=0.140 s時傘衣對稱面的壓力云圖（圖7（b））可以發現，RM=0.2時傘前氣體的高壓區域幾乎消失，說明此時傘衣對于來流氣體的滯止效應非常微弱.

圖7 不同質量比傘衣對稱面的壓力云圖Fig.7 Pressure contour of symmetrical plane of parachute with different mass ratio

本研究中來流速度為40～160 m/s，緩降速度為8 m/s，當前置體質量為4 kg（RM=0.5）時，分別取速度比RV為5.00、8.75、12.50、16.25和20.00的工況進行分析.圖8中給出了速度比RV為5.00和20.00的工況下，傘衣在充氣過程第3和第4階段的外形變化情況.圖9進一步給出了速度比RV為5.00、8.75、12.50、16.25和20.00的工況下，開傘過程中的動載和傘衣投影面積變化曲線.

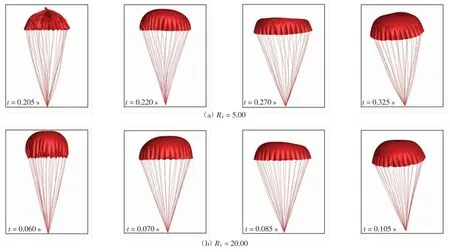
圖8 不同速度比時，傘衣充氣過程中的外形變化Fig.8 Shape change of parachute during inflation in different speed ratio

由圖8可以看出，在不同速度比的工況下，傘衣在充氣過程中均經歷了由充滿到傘頂塌陷再到傘頂回彈的外形變化過程.在傘衣充氣時，沒有出現傘衣完全塌陷的現象.為了方便對比分析，將動載峰值時刻定義為傘衣充滿時間，采用無量綱時間t/tf繪制傘衣投影面積變化曲線（圖9（b））.由圖9（a）可以看到，傘衣充氣時間隨著來流速度的增加而降低，同時動載峰值隨著來流速度的增加而上升.由圖9（b）可知，速度比不同時，傘衣投影面積的變化較為相似，說明在RM=0.5、5.00＜RV＜20.00工況下，傘衣在充氣過程中均未出現大范圍的傘衣塌陷現象，是較為安全的工況.

圖9 速度比對開傘動載和傘衣投影面積的影響Fig.9 Effect of speed ratio on opening load and projected area of parachute

4 結論

本文采用任意拉格朗日-歐拉（ALE）方法數值模擬了HBG系統降落傘的充氣過程，分析了傘衣充氣過程的流場特性，研究了前置體質量和來流速度對傘衣塌陷的影響，研究結果表明：

（1）根據流場演化的特點，傘衣的充氣過程可分為4個階段.其中，前2個階段的流場特性和傘衣外形變化特征與無限質量充氣過程非常相似.在充氣過程的后2個階段，剪切層不會進入周期性演化，流場的非對稱特性也比無限質量充氣更明顯.

（2）傘衣在充氣過程中出現尾流再附，并導致傘頂局部塌陷.若前置體質量過小，傘衣塌陷的范圍會逐漸變大，并最終導致全部傘衣劇烈變形，是較為危險的工況.當0.5＜RM＜1.4時，傘衣頂部局部塌陷后傘衣回彈，不會由于尾流再附導致傘衣大面積塌陷，開傘失敗的風險較小，是較為安全的工況.

（3）在較大的工況范圍內，當來流速度不同時，傘衣投影面積的變化規律較為相似.當5.00＜RV＜20.00時，傘衣在充氣過程中均未出現大范圍的傘衣塌陷現象，開傘失敗的風險較小，是較為安全的工況.