二維湍流熱對流最大速度Re 數特性及流態突變特征Re 數*

何建超 方明衛 包蕓?

1) (北京航空航天大學,航空科學與工程學院,北京 100191)

2) (中山大學,航空航天學院,深圳 518107)

本文計算系列二維湍流熱對流,Prandtl(Pr)數和Rayleigh(Ra)數范圍分別為0.25—100 和1×107—1×1012,研究Reynolds(Re)數的變化規律.以最大速度計算的Re 數與Ra 數存在標度律關系,但中間出現間斷.研究表明,大尺度環流形態由橢圓形到圓形的突變引起流動失穩,導致最大速度值間斷下降,影響Re 數變化趨勢的連續性.所有Pr 數對應的流態突變特征Re 數為常值,Rec 約為1.4×104,即當Re 數達到特征Rec 時,大尺度環流形態會發生從橢圓形到圓形的突變.間斷點對應的Rac 與Pr 數之間存在標度關系Rac-Pr1.5.對Ra 數進行補償平移,所有Pr 數的Re 與RaPr—1.5的變化曲線重合,不同Pr 數有相同的間斷臨界點位置,RacPr—1.5=109.

1 引言

熱對流現象廣泛存在于自然界和工業設計中,研究熱對流特性有重要的意義.Rayleigh-Bénard(RB)熱對流是從眾多熱對流過程中抽象出來的典型物理模型之一,是在一個封閉的空間內下底板加熱上底板冷卻產生熱對流運動和熱輸運的系統[1].RB 熱對流系統存在豐富而復雜的流動和熱輸運現象,一直受到國內外學者的關注和研究.

在RB 熱對流系統中,Rayleigh 數(Ra)、Prandtl 數(Pr)和寬高比(Γ)是控制系統的3 個重要無量綱參數,而Nusselt 數(Nu)和Reynold 數(Re)分別是反映系統傳熱效率以及湍流強度的無量綱參數.多年來,兩個響應參數與控制參數之間的關系是RB 熱對流的研究重點[1-3],而其中影響最廣泛的是Grossmann 和Lohse 提出的GL 理論[4-8].GL 理論在較大范圍內預測了Nu(Ra,Pr)和Re(Ra,Pr)的變化趨勢,至今也得到了比較多數據的驗證[8-10].在GL 理論中,Ra-Pr相圖被分為多個區域[4,8],在不同區域中耗散率與Ra,Pr的關系有所差異.也即,在同一Pr數下,隨著Ra數增大,耗散率的發展趨勢會出現變化,其他相關的物理量的行為也會有所變化[11].早期關于RB 熱對流的研究中,發現到達臨界Ra數Rac(1707)之后,流體運動會從一種定常(time-independent)狀態轉換變為隨時間變化的非定常狀態[11-15],而這個轉變的Ra數與Pr數存在依賴關系[12].“芝加哥對流實驗”[16-18]發現隨著Ra數的增大,系統的流態會從對流狀態變為湍流狀態,同時系統的Nu數和Ra數關系也發生了轉變.其中,當RB 系統轉變為湍流狀態后,系統中的主要結構,包括羽流、大尺度環流等,會隨著Ra增大而發生突變[19-20].當大尺度環流由橢圓形轉變為圓形時,系統的Nu數也會偏離GL 理論預測曲線[10],但在更大的Ra后,Nu數的變化趨勢再次與GL 理論預測的一致[19-20].

有數值模擬研究[21]表明不同Pr數下,Re與Pr的標度律會出現變化,而Re與Ra的標度律均為0.53,與之前[18,22]獲得的0.46 不同.最近,在準二維的實驗中Li 等[23]在Pr=11.7—145.7的范圍內發現Re的標度律在0.53—0.60 之間,與Chen等[24]在Pr=4—7 之間發現的0.55 十分接近.在二維DNS 中,Xu 等[25]發現在Pr=0.025 時Re與Ra的標度律為0.50,而Werne 等[26]在Pr=7 時的標度律為0.54.這些研究表明,Re(Ra)的關系也會隨Pr數變化而略有變化,這變化值得去進一步深入研究.

本文采用高效并行直接求解方法PDM-DNS[27],在“天河二號”超級計算機上進行了多組Pr數和Ra數的二維湍流熱對流DNS 模擬,Pr數從0.25到100,Ra數范圍為1×107—1×1012,跨度為5 個量級,總共133 個計算算例.本文對多組Pr數和Ra數的二維湍流熱對流中反映湍流特性的Re數變化規律進行研究,并探討熱對流流態突變時對應的典型特征Ra數和Re數的特性及其變化規律.

2 二維湍流熱對流DNS的并行直接求解

在RB 熱對流的數值模擬中,通常引入Oberbeck-Boussinesq(OB)近似,對方程進行簡化.在OB 近似下,無量綱化的熱對流方程為

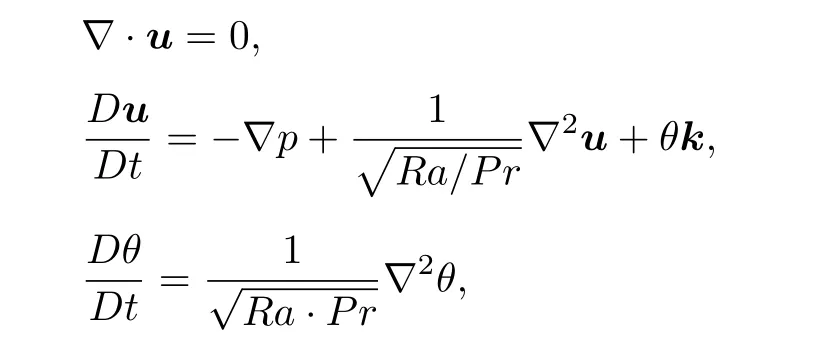
其中,u為無量綱速度矢量,θ為無量綱溫度,p為壓力,k為單位垂向矢量,方向與重力方向相反.數值計算中邊界條件為壁面速度均采用無滑移條件,溫度為側壁采用絕熱條件,上下底板采用恒溫條件,上底板恒溫冷卻θtop=?0.5,下底板恒溫加熱θbot=0.5.

大規模湍流熱對流的DNS 計算由于計算量巨大必須通過并行計算進行,其中壓力泊松方程的并行求解是實現高效并行計算的關鍵.利用高效并行直接求解壓力泊松方程的PDD 算法[28],建立了熱對流DNS的并行直接求解方法(parallel direct method of DNS,PDM-DNS),并展現了很好的并行效率[27].在數值求解過程中,采用投影法進行計算,時間和空間均是二階精度;壓力泊松方程采用快速傅立葉變換(FFT)進行解耦,然后直接求解三對角方程組,而動量方程和溫度方程采用顯式格式推進.

本文使用高效的PDM-DNS 方法,在“天河二號”超級計算機上進行了多組Pr數和Ra數的2D 湍流熱對流DNS 模擬.圖1 給出了計算算例的Ra-Pr相圖.本文中研究的Pr數從0.25 到100,Ra數從1×107到1×1012,跨度為5 個量級,總共133 個計算算例.本文的二維湍流熱對流計算數據豐富,相圖中呈現的結果是目前二維RB 系統較完整的數據.

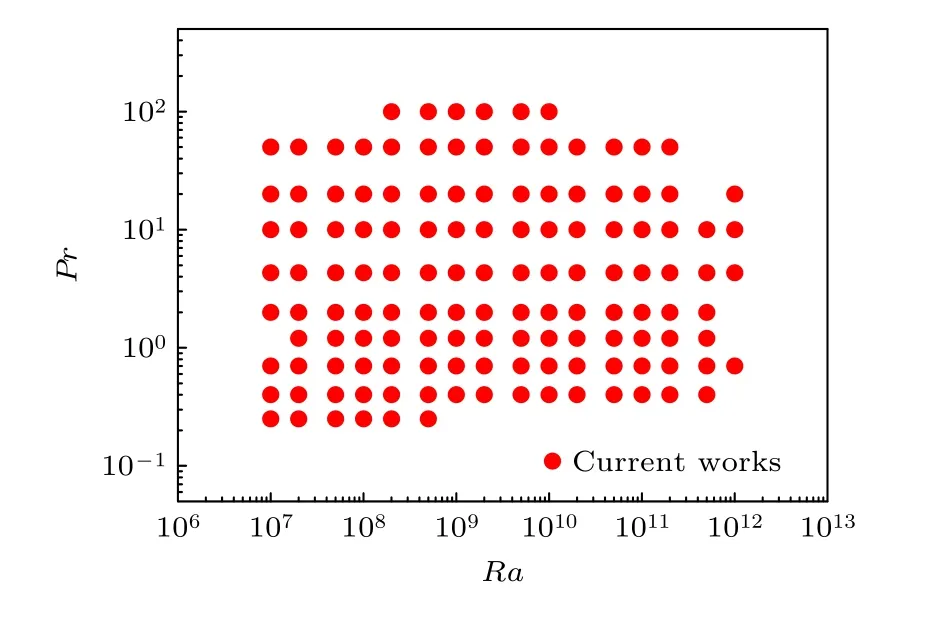
圖1 二維熱對流計算算例Ra-Pr 相圖Fig.1.The Ra-Pr Phase diagram explored in the present study.

為了充分識別系統的流動,本文采用了上下邊界加密的網格進行數值模擬,計算網格大小滿足Kolmogorov 尺度和Batchelor 尺度,即ηK=并且,邊界附近的網格滿足Shishkina 等[29]提出的要求,即:

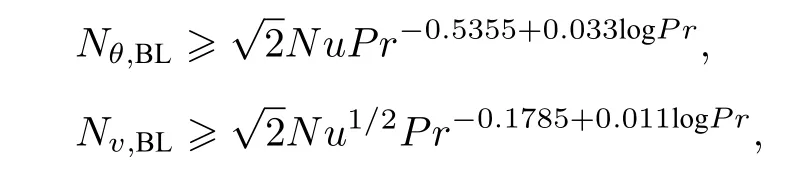
其中,a≈ 0.482,Nθ,BL和Nv,BL分別表示溫度邊界層和速度邊界層內的最少網格數.時間步長Δt小于Kolmogorov 時間尺度τK的1/1000.本文所有算例均在流場充分發展后進行統計,統計時間均大于200 個無量綱時間,并且在不同統計時間段求出的Nu數誤差約為1%[20].

在本文的算例中,有少數算例會出現大尺度環流翻轉的情況,具體包括Pr=1.2,Ra=2×107,Pr=2.0,Ra=1×107—1×108,Pr=4.3,Ra=5×107—2×108,Pr=100,Ra=2×108,共9 個算例.當僅統計順時針旋轉或逆時針旋轉的Re數和Nu數時,兩者的結果是一致的.因此,可以將順時針旋轉的數據進行水平翻轉,疊加到逆時針的旋轉的數據上,得到時間更長的時間平均場.如果統計數據包括大尺度環流的翻轉過程,并且不作方向統一的處理,那么將對數據統計造成一定的影響,比如Re數會減小約50%,Nu數波動約為3%[30].因此,關于翻轉算例的統計,僅統計順時針和逆時針的流動,并作方向統一處理,不考慮發生大尺度環流翻轉的過程.

3 二維湍流熱對流Re 數特性

Re數是反映熱對流系統的湍流流動特性的特征參數.本文研究系列Pr數及Ra數下的二維RB 系統湍流Re數與Ra數和Pr數之間的變化規律及特性.

圖2 給出了一個典型流態的平均速度場云圖.圖2 可見,該速度分布成圓環狀,方腔四個角落中的速度都較小,速度分布在中心速度很小,隨著半徑的變化速度快速增大,到接近一半的位置速度達到最大,而后速度隨半徑的增大速度減小.

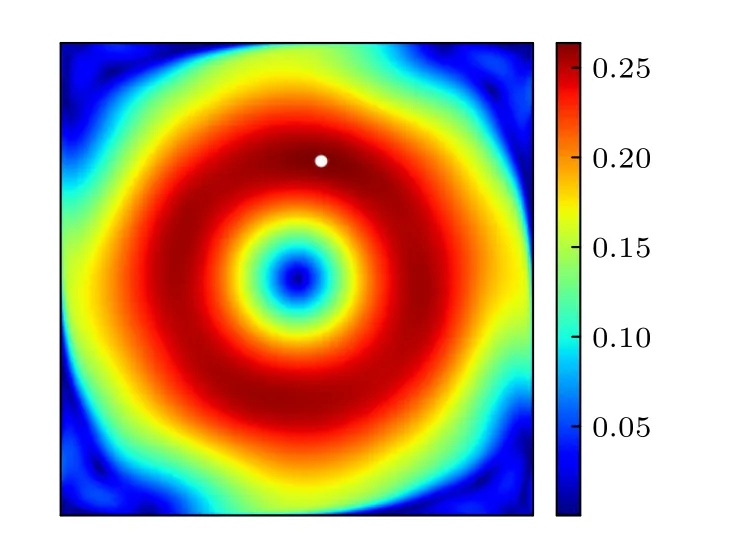
圖2 平均速度分布及最大速度點Fig.2.The time-averaged velocity filed and the maximum velocity point.

經過計算全場的速度大小,找到絕對速度的最大值,即圖2 中白點處的速度,作為計算湍流熱對流Re數的特征速度,其無量綱的計算公式如下:

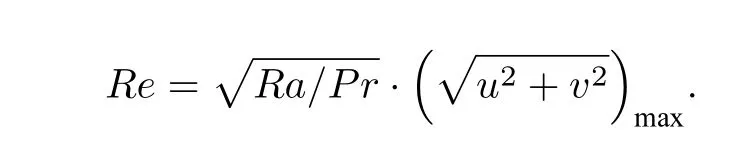
3.1 二維湍流熱對流Re 數變化規律及其間斷特征

首先,以Pr=0.7的系列Ra數熱對流為典型計算結果,探討熱對流的Re數隨Ra數的變化規律.

圖3 給出了Pr=0.7的系列Ra數熱對流的Re數隨Ra數的變化情況,圖中為雙對數坐標.可以看到,Re數隨Ra數的增加逐漸增大,表明系統的湍流強度隨Ra數增加逐漸變強.特別地,Re數的變化在Ra=109處出現了間斷平移,分成了較明顯的兩段.

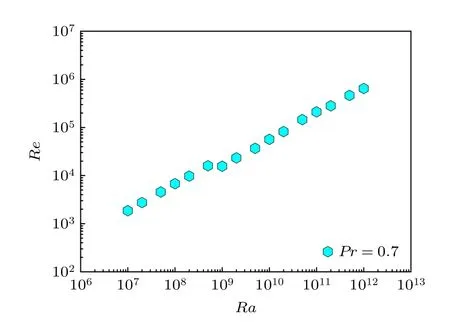
圖3 Re 數與Ra 數關系Fig.3.Re as a function of Ra.

對于Re數與Ra數的變化關系中出現的間斷平移,是由二維湍流熱對流的流態突變造成的,將在下節內容中詳細討論.

3.2 二維湍流熱對流流態突變及最大速度變化特性

在低Ra數時,二維湍流熱對流的流態是傾斜的橢圓大尺度環流加兩個角渦的流態.隨Ra數增高,角渦會發生脫離導致流動失穩,系統的流態突變成圓形的大尺度環流流態[19].

圖4 給出了Pr=0.7 時流態從橢圓突變成圓形前后典型流態的平均速度場云圖,圖中明顯可見兩種完全不同的速度分布.由于不同Ra數時速度值得變化范圍較大,為了清楚地反映速度分布情況,每個Ra數對應的速度云圖色標范圍是不一致的,均設置為各個算例的最小速度到最大速度.在Ra數較低的圖4(a)和(b)中,速度分布形態基本一致,均為傾斜的橢圓形和兩個角渦,圖中白點為最大速度點,都出現在橢圓和角渦的相切處.大尺度環流與角渦相切的位置速度都會比較大,而接近另外兩個角落的速度較小.隨著Ra數增高,Ra=1×109時流態發生突變,大尺度環流形態突變為圓形,如圖4(c)和(d)所示.突變后高速區域呈圓環狀,整體速度相近,最大速度隨機產生在圓環上,并且最大速度相較突變前略有減小,這一點在圖4的色標范圍上可以看出.

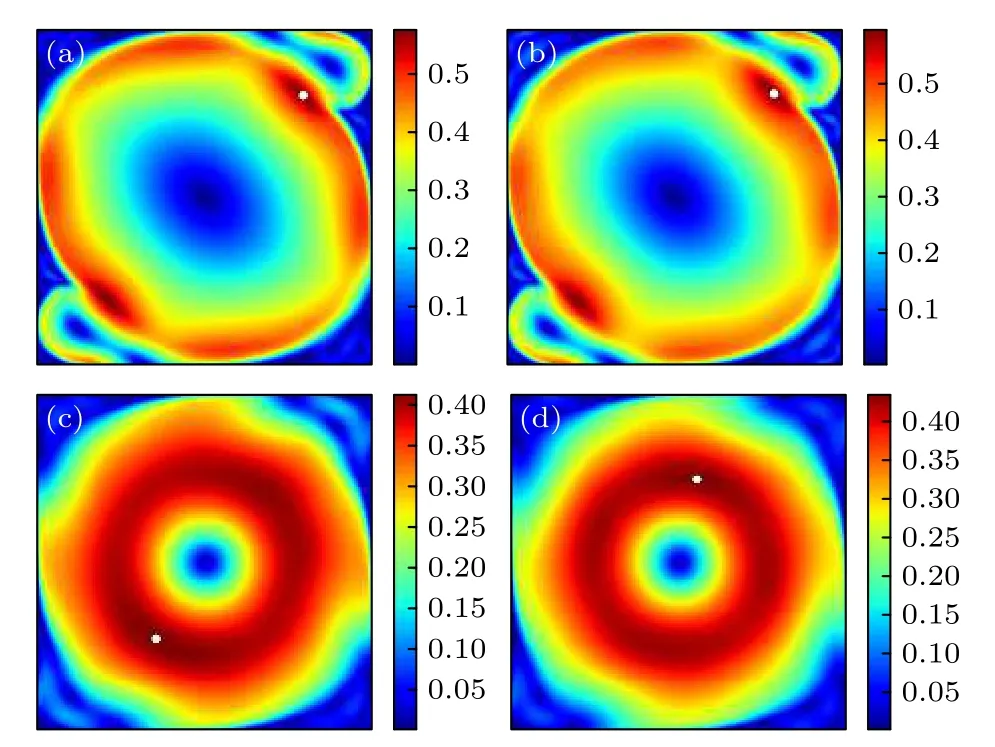
圖4 平均速度場變化及流態突變(Pr=0.7) (a) Ra=2×108;(b) Ra=5×108;(c) Ra=1×109;(d) Ra=2×109Fig.4.The time-averaged velocity fieldsc and the sudden change of flow pattern (Pr=0.7): (a) Ra=2×108;(b) Ra=5×108;(c) Ra=1×109;(d) Ra=2×109.

計算Pr=0.7 時所有Ra數情況下的最大速度值,探討最大速度值隨Ra數的變化規律.

圖5 給出了Pr=0.7 時不同Ra數的平均速度場中最大速度值Umax隨Ra數的變化情況.可以看到,最大速度的變化明顯分為兩段.當Ra≤5×108,大尺度環流流態為橢圓,隨著Ra數的提高平均速度場中的最大值Umax逐漸變大.在Ra=1×109時,大尺度環流流態突變為圓形,最大速度Umax間斷式突然下降.之后隨著Ra數增大,平均速度場中的最大值Umax再次逐漸變大.當Ra≥5×1010后,最大速度Umax出現波動,但速度值變化不大.

二維湍流熱對流在較低Ra數時呈橢圓形大尺度環流形態,由于羽流基本沿橢圓路徑運動,流動相對集中穩定,使平均場速度較大.隨著Ra數的提高,速度增大,帶動角渦脫落造成流態失穩混亂,導致流態從橢圓到圓形的突變[31].當流態失穩突變后,羽流運動呈現較為混亂的繞行,會使平均后的速度場整體減小,所以導致圖5 中最大速度間斷式減小.

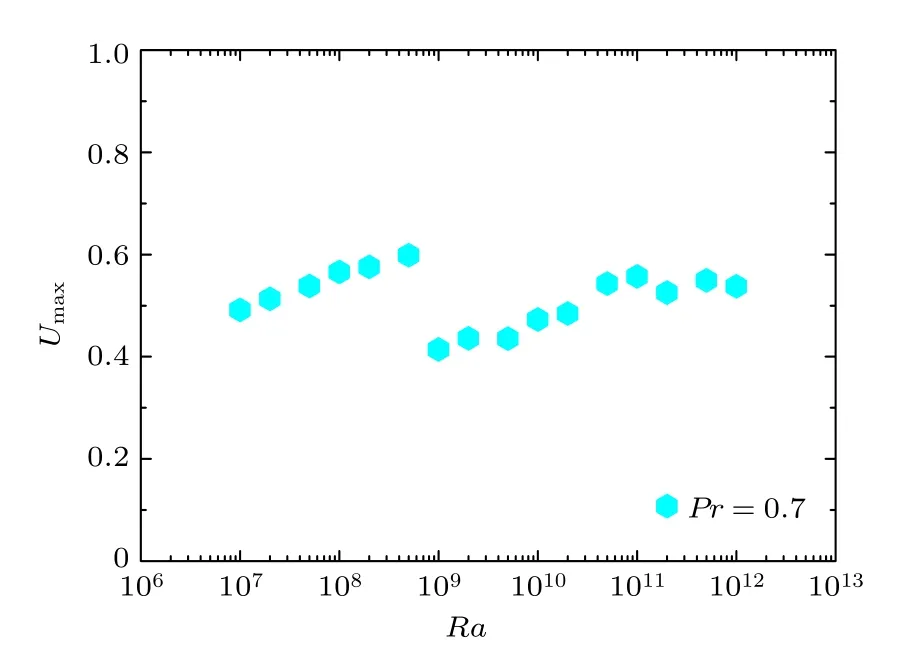
圖5 最大速度隨Ra 數變化Fig.5.The maximum velocity as a function of Ra.

熱對流在流態突變時平均場最大速度Umax的間斷式減小,是造成圖3 中Re數隨Ra數的變化規律出現間斷的原因.

4 不同Pr 數的Re 數規律及臨界Re 數

本文計算了10 個不同的Pr數系列的算例,數據較多.為清晰展示結果,在討論二維湍流熱對流Re數特性的Pr數影響時,首先選取3 個典型的Pr數0.7,4.3 和10 進行分析.

圖6 給出了3 個Pr數系列的Re數的變化特性,藍色六邊形、紅色方形和綠色實心圓點分別為Pr=0.7,4.3 和10,黑色線表示 1.4×104.由圖6 中可見,3 個Pr數系列的Re數都分別隨Ra數的增大而增大,同時Re數隨Ra數分布有兩個階段,階段之間存在明顯的間斷.將間斷處的Re數定義為流態突變特征Re數Rec,Ra數定義為流態突變特征Ra數Rac.有意思的是,不同Pr數時流態突變對應的特征Re數Rec的值基本一致(Rec≈1.4×104).也即,無論Pr數為多少,當Re數達到Rec時,平均場的大尺度環流形態一定會從橢圓形突變為圓形.

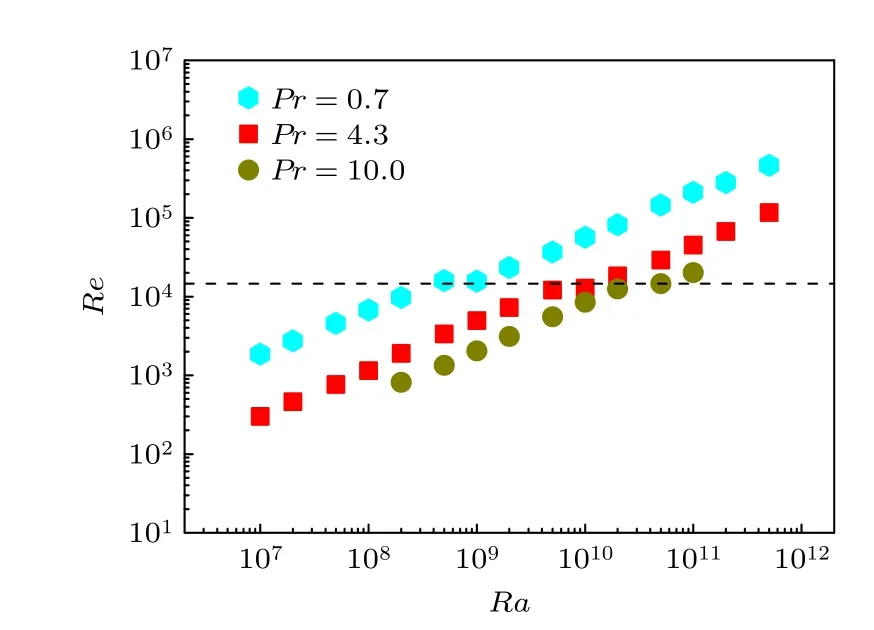
圖6 Re 數與Ra的關系圖Fig.6.Re as a function of Ra.

這一現象的原因與上文討論的Pr=0.7的一樣,是由于最大速度值在流態突變處出現驟減,導致Re數變化出現間斷平移.另外,隨著Pr增大,發生間斷平移的位置會向右移,表明隨Pr增大,Rac會逐步增大.

計算所有Pr數下二維湍流熱對流的Re數,Pr數范圍為0.25—100,討論這個范圍內不同Pr數情況下,熱對流的Re數與Rac的變化規律.

圖7 給出相應的Pr從0.25 到100的系列Ra數下Re數分布.圖中發現不同Pr數下湍流Re數分布特征與之前3 個典型Pr數情況相似.Re數從一百左右到幾十萬,跨度4 個量級.除了Pr=50 和100 時Re數數值不夠大,其他的結果都在流態突變特征Re數處存在間斷,間斷點對應的Ra數依次往后移動.然而間斷處的Re數,也就是流態突變特征Re數的值基本相同,是一個常數,Rec≈1.4×104.也即,對于不同系列Pr數和Ra數,當由最大速度定義的Re數達到特征Rec時,流態就會發生由橢圓型大尺度環流到圓形大尺度環流的流態突變,流體突變特征Re數Rec與Pr數和Ra數變化無關.

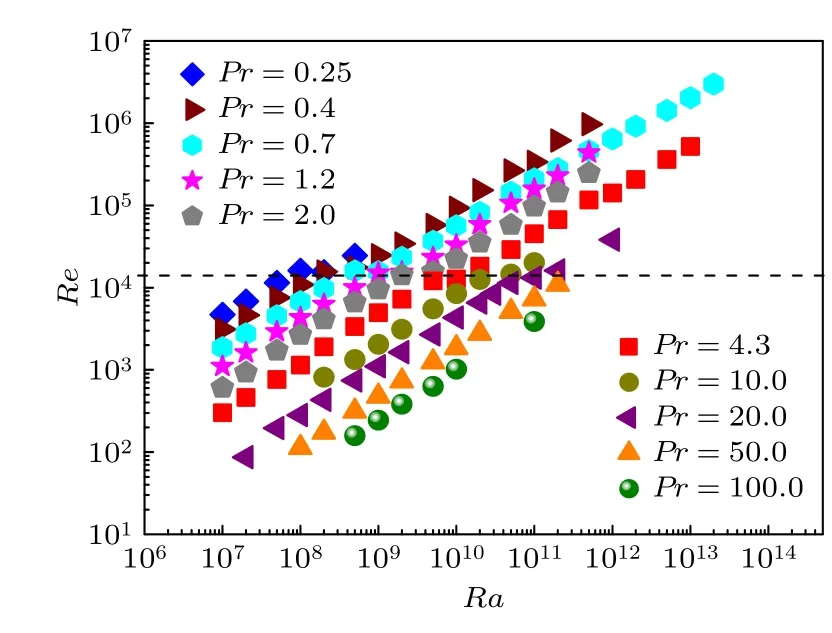
圖7 不同Pr 數下Re 數與Ra 數的關系Fig.7.Re as a function of Ra at different Pr.

在不同Pr數下,Rac的位置逐漸右移,表明Rac隨Pr增大而增大.在二維RB 熱對流中,流態突變Ra數與Pr數有Ra-Pr1.5的標度律關系[30].為了探討不同Pr數下Re數的轉變共同特征,對橫坐標Ra數進行補償平移,研究Re與RaPr—1.5的關系.

圖8 給出Re數隨RaPr—1.5的分布.圖中可見,10 個Pr數的Re(RaPr—1.5)分布完全重合在一起,表明在不同Pr數下,Re數的變化規律基本一致,呈現很好的自似性.

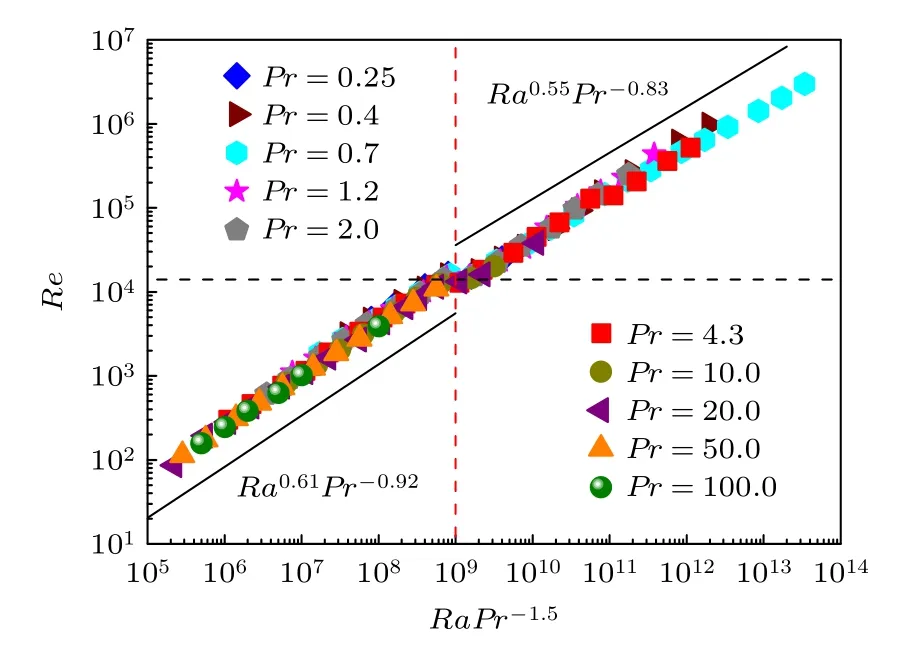
圖8 不同Pr 數下Re 數與RaPr—1.5的關系Fig.8.Re as a function of RaPr—1.5 at different Pr.

圖8 中黑色虛線表示Rec≈1.4×104,紅色虛線表示RacPr?1.5=109.兩條虛線的交點對應不同Pr數下的流態突變.這表明不同Pr數都有基本相同的流態突變特征點位置,RacPr?1.5=109,同時Re=Rec≈1.4×104.這是兩個常數,可以用于預測不同Pr數和Ra數下流態發生突變的時機以及系統Re數的變化趨勢,對區分不同參數下的流態以及流態突變特性的探討有重要意義.當RaPr?1.5＜109時,系統的流態為橢圓形;當RaPr?1.5=109時,系統的流態會發生突變,系統的Re數達到Rec≈1.4×104;隨后RaPr?1.5＞109,系統的流態為圓形.

另外,對圖8 中所有數據進行Re-(RaPr—1.5)γ的擬合,得出: 流態突變前,Re數的標度律為Re-Ra0.61Pr—0.92,流態突變后為Re-Ra0.55Pr—0.83.

流態突變的臨界Re數為常數,反映出二維湍流熱對流特殊的流動形態變化特征,也將為二維湍流熱對流的流動特性研究以及對應的傳熱特性變化特征等問題的研究提供新的思路.更多的價值還需要進一步深入的研究.

5 結論

本文采用高效并行直接求解計算方法PDMDNS 完成了系列Pr數和Ra數的二維湍流熱對流的DNS 模擬,Pr數從0.25 到100,Ra數從1×107到1×1012,跨度為5 個量級,總共133 個計算算例,所呈現的結果是目前二維湍流熱對流系統相當完整的數據.本文研究以平均場最大速度為特征速度的Re數特性以及最大速度的變化規律,發現大尺度環流形態由橢圓形變為圓形的突變對Re數特性的影響.研究結論如下:

1)典型算例Pr=0.7 時的Re數特性結果表明,Re隨Ra數的變化存在標度律關系,但中間出現明顯的間斷現象.從基本流態特征出發進行研究發現,大尺度環流形態由橢圓形突變為圓形會引起最大速度值的間斷式突然下降,導致Re數特性的間斷現象出現.

2)不同Pr數的Re數特性研究表明,Re數隨Ra數的變化特性有明顯的自相似性.并且發現,流態突變對應的特征Re數Rec為常數,與Pr數和Ra數變化無關,Rec≈1.4×104.當Re數達到特征Rec時,大尺度環流形態會發生突變,從橢圓形變為圓形.這為RB 熱對流的流態區分提供新的方法,并且進一步根據Re數的自相似性進一步預測Re數的變化規律.

3)流態突變特征Ra數Rac與Pr數之間存在標度關系Rac-Pr1.5.對橫坐標Ra數進行補償平移,Re與RaPr—1.5的變化曲線完全重合,表明不同Pr數時Re數隨Ra數的變化規律基本一致,流態突變前后分別有Re-Ra0.61Pr—0.92和Re-Ra0.55Pr—0.83的標度律關系.不同Pr數有基本相同的間斷特征點位置,RacPr?1.5=109.