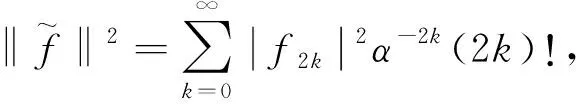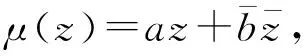Toeplitz算子的雙正規性和M-亞正規性

崔璞玉, 李 佳, 馮琳穎

(遼寧師范大學 數學學院，遼寧 大連 116029)

算子理論中正規算子的研究已經非常完備. 特別地, Toeplitz算子的正規性也有較完全的描述, 許多學者將正規性的概念推廣得到擬正規性、M-亞正規性、雙正規性等.

設H為無窮維復可分Hilbert空間,B(H)為H上一切有界線性算子所構成的Banach代數.T*表示T∈B(H)的共軛算子.如果T*T=TT*, 則T是正規的; 如果T*TT=TT*T, 則T是擬正規的; 如果T*TTT*=TT*T*T, 則T是雙正規的; 若存在M>0, 使得對于所有的ω∈,f∈H有‖(T-ω)*f‖≤M‖(T-ω)f‖成立, 則稱T是M-亞正規的.

在相關的文獻[1-17]中, 可以看出大多是在Hilbert空間上研究雙正規和M-亞正規算子的性質等相關內容, 在具體函數空間如Bergman空間和Fock空間上關于雙正規和M-亞正規Toeplitz算子的符號特征的研究相對較少.

令η表示[0,1]上的概率測度.定義開單位圓盤上的測度v為記()為上的加權Bergman空間, 是由L2(,dv)中所有解析函數構成的空間, 顯然有()是L2(,dv)的閉子空間.定義集合{τt}t∈[0,∞)為

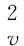
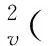
則其上的內積可以表示成

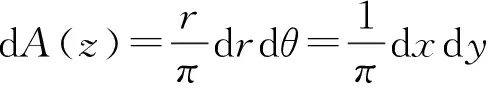
Tφ(f)=PB(φf),

其中,PB是從L2(,dv)到()的正交投影.

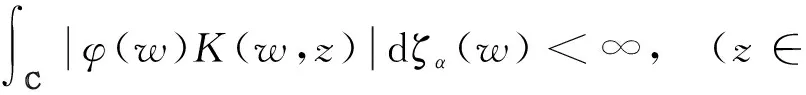
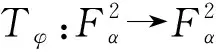
PF是從L2(,dζα)到的正交投影.

1 Bergman空間上Toeplitz算子的雙正規性

定理1.1設φ(z)=eikθf(r)∈L∞(,dv), 其中,z=reiθ,k∈,f(r)是一個有界徑向函數.Tφ為上擬正規的當且僅當滿足以下條件:

(1)k<0,f=0;

(2)k=0;

(3)k>0, 且對任意n∈, 或者有f=0, 或者

證對任意n∈, 有

直接計算可以得到

另一方面,

設k<0, 當-k≤n<-2k時, 有

如果Tφ是擬正規的, 則有

(1)

當n≥-2k時, 有

如果Tφ是擬正規的, 則

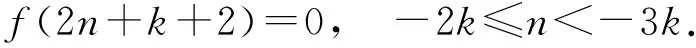
(2)

以此類推, 對任意n≥-k, 有

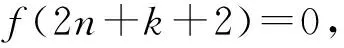
(3)

由式(3)可知f=0.

設k=0, 易得Tφ是正規的, 顯然Tφ是擬正規的.

設k>0, 對任意n∈,

如果Tφ是擬正規的, 當且僅當

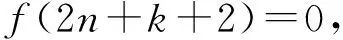
利用定理1.1中的方法可直接得到定理1.2.

定理1.2設φ(z)=eikθf(r)∈L∞(,dv), 其中，z=reiθ,k∈,f(r)是一個有界徑向函數.Tφ在上是雙正規的.

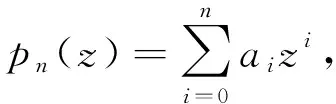
(1)n=0;

(2)n>0且a0=a1=…=an-1=0.

證首先證明充分性.若pn(z)=anzn, 則Tpn是單邊加權移位算子, 則其一定是雙正規的.

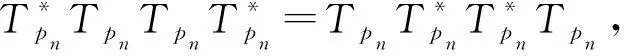
同樣地，

對比上述兩個多項式中z2n-1項的系數:

由此可見a0=0或a1=0.當a0≠0時, 繼續依次對比各項系數

由此可見a1=a2=…=an=0與an≠0矛盾.

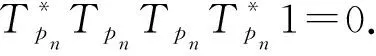
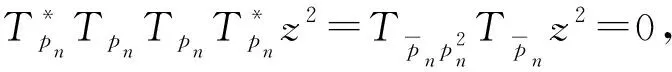
而

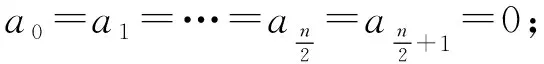
為了給出Bergman內函數與雙正規Toeplitz算子之間的關系, 下面給出一個關于Bergman內函數的引理.

引理1.4設pn(z)=anzn+an-1zn-1+…+a0, 其中，n≥1,an≠0.則pn(z)為Bergman內函數當且僅當

證只需證必要性, 若pn(z)為Bergman內函數, 那么對任意zk,k≥1,〈pn(z),pn(z)zk〉=0.由計算可得

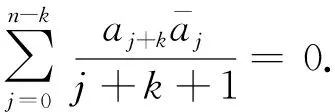
結合定理1.3和引理1.4可以得到下面的推論:

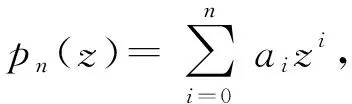
2 加權Bergman空間和Fock空間上Toeplitz算子的M-亞正規性

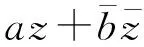
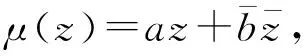
取f0=1,f1=0, 得

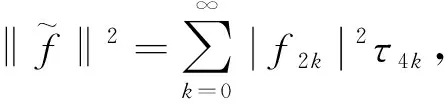
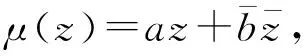
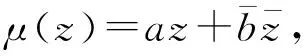
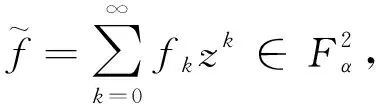
取f0=1,f1=0, 得