基于親和矩陣塊對角性的子空間聚類

唐科威， 林 棟， 張 楠

(遼寧師范大學 數學學院，遼寧 大連 116029)

進入“大數據”時代，各行業的數據量呈現爆炸式增長，如教育、醫療、交通、餐飲、電商等領域每天都有大量數據產生.為了有效地處理這些海量數據，數據的本質幾何結構分析一致備受關注，文獻[1]指出，一個人在不同光照下的人臉圖像位于一個低維子空間中.由于實際問題中的數據往往包含多個類，子空間聚類問題被提出.子空間聚類是指將給定的取自多個子空間并集的數據點劃分到各自對應的潛在子空間中.

在過去的20多年內，專家學者們提出了許多子空間聚類的算法[2]，例如：迭代方法[3]、因子分解方法[4]、統計方法[5]和基于譜聚類的方法.其中，基于譜聚類的方法在近幾年引起了廣泛的討論[6].這類方法首先是要構造一個親和矩陣來表示數據點之間的相似性，然后利用譜聚類算法作用于親和矩陣上得到子空間聚類結果.通常使用的譜聚類算法是Normalized Cut(NC)[7].因此，對于親和矩陣，如果能將同類數據點間的相似性構建的相對大, 不同類數據點間的相似性構建的相對小，往往能獲得更加準確的聚類結果.對于兩個經典的基于譜聚類的算法，低秩表示Low-Rank Representation (LRR)[8]和稀疏子空間聚類Sparse Subspace Clustering(SSC)[9]都采用了原始數據自表示來提取數據之間的關系，即

X=XZ.

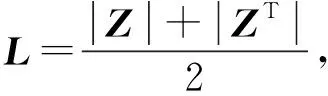
文獻[10]詳細地分析了上述塊對角性質，給出了引入塊對角懲罰的方法，同時提出了基于塊對角劃分的子空間聚類方法Block Diagonal Representation(BDR).BDR通過使用塊對角正則項使得表示系數矩陣是塊對角的.但是，為了便于求解，塊對角正則項的使用有著一定的條件，即需要對施加塊對角懲罰的矩陣加以非負與對稱的限制.體現在BDR中，就是需要對表示系數矩陣加以非負與對稱的限制.基于這類方法的原理和流程，不難發現這種做法會在一定程度上限制表示系數矩陣挖掘數據之間關系的能力，BDR文章中也承認了這一點.具體地說：一部分數據點被某一部分同類數據點線性表示時，表示系數必然是負的，如果限制表示系數矩陣非負將無法挖掘出它們之間的關系.下面用人造數據為例進行說明，在3維空間中，隨機生成3條過原點的直線，并在每條直線上，任取了100個點進行試驗，這是一個三類問題.發現BDR并不能正確聚類，結果如圖1(a)所示.

圖1 利用人造數據，分別在BDR和本文的方法進行實驗(a)BDR的聚類效果圖；(b)本文的方法的聚類效果圖；(c) BDR的親和矩陣圖；(d)本文方法的親和矩陣圖Fig.1 The experimental results of our method and BDR on synthetic data(a) The clustering result of BDR；(b) The clustering result of our method；(c) The affinity matrix of BDR；(d) The affinity matrix of our method

BDR不能正確聚類的原因如下：在原點兩側，同一條直線上的數據點在互相線性表示時表示系數必然是負的，而BDR對表示系數矩陣有著非負的限制，這使得BDR無法挖掘出它們之間的關系，這從BDR的親和矩陣上可以看出，圖1(c)中的親和矩陣有6個對角塊而不是3個.其實，從這類方法的流程和原理上可以發現，對表示系數矩陣塊對角性的追求無非是為了保證親和矩陣的塊對角性，而親和矩陣必然是非負和對稱的.為了解決BDR中的問題，對親和矩陣考慮塊對角先驗提出基于親和矩陣塊對角性的子空間聚類方法.該方法對親和矩陣進行了塊對角懲罰，相對于BDR，這里的方法不僅能避免限制表示系數矩陣的表示能力，而且能同樣保證親和矩陣的塊對角性，從而提高聚類性能.圖1(b)和圖1(d)說明了該方法思路的正確性.但是親和矩陣與表示系數矩陣具有非線性的運算關系，在目標函數中對親和矩陣進行懲罰會帶來模型求解上的困難.幸運的是，發現使用交替方向迭代法Alternating Direction Method(ADM)可以有效地求解模型.最后，在多個數據集上的大量實驗表明了方法的有效性.總之，本文的貢獻如下：

(1)提出了基于親和矩陣塊對角性的子空間聚類方法，該方法可以在一定程度上克服BDR方法的局限性.

(2)以往工作都是在目標函數中對表示系數矩陣進行懲罰,而本文則是采用了對親和矩陣進行懲罰的策略，這是一種全新的嘗試.雖然這種做法會帶來求解上的一些困難，但是給出了有效的數值算法.

(3)在多個數據集上的實驗證實了本文方法是一個有效的子空間聚類方法.

1 相關工作

1.1 符號說明

1.2 回顧BDR

表示系數矩陣塊對角性對于子空間聚類起著不可或缺的作用，為了便于對下文理解，本文首先回顧BDR子空間聚類中的以下定義.

定義1[10](k塊對角矩陣) 對于任意的B∈n×n如果它有k個連通塊，那么就稱它為k塊對角矩陣.

例如：圖1(c)中，它有6個連通塊，則稱它為6塊對角矩陣，同理,圖1(d)稱為3塊對角矩陣.

如果B是一個滿足B≥0且B=BT的矩陣，則對應的拉普拉斯矩陣LB定義為

LB=diag(B1)-B.

這里LB是一個半正定矩陣.

引理1[10]對于任意矩陣B,如果滿足B≥0且B=BT，則拉普拉斯矩陣LB特征值0的重數k等于B中連通塊的數量.

那么對于任意的矩陣B∈n×n，如果滿足B≥0且B=BT，根據引理1，B是k塊對角矩陣當且僅當

其中，λi(LB),i=1,…,n.為LB從大到小的n個特征值.基于這樣的性質，可以定義k塊對角正則項如下：

定義2(k塊對角正則項)[10]對于任意滿足非負和對稱的矩陣B∈n×n，k塊對角正則項定義為LB最小k個特征值的和，即

當矩陣B是k塊對角的，則‖B‖k=0.相反，如果‖B‖k=0，矩陣B至少有k個連通塊.因此,‖B‖k可以看作是塊對角矩陣結構誘導的正則項.所以BDR子空間聚類的模型：

(1)

其中，X∈d×n是從k個子空間的并集中提取的數據矩陣，X的每一列代表一個數據點.B∈n×n是表示系數矩陣，γ是平衡不同項的參數.為了誘導塊對角結構，模型(1)不得不對表示系數矩陣B加了非負且對稱的限制條件，這會限制表示系數矩陣挖掘數據之間關系的能力.BDR文章中也說明了該局限性.

2 模型求解

2.1 本文模型

對表示系數矩陣誘導塊對角結構本質上是為了對親和矩陣誘導塊對角結構，而親和矩陣必然是對稱和非負的.為了克服BDR的局限性.這里做出一次大膽的嘗試，選擇對親和矩陣使用k塊對角正則項.

(2)

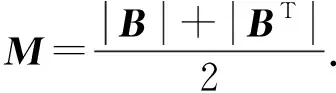
2.2 數值算法

使用ADM方法求解模型，為此，引入輔助變量Z則有：

則模型(2)的增廣拉格朗日函數為

(3)

下面利用BDR中的引理處理‖M‖k.

引理2(1)http:∥meboo.convexoptimization.com/Meboo.html如果L∈n×n并且L0那么

根據式(3)，最終模型的求解可以歸結為3個子問題的討論：

對于變量B:

通過推導得出

〈LM,W〉=tr((diag(M1)-M)W)=tr(MT(diag(W)1T-W)).

(4)

(5)

注意模型(5)無法直接使用軟閾值算子，因為矩陣V中的元素可能是負的，通過推導得到該問題更新方案為

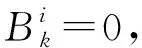
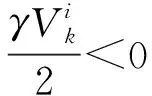
其中,i,k=1,…,n.

(6)

對于變量W：

利用式(4)，將求解W的問題轉化為求解下式

利用BDR中對W的處理方式，知道該子問題有解W=QQT,其中，Q是diag(M1)-M的k個最小的特征值的特征向量.

對于變量Z：

解為

Z=(XTX+μI)-1(XTX+μB-Y).

(7)

最后，文章的算法總結如下:

算法 1 利用ADM算法求解模型(2)輸入:數據矩陣X和參數γ,k.輸出:表示系數矩陣B.初始化:B=Z=0,W=0,Y=0,μ=10-6,tol=10-4.步驟1:固定其他參數按照式(7)更新Z.步驟2:固定其他參數更新B, 當i=k時,則Bik=0,如果i≠k,則按照式(6)更新Bik.步驟3:固定其他參數更新W,即W=QQT,這里Q是diag(M1)-M的k個最小的特征值的特征向量,其中,M=B+BT2.步驟4:更新乘子Y=Y+μ(Z-B).步驟5:更新μ=min(1.1μ,1030).步驟6:檢驗收斂條件:‖Z-B‖∞

3 實 驗

在本節中，在人造數據、COIL-100(2)http://www1.cs.columbia.edu/CAVE/software/softlib/coil-100.php、USC SIPI 紋理庫、MNIST數據庫[11]上進行了幾組實驗來證明方法(記為OUR)的有效性.并與SCC[12]、SSC[9]、LRR[8]、LSR[13]、BDR-B和BDR-Z[8]方法進行比較.在以上3個數據庫中，分別針對不同的聚類方法調整參數，為每種方法在其3個數據庫中找到最優的參數.為了降低數據的維度，采取預處理的方式對數據進行有效的降維.

3.1 人造數據

為了直觀的對比本文方法的優越性，在3維空間中，隨機生成3條過原點的直線，并在每條直線上，任取了100個點進行實驗.實驗結果如圖1，發現由于BDR對表示系數矩陣加了非負和對稱的懲罰，所以在原點兩側它并不能得出正確的聚類結果，如圖1(a).并且通過觀察親和矩陣的圖1(c)也可以看出，它的分類數是6而不是3，顯然錯誤.而本文的方法是利用親和矩陣的非負和對稱性，通過圖1(b)和圖1(d)可以看出本文的方法能得到正確的聚類.

3.2 COIL-100

該數據集包含了100個不同物體的7 200張灰度圖像, 其中，每個物體包含72幅圖像.每幅圖像的大小是128×128.從中選取10類圖形，每類取50張進行實驗.正確率見表1.

表1 每種方法在 COIL-100上的正確率Table 1 The accuracy for each method on coil-100 %

3.3 USC SIPI 紋理庫

本文的方法對于 USC SIPI 紋理庫的實驗也可以得到比較好的結果.USC-SIPI 紋理庫包含13種紋理，每種紋理又包含7種不同角度狀態.實驗中隨機選取了5類紋理，每類紋理全部圖像在所有角度下的數據，所以共有560幅圖像.正確率見表2.

表2 每種方法在USC SIPI紋理庫上的正確率Table 2 The accuracy for each method on USC SIPI %

3.4 MNIST數據庫

旋轉的MNIST數據庫包含大小為28×28像素的手寫數字的灰度圖像.圖像最初取自文獻[14]中引入的MNIST數據集，并通過幾種方式進行了轉換，以產生更具挑戰性的分類問題.本文選取后三類作為實驗對象，每類200張.

表3 每種方法在MNIST數據庫上的正確率Table 3 The accuracy for each method on MNIST %

4 結 論

本文提出了基于親和矩陣塊對角性的子空間聚類方法，在原有BDR子空間聚類模型的基礎上做了改進，本文的方法不需要限制表示系數矩陣非負或者對稱.同時本文的方法直接對親和矩陣進行塊對角懲罰，這也是一種全新的嘗試，具有重要意義.最后，各種基準數據庫上的大量實驗結果表明了本文算法的有效性.