一般壟斷下廠商最優和社會最優的動態優化比較

宋建朋 鐘根元 陳志洪

(上海交通大學 安泰經濟與管理學院，上海 200030)

0 引言

隨著社會生產力的發展和人民生活水平的提高，消費者對商品的購買力也在不斷提高。這為制造業廠商帶來了更大的市場，同時也對商品質量和性價比提出了更高的要求。廠商如何進行生產決策，來獲得更高的收益、耗費更小的成本是一個值得研究的問題。一方面，一種商品的競爭力越來越多地依賴消費者對其質量、功能、商譽、售后服務等諸多因素的評價，而這些因素的提高，需要企業持續進行技術創新投入；另一方面，通過改進生產技術、科學地進行生產管理，即過程創新，企業可以顯著降低商品的生產成本。這兩種方式都可以增加企業的生產者剩余，是市場經濟中提高企業利潤的重要手段。每個創新型企業都會兼顧這兩方面的投資，而協調這兩方面的投入，使得企業利潤或社會福利達到最大化，本質上是一個動態優化的問題。

由于研究方法和模型的差異，長時間以來，研究人員對于兩種創新方式的關系有比較大的爭論。早期，Utterback和Abernathy(1975)研究了一個企業在特定生產過程的發展狀態和其選擇的競爭模式下產品創新和過程創新之間的關系。Martinez(1999)、Mantovani(2006)等人的研究表明產品創新和過程創新之間存在互補的關系。但并不是所有的研究都支持這一觀點，Lanbertini和Orsini(2015)認為企業是獨立進行產品創新和過程創新投入決策的。Rosenkranz(2003)的研究表明，在競爭強度較低時，企業只會采取產品創新，而Weiss(2003)卻提出了相反的看法，他認為在競爭強度較高時，企業會有逃離競爭的激勵，去投入產品創新。Adner和Levinthal(2001)指出企業會根據市場特征決定如何投入產品創新和過程創新。

隨著動態模型研究的不斷深入，越來越多的決策因素和市場模型正在被廣泛研究。Becker和Egger(2013)研究了技術創新和過程創新對企業出口傾向的影響；Lanbertini和Mantovani(2009)研究了多產品壟斷廠商的產品、過程創新的互補關系；Hasnas、Lambertini和Palestini(2014)研究了開放式創新環境中寡頭企業的決策；Zhong和Zhang(2017)研究了企業對產品創新、過程創新投入與知識積累和折舊的關系。

雖然目前研究人員關于產品創新和過程創新已經有了很多的發現，但是很少有文章會涉及企業最優決策的定量研究，而最優決策的定量研究無疑可以給合理決策提供很有說服力的參考。所以，本文在保留傳統研究內容的基礎上，希望通過求解最優決策表達式，給決策方提供更加精確的參考和幫助，并且結合決策路徑的表達式，直觀地分析一些因素對于決策的影響。總結來說，本文的主要貢獻在于：(1)求解出一般壟斷市場下企業最優和社會最優時的廠商決策最優路徑；(2)證明了一般壟斷市場在動態條件下和靜態條件下具有相同的結論，更接近一般實際；(3)考察了利率、企業初始值等因素對企業決策的影響。

本文的第一部分，對廠商最優的生產決策進行了求解，并考察了利率、廠商初始值等一些外生變量對結果的影響；第二部分求解了社會最優時的生產決策，并對兩者進行了對比，得到了與靜態模型相同的結論，證明了動態過程是靜態模型更接近實際的推廣；第三部分討論了利率和變量的初始值對企業決策的影響。

1 一般壟斷廠商最優決策

根據Pan和li(2016)關于商品需求的理論，商品的銷量隨著質量的提高而增加。商品的質量越高，消費者對它的評價就越高，需求就會越高。據此可以假設反需求函數具有如下形式：

p=a1+a2q-a3x

(1)

在這里，本文只引入了一個質量變量來影響價格，而在實際市場中，可能存在很多影響價格的因素，如商譽或是售后服務等。零售商可以通過廣告等營銷手段提高它的商譽，或是通過具有吸引力的售后服務來吸引消費者。這些措施都可以提高產品的市場需求，并且它們之間可能存在互補或是替代關系。但這些策略的研究方法和結論是類似的，為了簡化模型，本文只引入一個質量變量，并且設它和需求的關系為線性。

根據Lanbertini和Orsini(2015)的理論，對于企業來說，可以通過投入產品創新，以提高產品的科技含量、功能或是感官體驗來提高消費者對產品的評價。但隨著時間的推移，新技術的產生使得這些因素變得不那么流行，類似于一種質量“折舊”。所以，企業的產品創新變化由下式決定：

q=k1-δq

(2)

其中，k1是廠商的產品創新投入。另一方面，企業通過過程創新來降低平均成本，帶來更多的生產者剩余。但企業的生產成本也會隨著設備的老化等問題隨時間逐漸上升，所以生產成本的變化函數為：

c=-k2-ηc

(3)

式中，k2是廠商的過程創新投入。企業投入技術創新和過程創新所帶來的成本是：

(4)

成本正比于技術投入水平的二次方，是因為這兩項投入帶來的邊際收益是遞減的。對于一個特定的廠商，給定決策變量產品創新投入k1、過程創新投入k2、狀態變量質量q、生產成本c的初始值k10、k20、q0和c0，模型的最決策優路徑就固定下來。接下來對變量的路徑進行求解。

企業每個時期的利潤為銷售額減去生產成本和創新的投入成本：

(5)

設利率為r(t),為了簡化模型，可以假設利率在較長時間內保持穩定，即r(t)=r,由Chenavaz(2012)關于企業利潤流最大化要求的研究可知：

(6)

所以，當期漢密爾頓函數為：

(7)

根據最優化的一階條件，以及乘子方程可以列出：

(8)

聯立此微分方程組和式(2)、(3)，得到一個七元的一階線性非齊次微分方程組。其中，未知數為控制變量k1、k2、x，狀態變量q、c和共態變量m1、m2。而a1、a2、a3、α、β、δ、η是常數，其數值可以根據行業的統計信息求得。

利用常數變異法進行推導，可以得到控制變量和狀態變量的最終解為

其中，k10、k20、q0、c0是對應變量的初始值，λ、f、g分別由式(10)～(13)決定：

μ1λ4+μ2λ3+μ3λ2+μ4λ+μ5=0

(9)

參數部分的含義如下：

(10)

(11)

(12)

將q和x代入式(1)得到價格的表達式為：

(13)

為了簡化過于復雜的表達式及結果，可以將解析式里的常數取一些典型的數值。如前文所述，數值的選取取決于具體行業的統計數據，參考Lambertini和Mantovani(2009)、Hatch和Mowery(1998)、嚴海寧和朱勁松(2008)的研究成果得到表1的數據:

表1 數值計算的參數取值

取變量的初始值均為0.01，得到：f=0.2724，g=1.1642

結論1：廠商最優的條件下，模型的解存在一個具有穩定性的鞍點均衡。

由式(9)，代入數據后，利用matlab求解得的四個值為：

λ1=0.1000+0.5907i

λ2=0.1000+0.5907i

λ3=0.2630+0.0000i

λ4=-0.0630+0.0000i

因為只存在一個具有負實部的解，說明在此情況下，企業存在一個鞍點均衡。但是解的情況依賴于參數的選取，當參數變化時，需要代入此式求解進行穩定性的驗證。

根據上文所述的過程，得到了控制變量、決策變量關于時間的完整表達式，據此畫出變量路徑的圖像(見圖1～6)：

圖1 產品創新最優路徑

圖2 過程創新最優路徑

圖3 產量最優路徑

圖4 產品價格最優路徑

可以定義變量在完成95%的改變量時基本達到穩態，也就是圖5中所對應的第48單位時間。

圖5 產品質量最優路徑

結論2：在壟斷廠商最優條件下，廠商對產品創新和過程創新的投入之間存在互補關系。

圖6 產品成本最優路徑

證明：將決策變量對時間求導，得

代入數據得

可以看到，產品創新和過程創新的投入均隨時間而增加，即在最優決策時，隨著產品創新投入的增加，需要搭配更多的過程創新，反之亦然。所以兩種創新方式具有互補效應，與Mantovani(2006)的研究結果相符。進一步地，由

可知在本文的模型條件下，k1、k2的技術替代率為定值，企業對兩種技術創新追加的投資是成比例的。

2 社會最優決策

(14)

列出當期漢密爾頓函數：

(15)

沿用上節的解法，解出變量的最優路徑為

(16)

λ2、f2、g2分別由式(17)～(19)決定:

ρ1λ4+ρ2λ3+ρ3λ2+ρ4λ+ρ5=0

(17)

其中：

(18)

(19)

(20)

代入數據得λ2=-0.064，f2=0.2363，g2=1.1372。

結論3：在動態的一般壟斷市場情況下，社會最優和企業利益最大化具有和靜態模型相同的結論，即社會最優時產品的供給量較高，價格較低，且等于生產成本。證明如下：

將式(16)中x的表達式代入需求函數，得到

p=(c0-g2)eλ2t+g2=c

(21)

即在社會最優條件下，廠商對產品的定價等于成本。代入數據，可以得到價格和產量的路徑，并和廠商利潤最大化做比較(見圖7、8)：

圖7 廠商最優和社會最優的產品數量對比

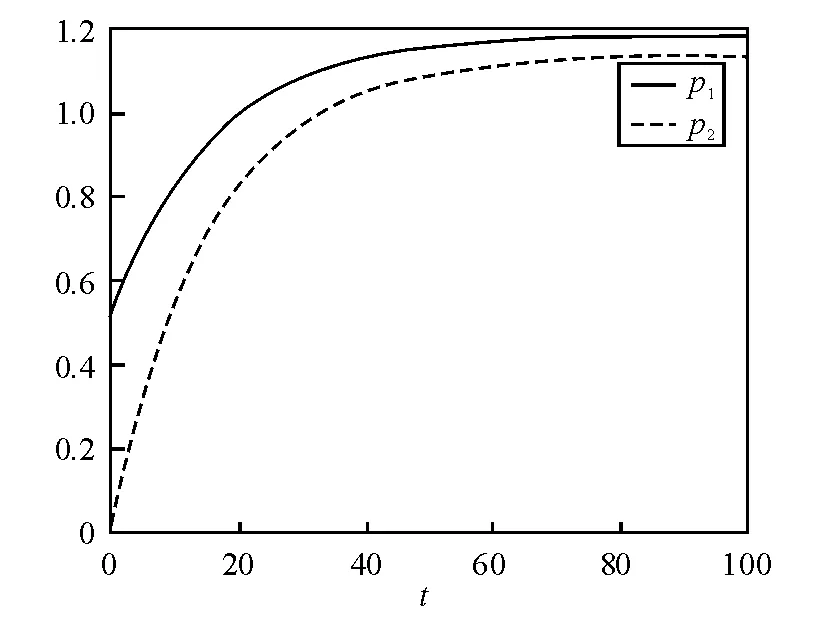
圖8 廠商最優和社會最優的產品價格對比

可以看出，在社會最優條件下，產品的價格更低，產量更高，此時消費者具有更高的福利水平。這和靜態一般壟斷模型的結論是相同的。

3 利率和初始值對決策的影響

決策變量的表達式中折舊和比例常數等參數一般是經濟的外生變量，是企業難以控制并且相對穩定的。利率不僅在很大程度上被政府作為工具來使用，而且對企業的投資決策具有重大影響，所以比較具有研究意義。在本文的模型中，利率不僅影響了企業的利潤水平，同時通過影響λ的值，影響了企業達到穩態的時間：

由式(23)、(24)可求出，為保證穩態時決策變量值為正，即

前文研究了r=0.2水平下的模型，下文通過研究r變化時企業利潤最大化決策中產量和價格的變化，來說明利率對企業決策的影響。利率對企業其他決策、狀態變量也有類似的影響，限于篇幅暫不做討論。

根據式(22)作出r-λ圖像：

由圖9可知，在r從0.12增加的過程中，λ也單調增加，且恒為負，所以產量x和價格p的表達式為

圖9 r-λ關系

結論4：隨著利率絕對值的減少，到達穩態所需時間將會增加，即利率越高，企業決策調整的周期越長。

從經濟學角度直觀地解釋，利率的增加使得投入技術創新資金的機會成本升高，企業將會降低創新力度，緩慢地革新技術。初始值對企業決策的影響，可以從變量的表達式來分析，限于篇幅，本文只討論產品創新和過程創新的初始值對相應企業決策的影響。

由k1的表達式k1=(k10-δf)eλt+δf，可知：

結論5：當k10<δf時，k1會逐漸增加，即企業應逐步增加產品創新的投入。

這是因為產品質量“折舊效應”造成了消費者保留價格下降，它帶來的利潤損失大于企業“節省”的技術投入費用。此時，企業增加過程創新的投入是有利的，因為投入過程創新所帶來的利潤將比技術投入的費用更加可觀。

同理，由k2的表達式k2=(k20-ηg)eλt+ηg，可知：

結論6：當K20<ηg時，企業應該增加過程創新的投入。

與產品創新的原理相同，這是因為過程創新的成本項(資金的機會成本)小于利潤項(成本下降帶來的利潤上升)，所以此時企業需要增加過程創新的投資。

4 總結

本文對具有產品創新和過程創新的一般壟斷市場的動態最優決策進行了求解。與已有的動態模型相比，本文的主要貢獻在于研究方法上的創新。通過求解完整的動態決策路徑，不僅驗證了兩種創新方式的互補關系，得到了和Mantovani等人相同的結論，也比較了社會福利最大化和企業利潤最大化的不同決策，取得了與靜態模型相同的結論，說明動態模型是靜態模型更實際的推廣。同時，作為應用，本文討論了一些參數如利率和變量的初始值對企業決策的影響，這也是目前的動態研究中很少涉及的部分。本文的局限性在于所研究的一般壟斷市場只是一個簡化了的模型，在現實社會中并不常見。在今后的研究將著力對更符合現實的復雜市場模型進行描述和分析求解，以期得到更有價值的發現。