氣墊船導管后支撐振動疲勞影響因素研究

李迎港，郭玉杰，熊宇超，王芳麗，劉磊，印寅

(1.南京航空航天大學 航空學院 飛行器先進設計技術國防重點學科實驗室，江蘇 南京 210016；2.金陵科技學院 機電學院，江蘇 南京 211169；3.航空工業成都飛機工業（集團）有限責任公司，四川 成都 610092)

0 引 言

長期處于振動環境的機械結構，其振動疲勞性能不容忽視。工程結構振動疲勞計算以Dirlik基于蒙特卡羅算法提出的統計模型使用最為廣泛。曹明紅等用多種頻域算法分別計算不同帶寬下結構振動疲勞壽命，并結合實驗結果對比各方法計算精度，結果表明Dirlik 模型普遍使用窄帶響應和寬帶響應，計算精度穩定。王明珠等提出樣本法估算振動疲勞壽命，樣本法是兼顧頻域和時域的算法，計算精度和計算時間隨樣本容量增加而提升。張曉飛等基于頻域譜密度Dirlik 模型對船舶減振支架進行振動疲勞壽命預測，并分析連接剛度對振動疲勞壽命的影響。張翼和羅楊陽等用Dirlik 模型計算導彈吊掛振動疲勞壽命，并從應力響應均方根角度考慮振動疲勞壽命分布規律。黃軍等設計實驗和仿真研究了不同振動譜型對電焊結構振動疲勞壽命的影響，結果表明結構低階固有頻率處的振動激勵對振動疲勞壽命有決定性影響。

本文以全墊升氣墊船空氣導管螺旋槳后支撐為研究對象，主要考慮危險點應力響應和材料疲勞性能對振動疲勞壽命影響，橫向對比各因素對外接頭振動疲勞壽命影響大小，最后結合導管后支撐工作環境和結構特征，對比各優化方案實際可行性。本文較為系統研究了影響振動疲勞的諸多因素，同時提出薄壁結構提高振動疲勞壽命的一種可行的思路，對提高工程結構振動疲勞壽命有一定借鑒意義。

1 振動疲勞理論

1.1 振動理論基礎

自由度系統自由振動，其運動方程為:

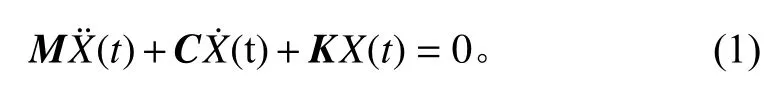
式中：為質量；為阻尼；為剛度，均為×階矩陣。() 為位移向量。一般金屬材料阻尼系數很小，可以忽略不計，式(1)簡化為

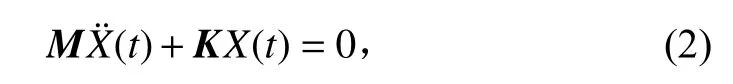
對式(2)傅里葉變換可得：

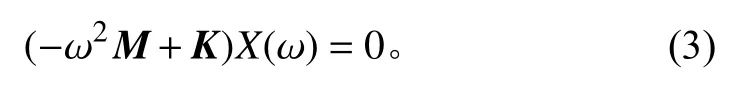
自由度系統受迫振動，其運動方程為：

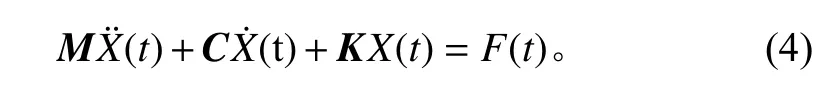
式中：為質量，為阻尼，為剛度，均為×階矩陣。(t)是位移向量，(t)是外部激勵。對式(3)傅里葉變換可得：

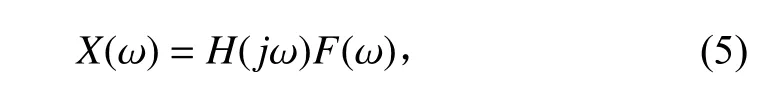
式中(ω)即為頻響函數，其表達式為：

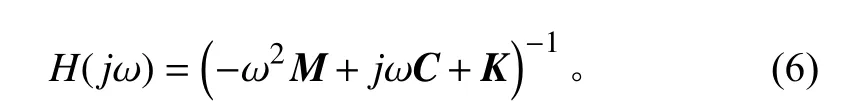
由式(6)發現頻響函數由質量矩陣、剛度矩陣、結構固有頻率和阻尼矩陣確定，而結構固有頻率是受質量分布和剛度分布影響的非獨立變量，因此頻響函數可認為僅受阻尼和結構固有頻率影響。

1.2 隨機振動疲勞計算方法

頻域譜密度方法計算的核心是獲得應力響應功率譜密度，對該功率譜密度分布曲線通過概率統計方法獲得應力峰值期望和正向0 穿期望，再結合-曲線和Miner 線性損傷累計理論估算結構振動疲勞壽命。應力響應功率譜和輸入譜滿足：

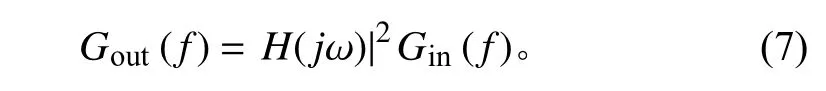
式中：(ω) 為應力傳遞函數；() 為輸入功率譜密度；()為應力響應功率譜密度。以此，振動疲勞計算關鍵在于獲得危險點應力響應功率譜密度函數。

Dirlik 將寬帶隨機過程的幅值概率密度函數定義為1 個指數分布和2 個瑞利分布，由此近似給出的雨流幅值概率密度表達式為：

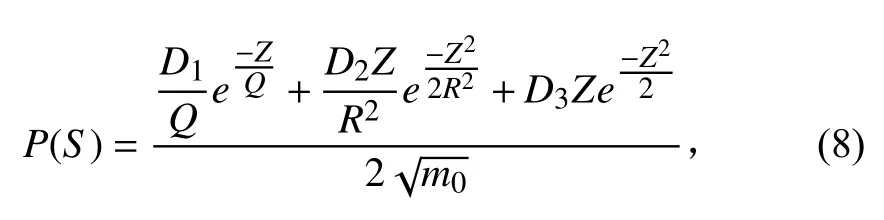
式中各變量表達式為：

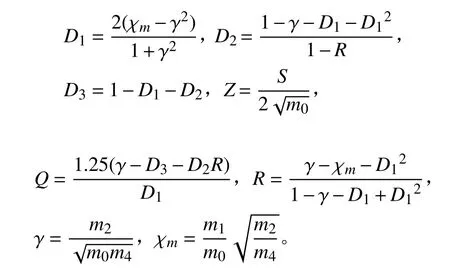
其中：，，，分別為應力響應功率譜密度0 階、1 階、2 階、4 階譜矩；γ為不規則因子，反映帶寬信息。Dirlik 方法對振動疲勞問題具有普適性。

階譜矩計算方法為：

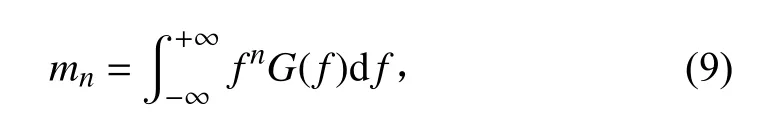
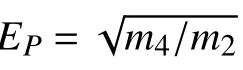
式中：n ，N分別為應力水平為實際循環次數和最大循環次數。以損傷判據=1 來判斷結構失效，聯立公式得壽命計算公式：

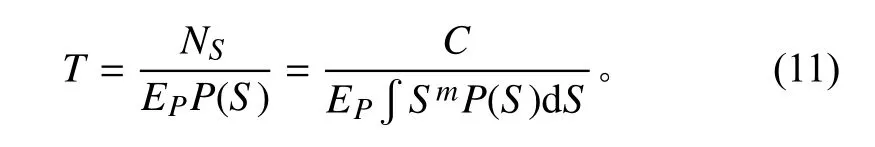
式中：和為S-N 曲線材料參數，為常數。

2 振動疲勞壽命計算

導管后支撐具有對稱性，提取1/5 后支撐作為有限元分析模型。軸套內側節點剛性耦合到軸套中心，約束，方向平動和轉動4 個自由度，外接頭底座與導管內蒙皮鉚釘連接位置設置固支邊界，由于鉚釘位置未出現裂紋，因此未建實體鉚釘模型，有限元模型如圖1 所示。5 083 鋁合金力學性能為：楊氏模量70.3 GPa、泊松比0.33、屈服強度214 MPa、抗拉強度303 MPa、密度2 660 kg/m。需要說明的是子模型局部坐標，，方向分別對應空氣導管內蒙皮圓周切向、內蒙皮圓周軸線方向和內蒙皮圓周徑向。

圖1 有限元模型Fig.1 Finite element model

圖2（a）～圖2（c）為前3 階固有頻率對應的模態振型，圖2(d)為外接頭1 階模態應力分布。模態應力的大小雖然沒有實際意義，但是模態應力反映在該頻率共振時應力集中位置，也是振動疲勞裂紋萌生重要參考，實際裂紋出現在外接頭倒角和計算結果吻合。固有頻率計算結果如表1 所示，誤差滿足精度需求。

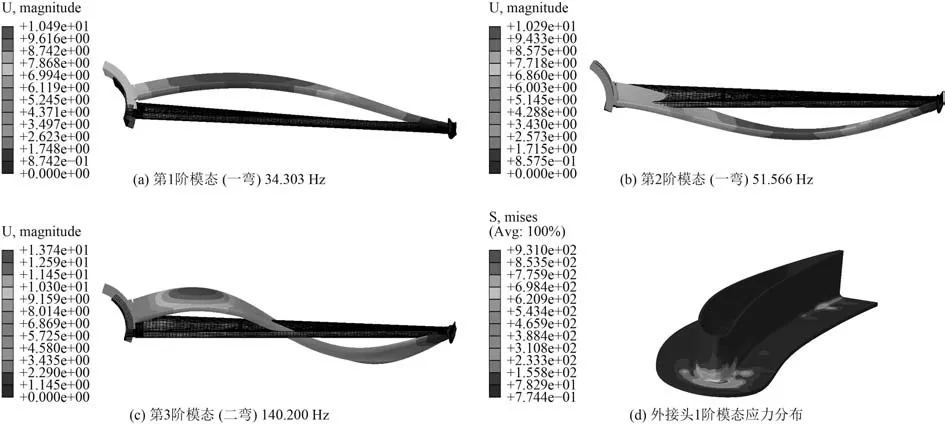
圖2 模態分析Fig.2 Modal analysis

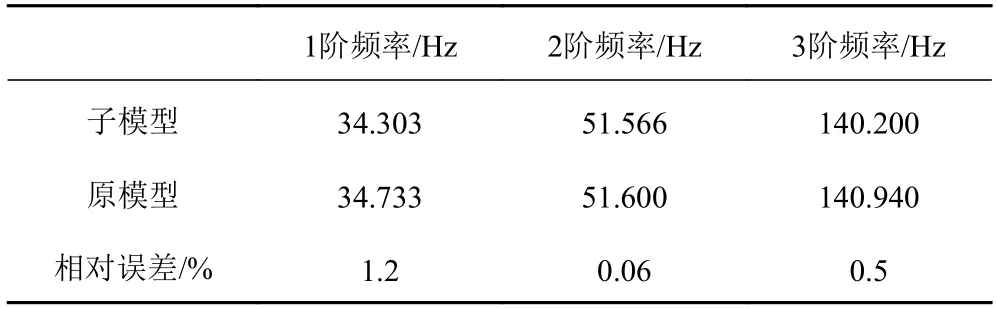
表1 模態分析結果Tab.1 Modal analysis results

利用模態疊加法，在外接頭邊界處施加方向單位加速度激勵，即可求得激勵與結構應力間的傳遞函數，將關注區域節點傳遞函數與波高功率譜密度相乘，便可獲得該節點處應力響應功率譜密度，如圖3(a)所示。采用Dirlik 雨流幅值概率模型計算該模型振動疲勞壽命，最終計算振動疲勞壽命為809.1 h，壽命分布云圖如圖3(b)所示。振動疲勞危險點出現在外接頭前緣倒角處，與1 階模態應力集中位置一致。加速度功率譜是根據該船舶適航某工況實測數據，經過處理后，截取的20～60 Hz 值為2 (m/s)/Hz 的平直譜，每1 h 作用60 s。

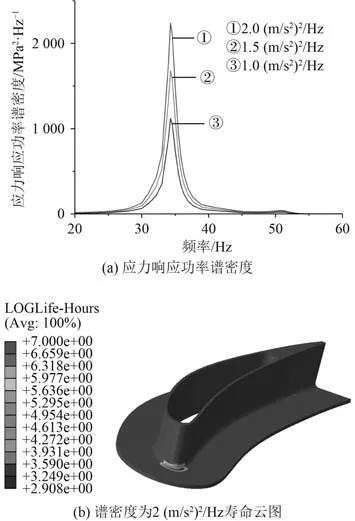
圖3 應力功率譜密度和壽命云圖Fig.3 Stress power spectral density and life prediction

3 振動疲勞影響因素

結構振動疲勞分析主要包括4 部分內容：危險點應力響應、振動疲勞算法、材料疲勞性能和損傷累計理論。主要考慮危險點應力響應和材料疲勞性能對振動疲勞壽命的影響。根據式(5)～式(7)，降低振動激勵下危險點應力響應可以從2 個角度出發：1）通過隔振方法降低外接頭處的振動激勵峰值；2）改變結構固有參數，降低應力響應。

3.1 降低振動激勵

采取適當隔振措施，使加速度功率譜密度降低為1.5 (m/s)/Hz 和1 (m/s)/Hz 時，應力均方根σ分別為72.69 MPa 和59.35 MPa，振動疲勞壽命分別為5 308.8 h和100 000 h，危險點仍在外接頭前緣倒角位置。計算結果表明，降低振動激勵確實可以有效提高振動疲勞壽命；當振動激勵水平較低時，對結構產生的疲勞損傷有限，只有當振動激勵超過某個閾值時，才會引起較為嚴重的振動疲勞問題。

3.2 降低應力響應

根據式(6)，頻響函數是關于結構剛度、固有頻率、質量和阻尼的函數，而結構的固有頻率又是由質量分布矩陣和剛度矩陣共同決定的非獨立變量，因此研究固有頻率和阻尼變化對降低結構振動響應的影響。

3.2.1 調整固有頻率

根據振動理論基礎，結構共振發生在以共振頻率點為中心，半功率點為半徑的頻帶。在載荷無法改變時可以通過調整結構固有頻率避開共振區間。根據式(3)，頻率主要由剛度質量比決定，大幅提升結構剛度使其1 階固有頻率高于60 Hz 很難實現，一般采用附加大質量塊將結構固有頻率降低來避振。集中質量法對低階模態計算精度影響不大，在支臂中段耦合2 個大質量點各12 kg，1 階固有頻率降至16 Hz，振動疲勞壽命如圖4 所示，壽命僅有38 h，危險點轉移至外接頭后緣，與2 階模態應力集中位置一致。因此在增加大質量后，雖然避開1 階共振，但是由于負載提高，2 階模態共振疲勞損傷遠大于原結構1 階共振損傷，壽命減小。

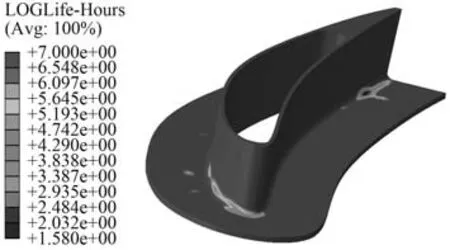
圖4 配重后壽命云圖Fig.4 Life prediction with added mass

3.2.2 模態阻尼比

模態阻尼是影響振動的重要物理量，目前對該參數研究還不夠透徹，工程計算中一般將其視作標量，其數值可以通過實驗測量。描述模態阻尼一般與臨界阻尼系數比較，定義二者比值為模態阻尼比，以此描述該結構阻尼特性。原結構阻尼比為0.03，此處以0.01，0.05 和0.07 的阻尼比研究不同阻尼比下振動疲勞壽命變化趨勢，計算結果如圖5 所示。阻尼比=0.03，應力均方根=83.95 MPa。容易發現危險點應力響應集中于1 階模態處，2 階模態處幾乎為0。

根據圖5，阻尼比0.01～0.03 之間，危險點應力功率譜密度變化劇烈，隨著阻尼比提升，應力響應功率譜峰值急劇減小，結構振動疲勞壽命顯著提升。各阻尼比下危險點應力均方根σ分別為169.48 MPa，64.15 MPa 和53.71 MPa，其振動疲勞壽命計算結果分別為0.027 h，31 622.8 h 和426 579 h。阻尼比變化0.02 會使振動疲勞壽命改變1～2 個數量級，因此阻尼對結構振動疲勞壽命影響極大，對長期處于振動環境的機械結構應在設計階段充分考慮結構的阻尼效應并合理利用。

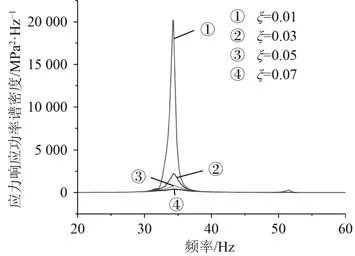
圖5 危險點應力響應功率譜密度Fig.5 Power spectral density of stress response at critical points

3.3 提高疲勞性能

3.3.1 材料影響

結構疲勞性能最直觀的體現在材料的疲勞性能，40CrNiMoA 材料力學性能為：楊氏模量209 GPa、泊松比0.3、屈服強度835 MPa、抗拉強度980 MPa、密度7 830 kg/m。5083 鋁合金和40CrNiMoA 材料的疲勞性能如表2 所示。根據表中數據發現，40CrNiMoA 的楊氏模量和密度約為原結構的3 倍，但由于外接頭處存在邊界約束，質量對固有頻率的影響遠不如剛度，整個結構固有頻率上移。危險點應力響應功率譜密度如圖6(a)所示，由于40CrNiMoA 的楊氏模量遠大于鋁合金材料，危險點處應力響應峰值明顯提升，其應力均方根σ=110.62 MPa，但是并未產生振動疲勞。

表2 材料疲勞性能曲線Tab.2 Fatigue property curve of materials

考慮溫濕的海上工作環境使得不同材料之間的電化學腐蝕嚴重，此處以經過熱處理的5 083 鋁合金材料代替，其S-N 曲線數值見表2，計算結果如圖6(b)所示，壽命為2 642.4 h，相較于原材料的振動疲勞壽命有明顯改善。

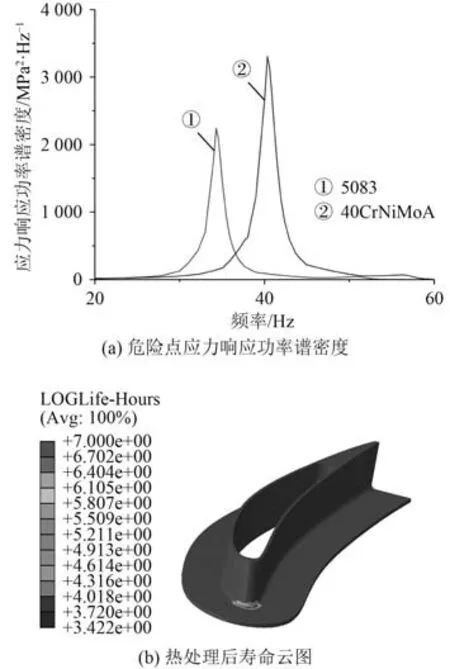
圖6 位移-應力響應及壽命云圖Fig.6 Displacements-stress response and life prediction

3.3.2 局部強化

根據材料力學基礎知識，應力與結構的傳力路線和截面形狀是不可分割的。后支撐承擔部分空氣螺旋槳轉動產生的載荷，是動力系統傳力的重要一環，而外接頭作為后支撐與導管框架連接的唯一零件，其前緣薄壁端極易因剛度不足和應力集中產生疲勞問題。在不改變傳力路線的前提下，試圖通過在外接頭外側增加補強片支撐，變相提高有效截面面積，降低前緣倒角處應力水平。補強片網格與支臂蒙皮和外接頭基座網格部分綁定，模擬鉚接。

局部補強后，原結構的危險點應力響應功率譜密度如圖7(a)所示，由于增加補強片后結構剛度提升，模型固有頻率有所上升，但原模型的危險點應力水平明顯下降，應力均方根σ=39.377 MPa。最終壽命計算結果如圖7(b) 所示，振動疲勞壽命為741 310.2 h，危險位置轉移至后緣倒角處，說明該強化方案有效。因此，工程薄壁結構的振動疲勞可以在薄弱位置適當加強，降低危險點應力水平從而提高振動疲勞壽命。

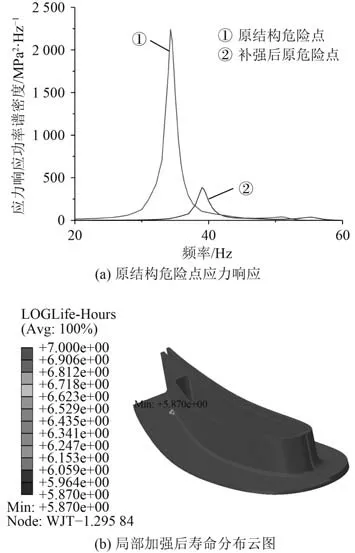
圖7 局部補強計算結果Fig.7 Calculation results of local reinforcement

4 結 語

1) 降低振動激勵，可有效提高振動疲勞壽命，較低水平的振動不會引起振動疲勞；2) 模態阻尼對振動響應影響極大，提高阻尼比可以有效提升振動疲勞壽命；3) 薄壁結構振動疲勞可以從局部加強的角度，改善危險點應力響應水平，延長振動疲勞壽命；4) 疲勞性能優越的材料可以有效提升振動疲勞壽命，但要注意電化學腐蝕等問題，可適當采取熱處理等方式提升材料疲勞性能；5）調整固有頻率避開共振頻帶的方法，對解決共振疲勞問題可能效果明顯，但對于平直功率譜加載，效果可能適得其反。