俄羅斯中學生數學奧林匹克試題中的數學文化

呂孫忠，雷沛瑤，吳尉遲，熊 斌

俄羅斯中學生數學奧林匹克試題中的數學文化

呂孫忠1，2，雷沛瑤1，吳尉遲1，2，熊 斌1，2

（1．華東師范大學 數學科學學院，上海 200241；2．上海市核心數學與實踐重點實驗室，上海 200241）

俄羅斯在數學競賽方面有著諸多經驗值得中國學習，其命制的競賽試題也有著人文特色．研究主要對俄羅斯中學生數學奧林匹克決賽試題中的數學文化進行了研究，統計并分析了其中的數學文化類題目在年份變化、內容分布、知識領域分布和不同年級分布間的特點，從中得到了有關數學競賽命題以及數學資優生培養的相關啟示：以知識源流為切點，架初等高等數學橋梁；思各知識領域特色，精心編排展文化之魅；展現數學內在之美，培養資優生臻美能力；融合文化多元特性，提升資優生國際視野．

俄羅斯；數學競賽；數學文化

1 問題提出

為了選拔一批具有學科特長、創新潛質并有志于服務國家重大戰略需求的青少年，教育部于2018年出臺了《關于實施基礎學科拔尖學生培養計劃2.0的意見》，接著又在2020年發布了《關于在部分高校開展基礎學科招生改革試點工作的意見》（也稱“強基計劃”），并聯合中國科協頒布了《2021年“英才計劃”工作實施方案》，這意味著中國已將拔尖人才的培養提升到了國家重大戰略部署的高度[1]．作為基礎學科的數學，在科技發展和國家競爭中舉足輕重．由于數學學科的特殊性和兒童心智發展的特點，培養數學英才應該把握學生智力發展的關鍵期，中國在對數學英才的早期識別和培育上也做了較多工作[2]．其中，開展數學競賽活動可以在基礎教育階段選拔并培養早期的數學英才，它可以培養學生的興趣、毅力、眼界和品味[3]，并為高等學府選拔科學研究人才．同時，數學競賽也是數學教育研究的一個重要領域，包括對選手和對比賽試題的研究[4]．對試題的研究通常集中在對試題的編制和難度分析、比較等領域[5-6]，對選手的研究主要包括對參賽選手后續發展的追蹤調查[7-9]．這些研究都表明，奧數的學習經歷有利于拔尖人才的成長，對其終身發展是有益的，在英才教育中既應當重視數學奧林匹克活動，也應當關注競賽試題的命制．

數學競賽活動作為一種教育活動，不僅要選拔并培養數學英才，而且要促進學生人性的完善[10]．《普通高中數學課程標準（2017年版）》（以下簡稱《標準》）中指出數學教育的基本理念是：“人人都能獲得良好的數學教育，不同的人在數學上得到不同的發展．”[11]為數學資優生提供更高水平的學習材料，是社會主義教育的題中應有之義[12]．對數學資優生而言，數學試題除了承擔思維訓練的任務，還應具有人文素養的導向，注重數學的價值引領，體現數學的科學價值、應用價值、文化價值和審美價值[11]．數學競賽活動中有不少低年級學生參加，如何讓超常學生在發展數學能力的同時保持對數學的興趣，是開展數學競賽活動應考慮的[13]．眾多研究表明，數學文化可以提高學生的數學學習興趣[14]．因此，在數學競賽試題中融入數學文化，既可以體現數學的人文價值，又可以保持資優生的數學學習興趣，是值得關注的一種命題視角．

國內視域中，無論是已有的數學競賽試題、教材，還是有關數學競賽的研究，對數學競賽試題中的數學文化關注都較少，如何對資優生進行數學文化價值的引領、保持他們對數學學習的興趣還值得進一步思考．國際領域中，數學奧林匹克具有悠久的歷史傳統，它在發現和培養數學人才上發揮著重要作用．其中，不乏菲爾茲獎獲得者的俄羅斯[15-16]在數學競賽試題的人文導向上有著豐富的經驗．俄羅斯對數學人才的培養極富人文精神，數學奧林匹克試圖具有較高的人文情懷，其國家統一考試的數學試題也更注重與實際生活的聯系[17]，數學奧林匹克試題不僅數量多，而且質量高[18]，還有不少奧林匹克式的開放性問題[19]，具有豐富的數學文化背景，為中國數學競賽試題的編制提供了一個值得參考的文化視角．在此背景下，研究提出以下研究問題：俄羅斯中學生數學奧林匹克試題中數學文化類題目在年份變化、內容分布、知識領域分布和不同年級的分布間有何特點？

2 研究設計

2.1 數據來源

全俄中學生數學奧林匹克是受俄羅斯聯邦教育部指導的全國性數學競賽活動，每學年舉辦一屆．從蘇聯解體后到2008年，每屆全俄中學生奧林匹克競賽進行5輪比賽；自2009年開始，原來的校級競賽不再作為首輪的競賽，比賽被縮減為4輪，分別是：市級競賽、省級競賽、聯邦區域賽和全俄決賽，其中市級競賽和省級競賽在第一學期進行，聯邦區域賽和全俄決賽在第二學期進行．全俄決賽通常在每年的4月中旬舉行，時間并不固定，它是俄羅斯最高層次、最高水平的數學競賽，功能和水平與中國的中學數學奧林匹克相當，考試分兩天進行，要求每天在5個小時內完成4道題目．全俄決賽中設置了九年級、十年級和十一年級，與中國高中的3個年級對應，當年的全俄決賽的優勝者有機會代表俄羅斯參加國際數學奧林匹克競賽[20]．

研究的具體對象是1993—2019年俄羅斯數學奧林匹克決賽（以下簡稱全俄決賽）的九年級、十年級和十一年級3個年級的題目，每個年級有8道題目，總計648道題目（由于疫情原因，2020年的比賽沒有舉行），具體的題目來自蘇淳翻譯的兩本書[18，20]．

2.2 分析框架

2.2.1 數學文化類題目的數量變化趨勢

對1993—2019年全俄決賽試題的數學文化進行統計，將每一年3個年級的數學文化類題目總量作為該年的數學文化類題目數量，統計全俄決賽中數學文化類題目數量隨年份的變化趨勢．

2.2.2 數學文化類題目的內容分布

不同學者對數學文化的定義有不同的理解，研究主要采用《標準》中對數學文化的定義，即“數學文化指數學的思想、精神、語言、方法、觀點，以及它們的形成和發展；還包括數學在人類生活、科學技術、社會發展中的貢獻和意義，以及與數學相關的人文活動”[11]．根據汪曉勤依據西方學者所總結的數學史的教育價值以及課程標準中要求的數學的4類價值，研究將數學文化內涵劃分為知識源流、學科聯系、社會角色、審美娛樂和多元文化5個類別[21]，并根據俄羅斯中學生數學競賽題的特點，結合PISA測試對數學問題情境的分類[22]，將“社會角色”細分，得到了數學競賽試題中數學文化元素的分類框架，具體見表1．

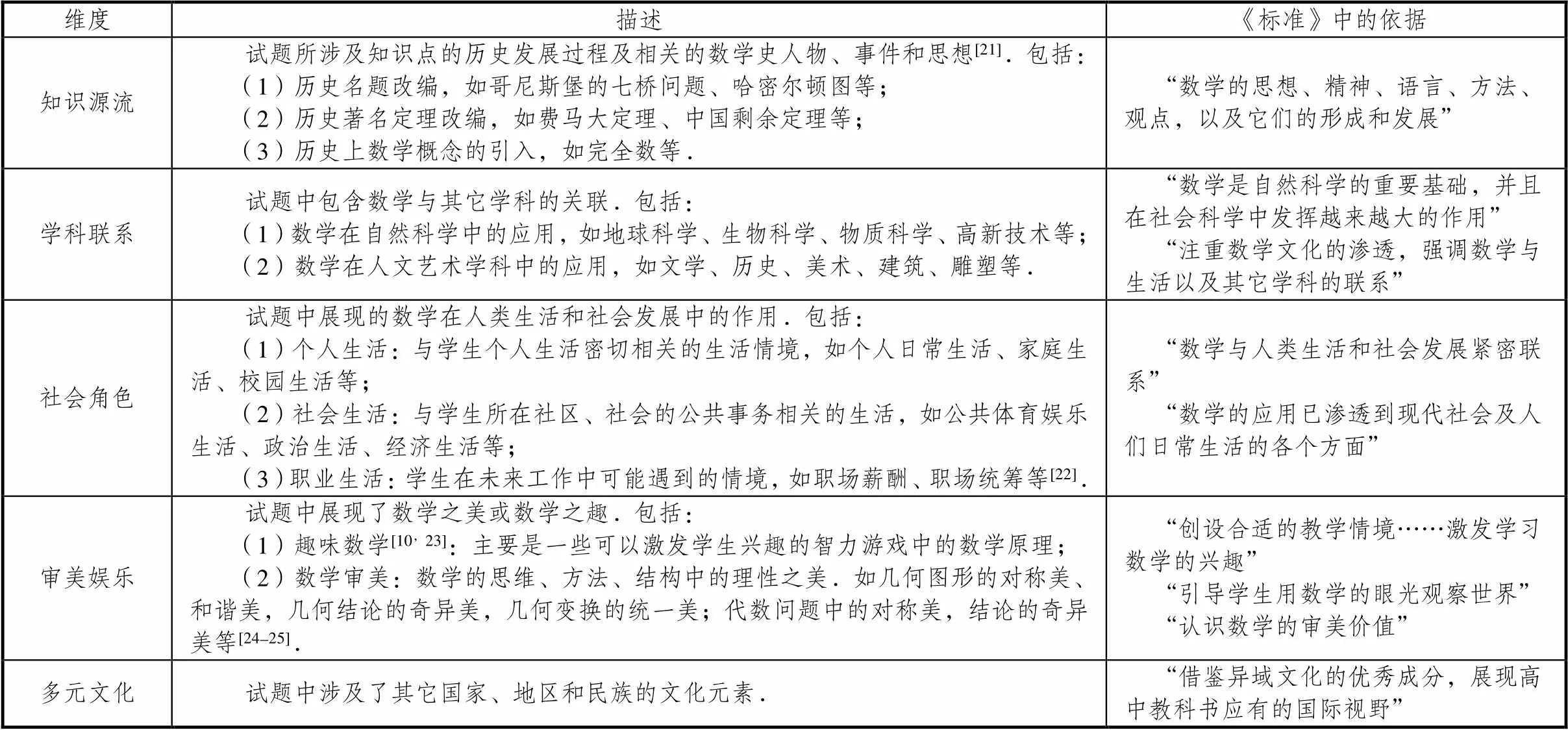
表1 數學競賽試題中數學文化元素的分類框架

具體地，含有數學文化元素的試題舉例如下．

例1 【知識源流】（1999年，十年級）在某個由12個人組成的群體中，任何9個人中都可以找出5個人相互認識．證明：從該群體中可以找到6個人相互認識[18]．

此題和Ramsey原理有一定的關聯，Ramsey理論廣泛見于科研，又頻繁地出現在數學競賽中，Ramsey理論往往以“人與人之間相互認識或者不認識”的關系出現在科普書上[26]．此題多了一個“可以找出5個人相互認識”的條件，是一道典型的根據歷史定理改編的試題，因此將它歸類為知識源流．對這類歷史上著名命題、定理和名題的巧妙改編，可以讓學生感受來自大數學家的思想方法之美，體會數學史上獨特的理性光輝．

例2 【審美娛樂】（2015年，十一年級）不死的跳蚤自原點出發，沿著數軸上的整點跳躍．它第1步躍過的距離為3，然后是5，再然后是9，如此一直下去，在第步躍過的距離是2+1．至于第一步是往左跳還是往右跳，全憑跳蚤自己選擇．試問：跳蚤是否能跳遍每一個整數點（允許多次到達某點）[20]？

此題以跳蚤為主角創造了一個虛擬的故事場景，數軸上的跳蚤不斷跳躍，就像數軸上的點不斷移動，由此產生了相關的趣味數學問題．此類試題將數學問題藏身于有趣的故事情節中，將單調的數學語言用風趣的生活語言代替，新穎有趣，可有效地提升學生的數學學習興趣．

2.2.3 數學文化類題目的知識領域分布

研究根據俄羅斯中學生數學競賽題目所考察的知識點，將題目的知識領域編碼為代數、數論、幾何以及組合共4個知識領域，如表2所示．再分別統計數學文化類題目出現在不同知識領域的數量．編碼中涉及到多個知識點的試題，研究會將該試題歸類到知識點比例較高的領域中去．

表2 知識領域分類框架

2.2.4 數學文化類題目在各個年級上的分布

研究將每一年全俄決賽試題中的數學文化類題目分別統計，由于各個年級的考試同時進行，部分題目會重復出現，針對這一類題目，研究將它們獨立編碼．例如2017年九年級的第8題和2017年十年級的第7題是同一道題，研究會將它們在九年級和十年級中各記一次．

2.3 編碼過程

研究共經歷了3輪編碼，分為預編碼、初編碼和二輪編碼．在確定理論框架后，進入了預編碼階段．研究人員在進行預編碼后，與數學教育專業數學競賽方向的1名教授、3名博士研究生和數學史方向的1名博士研究生討論并確定了具體的編碼方案，隨后開始進行初編碼．在初編碼階段，先由1名研究人員獨立進行編碼，然后隨機抽取20%的題目，也就是6年的原始試題（144道），讓兩名博士研究生分別對數學文化類別和知識領域進行編碼，并統計編碼一致度．得到關于數學文化的編碼一致度為94.44%，關于知識領域的編碼一致度為95.83%．由于編碼一致度較高，研究人員與兩名博士研究生進行討論、達到統一的編碼標準后，展開了二輪編碼．二輪編碼由研究人員獨立將試題進行二次編碼，最終得到研究的數據．

3 研究結果

3.1 數學文化類題目的數量變化趨勢

將1993年到2019年間全俄決賽中3個年級數學文化類題目的總量分別統計，得到折線圖1．

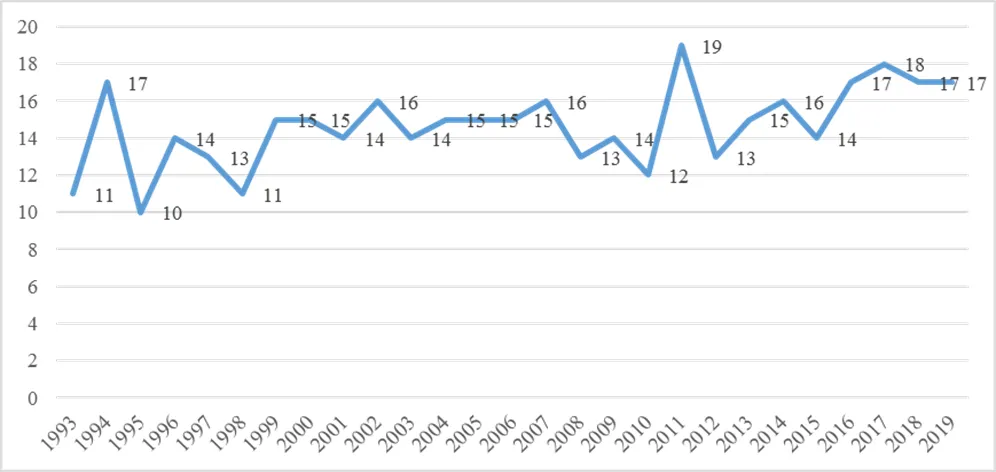
圖1 數學文化類題目數量變化折線圖

容易看出，全俄決賽開展的這27年間，其數學文化類題目所占的權重每年大致相似．在每年3個年級總題目為24題的情況下，其數學文化類題目多在10～20之間波動，大致占比41.7%～83.3%．除了93年（11題）、95年（10題）和98年（11題）外，其余年份的數學文化類題目都超過了50%，這說明俄羅斯一直就十分重視在競賽題中傳遞數學文化．其試題大半具有數學文化背景，有的是有趣的數學游戲情境，有的是自然科學情境，有的是歷史名題改編，有的是題目設計者匠心獨運地通過試題展示數學美，體現數學的審美價值等．

3.2 數學文化類題目的內容分布

將全俄決賽試題的數學文化類試題按數學文化的類別（知識源流、學科聯系、社會角色、審美娛樂和多元文化）分別統計，得到表3和圖2．

從表3和圖2知，全俄決賽試題中的數學文化試題對各個類別的數學文化均有涉及．具體看來，數學文化類試題大量集中在審美娛樂這一類別，占比71.2%，相比其它4個類別具有絕對的數量優勢．其中，數學審美類題目有161道，趣味數學類題目有121道．數學審美類題目主要是通過題目展現一些優美的幾何圖形和代數結構，讓學生感受數學的簡潔美、對稱美、奇異美等，感受數學在永恒與運動間的不同魅力；趣味數學則是將數學試題進行改編，賦予單調的數學題一些有趣的故事情節，或是將數學問題蘊涵在數學游戲中，如方格染色方案的設計、策略游戲中取勝方案的咨詢，或是無限大棋盤上棋子的落定、數學王國中盧布的使用等，讓學生在解題的過程中感受數學文化的樂趣．占比第二多的社會角色類問題，則是將數學競賽與現實生活進行聯系，將數學試題放置于現實生活中個人的、職業的、社會的情境中，讓學生感受數學學科所發揮的社會角色價值，如與個人家庭生活有關的家族相冊、與個人校園生活有關的同學交流、與社會生活相關的體育競技活動以及與學生未來職業生活相關的程序員寫程序等問題，這些問題大多貼近生活，讓學生可以直觀地體會數學在生活中的作用．

表3 數學文化的內容分布統計

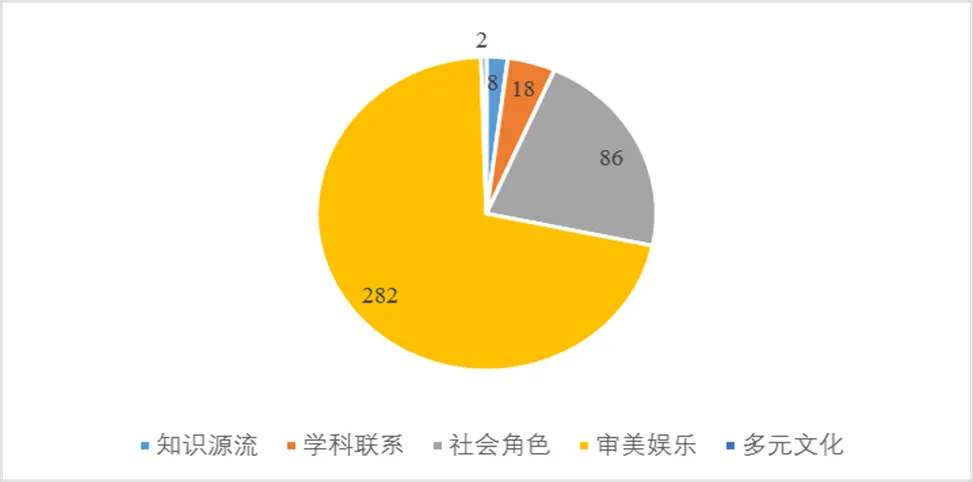
圖2 數學文化類題目內容分布餅狀圖

學科聯系有少量的題目（18道），主要集中在與物理學、航空航天學等學科的聯系，如通過數學方法計算速度、質量，通過數學方法設計航空路線等，這些題目搭建了溝通數學與其它學科的橋梁，讓學生體會數學廣泛的應用性．內容分布最少的是知識源流和多元文化兩個維度．知識源流只有8道題，主要是將數學史上的歷史名題、著名定理等進行改編，如將費馬大定理改編為結構類似，但可以用初等簡單方法解決的不定方程，用哈密爾頓圖改編的圖論路線問題，將歷史上“完全數”概念引入的數論題等，這些改編的資料都可以作為初等數學聯結高等數學的橋梁，它們可以呼喚起學生內心對數學的熱愛，讓他們成為逐夢的數學人．而多元文化僅有2道題，均來自古希臘的神話傳說，出題者別具一格地將古希臘的神話傳說編成數學問題，讓學生在解題的過程中了解多元文化，既增加了數學題目的趣味，又豐富了學生對世界多元性的了解．

3.3 數學文化類題目的知識領域分布

分別統計數學文化類題目在組合、幾何、數論和代數共4個知識領域出現的頻數，得到各知識領域出現數學文化類題目的數量．其中，組合共有42題，幾何共有131題，數論有42道題，代數有181道題．考慮到試題中各個知識領域題目的數量本就不相同，因此將每個知識領域的數學文化類題目的數量除以該領域題目的總量，得到數學文化類題目在4個知識領域的百分比，見圖3．

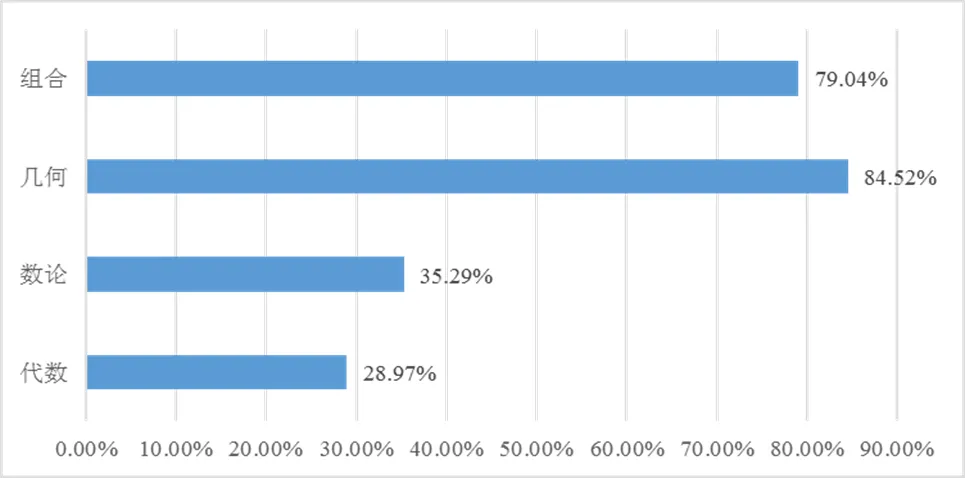
圖3 數學文化類題目知識領域分布條形圖

由圖3可知，數學文化類題目出現最頻繁的是幾何領域和組合領域，占比均在8成左右．其中，幾何試題大部分屬于平面幾何，也有少量屬于立體幾何，這個領域數學文化類題目的占比最高，其高達84.52%的試題具有數學文化背景，但是文化背景的類型較為單一，全部來自數學審美．這些數學美有的是圖形上的對稱、簡潔美、奇異美，如對稱的直線、簡潔的蝴蝶定理、角度的巧合性相等、點的巧合性共圓等；有的是幾何變換中的統一美，如位置在改變的某條直線通過某個定點、變換的三角形保持面積不變、旋轉位似變化下保持的不變性等．歷史上很多優美的平面幾何結論就是在很多人不停地探索中發現的，這些數學美可以激發學生對幾何結論的自主探索，提升學生對幾何位置關系的洞察能力和幾何圖形的審美能力．數學文化類題目占比第二高的是組合領域，其題目中的數學文化背景比重也達到了79.04%．取材廣泛，立意新穎的俄羅斯組合題，需要認真探索、深入思考才能找到試題的答案，是典型性的“動腦題”[18]．組合類題目的文化背景較幾何領域的題目更豐富，有的是設計染色的方案、天平稱重的方案和分割方格紙圖形，有的是游戲策略的輸贏，這些問題大多都十分有趣，貼近生活．同時，組合試題結合了其本身就蘊含的豐富的數學方法，如算兩次、極端原理、反證法、抽屜原理等，將巧妙的數學思想與豐富多彩的數學文化碰撞，產生了無與倫比的火花，這些試題設計精巧卻未令人感到絲毫刻意雕琢之感．另外，有的題目可能還是科研中的副產品，通過解決這些試題，學生也許能在不知不覺中涉足到數學的前沿領域．

數論和代數領域中數學文化類題目占比雖然相對較少，但仍然有3成左右．它們中的數學文化卻更多元，都包含了知識源流、學科聯系、數學審美和社會角色這4個類別，而代數部分還包括了多元文化．從具體內容的角度來說，它們在學科聯系和社會角色上的數學文化類似于組合部分的，但在知識源流和數學審美上有所不同．從數學審美的角度看，俄羅斯競賽中的數論和代數試題也滲透著代數美學，如在數論試題中定義的“好數”“幾乎平方數”“階好數”等，這些概念映射著特殊的代數結構，在代數試題中，不少全對稱或者輪換對稱的不等式也閃耀著數學的美學光輝，而這些都是在組合和幾何試題中看不到的．

具體地，將4個知識領域在5個數學文化類別中的分布進行統計，得到表4．

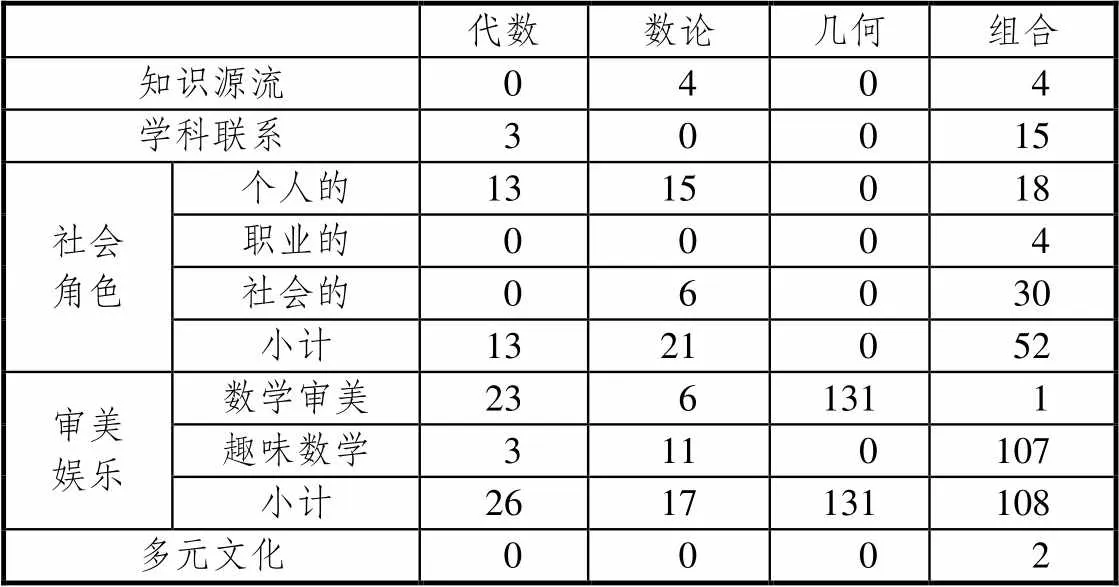
表4 數學文化在各知識領域的內容分布統計

由表4可知，各個知識領域的題目在數學文化各個類別上的分布十分不均衡，利用統計軟件SPSS20.0進行Fisher精確檢驗，得出它們在分布上具有極其顯著的差異（<0.01）．具體看來，組合領域題目所蘊含數學文化的種類最多，涵蓋了5個類別的數學文化，幾何領域所體現的數學文化最單一，僅體現在數學審美上，其余的組合和數論領域也都只涵蓋了4個類別的數學文化．

3.4 數學文化類題目在各個年級上的分布

將試題中九年級、十年級和十一年級的題目分別統計，得到：九年級共148道，十年級共130道，十一年級共118道數學文化類題目．對不同年級題目在5個數學文化類別上的具體分布進行了統計，得到了圖4．

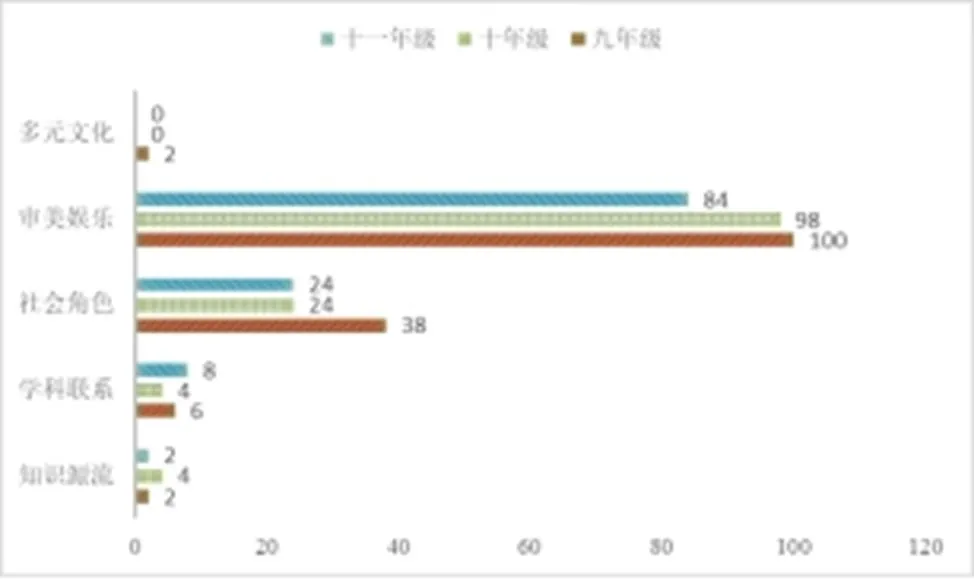
圖4 各個年級數學文化類題目分布條形圖

3個年級數學文化類題目的總數逐漸減少，九年級最多，十一年級最少．這可能與設計者認為高年級學生的抽象能力更強有關．從圖4中可知，盡管總數不盡相同，但各個年級的數學文化類題目在5個數學文化類別上的分布卻大致相似，亦無統計學意義上的顯著差異（Fisher精確檢驗=0.450）．3個年級試題中的數學文化最多出現在審美娛樂這一領域，包括一些體現數學審美的題目和蘊含趣味數學游戲的情境．其次是體現社會角色，重點展現數學與個人生活和社會生活的聯系．而學科聯系、知識源流和多元文化都特別少，尤其是多元文化，試題的里的多元文化僅在九年級出現了兩次．

4 結論與啟示

研究對全俄決賽試題中的數學文化進行了統計分析，針對研究問題，得到了以下研究結論．

（1）全俄決賽試題中數學文化類題目的占比較大，其從1993—2019年的27年間，數學文化類題目所占的權重大致相似且數量大多超過了總題數的一半；（2）在內容分布上，數學文化類題目分布十分不均衡，主要集中在審美娛樂上，多元文化涉及最少；（3）各個知識領域中數學文化類題目的權重也十分不均衡，幾何與組合具有最多的數學文化類題目，且各個知識領域在5個數學文化類別上的分布具有極其顯著的差異；（4）3個年級的數學文化類題目數量隨著年級的增長依次減少，但在5個數學文化類別上的分布具有相同的趨勢．

基于以上研究結論，結合俄羅斯數學競賽的特點，得到有關數學競賽命題以及數學資優生培養的以下啟示．

4.1 以知識源流為切點 架初等高等數學橋梁

全俄決賽試題中有一些試題直接改編于高等數學知識，如數論里的費馬大定理、圖論中的拉姆塞數[26]等，這些試題都具有較深的知識源流，蘊含內隱的數學文化．這些競賽題也可以看作是溝通初等數學和高等數學的橋梁[27]．這也是俄羅斯數學競賽題的鮮明特色，就連俄羅斯著名數學家柯爾莫哥洛夫也曾在1960年打趣道：“也許，找到證明費馬大定理的一種方法是將它作為一道莫斯科數學奧林匹克試題．”[28]數學家們可以將數學研究中部分巧妙的想法，轉化為初等數學語言，然后用美麗的故事將它們包裝成一道道嶄新的數學奧林匹克試題[27]．所以數學奧林匹克試題也值得專業的數學研究人員去探索，因為這些試題可能產生新的研究問題和方向，同時專業的數學研究人員也可以對那部分可以用來作為數學奧林匹克試題資源的高等數學內容保持關注[28]．俄羅斯的數學競賽還得到了許多數學家們的支持，讓學生有更多的機會去接觸更前沿的數學[19]；而歐美國家的許多知名高中也開展了大學數學預科課程，這些預修課程和數學奧林匹克教育可以相輔相成．因此，可以邀請更多的數學家來參加數學競賽的命題、競賽教輔書的編寫和中學數學競賽課程的教學，從知識源流的角度來編制材料，賦予試題更多的數學文化，引導數學資優生更好地從初等數學學習過渡到高等數學的學習和研究中去．

4.2 思各知識領域特色 精心編排展文化之魅

從數學文化內容在各個知識領域分布的角度來看，全俄決賽試題中代數、數論、幾何和組合所蘊含的數學文化類別存在明顯的差異．這些特點也為數學文化融入數學競賽的命題提供了新的思考，在試題編制中應該考慮各個知識領域的特點，為各知識領域的試題融入適合它們知識特點的數學文化，比如幾何題可以從數學審美的角度考慮，而代數、數論、組合題可以結合其它4個角度．但是單純的數學文化展現并不能為學生提供獨特的數學體驗，合理、有效的融合和呈現方式顯得特別重要．數學文化的融入方式并不是盲目的，可以結合其知識特點在現實、歷史和其它學科中的應用情況等進行編制，如數論中的密碼學、組合中的統籌規劃、幾何中的黃金分割等，這些可以增強學生的數學應用意識，同時讓學生認識到數學在其它學科中的重要性，為部分學生成為日后的交叉學科人才打下基礎．另外，全俄決賽試題存在著年級差異，所以在試題與數學文化的融合過程中需要結合該試題的年級特點以及學生的心智發展特點，低年級的競賽試題中可以融入更多的社會角色和審美娛樂的內容，高年級的試題中可以適當地引入知識源流的內容．因此，要將有特色的數學文化滲透到有特點的數學知識和特定年級中去，這樣數學資優生就可以更好地體驗到知識的學習和文化精神的熏陶，擺脫傳統枯燥單純的知識教育[29]．

4.3 展現數學內在之美 培養資優生臻美能力

數學除了具有普適意義的美學特點外，其內在的內容、結構和方法本身就臻于大美．數學的審美價值不僅是用數學的眼光看世界，欣賞文學、美術、雕塑和音樂作品中的數學結構、數學原理之美，還應該讓學生體會數學本身的美，一種純粹的數學之美．而競賽題，是傳遞這些數學之美的有效途徑，正如法國著名數學家、天文學家昂利·龐加勒在《科學的價值》一書中所提到的：“數學的美感、數和形的和諧感、幾何學的雅致感，這是一切真正的數學家都知道的真實的審美感……正是這種特殊的審美感，起著我曾說過的微妙篩選作用，這充分地說明，缺乏這種審美感的人永遠不會成為真正的創作者．”[30]一道好的數學競賽題可以給學生展現出數學的優雅和美麗，會讓他產生對真正數學的熱情[31]．在全俄決賽試題中，平面幾何中幾何圖形的對稱美、和諧美，代數不等式中的簡潔美、奇異美，這些數學美都被設計者精心地編排在題目里，讓學生在解題的過程中感受之美，增強他們的學習動力，提高數學學習興趣，而這些都是在培優數學資優生時值得借鑒的．

4.4 融合文化多元特性 提升資優生國際視野

全俄決賽試題對多元文化涉及較少，27年、3個年級的試題中僅出現了2次多元文化，且都是同一類型，即古希臘的神話傳說．數學作為人類文明的重要組成部分，具有文化多樣性．世界上各個文明和不同的文化之間雖然有質的不同，但卻是值得互相尊重、理解、學習和借鑒的[32]．數學文化同樣如此，不同國家、地區、民族的人在數學創造、數學應用上都有著各自的貢獻，數學文化也有著其鮮明的地域特色．在保留本民族數學的民族特色之外，還應避免狹隘的“民族主義”，應該讓學生了解本民族以外的、廣闊的數學天地和豐富多彩的數學文化．因此，在競賽試題的命制時，可以有意識地融合多元文化，避免文化相對主義、保守主義，展現文化多元性和文明多樣性．這樣培養出來的數學英才，其視野也更開闊，更能包容世間萬物的差異，更能在國際舞臺上走向卓越．

[1] 閻琨，吳菡．拔尖人才培養的國際趨勢及其對我國的啟示[J]．教育研究，2020，41（6）：78-91．

[2] 王光明，宋金錦，佘文娟，等．建立中學數學英才教育的數學課程系統——2014年中學英才教育數學課程研討會議綜述[J]．課程·教材·教法，2014，34（5）：122-125．

[3] 單墫，葛軍．國際數學競賽解題方法·數學競賽史話[M]．上海：上海教育出版社，2019：333．

[4] PETER J T. Future directions for research in mathematics competitions [M] // SOIFER A. Competitions for young mathematicians. Cham: Springer, 2017: 303-328.

[5] KONTOROVICH I. Problem-posing triggers or where do mathematics competition problems come from? [J]. Educational Studies in Mathematics, 2020, 105 (3): 389-406.

[6] 蔣培杰，張勇，熊斌．中外小學高年級數學競賽試題難度的比較研究——以“華杯賽”與“袋鼠賽”為例[J]．數學教育學報，2020，29（6）：87-91．

[7] CAMPBELL J R, WALBERG H J. Olympiad studies: Competitions provide alternatives to developing talents that serve national interests [J]. Roeper Review, 2010 (1)：8-17.

[8] 張勇，何憶捷，熊斌．國際比較視角下奧數優勝者調查結果分析[J]．比較教育學報，2020（6）：83-93．

[9] 陸一，冷帝豪．中學超前學習經歷對大學拔尖學生學習狀態的影響[J]．北京大學教育評論，2020，18（4）：129-150，188．

[10] 朱華偉．從數學競賽到競賽數學[M]．北京：科學出版社，2009：47．

[11] 中華人民共和國教育部．普通高中數學課程標準（2017年版）[M]．北京：人民教育出版社，2018：2-10．

[12] 張奠宙，馬文杰．簡評“數學核心素養”[J]．教育科學研究，2018（9）：62-66，85．

[13] 徐瑞哲，吳瀟嵐．資優生培養要用好數學開放題——奧數國家隊領隊：過早接觸數學競賽存弊端[N]．解放日報，2021-07-19（7）．

[14] 裴昌根，宋乃慶．我國數學文化研究的文獻計量分析[J]．全球教育展望，2017，46（2）：89-98．

[15] USHAKOV D V. Olympics of the mind as a method to identify giftedness: Soviet and Russian experience [J]. Learning & Individual Differences, 2010, 20 (4): 337-344.

[16] GRIGORENKO E L. Gifted education in Russia: Developing, threshold, or developed [J]. Cogent Education, 2017, 4 (1): 1-12.

[17] 張瑞炳，倪明．中國和俄羅斯高考數學考查內容比較研究[J]．數學教育學報，2016，25（2）：32-35．

[18] 阿加漢諾夫．全俄中學生數學奧林匹克[M]．蘇淳，譯．上海：華東師范大學出版社，2009：1-10，63-113．

[19] MARK S, DMITRI F. Russian traditions in mathematics education and Russian mathematical contests [M] // KARP A, VOGELI, BRUCE R. Russian mathematics education. Singapore: World scientific publishing company, 2010：223-252.

[20] 蘇淳．全俄中學生數學奧林匹克[M]．合肥：中國科學技術大學出版社，2020：i-iii，41-80．

[21] 汪曉勤．基于數學史的數學文化內涵課例分析[J]．上海課程教學研究，2019（2）：37-43．

[22] OECD. PISA for development mathematics framework: Reading, mathematics and science [EB/OL]. (2018-09-25) [2021-02-02]. https://doi.org/10.1787/9789264305274-5-en.

[23] 熊斌，談祥柏．趣味數學[M]．上海：上海辭書出版社，2011：1-6．

[24] 張奠宙，木振武．數學美與課堂教學[J]．數學教育學報，2001，10（4）：1-3．

[25] 徐利治．科學文化人與審美意識[J]．數學教育學報，1997，6（1）：1-7．

[26] 熊斌．數學競賽和數學研究[M]．北京：高等教育出版社，2017：115-128．

[27] SOIFER A. The goal of mathematics education, including competitions, is to let student touch “real” mathematics: We ought to build that bridge [J]. Mathematics Competitions, 2012, 25 (2): 47-67.

[28] SOIFER A. Building a bridge I: From problems of Mathematical Olympiads to open problems of mathematics [J]. Mathematics Competitions, 2008, 21 (2): 11-18.

[29] 徐乃楠，孔凡哲，劉鵬飛．俄羅斯高中數學教科書中的數學史及其啟示[J]．吉林師范大學學報（自然科學版），2013，34（4）：152-156．

[30] 龐加勒．科學的價值[M]．李醒民，譯．北京：光明日報出版社，1988：383-384．

[31] SOIFER A. Goals of mathematics instruction: Seven thoughts and seven illustrations of means [M] // SOIFER A. Competitions for young mathematicians. Cham: Springer, 2017: 3-26.

[32] 徐乃楠，劉鵬飛．數學文化熱：歷史、意義與反思[J]．自然辯證法通訊，2020，42（8）：102-106．

Mathematical Culture in All-Russian Olympiad

LV Sun-zhong1, 2, LEI Pei-yao1, WU Yu-chi1, 2, XIONG Bin1, 2

(1. School of Mathematical Sciences, East China Normal University, Shanghai 200241, China;2. Shanghai Key Laboratory of Pure Mathematics and Mathematical Practice, Shanghai 200241, China)

The experience of Russia in mathematics competition is worthy learning, and its competition tests also have humanistic characteristics. This research mainly studies the mathematics culture in All-Russian Olympiad, and the changes of characteristics of mathematical culture between different years, content distribution, knowledge field distribution and distribution by grades are also analyzed. The following results about how to pose mathematics competition questions and how to cultivate math talents are gained. Firstly, to take the history of mathematics as a bridge to link the elementary mathematics and advanced mathematics. Secondly, in consideration of the characteristics of the knowledge field distribution, the mathematical questions should be carefully arranged to show the charm of culture. Thirdly, to use the beauty of mathematics in questions to improve the aesthetic ability of the gifted students. Last but not the least, to integrate diverse cultures to enhance the international vision of gifted students.

Russia; math competition; mathematical culture

G40–055

A

1004–9894（2022）05–0097–06

呂孫忠，雷沛瑤，吳尉遲，等．俄羅斯中學生數學奧林匹克試題中的數學文化[J]．數學教育學報，2022，31（5）：97-102．

2022–05–21

上海市核心數學與實踐重點實驗室課題——數學實踐（18dz02271000）

呂孫忠（1991—），男，浙江溫州人，博士生，主要從事數學競賽與數學教育研究．

[責任編校：張楠、陳漢君]