陣元失效下基于矩陣重構的MIMO雷達DOA估計

陳金立， 張 程， 陳 宣， 李家強

(1. 南京信息工程大學氣象災害預報預警與評估協同創新中心， 江蘇南京 210044；2. 南京信息工程大學電子與信息工程學院， 江蘇南京 210044；3. 南京信息工程大學物理與光電工程學院， 江蘇南京 210044)

0 引言

多輸入多輸出(Multiple-Input Multiple-Output，MIMO)技術給雷達系統性能帶來了全新的突破。與傳統雷達相比，MIMO雷達在目標分辨與參數估計、低截獲以及雜波抑制等方面有潛在的優勢。波達方向角(Direction of Arrival，DOA)估計是MIMO雷達目標參數估計中的重要組成部分，主要有子空間類和稀疏表征類等DOA估計方法。在實際應用中，由于元器件長時間使用老化和惡劣環境的影響會導致天線陣元物理性損壞。由于失效陣元無法正常發射和接收信號，因此MIMO雷達經匹配濾波處理后所形成虛擬陣列中存在大量失效虛擬陣元，則其輸出數據矩陣中存在大量整行缺失元素，破壞了陣列數據的完整結構，導致現有DOA估計方法精度下降甚至完全失效。

針對均勻線性陣列陣元失效下DOA估計精度下降的問題，文獻[7]將單快拍陣列接收信號變換成一個等效低秩矩陣，利用矩陣填充(Matrix Completion，MC)方法求解核范數最小化問題對缺失數據進行填充，但由于該方法僅利用單快拍接收數據，DOA估計精度較低。文獻[8]將陣列接收數據構造成二重塊Hankel矩陣，并利用不定增廣拉格朗日乘子法(Inexacted Augmented Lagrange Method，IALM)對失效陣元的缺失數據進行恢復。文獻[9]針對冗余陣元失效場景下利用虛擬差分陣列中的冗余陣元對協方差矩陣中缺失數據進行填充，但當非冗余陣元失效時，虛擬差分陣列存在空洞，利用虛擬差分陣列無法有效恢復缺失數據，DOA估計性能有待提升。文獻[10]提出冗余虛擬陣元和非冗余虛擬陣元失效場景下的陣元失效DOA估計方法，當冗余虛擬陣元失效時，利用差聯合陣對失效陣元缺失數據進行填充；非冗余虛擬陣元失效時利用陣列冗余度結合MC算法對缺失數據進行恢復。針對存在陣元失效下MIMO雷達DOA估計問題，文獻[11]提出一種基于差分共陣處理的協方差矩陣重構方法，但該方法要求發射陣元的間距為接收陣元間距的倍(其中為接收陣元數)，因此并不能適用于任意結構的MIMO雷達，具有一定的局限性。文獻[12]提出了一種基于塊Hankel矩陣填充的MIMO雷達失效陣元缺失數據恢復方法，該方法利用MIMO雷達虛擬陣列協方差矩陣構造具有四重Hankel結構的低秩塊Hankel矩陣，并利用MC方法填補塊 Hankel矩陣中的缺失數據，得到完整的虛擬陣列協方差矩陣。然而在實際應用中，目標信號只占據空域少量角度分辨單元，目標相對于整個空間來說是稀疏的。因此，MIMO雷達虛擬陣列的采樣數據矩陣不僅具有低秩性且還具有稀疏特性，聯合利用低秩和稀疏先驗，不僅能挖掘矩陣行間或列間元素的相關性，而且還能充分利用行內或列內元素的相關性，這為恢復陣元失效下MIMO雷達采樣數據矩陣中的整行缺失元素提供了可能。

本文將MIMO雷達的陣元失效分為冗余虛擬陣元失效和非冗余虛擬陣元失效兩種情況。當冗余虛擬陣元失效時，對空間上相同位置的正常工作冗余虛擬陣元數據取均值來填充失效陣元的缺失數據。當非冗余虛擬陣元失效時，針對利用虛擬陣列冗余度進行降維填充后的數據矩陣中仍存在整行缺失的數據問題，建立帶有低秩和稀疏二重先驗約束的矩陣填充模型，利用增廣拉格朗日交替方向乘子法(Augmented Lagrange Method-Alternating Direction Method of Multipliers，ALM-ADMM)進行求解得到完整的降維數據矩陣。最后利用root-MUSIC算法估計目標DOA。仿真實驗證明，本文方法能夠有效提高陣元失效下MIMO雷達DOA估計精度。

1 陣元失效下MIMO雷達信號模型

假設MIMO雷達系統具有個發射陣元和個接收陣元，發射和接收陣列均為陣元間隔為半波長的均勻線陣。各發射陣元和接收陣元的歸一化坐標分別記為{T,=-1}和{R,=-1},=1,2,…,,=1,2,…,。假設遠場存在個非相干目標，它們的DOA分別為,,…,，第

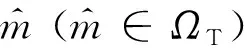
個發射陣元失效和第

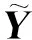
(1)

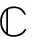
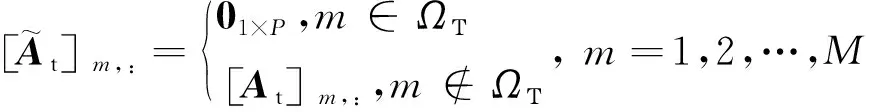
(2)

(3)

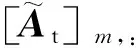
2 不同陣元失效場景下的DOA估計方法

2.1 冗余虛擬陣元失效下DOA估計

MIMO雷達冗余虛擬陣元失效情形如圖1所示，假設接收陣列第2個陣元失效。由圖1可知，空間上同一位置處具有多個冗余虛擬陣元，即使出現失效虛擬陣元仍有正常冗余虛擬陣元能夠輸出數據。因此，可以利用正常工作的冗余虛擬陣元對信號進行降維，將具有個虛擬陣元的虛擬陣列轉換成具有+-1個有效虛擬陣元的等效陣列，實現對失效陣元缺失數據的填補。

圖1 冗余虛擬陣元失效場景

個虛擬陣元輸出信號可以看成一個等效陣列的接收信號，則該等效陣列的陣元坐標可表示為

{=T,+R,|=1,2,…,;=1,2,…,}

(4)

定義集合表示位于空間上相同位置的冗余虛擬陣元編號集合，如下所示:

={(,)|T,+R,=}

(5)

為了降低計算復雜度，本文在降維過程中首先剔除失效虛擬陣元的零元素數據，然后對空間上位置為的正常工作的冗余虛擬陣元數據取均值處理，即

(6)

經過上述處理，不但能夠利用虛擬陣列的冗余度對虛擬陣列輸出信號進行降維，而且能對失效陣元的缺失數據進行填充，等效陣列的輸出數據矩陣為

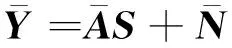
(7)

2.2 非冗余虛擬陣元失效情況下DOA估計

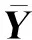
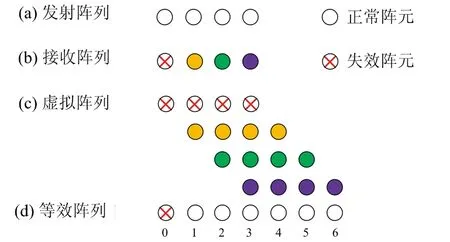
圖2 非冗余虛擬陣元失效場景

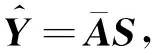
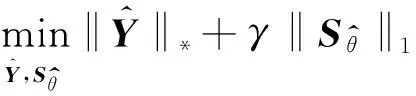
(8)

利用增廣拉格朗日乘子法(ALM)并結合ADMM算法可以有效地求解式(8)中的優化問題。式(8)的增廣拉格朗日函數可以表示為

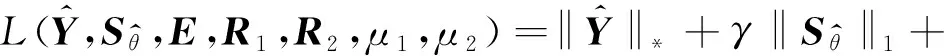
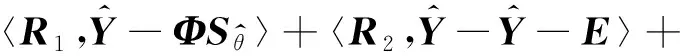
(9)

式中：,為拉格朗日乘子矩陣；，為懲罰因子；〈·〉表示兩個矩陣的內積。

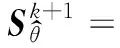
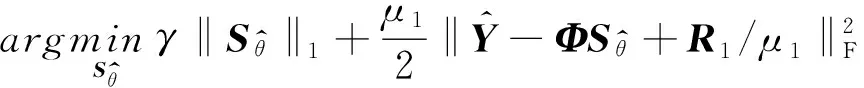
(10)

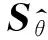
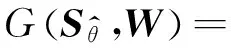
(11)

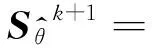
(12)

(13)

式中，(,)=sign()max{||-,0}為軟閾值算子。近端變量的迭代如下：

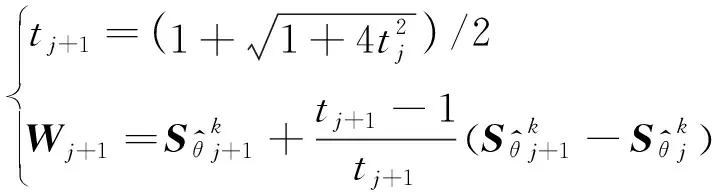
(14)

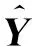
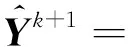
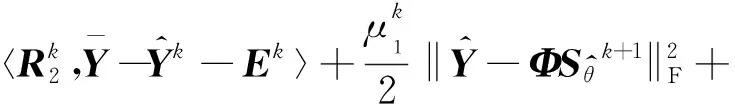
(15)

式(15)可以轉化為求解如下優化方程：

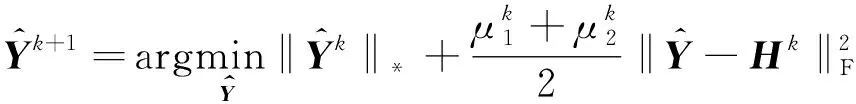
(16)

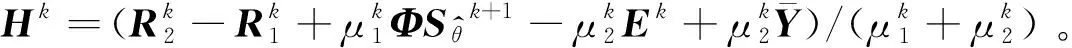
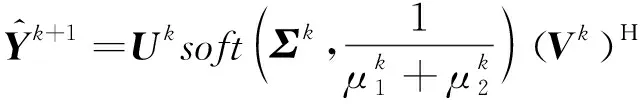
(17)

式中，,分別為的左奇異向量和右奇異向量，為由奇異值組成的對角矩陣，即=()。

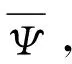
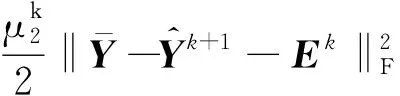
(18)

則的完整迭代解為

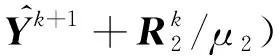
(19)

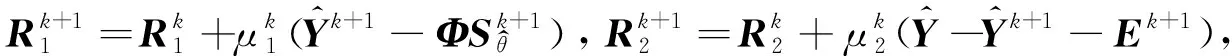
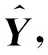
2.3 計算復雜度分析

3 仿真實驗

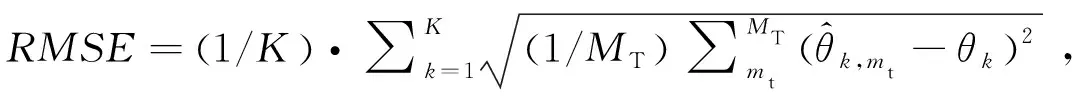
3.1 冗余虛擬陣元失效時DOA估計性能對比

假設發射陣列中第3個陣元失效，接收陣列中第2,5,9,11,14個陣元失效，快拍數為100，信噪比變化范圍為-30～0 dB，進行100次蒙特卡羅實驗，DOA估計均方根誤差隨信噪比變化如圖3(a)所示。由圖3(a)可知，當陣元失效時RD-root-MUSIC算法的目標角度估計誤差明顯大于陣元正常時的估計誤差，表明MIMO雷達的傳統降維預處理方法無法對失效陣元缺失數據進行有效填補。本文方法DOA估計性能要優于文獻[10]方法和文獻[12]方法，低信噪比時與陣元正常時的DOA估計性能接近，而在高信噪比時精度高于陣元正常的DOA估計精度。

假設信噪比為-10 dB，快拍數由50～350變化，其余參數與上述仿真實驗一致，仿真結果如圖3(b)所示。由圖3(b)可知，隨著快拍數的不斷增加，所有方法的DOA估計性能都有所提升，在不同快拍數的情況下本文方法始終能保持最優，且DOA估計精度高于陣元正常時的估計精度。

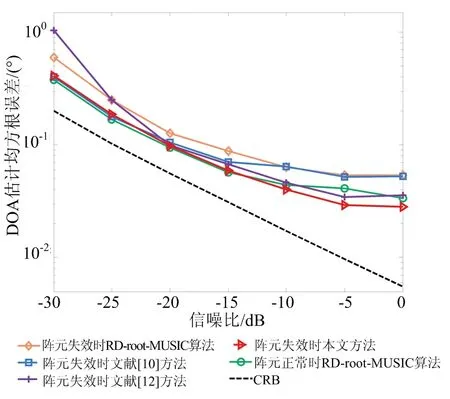
(a) DOA估計均方根誤差隨信噪比變化

3.2 非冗余虛擬陣元失效時DOA估計性能對比

假設MIMO雷達發射陣列第3個陣元失效，接收陣列第3,4,8,11,15個陣元失效，快拍數為100，仿真結果如圖4(a)所示。由圖4(a)可知，隨著信噪比的增加，各種方法的DOA精度也隨之提高，但本文方法估計的DOA更加趨近于陣元正常時的DOA，并且DOA估計性能明顯優于文獻[10]和文獻[12]方法。圖4(b)為目標角度估計均方根誤差與快拍數的變化關系圖，其中信噪比為-10 dB，快拍數由50～350變化，其余參數與上述實驗一致。圖4(b)中可以看出，本文方法的目標角度估計性能在不同快拍數下始終保持最優。

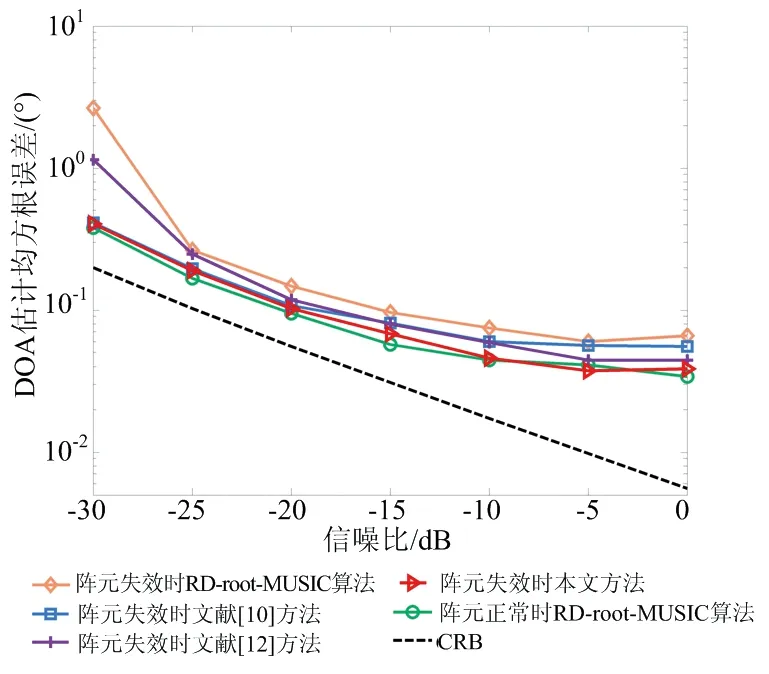
(a) DOA估計均方根誤差隨信噪比變化

4 結束語

當MIMO雷達陣列存在陣元失效時，虛擬陣列采樣數據矩陣出現大批整行目標數據缺失，導致現有DOA估計算法性能下降甚至失效。針對此問題，本文提出了一種基于采樣數據矩陣重構的MIMO雷達DOA估計方法。當冗余虛擬陣元失效時，利用空間上相同位置的虛擬陣元的冗余性對失效陣元缺失數據進行填充；當非冗余虛擬陣元失效時，由于利用陣列冗余度進行填充后采樣數據矩陣中仍有整行元素缺失，因此構造帶有低秩和稀疏先驗約束的矩陣重構問題，利用ALM-ADMM算法進行求解實現對缺失元素的恢復。本文方法能有效避免因陣元失效帶來的DOA估計性能下降的影響，具有較高的目標DOA估計精度。