非Scheimpflug條件對激光三角測距精度影響
陳雪花,肖亞維,黃林海,顧乃庭
(1.中國科學院光電技術研究所, 成都 610209; 2.中國科學院大學, 北京 100049)
0 引言
隨著現代化工業的發展,激光三角測距系統作為高精度、高效率的非接觸測量儀器,在光電技術檢測領域得到了廣泛的應用[1-4]。雖然激光三角法原理在理論上已相當成熟,但在實際應用中還有一定的困難。比如測量自由度、測量范圍、可測量材料類型等性能都有待改善[5-8]。在成像系統結構方面,激光三角測距需要對成像系統進行精確設計,保證激光光斑在成像系統中能時刻聚焦,即成像系統滿足Scheimpflug條件[9-10]。滿足Scheimpflug條件會給激光三角測距的實際應用帶來困難,原因在于:① 成像系統要滿足Scheimpflug條件,即將激光器軸線光束、成像透鏡主平面和光敏面三者的延長線相交于一點,精確的角度控制要求給實際應用帶來不便;② 成像結構不穩定;③ 由于需要開展定制化系統設計,系統成本高。因此,可考慮在實際應用中采用相機與鏡頭同軸化直接集成的方式,構建非Scheimpflug條件下的激光三角測距模型。相較于滿足Scheimpflug條件的非同軸激光三角測距系統,同軸化直接集成的激光三角測距系統相機光敏面與鏡頭主面平行,符合一般成像系統接口方式,無需定制化設計,且鏡頭與相機結構更緊湊,使用簡單方便的同時顯著提升系統穩定性并降低成本[11-15],但這不可避免地降低激光三角測距精度。在激光三角測距精度影響研究方面,部分學者開展了相應分析,如周坤等[16]研究了被測量物體顏色與傾角對測量精度的影響;Miks等[17]利用幾何光學理論,證明了由于透鏡像差的存在即使滿足Scheimpflug條件也不能清晰成像;Zhong等[18]利用失焦理論校正了Scheimpflug系統中的失焦問題。上述文獻對激光測距精度影響因素做了深入分析,推動了激光三角法高精度測距技術發展,但均只針對滿足Scheimpflug條件的激光三角測距方法進行測距精度分析,并未針對非Scheimpflug條件對激光三角測距精度影響進行分析。
1 非Scheimpflug條件激光三角測距解析模型
在激光三角測距系統中,為了使物體在移動過程中,像點與物點始終滿足物像關系,從而在光敏面上成清晰像點,其成像系統的光路設計應滿足Scheimpflug條件[19],滿足Scheimpflug條件的激光三角測距原理如圖1所示。
在圖1中,建立激光器的軸線光束AB、成像透鏡主平面AO和光敏面三者的延長線交于A點的非共軸結構,需要精確控制角度讓三者相交于一點比較困難和復雜。因此,在實際應用中,常采用鏡頭主平面與相機光敏面平行的安裝方式,即采用相機和鏡頭同軸化的激光三角測距系統,這種方式雖然由于不滿足Scheimpflug條件導致測距精度降低,但也提升了系統穩定性,簡化了系統,并降低了成本。
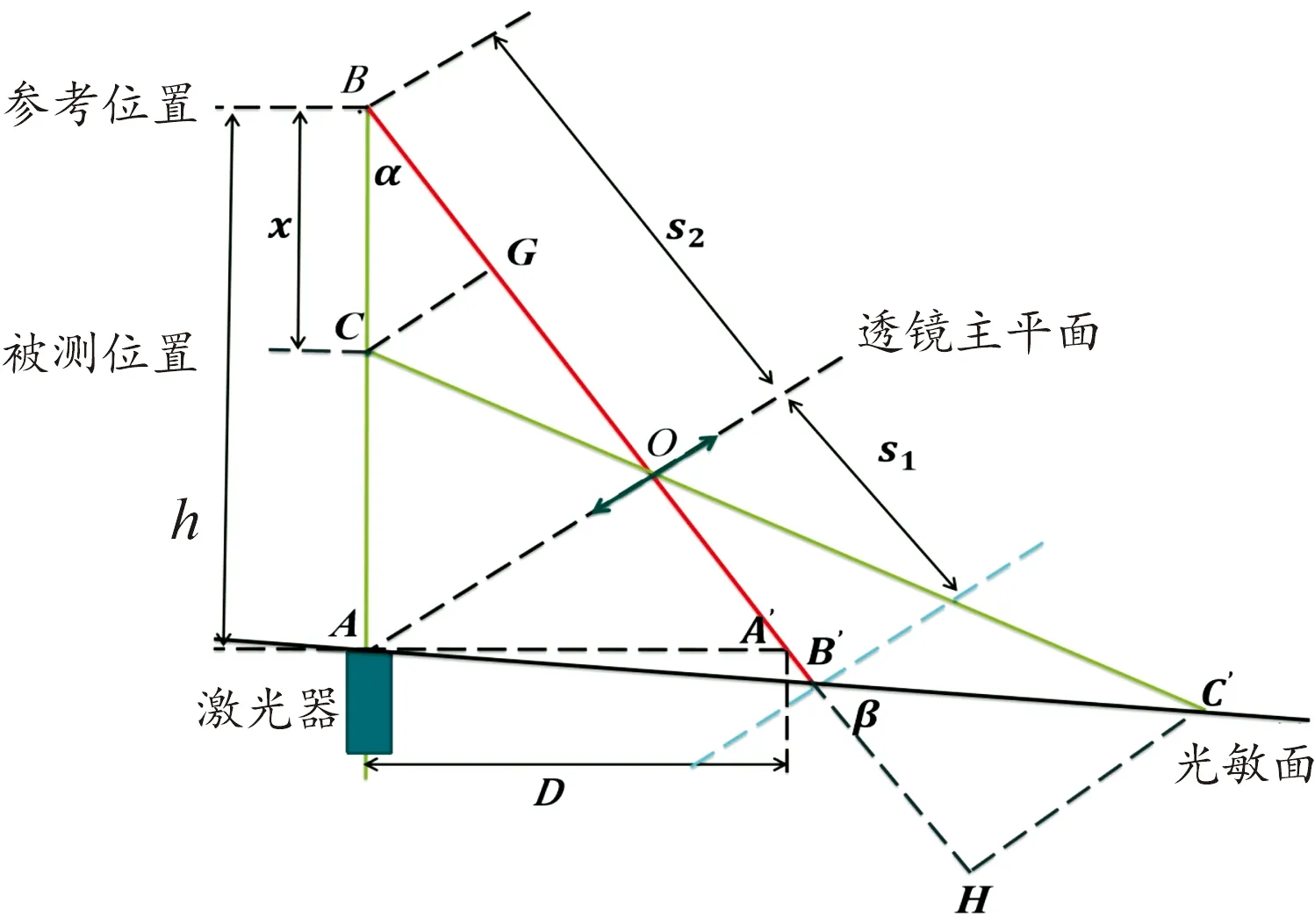
圖1 滿足Scheimpflug條件的激光三角測距原理圖
非Scheimpflug條件激光三角測距原理如圖2所示,B點為參考位置,BB′是鏡頭光軸;AA′垂直于AB,A′點到激光發射器A點的距離為D,定義為基線;h為參考位置B到激光器出射點A的距離,定義為工作距。當被測物體從參考點位置移動x距離時,測量點C通過鏡頭成像于光敏面上M點,工作距不同的點(B點和C點)成像在光敏面上的位置是不同的,所以可利用這一規律實現距離測量。

圖2 非Scheimpflug條件激光三角測距原理圖
在圖2△OCG和△OMB′中,有∠COG=∠MOB′,∠OGC=∠OB′M=90°,由三角形相似可知:
(1)
解算出距離x,其由下式給出:
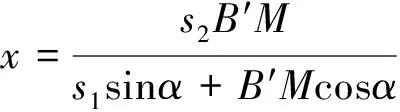
(2)
式中:B′M為光敏面上反射光斑的相應位置變化量;s1為成像鏡頭的成像距離,即成像鏡頭主平面與光敏面中心之間的距離;s2為成像鏡頭的物距,即被測物體參考位置與成像鏡頭主平面之間的距離;α是工作角,即入射光與參考位置處反射光之間的夾角;β是光敏面與成像鏡頭光軸之間的夾角,定義為成像角。當被測點位于參考位置下方時,x取正值,當被測點位于參考位置上方時,x取負值。
參考位置B點無論是否滿足Scheimpflug條件都能理想成像,所以有:
(3)
s1tan(β)=s2tan(α)
(4)
根據圖2可知,
(5)
s2=hcos(α)
(6)
在△OB′C′中使用正弦定理可得,
(7)
(8)

(9)
其中,
∠B′C′M=β-∠COG
(10)
(11)
為了計算更方便,定義激光三角測距系統的系統參數工作距h、基線D、鏡頭焦距f為已知量。聯立基于圖2推導的式(3)—式(11),可得到式(2)中的s1、s2、α、β、B′M未知量,實現距離x的測量;在實際應用中,通常B′M是通過圖像處理獲得的。
在相同系統參數的Scheimpflug條件和非Scheimpflug條件激光三角測距模型中,B′M小于B′C′,所以非Scheimpflug條件激光三角測距系統相比于Scheimpflug條件激光三角測距系統的靈敏度更低,且存在失焦。
2 非Scheimpflug條件激光三角測距誤差
為了分析非Scheimpflug條件相對于Scheimpflug條件引入的失焦距離,建立了如圖3所示的失焦距離計算模型。參考點B點無論成像系統是否滿足Scheimpflug條件都能夠理想成像;對于偏離參考位置C點發出的光束受鏡頭口徑的限制,上光線和下光線分別為CFC′、CEC′,主光線COC′與光敏面和理想成像面不垂直。把激光光源看作是理想點光源,對于滿足Scheimpflug條件的成像系統而言,B點和C點能夠理想成像,但當處于非Scheimpflug條件下時,相機光敏面并不處于物像關系對應平面上,存在失焦距離并引入離焦像差。

圖3 失焦距離計算模型
對△MB′C′使用正弦定理可得失焦距離:
(12)
為了進一步分析非Scheimpflug條件引入的失焦距離對激光三角測距精度的影響,可通過建立錐形光束獲得光敏面上的能量分布分析理論中心位置與質心位置之間的定位誤差,進而解算非Scheimpflug條件下距離測量誤差。
在圖3中,垂直于主光線傳輸面的能量相等,并且每個傳輸面上總能量相等,因此可以通過定義錐形光束得到光敏面上的能量分布。對于光束傾斜入射的旋轉對稱光學系統,只有一個方向上的光場分布會發生改變,所以只需獲取該方向上的能量分布。根據圖3的失焦距離計算模型可定義錐形光束,錐形光束截面圖如圖4所示。
在圖4中,鏡頭光軸垂直于鏡頭主平面EF,光敏面平行于鏡頭主平面;FT垂直于CC′,ES垂于CC′;鏡頭的口徑直徑為d。對于偏離參考點x位移并以與光軸夾角為∠COG角度入射的光束,其主光線CC′經過透鏡中心O分別傾斜入射到光敏面上M點和理想成像面上C′點。要獲得光敏面上的光場分布,直接仿真錐形光束截面FC′E比較困難。可用錐形光束截面F′C′E′代替錐形光束截面FC′E,獲得光敏面上的能量分布。

圖4 錐形光束截面圖
為了進一步簡化仿真過程,將主光線CC′所在的坐標系順時針旋轉∠COG角度與光軸重合,并在XOY坐標中建立數值仿真模型如圖5所示。
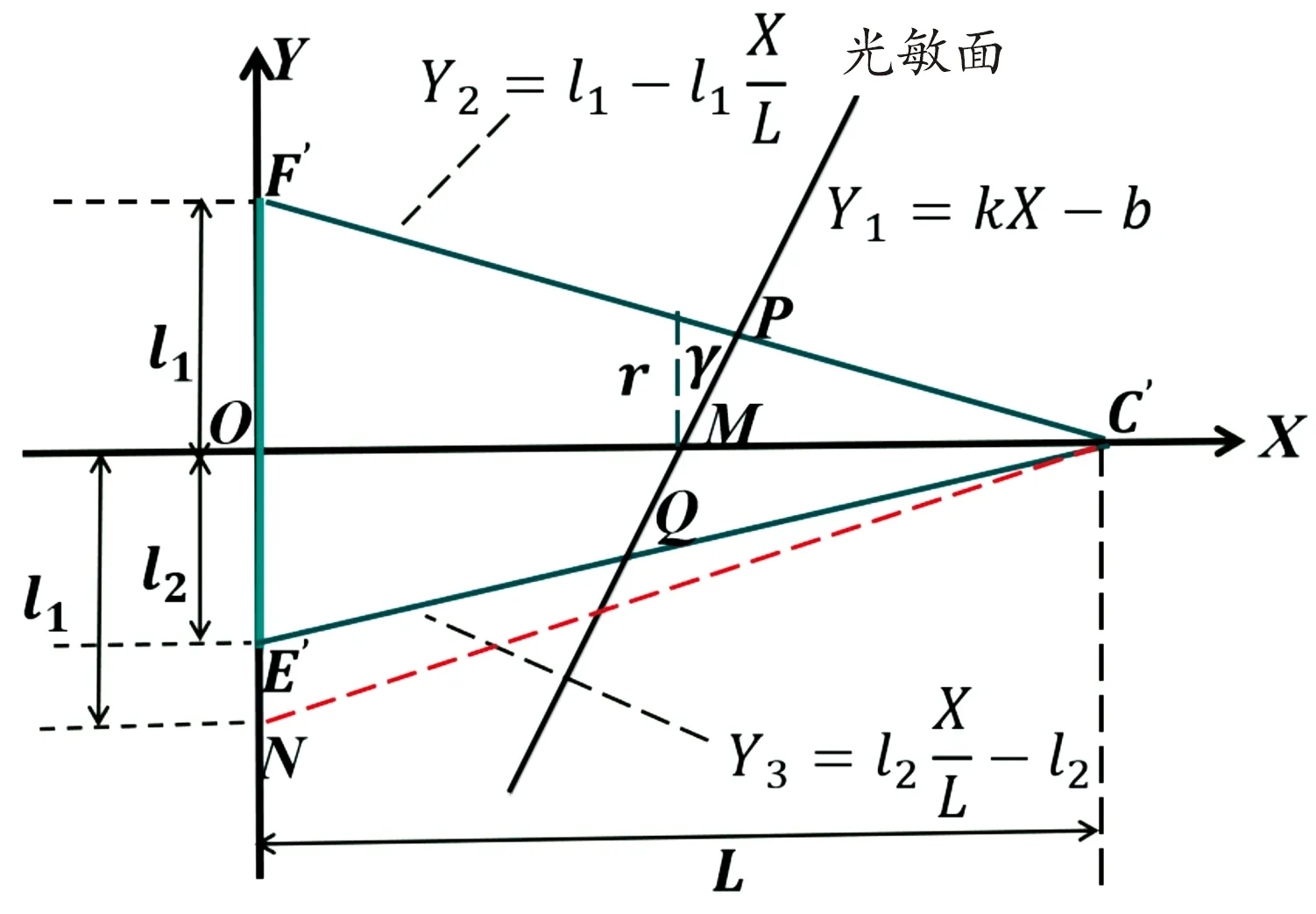
圖5 XOY坐標系中錐形光束模型
由于∠F′C′O和∠E′C′O不相等,Matlab定義錐形光束就比較困難,但可以建立錐形光束截面F′C′N代替錐形光束截面F′C′E′。無論是錐形光束截面F′C′E′還是錐形光束截面F′C′N,垂直于OC′主光線的總能量不變。所以錐形光束截面F′C′N可以代替錐形光束截面F′C′E′。建立錐體截面模型F′C′N需要確定錐高、錐底半徑、錐半角、能量分布。
1) 錐半角。
根據圖4可知,
(13)
(14)
當x取正值時,∠FC′O′大于∠EC′O′,錐角為∠FC′O′;當x取負值時,∠FC′O′小于∠EC′O′,錐角為∠EC′O′。為了簡化分析過程,下面的分析過程都以x取正值為例。
2) 錐底半徑。
錐底半徑的取值是根據上述的錐角所確定的,根據圖5的幾何關系可知,
l1=OC′tan(FC′O)
(15)
3) 錐高。
在圖3中,△OBC使用正弦定理可知:
(16)
由于點C和點C′滿足理想成像,所以CO和C′O滿足:
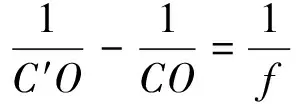
(17)
聯立式(18)和式(19)可知錐高為:

(18)
4) 錐形光束能量分布。
在圖5中,光束傳輸到位置X時,對應傳輸面上強度均值表達式為:
(19)
r=(L-X)tan(∠FC′O)
(20)
式中,Ia為總光能量。
Y1為光敏面上能量分布變化方向上的強度分布,可以用以下方程描述:
Y1=kX-b,(X∈(Q,P))
(21)
式中,k=tan(π/2-γ),b=k(L-C′M),γ=∠COG。
對于Y1定義域X取值范圍的計算:在XOY坐標系中,
(22)
(23)
聯立方程(23)—(25),可求出Q,P的坐標分別為:
(24)
(25)

通過對錐形截面光束錐高、錐底半徑、錐半角及能量分布的定義,可以獲得任意非Scheimpflug條件激光三角測距模型光敏面上的能量分布,為分析非Scheimpflug條件下光斑定位誤差及激光三角測距誤差提供了前提條件。
質心法[20-21]廣泛應用于激光三角測距的光斑定位,因此本文采用質心法研究非Scheimpflug條件對激光三角測距精度影響。在圖5中,設利用質心法計算出的坐標點為(m,n);理想點M點的坐標為(b/k,0),則質心法定位誤差σ:
(26)
將定位誤差σ代入到測距式(2)中,可得測距誤差表達式為:
(27)
3 數值仿真分析
3.1 特定激光三角測距系統參數對比分析
Ye等[22]采用透鏡焦距f=25 mm、透鏡口徑直徑d=20 mm、工作距h=30 mm、基線D=10 mm系統參數搭建了滿足Scheimpflug條件的激光三角測距模型,并實現了在±10 mm范圍內的測量誤差22.4 μm。
將參考文獻[22]中的系統參數代入本文的誤差模型中,數值仿真結果如圖6所示,圖6(a)~(c)分別為失焦距離、光斑定位誤差、測距誤差隨測量距離x變化曲線。測量距離x取正值時,工作距越小;測量距離x取負值時,工作距越大;測量距離x絕對值越大,偏離參考點的距離越大。根據式(2)激光三角測距公式可知,測量距離x與光敏面檢測到的偏移量B′M為非線性關系,并且傾斜的物平面,導致三角測距系統存在非旋轉對稱像差、分辨率不均勻、強度分布不均勻等問題[17]。所以在圖6中偏離參考點相同測量距離的失焦距離、光斑定位誤差、激光三角測距誤差失對稱;并且被測點偏離參考位置越大,失焦距離、光斑定位誤差、非Scheimpflug條件激光三角測距誤差越大。
根據圖6(c)可知,非Scheimpflug條件下的激光三角測距誤差是相當大的,只有測量范圍約(-2 mm,2 mm)時,才能達到參考文獻[22]中的測量精度,因此在該系統參數下,不能實現高精度、大范圍的測量。由于不同系統參數的測距精度是有差異的,因此分析不同激光三角測距模型對非Scheimpflug條件激光三角測距法的應用尤為重要。
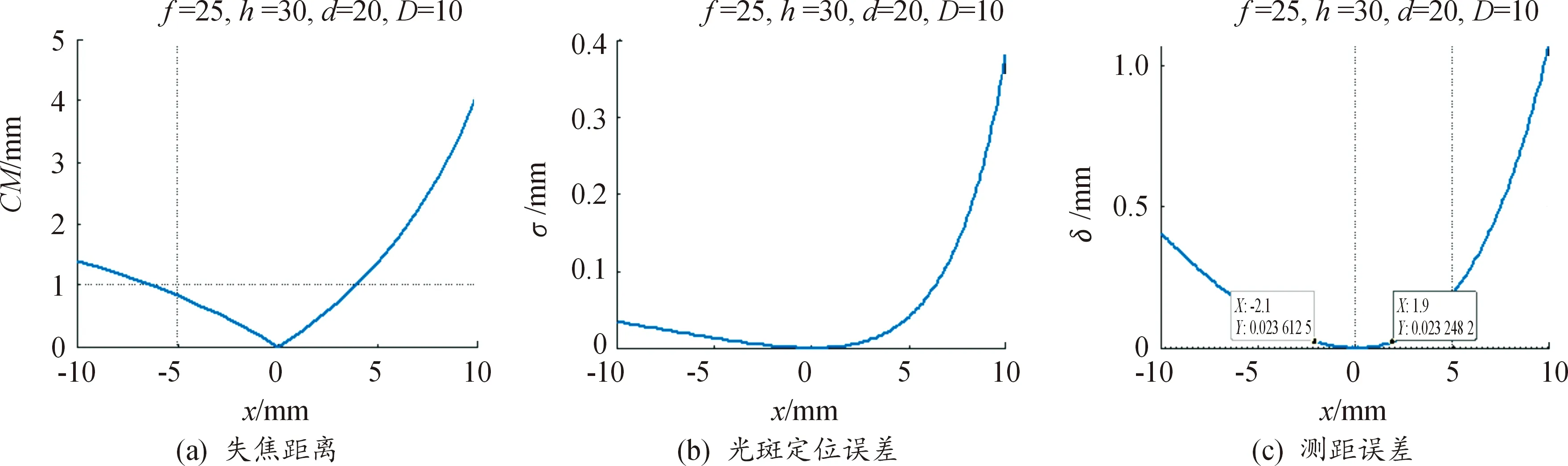
注:其中f為鏡頭焦距、h為工作距、D為基線、d為孔鏡頭徑、x為被測點與參考的距離
3.2 不同激光三角測距參數對比分析
激光三角測距系統作為高精度、高效率的非接觸測距儀器,常用于短距離測量,以保證測量精度。本文分析的系統參數是針對短距離、高精度測量的,并且不同系統參數下的激光三角測量精度及測量范圍是不同,因此在相同測量范圍內分析測量精度隨不同系統參數的變化才有意義。
在非Scheimpflug條件激光三角測距解析模型中,激光三角測距系統的系統參數工作距h、基線D、鏡頭焦距f決定了工作角α、成像角β、物距s2、像距s1、失焦距離C′M,進而影響激光三角測距精度。因此,只需要分析系統參數:工作距h、基線D、鏡頭焦距f就能實現對不同激光三角測距模型測距誤差的分析。
一般鏡頭與相機結構比較緊湊,因此在仿真中采用了比較小的短焦距鏡頭;根據光敏面尺寸大小選擇工作距及基線,以保證測距系統有足夠大的測量范圍。本文以BASLER公司acA4024-29 μm光敏面大小7.4 mm×5.6 mm為基準,所選擇的系統參數在測量范圍±10 mm內光斑都必須在該光敏面上成像。
圖7為不同激光三角測距模型數值仿真結果,數值仿真流程如圖8所示。

注: f為鏡頭焦距、h為工作距、D為基線、d為孔鏡頭徑、x為被測點與參考的距離
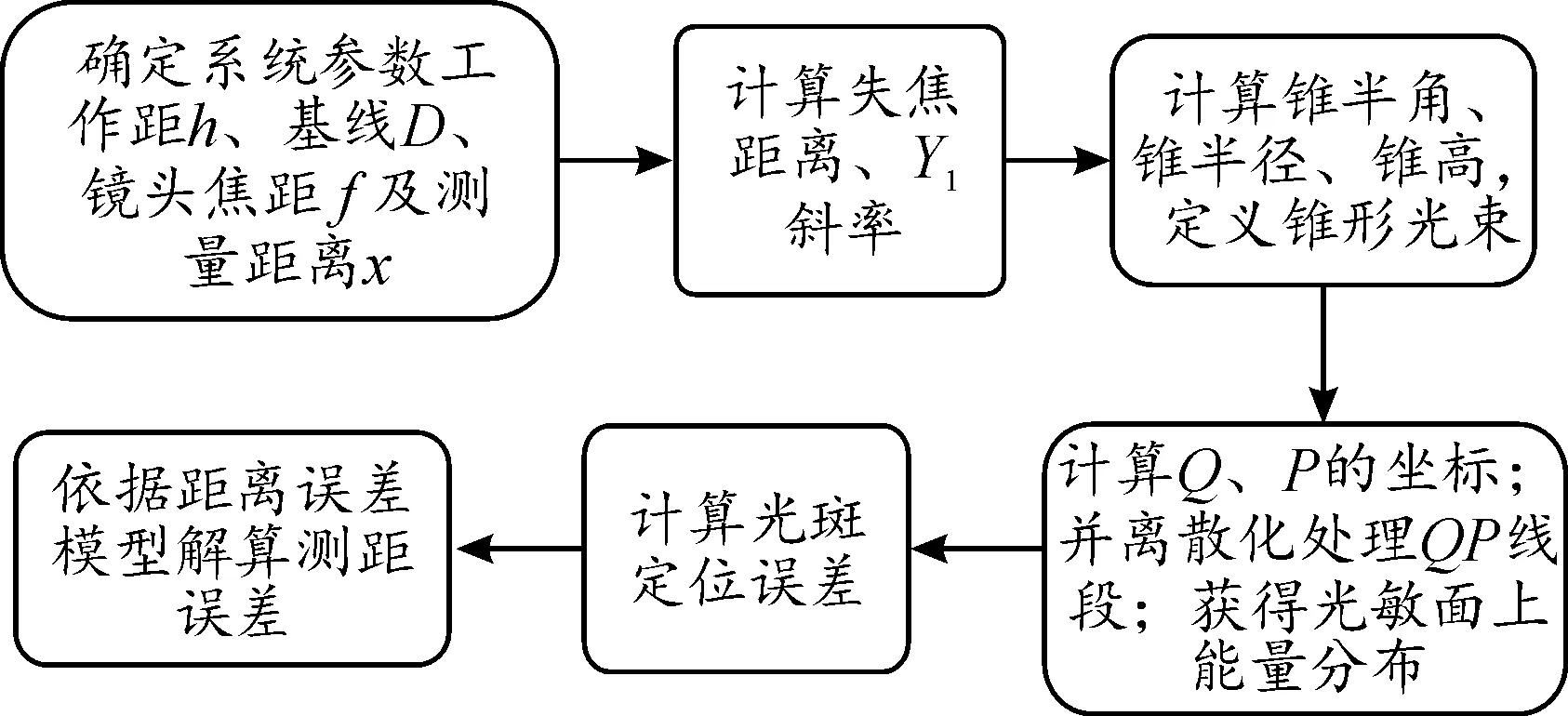
圖8 數值仿真流程圖
在圖7中,f為鏡頭焦距、h為工作距、D為基線、d為孔鏡頭徑、x為被測點與參考的距離。圖7(a)~(c)分別為不同工作距對應的失焦距離、光斑定位誤差、測距誤差,圖7(d)~(f)分別為不同基線對應的失焦距離、光斑定位誤差、測距誤差,圖7(g)~(i)分別為不同焦距對應的失焦距離、光斑定位誤差、測距誤差。現對圖7中曲線變化趨勢原因進行分析。
1) 在圖7 (a)、(b)、(c)中,工作距越大失焦距離、光斑定位誤差、測量誤差都越小,這是由于在較大的工作距下,工作角較小,系統靈敏度較低(放大倍率較大),因此受非Scheimpflug條件的影響較小。
2) 在圖7 (d)、(e)、(f)中,基線越大失焦距離、光斑定位誤差、測量誤差越大,這是由于在較大的基線下,工作角較大,系統靈敏度較大,因此受非Scheimpflug條件的影響較大。
3) 在圖7 (g)、(h)、(i)中,由于焦距越大,光敏面與理想成像面的夾角越大的原因,導致失焦距離越大。但對相同的基線、工作距的系統,主光線(例如圖3中的CC′)與光敏面的夾角(圖3中∠OMB′)不變,導致不同焦距的光斑定位誤差相差不大。但由于焦距越大,成像距離s1越大,系統的放大倍率越小,所以(i)中的激光三角測距誤差越小。
4) 在圖7 (c),(f)、(i)中,工作距越大、基線越小、焦距越大,受非Scheimpflug條件的影響較小。
通過對不同激光三角測距模型測距誤差分析可知,在非Scheimpflug條件下要實現較大范圍高精度的測量應選擇工作距大、基線小、焦距大的系統參數。比如,要達到參考文獻[22]中的測量精度,可以采用工作距h=100 mm,基線D=10 mm,焦距f=50 mm的系統參數,仿真結果如圖9所示。最大的測量誤差為22.4 mm和參考文獻[22]的測量誤差相當。因此在非Scheimpflug條件激光三角測距應用中,可以根據測量精度及測量范圍需求選擇合適的系統參數,也是可以實現較高精度測量的。
在實際應用中,除了考慮不同工作距、基線、焦距系統參數對非Scheimpflug條件激光三角測距精度的影響外。激光三角測距采用的高斯光束激光光源的光斑尺寸會隨著測量范圍變大而變大,這降低了被測物面位移較大時的分辨率。改進的方案不僅可采用準直透鏡,使光斑均勻分布,而且可直接采用無衍射光束代替高斯光束。與此同時,在實際應用中鏡頭成像不是完全理想的,因此并不能保證空間所有點通過同一個光學中心。當物體離鏡頭光軸較遠或者鏡頭相對于像距和物距很大時,鏡頭會出現比較嚴重的初級像差,因此在激光三角法測量系統中,需要對鏡頭的像差進行補償[23]。

圖9 激光三角測距誤差
針對系統隨機噪聲降低質心位置提取精度的問題。一方面在采集圖像前,合理修改圖像傳感器的參數,在相機前面加入窄帶濾波片等方式,可以有效地減少探測器的基底偏置及背景中的雜散光所造成的隨機噪聲;另一方面在圖像處理過程中可以采用平滑濾波、中值濾波等方法減小噪聲對光斑質心的提取誤差,以提高非Scheimpflug條件激光三角測距精度。
4 結論
1) 建立了非Scheimpflug條件下距離測量解析模型,通過定義錐形光束獲得非Scheimpflug條件下光敏面上的能量分布,分析了理論中心位置與質心位置之間的定位誤差,依據距離測量模型解算非Scheimpflug條件下距離測量誤差。
2) 通過對不同非Scheimpflug條件激光三角測距模型定量誤差分析,選擇工作距越大、基線越小、焦距越大的系統參數有利于減小非Scheimpflug條件引入的測量誤差。本文建立的誤差模型及仿真結果,可為非Scheimpflug條件下激光三角測距法應用提供參考。

