融合圖像識別和聚類分析的感應電動機參數辨識
黃 淼,李 濤,文 旭,,文一宇,李國強
(1.重慶郵電大學 自動化學院, 重慶 400065;2.國家電網公司西南分部, 成都 610041;3.西藏電力交易中心有限公司, 拉薩 850000)
0 引言
感應電動機因成本低、可靠性高被廣泛應用,是電力系統負荷中主要的動態元件,對電力系統的運行與控制有著非常重要的影響。許多工程研究,包括電力系統穩定性分析、電壓暫降計算等,都需要合理、準確的感應電動機等效電路模型參數。
在大多數情況下,電動機制造商僅提供設備的銘牌參數等出廠數據,而不直接提供設備的等效電路參數。鑒于此,有必要基于這些數據,通過參數辨識的方法來獲取感應電動機的模型參數。目前,已有不少的相關研究被報道[1-14]。但現有研究在開展參數辨識時,對電動機出廠數據的挖掘仍不夠充分,往往只利用了電動機的銘牌參數。在實際的收資過程中,電機廠家通常還會以圖片格式提供電動機的轉矩倍數—滑差特性曲線和定子電流倍數—滑差特性曲線。
為提高參數估計的準確度,充分利用電動機的出廠數據,通過圖像識別將圖片格式的電動機特性曲線轉化為離散的數據點,在此基礎上對數據集進行聚類簡化[15-16],再將簡化數據集與電動機銘牌參數聯立,從而構建新的參數辨識模型。
1 感應電動機單籠模型
針對感應電動機單籠模型開展研究。模型適用于繞線式和單籠式電動機。如圖1所示,模型等值電路包含6個參數,即定子電阻Rs、定子電抗Xs、轉子電阻Rr、轉子電抗Xr、激磁電阻Rm和激磁電抗Xm。
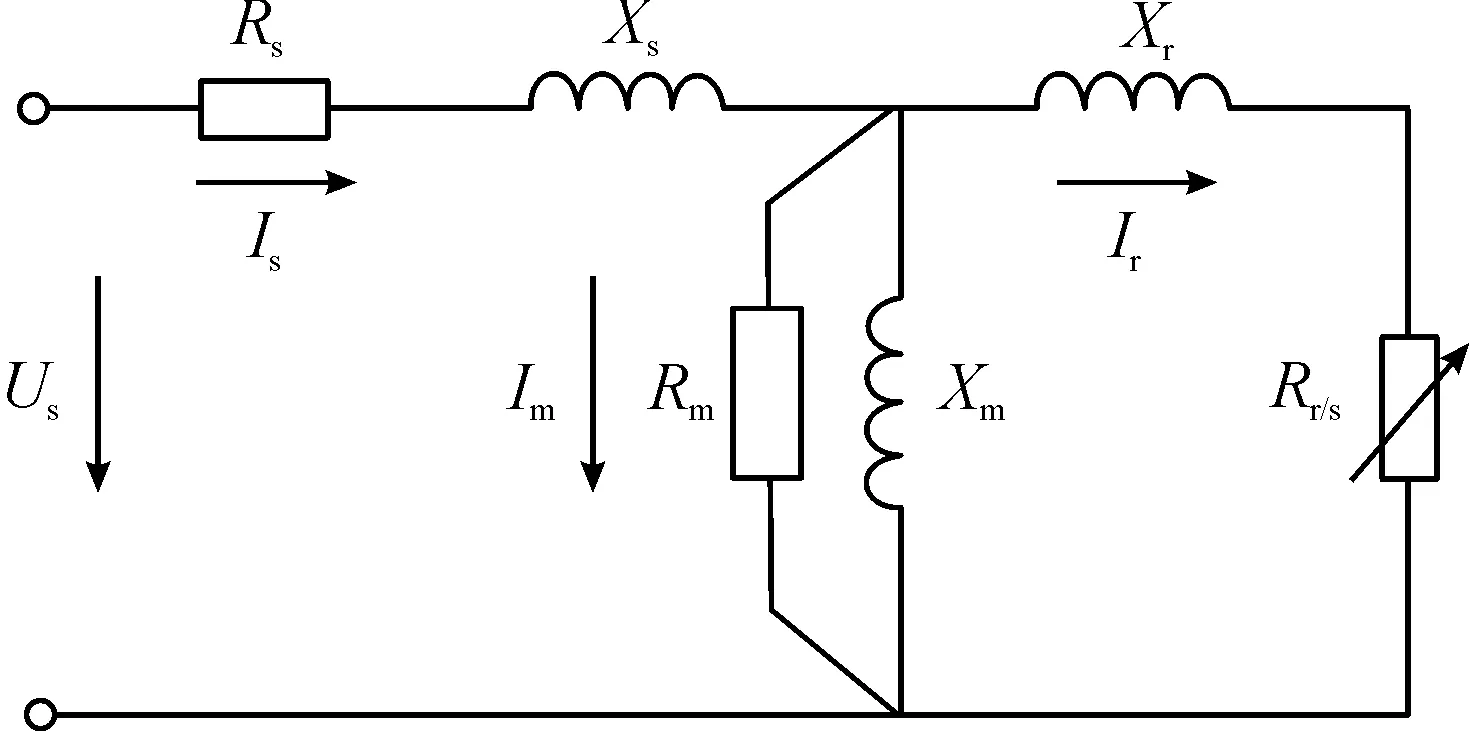
圖1 感應電動機單籠模型等值電路
2 感應電動機參數辨識模型
電動機在出廠時通常會提供銘牌參數、電動機轉矩倍數-滑差和定子電流倍數-滑差特性曲線圖。
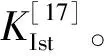
2.1 圖像識別
由于電動機轉矩倍數-滑差和定子電流倍數-滑差特性曲線通常以圖片格式提供,不像銘牌參數可直接利用,因此,運用圖像識別方法對這些特性曲線進行處理,以獲得1個由離散數據點構成的數據集。
圖像識別的具體步驟如下:
步驟1采用式(1)所示的加權平均法,對特性曲線圖進行灰度化處理[18]。
Gray=0.299R+0.587G+0.114B
(1)
式中:Gray為灰度值;R、G、B為圖像紅、綠、藍三原色。
步驟2按式(2)開展二值化處理,將原圖像分割成二值圖像。

(2)
式中:It(x,y)為圖像經二值化處理后的灰度值;I(x,y)為圖像初始灰度值;T為設置的閾值,它可通過最大類間方差法確定[19]。
步驟3設置特性曲線圖的像素范圍和坐標范圍。
步驟4刪除距離坐標軸框較近的數據,以消除坐標軸框和坐標軸刻度對數據集的影響。
步驟5處理特性曲線圖像素較低、曲線較粗的情況。在這種情況下,通過前述步驟得到的數據點橫軸坐標值,可能對應若干個縱軸坐標值。鑒于此,先求取這組縱軸坐標值的均值和標準差,并刪除波動較大的縱軸坐標值,再將剩余縱軸坐標值的均值作為數據點的縱軸坐標[20]。
步驟6保存提取到的離散數據點。
2.2 聚類分析
采用圖像識別技術得到的數據集通常包含大量的離散數據點。若將這些數據都用于后續的參數估計,勢必降低目標函數在尋優時的收斂速度。根據圖2所示的典型曲線可知,在高滑差和低滑差區段內,特性曲線的斜率變化并不明顯,因此考慮先對特性曲線圖進行分段處理,將其劃分為低滑差區段、中滑差區段和高滑差區段,如圖3所示。利用K-means聚類算法對低滑差區段和高滑差區段數據點進行聚類簡化。

圖2 轉矩倍數-滑差和定子電流倍數-滑差特性典型曲線

圖3 特性曲線分段處理結果
K-means聚類算法具有效率高、易實現等優點,其基本思想是通過迭代尋找K個簇中心點使得聚類結果對應的損失函數最小。通常損失函數定義為:
(3)

針對本文問題,若使用K-means聚類后的聚點不在樣本中,則取距離該點最近的樣本點作為聚類結果,從而保證聚點在特性曲線上。
2.3 構建參數辨識優化模型
將電動機出廠銘牌參數與上述數據集聯立,構建的電動機參數辨識優化模型表示為:

(4)
式中:n為聚類后數據集中對應的數據個數;X表示待識別的參數,X=[Rr_estim,Xr_estim,Rm_estim,Xm_estim,Rs_estim,Xs_estim],Xs_estim、Rs_estim、Xr_estim、Rr_estim、Xm_estim、Rm_estim分別為定子電抗、定子電阻、轉子電抗、轉子電阻、激磁電抗和激磁電阻的估計值;Ti和Ii為聚類后數據集中不同滑差對應的轉矩和電流;Testim和Iestim為轉矩和電流的估計值,它們的值會隨著滑差的變化不斷更新;Iin_estim為定子側電流估計值;Zin_estim為總輸入阻抗的估計值;K表示額定功率與相電壓平方的比值,Kestim為K的估計值。
Testim的表達式為:
(5)
式中:Srate為額定轉差率,屬于感應電動機出廠銘牌數據;Ir_estim為轉子側電流估計值。
Srate的表達式為:
(6)
式中:ns為同步轉速;nn為額定轉速,屬于感應電動機出廠銘牌數據。
Ir_estim的表達式為:
(7)
Ze_estim為鐵芯阻抗的估計值,表達式為:

(8)
Iin_estim的表達式為:

(9)
Zin_estim的表達式為:
(10)
Iestim的表達式為:
(11)
Kestim的表達式為:

(12)
由上述可見,所建的參數辨識優化模型屬于非線性模型,適合采用數值穩定性好、收斂速度快的內點法(interior point methods,IPM)進行求解。本文方法在求解時,具體采用原始對偶內點法(primal-dual interior point method,PDIPM)[21-23],其基本思想是:通過引入對偶變量將不等式約束轉化為等式約束,然后求解原始對偶間隙,得到互補條件,從而將原問題轉化為求互補條件的最優解。
綜上所述,感應電動機參數辨識的整體流程如圖4所示。
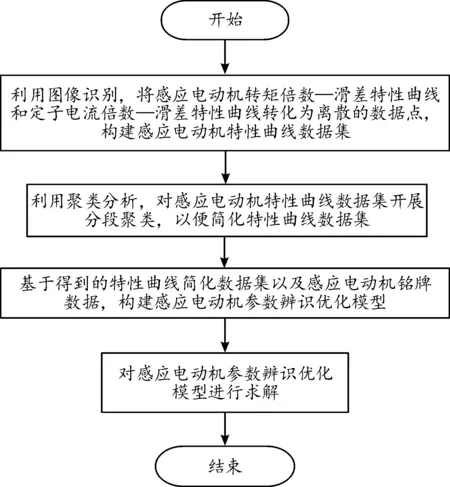
圖4 參數辨識整體流程框圖
3 算例分析
3.1 數據聚類對參數辨識過程的影響
以某臺800 kW電動機為例。在不聚類數據和聚類數據2種場景下開展參數辨識,相應的迭代收斂軌跡如圖5所示。不對數據聚類時,迭代次數高達181次;對數據聚類后,參數求解過程僅迭代了78次。
更多針對不同感應電動機的仿真結果(如表1所示)也表明,采用聚類后的數據集進行參數辨識可有效減少優化算法在參數辨識時的迭代求解次數,提高收斂速度。

圖5 迭代收斂軌跡
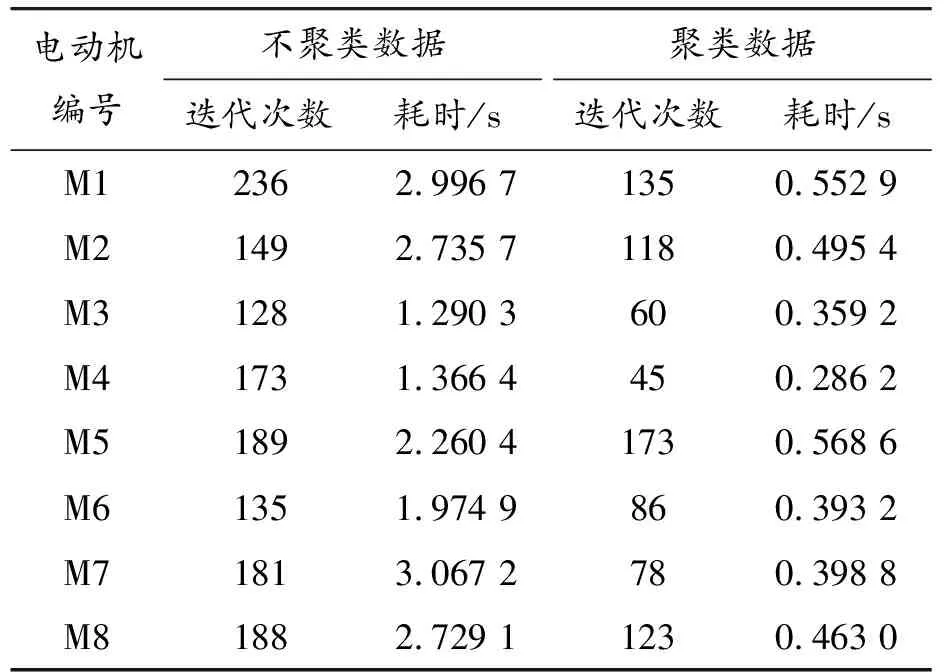
表1 不聚類數據與聚類數據2種場景下的迭代求解情況
3.2 參數辨識效果
8臺不同型號感應電動機的銘牌數據如表2所示。采用本文方法對這些電動機開展參數辨識,結果如表3所示。
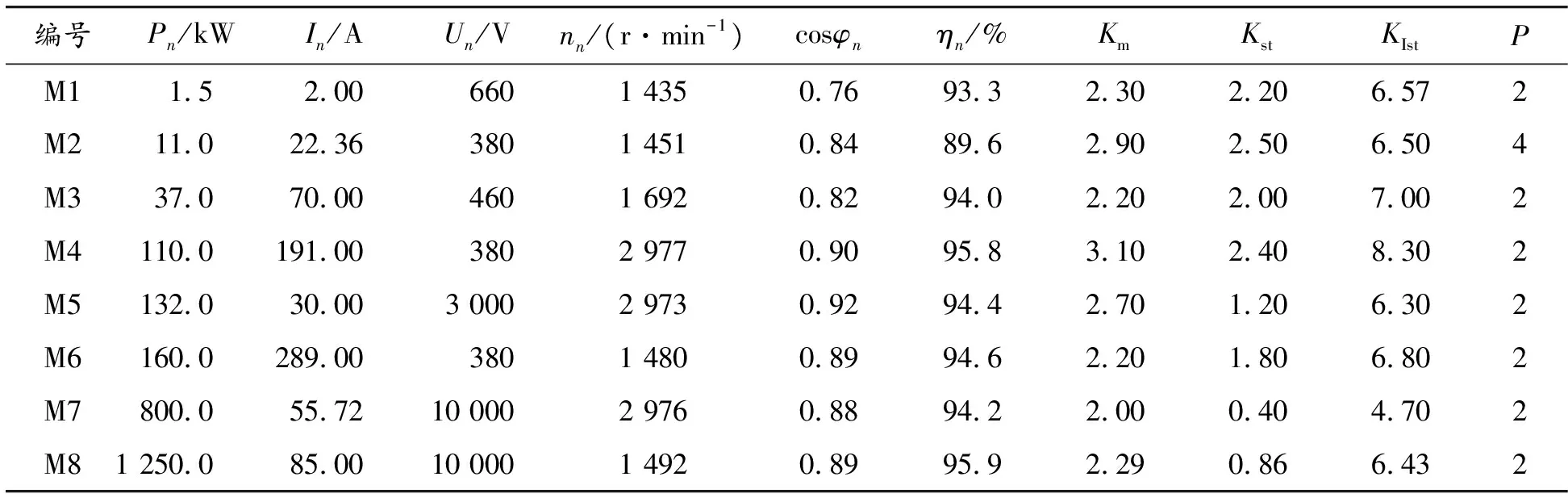
表2 感應電動機出廠銘牌數據 min-1

表3 辨識得到的模型參數
基于表3得到的參數,再計算電動機的額定功率、額定電流、額定功率因數和額定效率等性能指標,相應的計算結果如表4所示。從表4可見,根據參數估計結果計算得到的額定功率等性能指標值,與銘牌參數值趨于一致,這表明辨識得到的等值電路參數能準確反映電動機的工作特性。
將本文方法與文獻[10]所提方法的參數辨識效果進行對比。為便于闡述,記本文方法為方法1,文獻[10]方法為方法2。以容量11、132和800 kW的3臺電動機為例,參數估計結果如表5所示。

表4 性能指標銘牌值與計算值
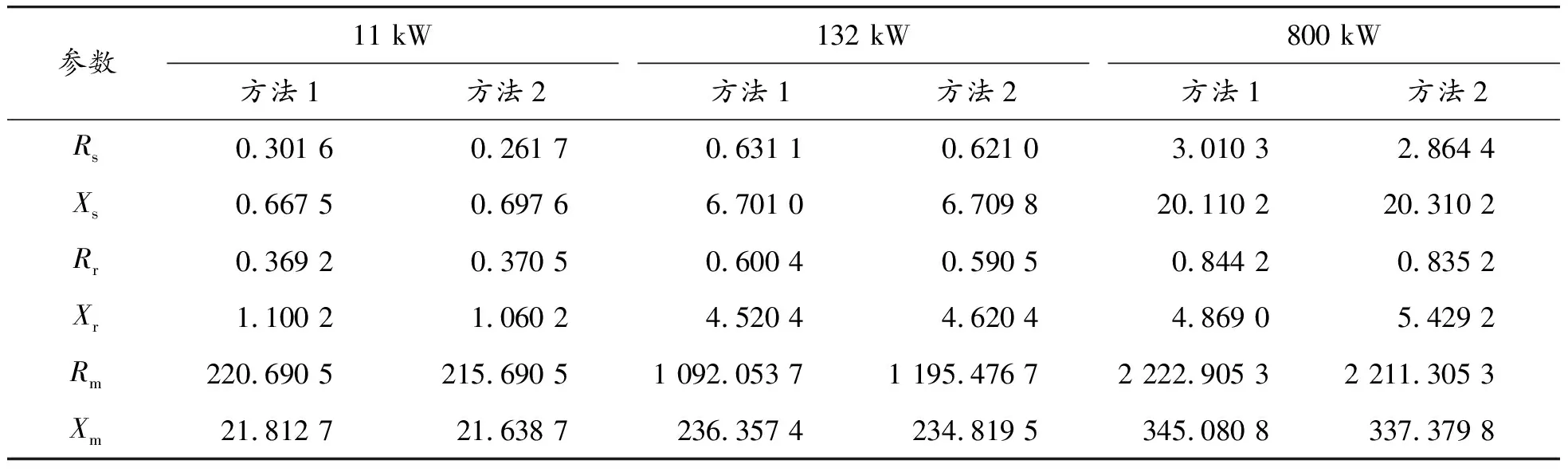
表5 基于2種辨識方法得到的參數估計值
根據參數估計結果計算得到的性能指標值如表6所示。可見,本文方法得到的模型參數能更準確地反映電動機的工作特性。

表6 基于2種辨識方法得到的性能指標值
4 結論
提出了辨識感應電動機單籠模型等值電路參數的新方法。針對現有研究未充分利用轉矩倍數-滑差特性曲線和定子電流倍數-滑差特性曲線的問題,利用圖像識別技術,將圖片格式的特性曲線轉化為離散數據點并進行聚類簡化,在此基礎上結合銘牌數據開展參數辨識。該方法有效解決了電動機參數辨識研究中對出廠數據量利用不充分的問題,聚類分析的引入也提高了參數辨識過程中優化算法的收斂特性。

