基于單元整體教學的作業設計與實施建議
——以“平行四邊形”單元復習為例
?中山市東區松苑中學 張 青
1 問題提出
作業設計是初中數學教學中很重要的一個環節.作業分為課堂作業和課外作業,課堂作業是教學的載體,課外作業是教學活動的延伸.充分發揮作業的功能和價值,讓“小小”的作業發揮“大大”的功能,對于減輕學生課業負擔意義重大.“雙減”背景下作業設計的轉向由“零散”到“整合”,由“工具”到“發展”,從“隨意”到“嚴謹”.以落實核心素養為導向,基于單元整體教學的作業設計應夯實基礎,對“具有某種內在關聯性”的內容進行重組、整合、設計,進而形成相對完整的單元教學作業,構建單元知識體系,實現教學效果最優化.
在初步學習“平行四邊形”之前,學生已經學習了全等三角形、勾股定理等相關知識,本章的學習為后續幾何知識的學習作鋪墊,對于培養學生的邏輯推理能力意義重大.學生對平行四邊形和特殊平行四邊形之間的聯系等容易混淆,為此從整體上設計本單元的作業,以激發學生的學習興趣,發展學生的直觀想象、邏輯推理等學科核心素養,幫助學生整體構建知識之間的聯系.
2 作業設計依據
學習本章知識之前,學生已經熟悉了三角形和梯形的相關知識,了解了三角形的性質,掌握了特殊三角形的性質和判定方法、三角形全等的判定方法、勾股定理等相關數學知識,為本章學習奠定了知識基礎.本節作業設計是單元復習作業,學生雖然初步了解了平行四邊形的性質和判定方法,但是從整體上構建知識之間的聯系較難,不能靈活運用相應知識解決數學問題.本章的學習也為后續二次函數、圓、相似等知識的學習奠定基礎.
3 作業設計目標
立足教材,基于《義務教育數學課程標準》,從整體上設計本章節的作業設計目標:
(1)通過實踐性活動,進一步探索平行四邊形和特殊平行四邊形的性質和判定方法,積累基本的數學活動經驗;
(2)通過變式練習,發展數學思維,構建平行四邊形之間的聯系,培養學生邏輯推理能力;
(3)設計分層作業,由易到難,復習和鞏固平行四邊形的相關知識;
(4)創新作業形式,激發學習幾何的熱情,整體構建數學知識體系.
4 作業設計過程
4.1 立足基礎,設計實踐性作業,積累活動經驗
作業1動手畫兩個全等三角形,并剪下來,將兩個全等的三角形拼在一起,你能拼出什么四邊形?并說說這個四邊形的性質.
設計意圖:從學生熟悉的三角形出發,讓學生在“畫一畫”“拼一拼”“推一推”等數學活動中積累基本數學活動經驗,體會不同類型的三角形可以拼成不同的平行四邊形(如圖1),由三角形的特殊性決定了平行四邊形的特殊性.基于三角形的知識基礎,從研究“特殊三角形”出發,引導學生從邊、角、對角線等角度研究平行四邊形的性質,讓學生學會從一般到特殊的數學歸納方法.

圖1
作業2推一推這些平行四邊形的判定方法是什么?寫一寫它們之間的聯系,并用思維導圖的形式呈現出來.
設計意圖:創新作業形式,通過構建思維導圖,體會特殊平行四邊形之間的區別和聯系,從整體上把握“平行四邊形”的相關知識,查漏補缺,培養邏輯推理能力.
4.2 著眼思維,設計變式練習,落實核心素養
練習1如圖2,在矩形ABCD中,O為對角線BD的中點,過點O的直線分別與AD,BC相交于點E,F,連接BE,DF.
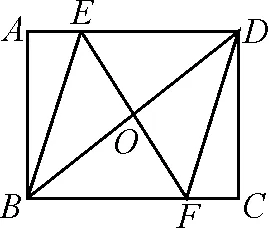
圖2
(1)求證:四邊形BFDE是平行四邊形;
(2)若BD平分∠EBF,求證:四邊形BFDE是菱形;
(3)在(2)的條件下,若BE平分∠ABD,求△ABE與矩形ABCD面積的比值.
變式如圖3,ABCD的對角線AC,BD相交于點O,△OAB是等邊三角形,且AB=2.
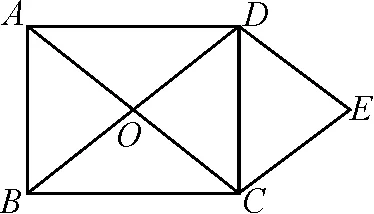
圖3
(3)分別過點C,D作BD,AC的平行線,交點為E,求證:四邊形OCED為菱形;
(4)求四邊形OCED的周長和面積.
設計意圖:通過練習及變式,由淺入深,由易到難,進一步復習和鞏固等邊三角形的性質、角平分線的性質、平行四邊形的性質和判定等知識.在構建平行四邊形、矩形、菱形之間聯系的過程中,培養邏輯推理能力;在完成作業的過程中,提升運算能力,讓學科核心素養真正在完成作業過程中落地生根.
4.3 注重個體,設計分層作業,滿足不同需求
A組練習:(1)在平行四邊形ABCD中,對角線AC,BD交于點O,若使矩形ABCD成為正方形,添加的條件為______;若使菱形ABCD成為正方形,添加的條件為______.
(2)如圖4,在矩形ABCD中,E是BC邊上一點,∠AED=90°,∠EAD=30°,F是AD邊的中點,EF=4 cm,則BE=______cm.
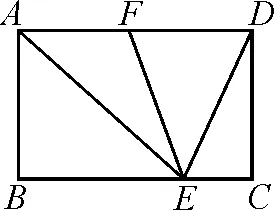
圖4
B組練習:(3)如圖5,四邊形ABCD是矩形,E,F分別線段AD,BC上的點,點O是EF與BD的交點.若將△BED沿直線BD折疊,則點E與點F重合.
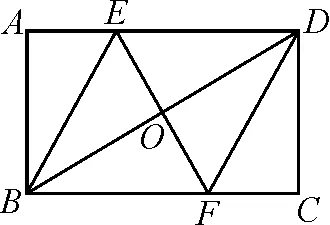
圖5
①求證:四邊形BEDF是菱形;
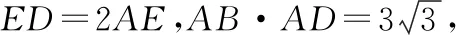
C組練習:(4)如圖6,在正方形ABCD中,AB=2,E為邊AB上一點,F為邊BC上一點.連接DE和AF交于點G,連接BG.若AE=BF,則BG的最小值為______.
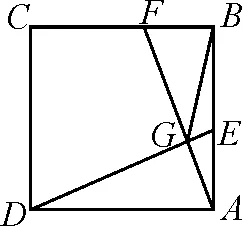
圖6
設計意圖:精心設計分層作業,讓學生根據知識內容自主選擇.分層作業并不是對學生進行分層,分層作業由易到難,基于學生的知識基礎設置開放性問題.A組練習適合基礎薄弱的學生.B組練習有利于學生思維能力的發展,進一步整體構建知識之間的聯系.完成A組練習的學生有種成就感,鞏固基礎同時會進一步嘗試B組練習.C組練習對學生的思維要求較高,可以通過小組合作交流共同完成.在師生交流互動的過程中領悟基本的數學思想方法,提升學生的競爭意識,激發學生學習數學的熱情.
5 實施建議
5.1 作業設計“簡約”而“不簡單”
作業設計不僅僅是以傳統練習的形式呈現,雙減背景下的作業設計要求創新作業形式.教師可以堅持“零起點教學”,從學生熟悉的生活經驗出發,設置“簡約”的作業,讓學生在“做一做”“畫一畫”“說一說”等數學活動中積累基本數學活動經驗,輕松學習數學知識,讓學生愿意學習數學.設計“簡約”作業,要達到“不簡單”的效果,讓學生在掌握“四基”的同時發展“四能”,注重數學思想方法的滲透和核心素養的培養.
5.2 注重“整體性”和“典型性”
課堂作業是教學的載體,課外作業是教學活動的延伸.在作業設計的過程中,教師要充分挖掘例習題的功能和價值.作業設計的轉向由“工具”到“發展”,由“零散”到“整合”,在作業設計的過程中注重目標的“整體性”,從整體的角度把零散的數學知識通過作業聯系起來,構建數學知識之間的聯系,從宏觀的角度去開展作業設計.基于單元整體教學的作業按照“總—分—總”的思路進行設計,區分大單元、中單元、小單元之間的關系,作業設計注重“整體性”和“典型性”.作業不僅僅是“作業”,還承載著“教學”和“課程”的育人功能,作業設計要充分發揮作業的育人價值.
5.3 注重“層次性”和“差異性”
《義務教育數學課程標準(2022年版)》指出:“人人都能獲得良好的數學教育,不同的人在數學上得到不同的發展.”[1]基于單元整體教學的作業設計應注重“層次性”和“差異性”,根據學生的知識基礎和認知規律實施分層作業.分層作業依據學情及教學內容進行編制,由淺入深,由易到難,讓所有學生都可以動筆寫一寫,增強學生學習數學的信心,激發學生學習數學的興趣,讓“人人都能學”“人人都愿學”.
5.4 改善評價方式,評價多元化
改進數學作業的評價方式,不以“分數”和“等級”作為唯一的評價方式.生動的激勵語言可以激發學生的“內在潛力”,例如,“你的方法很不錯”“這個圖畫得真好”等生動的作業評價語言,會帶來不一樣的效果.筆者嘗試采用SK作業分析法,效果顯著.S型錯誤指的是技能(Skill)缺失型錯誤,具體指學生因為審題錯誤、計算出錯等導致沒有做對;K型錯誤指的是知識(Knowledge)欠缺型錯誤,是指知識漏洞導致的出錯.教師可以利用SK作業分析法,找出學生作業出錯的真正原因,有針對性地設計作業,可以達到事半功倍的效果.

