構造直角三角形解答幾何問題的題型分析

?福建省泉州外國語學校 莊菊詠

1 求角度

求解圖形中某一個角的大小是幾何問題中的常見問題之一.這類型問題可以構造直角三角形進行求解，利用直角三角形的特點和性質，結合其他圖形，計算待求角的大小.解答這類問題的具體思路：①分析題意，添加輔助線構造直角三角形；②利用直角三角形的特點(例如直角等于90°)、性質，結合幾何知識求解；③經過邏輯推理計算角的大小.

例1△ABC的BC邊上存在一點P，且PC=2PB，已知∠ABC=45°，∠APC=60°，求∠ACB的大小.

分析:本題存在特殊角∠APC=60°，經過點C作AP的垂線，構造直角三角形CDP，將∠ACB分為兩部分，再根據點P的位置和∠APC的大小進行分析.

解：如圖1,過點C作CD⊥AP，垂足為D，連接BD.

圖1

在Rt△CDP中，

∵∠APC=60°，

∴∠DCP=30°.

∴PC=2PD.

∵PC=2PB，

∴PB=PD.

∴∠PBD=∠PDB=30°.

又∵∠ABC=45°，

∴∠DAB=∠DBA=15°.

∴BD=AD=CD，∠ACD=45°.

∴∠ACB=45°+30°=75°.

2 求線段的長

求解圖形中某一線段的長是幾何圖形中的常見問題，有時可以通過構造直角三角形求解，利用直角三角形的特殊角和對應的三角函數值，并結合相關定理(勾股定理、射影定理等)求解線段長度.解答這類問題的具體思路為：①根據題意構造直角三角形，并確定其內角的大小；②利用特殊的三角函數值或對應的定理列式求解，計算所求線段的長度.

例2在△ABC中，D是AC邊上一點，若BD⊥AB，∠ABC=120°，AB=CD=1，求AD的長.

分析:如圖2所示，本題需要從點B入手再構造一個直角三角形，通過比例關系和勾股定理解得線段AD的長度.

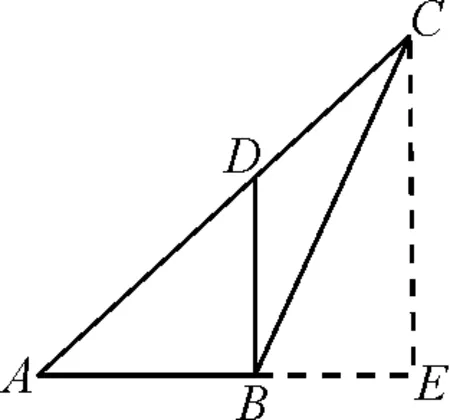
圖2

解：過點C作CE⊥AB，與AB的延長線交于點E.

又DB⊥AB，所以BD∥CE.

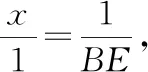
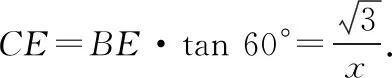
等價于：(x+2)(x3-2)=0.

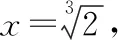
3 求面積

求解某個圖形的面積大小是幾何中的常考問題.這類型問題有時可以構造直角三角形求解，一般將原問題轉化為求解直角三角形的面積問題，利用直角三角形的面積公式進行計算.解答的具體思路為：①分析圖形特點，通過輔助線等手段構造直角三角形；②根據題意分析直接或間接計算面積，并確定相關線段的長度；③利用幾何圖形的面積公式計算求解.

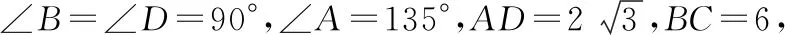
分析:由題意可知，四邊形ABCD是不規則圖形，其面積需要利用添補法求解.如圖3所示，將其添補為一個直角三角形，并利用直角三角形的面積公式間接求解.

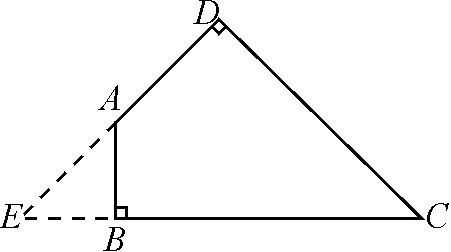
圖3

解：設DA,CB的延長線交于點E,由題意可得，四邊形補為Rt△EDC，如圖3所示，且△EAB和△EDC都是等腰直角三角形.

在Rt△EDC中，

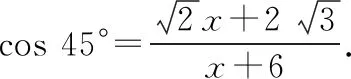
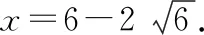
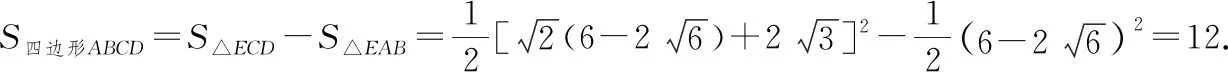
4 求最值

最值問題是幾何中的一類常考問題，一般為求線段的最值或角度的最值，有時可以利構造直角三角形求解.解答的具體思路為：①根據題目特點構造直角三角形；②將待求角或待求線段與直角三角形建立聯系；③利用直角三角形的知識分析待求最值.

例4在△ABC中，BC=5，AC=12，AB=13，在邊AB，AC上分別取點D，E，使線段DE將△ABC分為面積相等的兩個部分，試求這個線段的最短長度.

分析:利用勾股定理的逆定理可知△ABC為直角三角形.過點D作△DEA的高DF，將原問題轉化為求解直角三角形的問題.

解：由BC=5，AB=12，AB=13,結合勾股定理的逆定理，可得△ABC是直角三角形，且AC⊥BC.

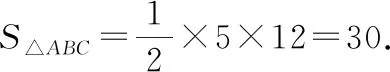
又因為線段DE將△ABC分為面積相等的兩個部分，所以S△DEA=15.

過點D作△DEA的高DF，交AC于點F，如圖4,則DF∥BC.

圖4

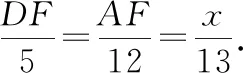
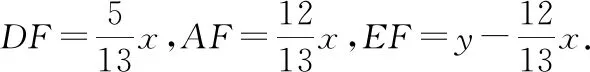
在Rt△DEF中，由DE2=EF2+DF2，得

又由S△DEA=15，得xy=78.

所以DE2=(x-y)2+12.

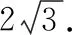
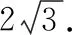
5 作證明

證明題是幾何中必不可少的一類問題，證明形式包括求證角度的大小或關系，求證線段的長度或關系等，構造直角三角形是解答幾何證明題常用的有效手段.具體思路為：①根據題意分析題目特點，構造直角三角形；②利用直角三角形的角度關系或邊長關系，將待證明的線段或角與直角三角形建立聯系；③最后利用直角三角形的相關知識求證即可.

例5已知點M是Rt△ABC斜邊BC的中點，點P，Q分別在邊AB，AC上，且PM⊥QM.

求證：PQ2=PB2+QC2.

分析:本題中QC與PQ，PB沒有直接關系，要想證明PQ2=PB2+QC2成立，就需要構造直角三角形，將這三條邊之間建立聯系，且PQ為斜邊，如圖5所示.

圖5

證明:延長QM至點N，使MN=QM，連結PN，BN，如圖5所示.

∵PM⊥QM，

∴PQ=PN.

又∵M是BC的中點，

∴△BMN≌△CMQ.

∴BN=QC，∠MBN=∠C.

∴BN∥AC.

∴∠PBN=∠A=90°.

∴PN2=PB2+BN2.

故PQ2=PB2+QC2成立.

本文中介紹的幾種題型都是常見的利用直角三角形求解的幾何問題.直角三角形對求解幾何問題有重要作用，能有效降低題目難度，化繁為簡.解題時要學會靈活構造直角三角形,除此之外，還要熟練掌握直角三角形的性質及面積公式等基礎知識，確保萬無一失.