例析勾股定理常見的應用類型

?甘肅省武威市天祝藏族自治縣新華中學 趙 霞

1 引言

勾股定理在生活中的應用比較普遍，大致可歸類為求邊長，求最短路程，求解折疊問題，等等.下面結合幾道例題對勾股定理常見的應用類型及解決策略作分析和探究.

2 利用勾股定理求邊長

例1如圖1所示，在直角三角形ABC中，∠ABC為直角，且AB=16 m.正方形BCEF的周長為48 m，BD⊥AC于點D.求BD的長.

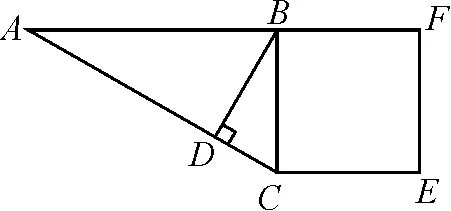
圖1

分析：本題是非常典型的“三垂直”問題，可用等面積法和方程法解決.無論用何種方法，都需先根據“正方形BCEF的周長為48 m”求出BC=12 m，然后根據勾股定理將AC的長求出.

方法二(方程法)：首先，設AD=xm，那么CD=(20-x) m.由于BD⊥AC于點D，所以△ABD和△BDC都是直角三角形.在Rt△ABD中，BD2=AB2-AD2；在Rt△BDC中，BD2=BC2-DC2.于是，就得到了AB2-AD2=BC2-DC2，進而得到方程162-x2=122-(20-x)2，解得x=12.8 m.然后利用BD2=AB2-AD2得到BD的長為9.6 m.

方法總結：利用勾股定理求圖形的邊長，常用的有等面積法和方程法，在實際解題中都非常適用，且通常前者更簡單[1].等面積法多用于“三垂直”問題，而方程法多用于非直角三角形中，以求高問題最為典型[2].

3 利用勾股定理進行證明

例2如圖2所示，圖形ABFC為一任意四邊形，且AB⊥CB，垂足為B；CD⊥AD，垂足為D，AD2=2AB2-CD2.

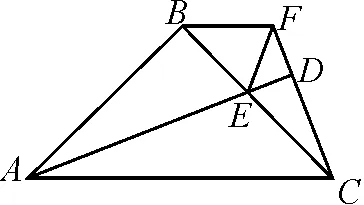
圖2

求證：AB=BC.

分析：本題中的“AD2=2AB2-CD2”條件比較復雜，容易讓學生產生畏難心理.事實上，仔細觀察便可以發現，該條件與勾股定理聯系非常緊密.所以，只需找到圖中與勾股定理有關的“線索”，然后利用勾股定理進行轉換.

在Rt△ABC中，由勾股定理，可得AC2=AB2+BC2；在Rt△ACD中，由勾股定理，可得AC2=AD2+DC2.于是，就有AB2+BC2=AD2+DC2，即AD2=AB2+BC2-DC2.由于AD2=2AB2-CD2，于是得到2AB2-CD2=AB2+BC2-DC2，由此進一步得到2AB2=AB2+BC2，即AB2=BC2，因此證得AB=BC.

方法總結：當題中邊之間的數量關系非常復雜時，學生首先不能有畏難心理，應嘗試著從復雜的條件中找到“提示”，進而找到解題的突破口.

4 利用勾股定理求解最短路程問題

例3如圖3，是一個透明的長方體魚缸，AD為80 cm，AB為60 cm，水深AE為40 cm.在水面上緊貼內壁G處有一滴蜂蜜，G在水面線EF上，且EG為60 cm.一只小螞蟻想從魚缸外的A點沿外壁爬到魚缸內壁G處吃蜂蜜，求小螞蟻爬行的最短路線長度.

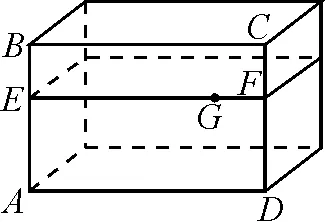
圖3

解析：本題是常見的幾何體表面上最短路程問題，但與以往不同的是“蜂蜜”G點不在外壁，而在內壁，于是小螞蟻的運動路線分為外壁和內壁兩部分.要使得小螞蟻爬行的距離最短，則需這兩部分的路線在一條直線上，于是就需要作A點關于BC的對稱點A′.

首先，如圖4所示，作點A關于BC的對稱點A′，連接A′G且交BC于點O.根據對稱性質，可得A′O與OA相等，即線段OA為小螞蟻在外壁爬行的最短路線.而OG就是小螞蟻在內壁爬行的最短路程，它與A′O正好在同一直線上.因此，小螞蟻爬去吃蜂蜜最短的路程就是線段A′G.在Rt△A′EG中，根據勾股定理得到A′G的長為100 cm.

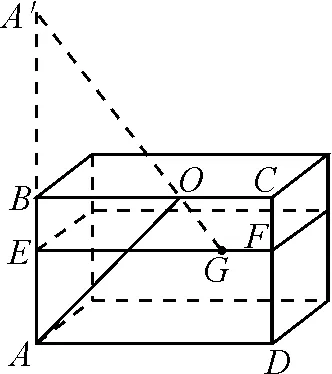
圖4

方法總結：“蜜蜂問題”是勾股定理中常考的題型，分內壁和外壁兩種.如果將蜂蜜從外壁移至內壁，求最短路程的方法其實并未改變，仍然是根據對稱性作圖，找到點的對稱點，然后求解.為了便于理解，學生應首先作出相應的圖形，然后靈活利用相關性質解題.

5 利用勾股定理求解折疊問題

例4如圖5，長方形ABCD中，長AB為8，寬BC為6，P是AD上的一點，現將△ABP沿著BP折疊，PE和CD相交，BE與CD相交，交點分別為O，G，且OD=OE.求線段AP的長.

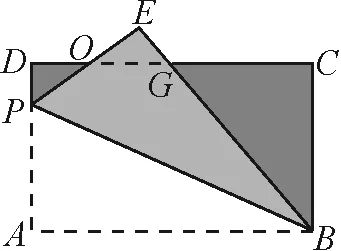
圖5

解析：本題是典型的折疊問題，根據折疊性質可得到對應角相等、對應邊相等[3].既然本題要求AP的長，那么不妨設AP=x，于是將相應的線段用含有x的代數式表示出來后，將它們放入一個直角三角形中，然后根據勾股定理得到方程并解之，即可求出線段AP的長.

由題意可得△ABP≌△EBP，然后證明△ODP≌△OEG.于是，得到OP=OG，PD=GE，由此進一步可得DG=OD+OG=OE+OP=EP.此時，不妨設AP=EP=x，則PD=GE=6-x，DG=x，CG=8-x，BG=2+x.在Rt△BCG中，由勾股定理，可得62+(8-x)2=(x+2)2.解得x=4.8，即線段AP的長為4.8.

方法總結：使用勾股定理解決折疊問題，要注意以下幾個方面：

(1)根據折疊性質先得出對應點、對應線段之間的位置、大小關系，它們都分別不變.

(2)緊緊抓住題中所給的點、線，想法構造出一個直角三角形[4].

(3)在構造的直角三角形中，利用勾股定理列方程計算.當然，有時也只需直接計算即可.

6 勾股定理應用類型解決思路總結

通過以上分析可以發現，勾股定理的應用類型非常豐富，且解決思路靈活多變.要想學好并應用好勾股定理，筆者認為要從以下幾個方面出發：

首先，夯實基礎，在“熟”的基礎上“巧”.所謂“熟能生巧”，就是在熟練掌握的基礎上巧妙解決問題.所以，平時教學和訓練中，教師可根據上述幾種類型對學生進行針對性訓練，并作適當拓展，讓學生對勾股定理及其逆定理有更深刻的感悟.

其次，重視思維，在“常”的基礎上“變”.制約學生應用勾股定理解決問題的一個重要因素是思維受限.為此，在平時的教學與訓練中，教師可對上述每一個類型進行變式，或激發學生利用“一題多解”解決問題.這樣一來，不僅讓問題得到了有效延伸，也讓學生的思維更加靈活.

7 結語

總而言之，勾股定理及其應用在初中幾何部分占據著非常重要的地位，在知識的考查形式上變化多樣，本文中只選擇了幾種具有代表性的問題加以分析.作為初中數學教師，一方面要不斷加強這方面知識體系的構建，讓學生思維變得更靈活，另一方面要勤于發現和總結，不斷提高自身的分析和研究能力.只有這樣，才能將更多、更好的方法傳授給學生.