基于X射線斷層掃描的小麥籽粒模型構建及離散元參數標定

朱 康， 惠延波， 周 穎， 王宏曉， 張云龍， 李 輝， 陳艷雷， 鄭金鋒， 白路遙

(河南工業大學先進制造研究所，鄭州 450001)

離散元法又稱離散單元法，是一種用于模擬并分析散體介質系統動力學行為的數值方法，廣泛應用于地質工程、土木工程、農業工程[1]。在農業工程中，農業裝備會涉及到大量的谷物顆粒的運動，運用離散元法研究兩者之間的相互作用關系，可以優化農業裝備的機械結構、提升裝備工作效率，為現代農業裝備的數值化設計提供理論基礎[4]。

在進行離散元仿真時，模型的精度和仿真參數的設置會對仿真結果產生較大的影響[11]。劉凡一等[9]使用游標卡尺測量小麥籽粒的平均長軸、短軸，將小麥近似地看作規則的橢球型，在EDEM中采用5球組合的方式構建小麥離散元模型對小麥離散元參數進行了標定，但在實際中，小麥籽粒形狀是不規則的，通過數量較少的球形顆粒的堆疊，無法準確地反映小麥籽粒的真實輪廓。趙武云[10]對玉米種子進行切片，每片厚度約為1 mm，采集玉米種子剖面圖像，根據剖面圖像提取種子外輪廓樣條曲線，在SolidWorks中進行輪廓曲線放樣繪制玉米種子三維模型，但切片數量過少，無法完整地表示玉米的輪廓特征。張榮芳等[11]借助三維掃描和逆向工程的方法獲取水稻種子外形輪廓，構建不同半徑的填充球離散元模型對種間靜摩擦因數和動摩擦因數進行了標定，但三維激光掃描儀針對尺寸較小的物體掃描的精度較低，無法完整地獲取物體三維輪廓。

因此，本實驗以小麥為研究對象，基于X射線斷層掃描技術獲取1 024張不同灰度值的二維切片，采用圖像濾波、圖像分割等算法構建出小麥籽粒的三維外輪廓模型；在EDEM中導入外輪廓模型，分別填充4種不同數量的球(17、49、80、126球)來擬合小麥籽粒的真實形狀，構建了更加精準的小麥籽粒離散元模型；通過休止角實際實驗與EDEM仿真實驗，運用Plackett-Burman實驗、最陡爬坡實驗、響應面優化實驗標定了小麥離散元仿真參數；最后對標定的參數進行仿真分析并與實際實驗進行對比，驗證了本方法構建的離散元模型標定參數的準確性，為其他不規則谷物模型的構建提供了參考。

1 小麥籽粒模型構建

1.1 實驗材料

實驗材料選取豐德存麥5號，含水率12.5%。

1.2 圖像采集

采用YXLON Y.Cheetah型微米X射線斷層掃描系統(Micro-CT)采集小麥籽粒三維灰度圖像，如圖1所示。隨機選取外形尺寸完好的小麥籽粒，通過X射線斷層掃描系統對其進行掃描，單顆籽粒1次掃描約20 min，可以無損地獲取小麥籽粒的1 024張二維灰度圖像。

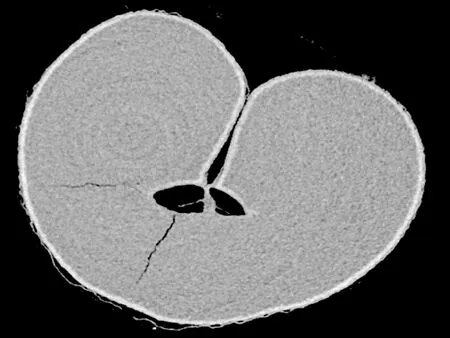
圖1 二維灰度圖像

1.3 圖像重構

從二維灰度圖像可以看出，小麥籽粒的不同組織對X射線的吸收不同，呈現的灰度值也就不同，因此可以有效地區分各組織的輪廓[12]。通過二維灰度圖像的堆疊，可完整地構建出小麥籽粒輪廓。采用非局部均值濾波算法，去除圖像噪聲，提高圖像質量；采用交互式閥值分割算法分離出小麥籽粒的外輪廓組織，如圖2所示；最后基于體繪制及面繪制方法重構出小麥籽粒三維外輪廓模型。構建好的三維模型存在表面粗糙、孔洞等問題，將三維模型轉化為點云格式導入Geomagic Design中進行孔洞的填補、表面光滑處理等操作，最終生成實體模型[13]，如圖3所示。

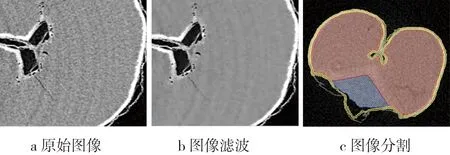
圖2 圖像處理

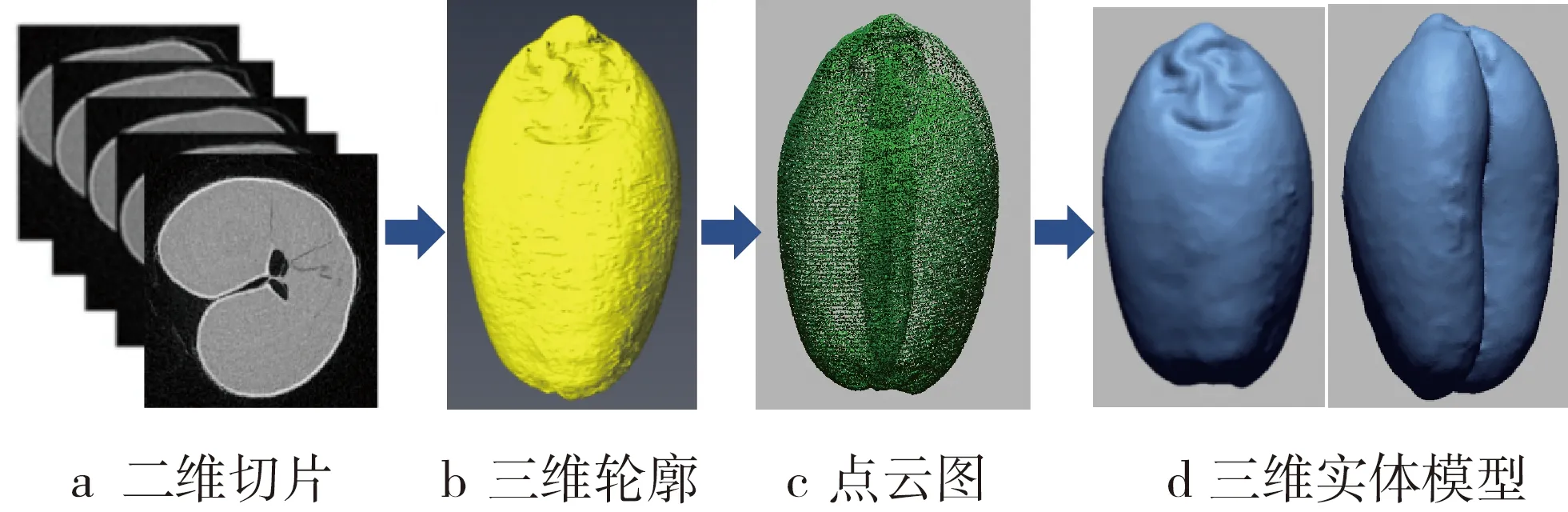
圖3 小麥籽粒模型構建

1.4 離散元模型構建

將X射線斷層掃描方法構建的小麥籽粒外輪廓模型導入EDEM中，以此為基礎擬合小麥籽粒的真實形狀，構建出17、49、80、126球組合的小麥籽粒仿真模型，如圖4所示。

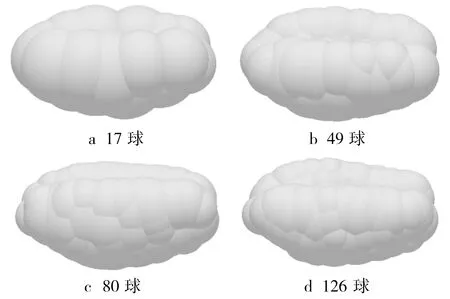
圖4 小麥籽粒離散元仿真模型

2 離散元仿真參數標定

2.1 休止角實際實驗

休止角是物料由高處滑落至平面上堆積形成的錐體的斜面與水平面之間的夾角，是表征顆粒流動、摩擦特性等特性的宏觀參數[14]。運用離散元法研究的谷物的休止角，可以掌握谷物堆積形成糧堆的機制，了解顆粒與顆粒、顆粒與裝備的之間的力學特性。

本次離散元參數標定采用休止角實驗與離散元仿真實驗結合的方法，實驗方法參照GB/T 16913—2008，實驗裝置如圖5所示，由無底圓筒(長度120 mm，內徑40 mm)、有機玻璃板(150 mm×150 mm)、實驗臺組成。無底圓筒與底面有機玻璃板重合，將小麥填滿無底圓筒后，以0.02 m/s的速度向上勻速提升圓筒，小麥自然落下并在底面堆積，錐面與底面之間的夾角即為休止角，每組實驗重復5次。采集籽粒堆積的8個方向的圖像，使用Matable讀取采集的圖像，對圖像進行二值化、邊緣提取、邊緣直線擬合來測量小麥堆積的休止角[15]，如圖6所示。對采集的數據去除極值，取其平均值，最終測得實際休止角為20.326 5°。

注：1.實驗臺 2.小麥 3.無底圓筒 4.有機玻璃板。圖5 小麥休止角實驗

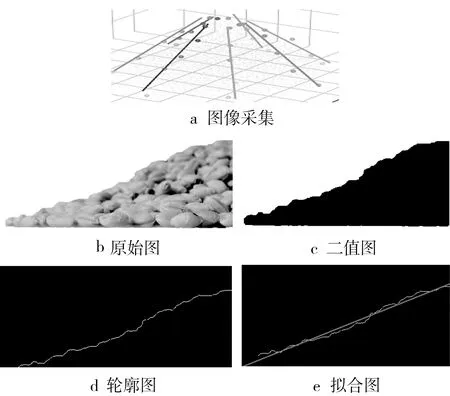
圖6 Matable圖像處理

2.2 休止角仿真實驗

2.2.1 仿真參數

本次實驗所需的仿真參數如表1所示[16]。

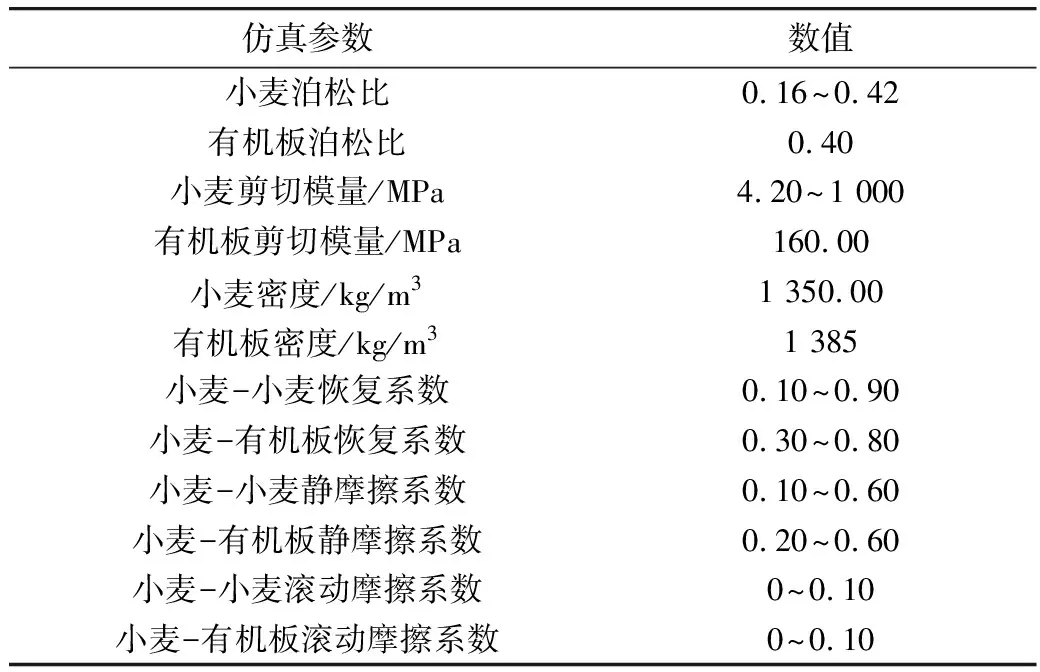
表1 小麥離散元仿真參數

2.2.2 仿真實驗

為縮短仿真時間，休止角仿真實驗選用17球小麥模型，在EDEM中構建長120 mm、內徑40 mm、上下開口的圓筒。在圓筒頂端以5 000顆/s的速度隨機生成小麥顆粒直至填滿圓筒，等待顆粒穩定，此過程時間為1 s；隨后以0.02 m/s的速度向上提升圓筒，直至顆粒全部落下并形成穩定的堆積體，此過程過程仿真時間為3 s，如圖7所示。仿真模型選用Hertz-Mindlin (no slip)接觸模型，時間步長為20%，仿真總時長為5 s。

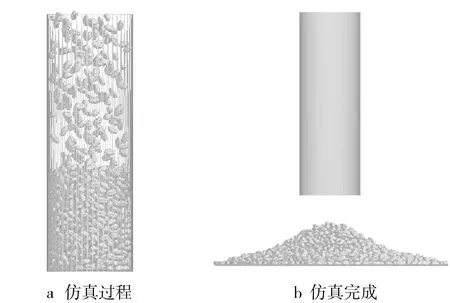
圖7 小麥籽粒休止角離散元仿真

2.3 參數標定

2.3.1 Plackett-Burman實驗

在Plackett-Burman實驗設計的基礎上，以小麥籽粒的休止角為響應值，選取影響小麥籽粒休止角的八個參數進行評價，篩選出影響小麥休止角的顯著因素[19]。每個因素取低水平(-1)和高水平(+1)2個水平，共12組實驗，如表2所示。

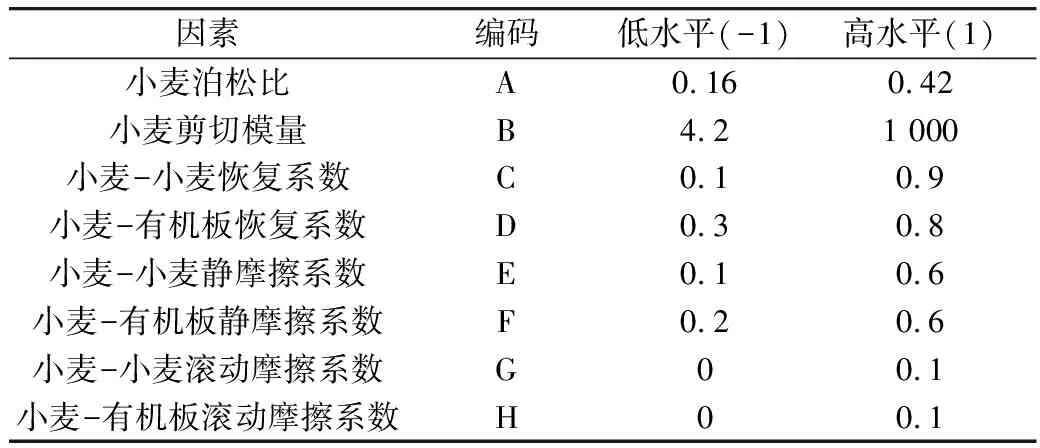
表2 Plackett-Burman實驗設計的因素水平及編碼

Plackett-Burman實驗設計及結果如表3所示。運用Design-Expert軟件進行求解得到的結果如表4所示。根據各因素的P值大小判斷出影響小麥休止角的關鍵因素依次為：E(小麥-小麥靜摩擦系數)>G(小麥-小麥滾動摩擦系數)>F(小麥-有機板靜摩擦系數)。其中小麥-小麥靜摩擦系數、小麥-小麥滾動摩擦系數及小麥-有機板靜摩擦系數均達到極其顯著水平。在后續的最陡爬坡實驗中只考慮這3個參數的影響，結合其他仿真參數進行最陡爬坡實驗和響應面優化實驗。

表3 Plackett-Burman實驗設計及結果

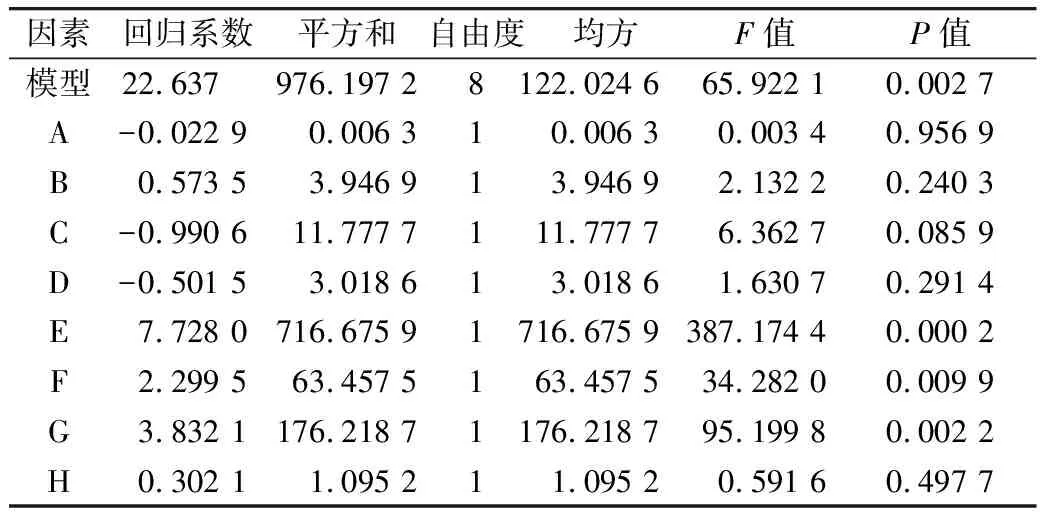
表4 Plackett-Burman實驗設計各因素效應評價

2.3.2 最陡爬坡實驗

基于Plackett-Burman實驗篩選出較顯著的參數，設計最陡爬坡實驗來快速逼近各顯著參數的最佳區域。根據小麥-小麥靜摩擦系數、小麥-小麥滾動摩擦系數和小麥-有機板靜摩擦系數3個因素的效應大小設計相應的步長，實驗設計及結果如表5所示。在第二組時，休止角的相對誤差最小，因此選擇第二組為水平中心點，第一組為低水平，第三組為高水平進行響應面優化實驗。

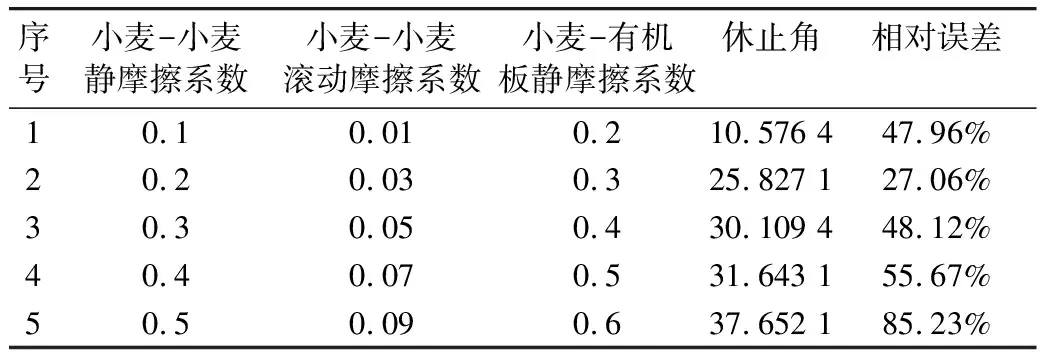
表5 最陡爬坡實驗設計及結果

2.3.3 響應面優化實驗

根據Plackett-Burman和最陡爬坡實驗結果，以小麥-小麥靜摩擦系數、小麥-小麥滾動摩擦系數和小麥-有機板靜摩擦系數為自變量，休止角θ為因變量建立三因素三水平實驗，如表6所示。

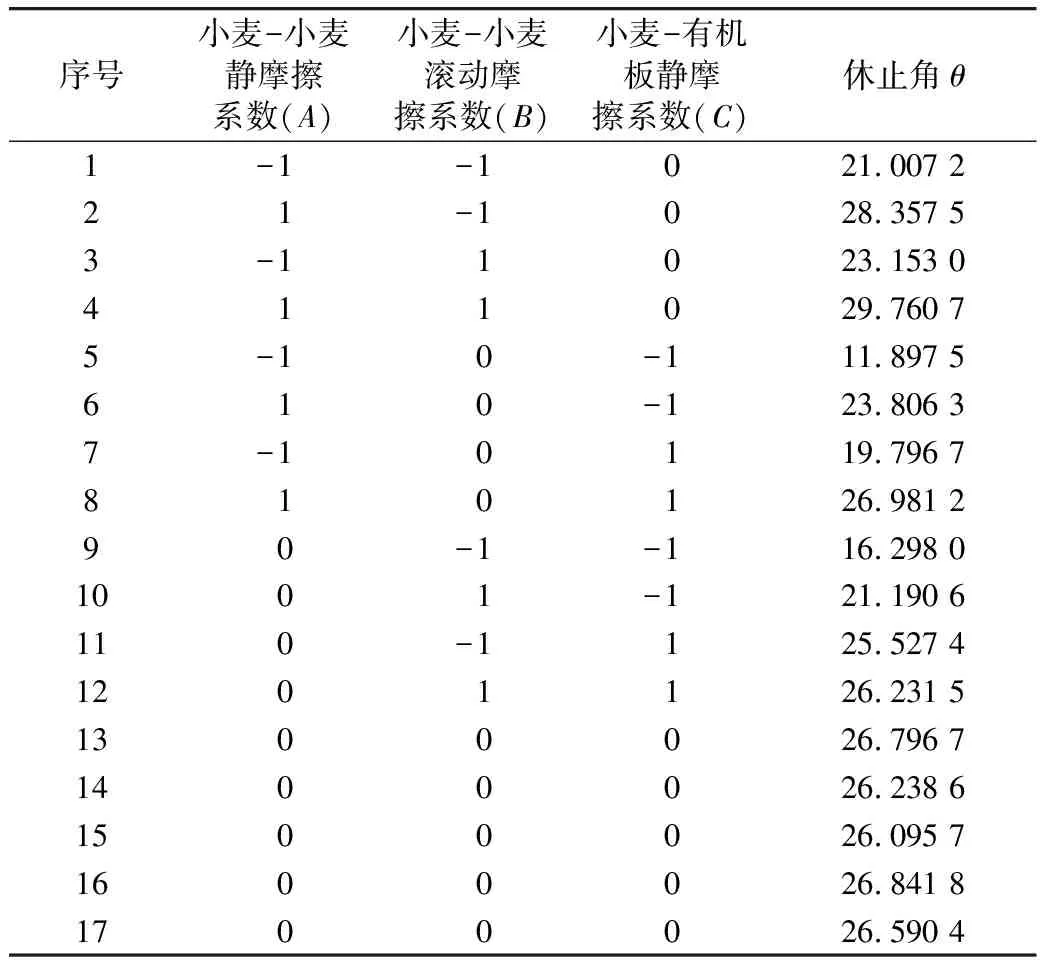
表6 Box-Behnken實驗設計及結果

通過Design-Expert求解得到休止角與3個顯著參數的二次多項式回歸模型為：

θ=26.51+4.13A+1.14B+3.17C-0.19B-1.18AC-1.05BC-1.32+0.37B2-4.57C2

式中：θ為休止角；A為小麥-小麥靜摩擦系數；B為小麥-小麥滾動摩擦系數；C為小麥-有機板靜摩擦系數。

回歸模型方差分析結果如表7。其中，回歸模型P<0.000 1(極其顯著)，失擬項P=0.52>0.05(不顯著)，說明該回歸模型可靠，擬合程度高。由A、B、C的P值可判斷出：三者對休止角的影響都極其顯著。此外，模型的決定系數R2=0.983 8，說明回歸方程相關性較好；校正決定系數adjR2=0.962 9，說明預測值與實際值具有較高的相關性；變異系數CV=3.72%，說明模型合理。此模型可用于對休止角的影響因素進行分析。

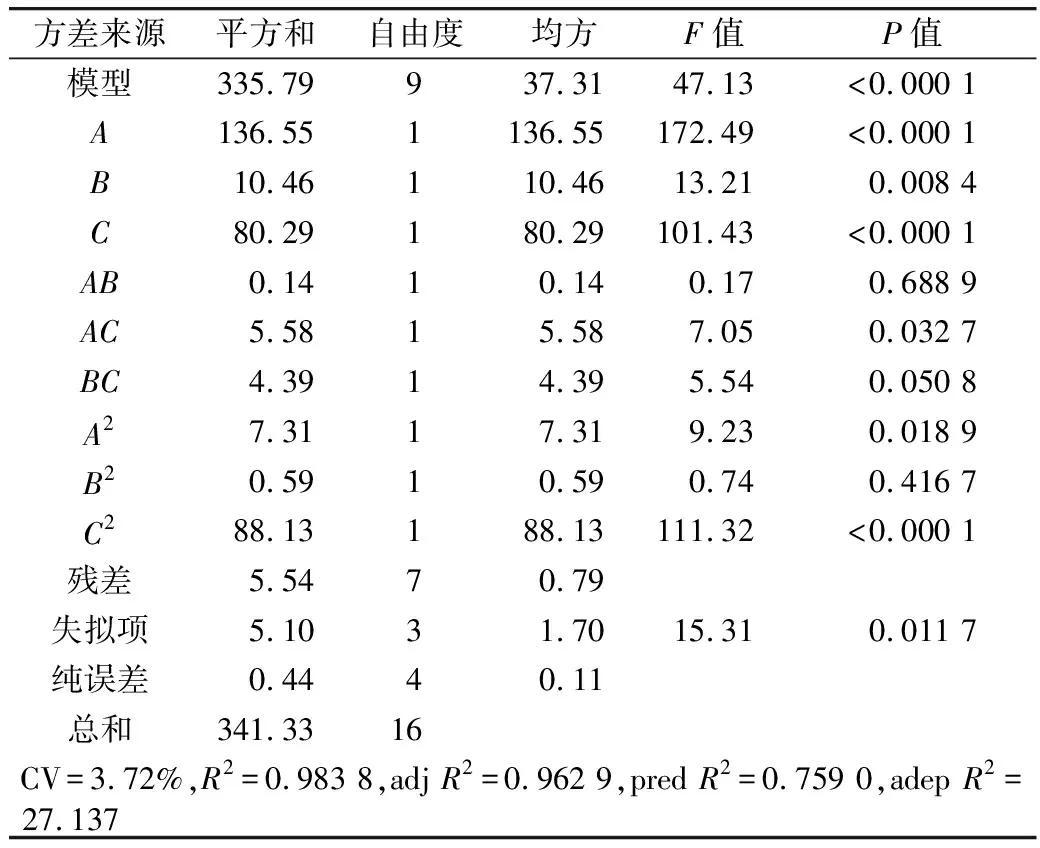
表7 回歸模型方差分析結果

運用Design-Expert中的Optimization功能，以實際休止角為目標值，求解得到最優參數為小麥-小麥靜摩擦系數為0.185、小麥-小麥滾動摩擦系數為0.046、小麥-有機板靜摩擦系數數為0.203。

3 驗證實驗

分別用構建的4種小麥籽粒模型對標定的離散元參數進行仿真，并于實際實驗進行對比分析，得到的仿真結果結果及相對誤差如表8所示。從表8中可以看出，4種模型的仿真結果相近，與實際休止角的相對誤差小于1.30%，表明本文基于X射線斷層掃描方法構建的模型、標定的參數可用于離散元仿真。

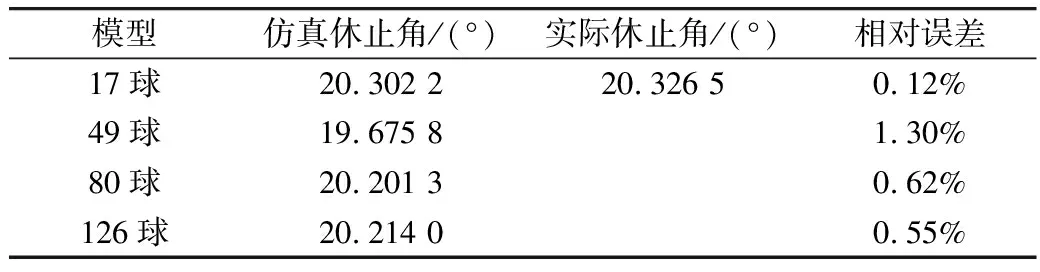
表8 實驗驗證結果

4 結論

基于X射線斷層掃描技術，運用圖像濾波、圖像分割等算法重構了小麥籽粒的外輪廓模型；在EDEM中，分別填充4種不同數量的球(17、49、80、126球)來擬合小麥籽粒的真實形狀，構建了更加精準的小麥離散元模型。

基于X射線斷層掃描技術構建的離散元仿真模型，通過休止角實驗與離散元仿真實驗結合，運用Plackett-Burman實驗、最陡爬坡實驗、響應面優化實驗，標定了小麥離散元仿真所需要的參數；用構建的4種小麥籽粒模型對標定的離散元參數進行仿真分析并與實際實驗進行驗證，結果表明本文方法構建的離散元模型及標定的參數可用于離散元仿真。