無車承運人平臺線路定價模型研究

李佳駿，王永忠，王楷文，張啟凡，萬連成

(中國民用航空飛行學院 空中交通管理學院，四川 廣漢 618307)

隨我國無車承運行業的逐步興起，承運線路的科學問價是眾多無車承運人平臺亟待解決的問題.無車承運人[1]是以承運人身份與托運人簽訂運輸合同，自愿按合同承擔承運人的責任與義務，通過無車承運人平臺委托實際承運人完成運輸任務的道路貨運經營者.該平臺具有網絡效應明顯、資源整合能力強、品牌效應廣等特點，利用互聯網手段和組織模式創新，有效促進貨運市場的資源集約整合和行業規范發展，對于促進物流貨運行業的轉型升級和提質增效具有重要意義[2].國內的無車承運模式主要由貨主、無車承運人平臺和承運人組成.由貨主通過平臺發單，經平臺信息匹配后由車主接單并進行實際的運輸任務.

從無車承運人的視角來考慮，面向廣大擁有運力資源的承運端司機.司機參考承運路線任務發布的價格并以此決定是否要承運此運輸任務.為保證任務的承運，平臺會采取動態定價的方式，若任務未被接單承運，將帶來一定損失.如果在一段規定時間內，司機未有接單，則這條路線可以進行適度調價.每條線路任務最多允許發布3次價格，首次發布之后仍可進行兩次刷新[3].快速成交和較低的承運成本是無承運人平臺當前最關注的目標.

為快速成交和降低承運成本，首先應當解決無車承運人平臺的定價問題.文中通過定量分析的方法，欲探索影響無車承運人平臺進行運輸線路定價的主要因素.利用數理統計的方式來分析這些問題，對這些因素進行相關性的分析并降維，確定影響定價的因素.

根據前期收集的數據，建立對成交貨運路線歷史交易數據中的定價進行評價的數學模型.對歷史交易數據的定價進行評價，需要找出與定價最相關的指標，使用這些指標再利用評價算法來建立所需的評價模型.

建立有關路線定價的數學模型，探索出關于路線任務的總成本定價以及3次報價.給出調價策略，評價對線路任務所給出的定價.要給出定價需要對前期的數據進行擬合分析，得到定價與指標之間的相關性，基于擬合模型對數據指標進行擬合預測從而得到所需的3次報價及總成本.最終可以根據得到報價后的調價系數來給出調價策略，促進快速成交和降低承運成本.

1 定價因素的研究

1.1 數據的預處理

由于數據量非常龐大，為使得建立的模型更加準確的得出路線價格，需要對數據進行分析并通過相應的方法對其進行數據的預處理，這有利于后續模型的建立與求解.

通過對數據體的分析，將變量分為3類：文本說明變量，定量描述變量，事件類型變量.其中文本說明變量主要指數據的基本特征和完整情況，如任務ID、始發時間、出發省份等.定量描述變量主要描述數據的真實值，如路線價格、調價比例等.事件類型變量描述數據的類別，如業務類型、需求類型、是否續簽等.

為更好的找出影響無車承運人平臺進行貨運線路定價的主要因素，首先對與定價無較強相關性的因素進行刪除

在得到較為相關的變量之后對這些變量的含缺失值樣本進行刪除，從而得到預處理后的數據樣本.

1.2 確定影響定價的主要因素

在結束數據的預處理之后需要對影響定價的主要因素進行篩選，對于數據進行降維的算法有很多，但因為變量中含有轉為虛擬變量的事件類型變量，所以不能使用主成分分析、因子分析等來對定量變量進行降維算法處理，故選擇逐步回歸法對所有變量進行降維，并且主要考慮事件類型變量的選擇，再用R聚類對定量變量進行降維，同時也可以驗證定量變量選擇的準確性.

1.2.1 逐步回歸算法

逐步回歸模型有3種操作方法[4].

1) 向前選擇 首先模型中只有一個單獨解釋因變量變異最大的自變量，之后嘗試將加入另一自變量，加入后整個模型所能解釋的因變量變異是否顯著增加這一過程反復迭代，最終達到沒有其他自變量還能符合加入模型的條件.

2) 向后消除 把所有變量全部放入模型中，再把其中一個自變量剔除，由此來探尋整個模型解釋因變量的變異是否產生了顯著的變化，然后將其中解釋量減少得最少的變量進行剔除；再由此過程進行不斷迭代，一直要等到沒有多余自變量再能符合剔除的條件即可.

3) 雙向消除 對整個模型中的所有變量進行檢驗，剔除作用不顯著的變量.目的在于盡量能夠得到一個最優方案的變量組合結果.

再進行回歸前對選擇的變量進行描述性的統計，計算得到各變量之間的相關系數.斯皮爾曼相關系數并沒有皮爾遜相關系數高，但皮爾遜系數要求數據的連續、正態性和線性相關性.為此本文還選取變量繪制了正態分布Q-Q圖，如圖1和圖2所示.

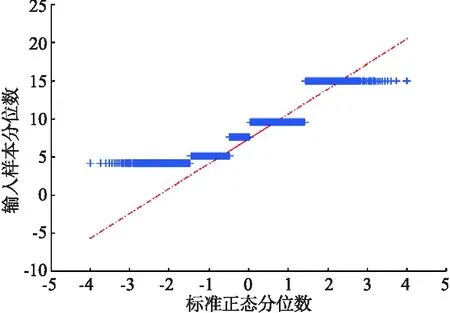
圖1 車輛長度與正態分布的Q-Q圖

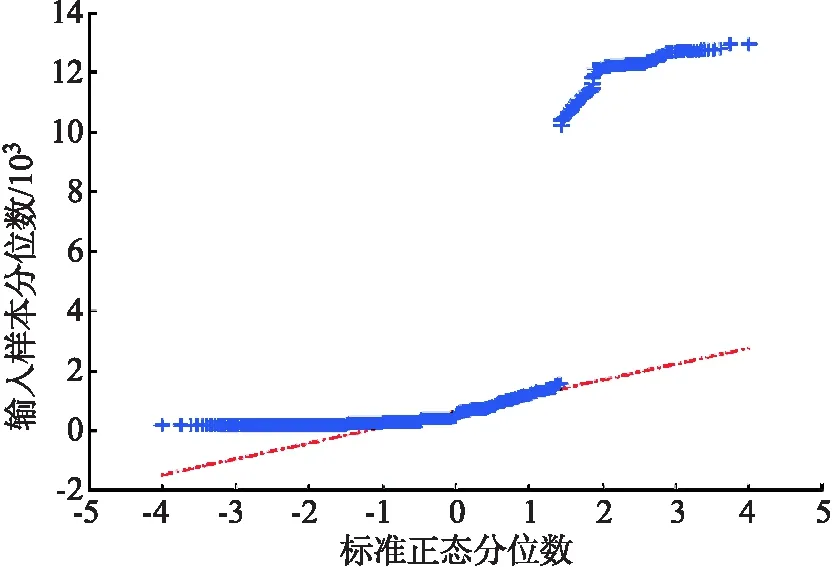
圖2 線路總成本與正態分布的Q-Q圖

由2幅Q-Q圖上所描繪點并不近似于一條直線可以看出，存在變量不服從正態分布的問題.所以這里選擇使用斯皮爾曼相關系數.

文中選用向前選擇算法[5]剔除冗余變量后得到的32個剩余變量來建立模型并進行求解，得到顯著性變量18個，模型匯總表和模型評價表如表1和表2所示.

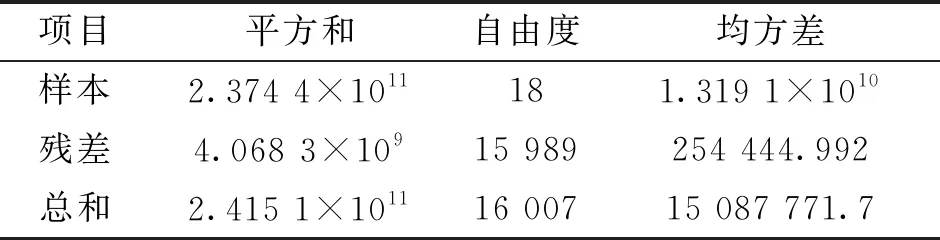
表1 模型匯總

表2 模型評價

為檢驗剔除過后的變量是否還存在多重共線性的問題，對變量的膨脹因子進行求解得到Mean VIF>10 說明存在多重共線性問題，評價可能失真，此時需要對變量進行進一步的篩選.采用Rlasso算法來對變量進行篩選，Rlasso是一種嚴格的懲罰方法，它可以控制過度擬合.最終得到相關變量及系數如表3所示.

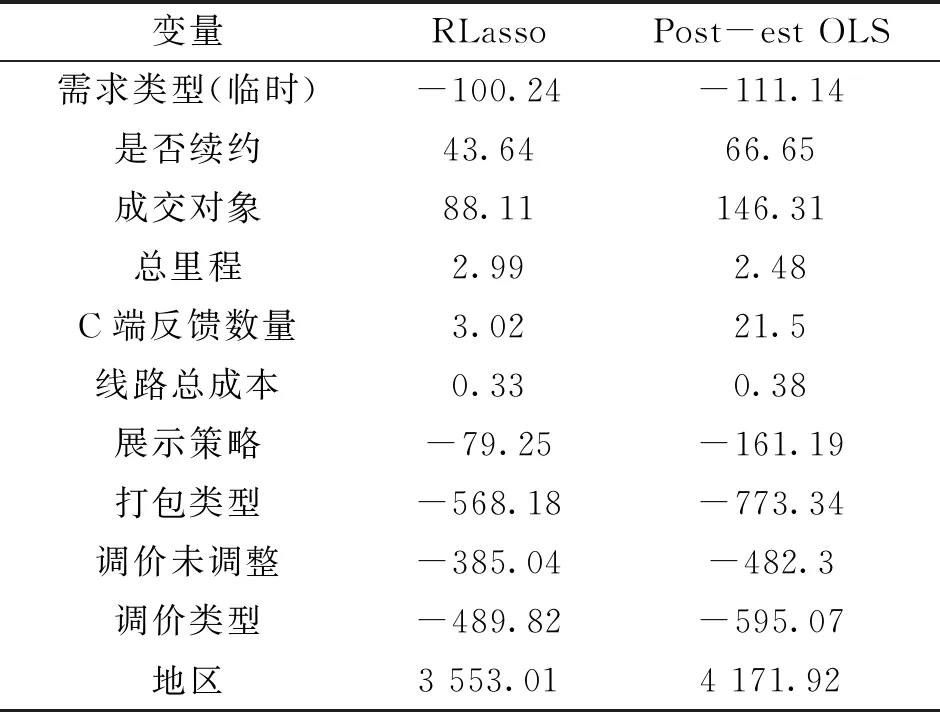
表3 最終變量

1.2.2 R型聚類算法及求解

R型聚類是一種聚類方法，一般用于對指標進行降維處理[6].通過編程建立模型[7]并將定量描述變量代入運行得到聚類樹狀圖，如圖3所示.

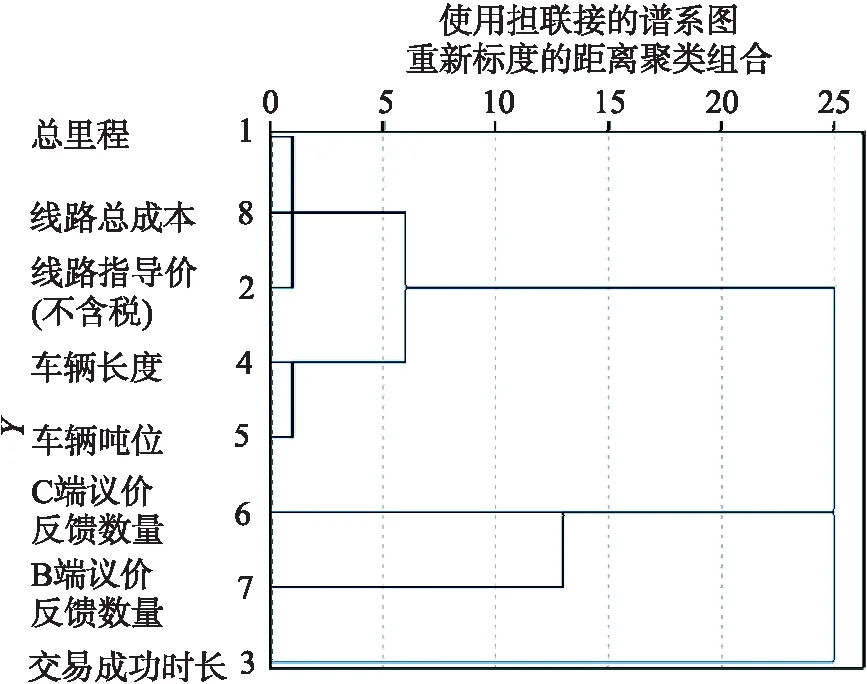
圖3 聚類樹狀圖

從圖3可以看出指標總里程、線路總成本、線路指導價(總成本)具有較大的相關性，最先被聚類到一起.將指標分為4類，每一類指標以及最終確定的4個代表性指標如表4所示.

表4 各類別指標基本信息

從以上結果可得出，交易成功時長與其他指標存在區別，各為一類，其他類中各指標均有明顯相關的聯系.一般來說這幾類數據都與最終的線路定價有相關性，這也說明本模型對于該問題具有較好的適應性.

2 基于專家打分-Topsis評價模型

要對已成交的貨運線路歷史交易數據中的定價進行評價，首先要選擇合適的評價指標.因無車承運人在當前階段較為關注的問題是如何快速成交并降低承運成本，結合表4中的代表性指標，如線路指導價、線路價格、交易成功時長、線路總成本等因素，對已經成交貨運線路歷史交易數據中的定價來進行評價.

專家打分法是一種定性描述定量化方法，它首先根據評價對象的具體要求選定若干個評價項目，在根據評價對象的具體要求選定若干評價指標[8].根據指標定出標準，聘請若干專家憑借自己的經驗按此評價標準來給出各個項目的評價分值，并對其進行集結[9].其公式為：

(1)

其中W代表評價對象的總分值；n代表指標項數；wi代表第I項指標得分值.

1) 經專家打分法得到的各項權指標權重如表5所示.

表5 指標權重

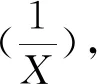
3) 數據歸一化處理，為了消除不同量綱對評價結果的影響，使用評價指標在同一個量綱體系下進行比較，需要對原始數據進行歸一化處理.處理方法為：

i=1,2,…，160 008,j=1,2,3,4.

(2)

4) 確定最劣向量Z-和最優向量Z+，其中Z-為同一指標的最小歸一化值，而為Z+同一評價指標的最大歸一化值.

5) 計算各樣本與理想解的加權歐式距離[10]及各歷史訂單與理想解之間的相對接近程度

(3)

(4)

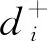
6) 對得到的結果進行排序，得到專家打分—Topsis模型計算的點單ID得分排序.

3 定價預測模型

要給出所得數據的3次報價及總成本的定價，其實也就是結合前期求得數據中指標與定價之間的相關聯系，將相關指標通過這種相關聯系映射成3次的定價.為了方便之后對建立的模型進行評價，故選擇線路成本、線路指導價、線路價格、交易時長為輸出變量.

3.1 Levenberg-Marquardt-BP及求解

BP是一種為減小誤差使網絡的誤差平方和最小而通過梯度下降的學習方式反向傳播來不斷調整網絡的權值和閾值從而達到目標參數的多隱含層層前饋網絡[11].高斯-牛頓法為避免發散可以調節下降步伐和方向[12].當發現網絡訓練梯度下降過快的時候，應當合理采用偏小的下降系數，從而使其更相似于高斯牛頓法，反之，當發現網絡訓練梯度下降過慢時，應選用偏大下降系數，使其更相似于梯度下降法.

通過Matlab神經網絡工具箱設置參數并訓練輸出得到結果，其學習誤差在迭代數64處達到最小.模型總擬合度達到 0.994 52，如圖4和圖5所示.

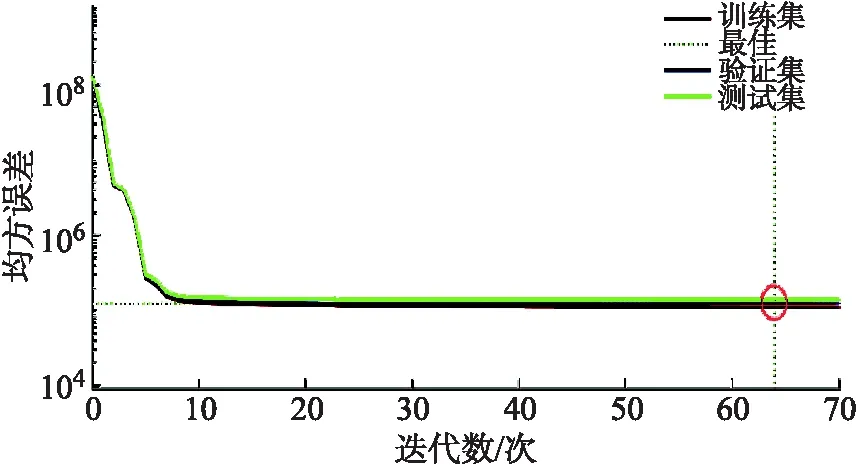
圖4 學習誤差下降曲線

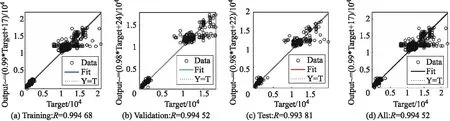
圖5 模型擬合度檢驗

3.2 Bayesian Regularization-BP及求解

貝葉斯決策理論是主觀貝葉斯派歸納理論的重要組成部分.貝葉斯決策就是在不完全情報下，對部分未知的狀態用主觀概率估計，然后用貝葉斯公式對發生概率進行修正，最后再利用期望值和修正概率做出最優決策[13].該算法通常需要更多時間，但是對于困難，較小或嘈雜的數據集，可以得到很好的概括.訓練根據自適應減重(正則化)停止.

通過Matlab神經網絡工具箱設置參數并訓練輸出得到結果，其學習誤差在迭代數216時達到最小，模型總擬合度達到 0.994 82，如圖6和圖7所示.

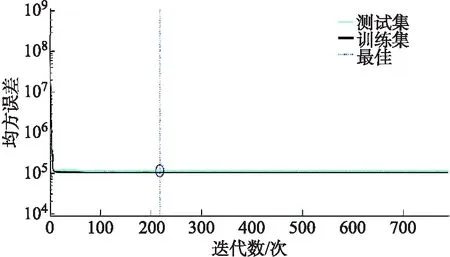
圖6 學習誤差下降曲線

圖7 模型擬合度檢驗

3.3 Scaled Conjugate Gradient-BP及求解

共軛梯度法能夠有效改善前饋神經網絡的明顯缺陷，例如局部震蕩和收斂速度低.采用共軛梯度法會在共軛梯度方向進行修正權值的操作，并采用概率接受原則來對是否需要進行目標函數變化進行判斷，共軛梯度法具有較快的全局收斂性[14].此算法需要較少的內存.當通用性停止改善時，訓練會自動停止，驗證樣本的均方誤差增加.

通過Matlab神經網絡工具箱設置參數并訓練輸出得到結果，其學習誤差在迭代數158時達到最小，模型總擬合度達到 0.993 55，如圖8、圖9所示.

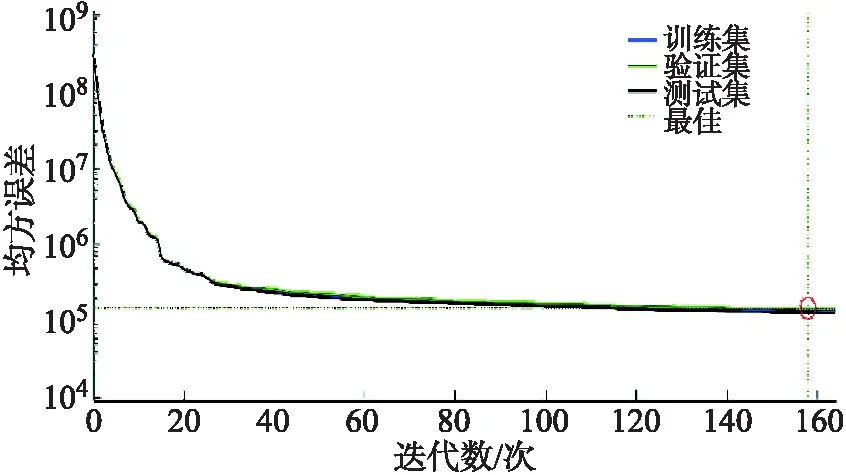
圖8 學習誤差下降曲線

3.4 最優預測模型的選取及求解

為選取最優的預測模型，需要對上述3個模型的運行結果進行對比評價，如表6所示.

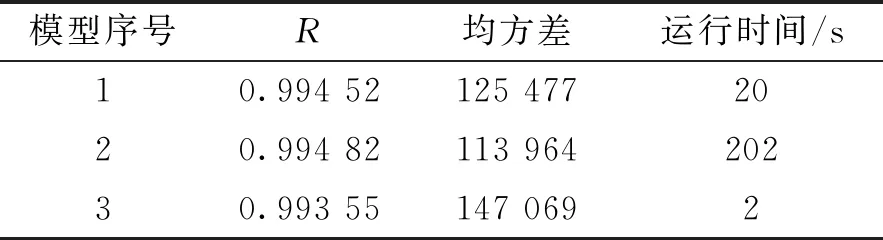
表6 模型評價

綜合3個指標來看Levenberg-Marquardt是最優的模型，故使用它來對評價模型中的指導路線價格、路線價格、總成本以及交易時間來進行預測.其中指導價格對應第一次報價，路線價格對應第三次報價.由于前期數據未求出第二次報價，所以本文采用線性插值的方法來對第二次報價進行求解，調價策略由計算調價比例得到.

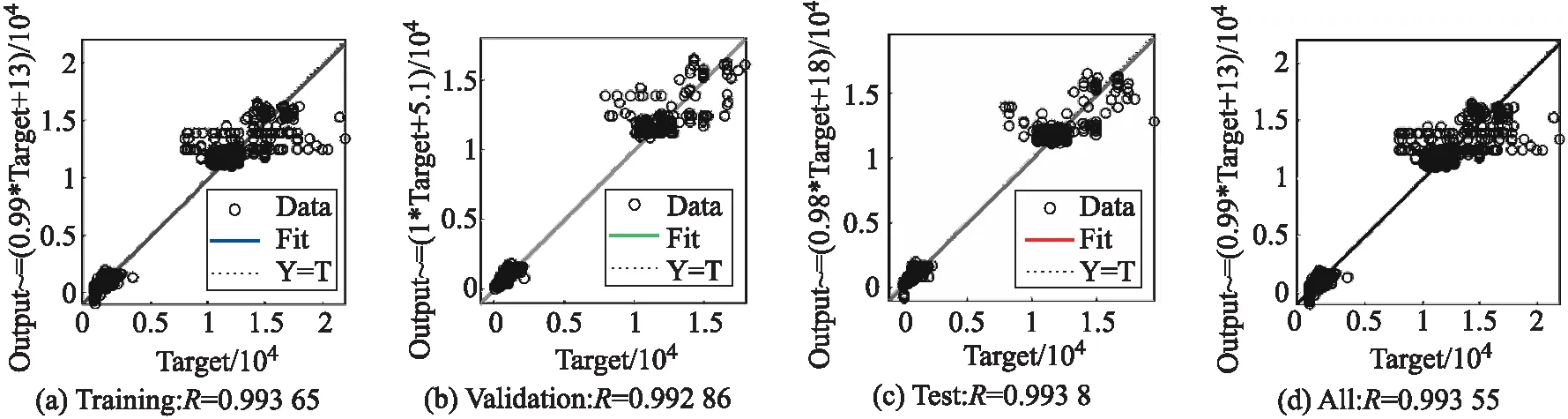
圖9 模型擬合度檢驗

4 結語

隨著我國無車承運行業的快速發展，各類商業模式迎來了百花齊放的時段.預計到達2020年年初的時候，在200多家的無車承運人試點當中，將會有45.6%是屬于合同物流的業務，而大約66.4%將會從事與普貨運輸相關的領域，另外，其中的47.7%左右會選擇從事傳統物流與互聯網轉型這樣的綜合業務，除此之外還有47%是有關于互聯網加物流的另一種綜合業務，這類平臺在貨運行業的集約化程度已經可以看做十分健全有力了，在未來將整合社會零散運力大約135.1萬輛，高效提升相關行業的集約程度，提高運轉效率，但與之密切相關的承運線路科學合理定價問題卻是大多數無車承運人平臺急迫需要解決的.團隊一直密切關注無車承運人平臺科學定價問題，進行了積極研究，并依據文中所述的研究方法與結論，對無車承運人平臺的科學定價提出以下看法與建議：

從所得出的相關系數表中可以看出，線路總成本是線路定價和線路指導價的最主要影響變量之一，其間滿足強烈的正相關；而線路總成本又與總里程、車輛長度、車輛噸位有強烈的正相關關系；與運輸等級與運輸地區也有一定的相關關系.所以總里程較大、車輛長度與噸位較大時，線路的總成本就會較大，所以定價應該相對較高.

將已成交貨運線路歷史交易中的定價數據進行TOPSIS法建立了評價模型，并證實了基于TOPSIS評價模型而得到的評價效果能夠適用于該平臺的評價體系.

關于線路定價的數學模型，利用3種算法建立不同的BP神經網絡模型，并利用現有的數據對3種模型的擬合效果做了對比，在考慮時間和擬合精度的情況下得到了最優的Levenberg-Marquardt-BP做為預測模型，為無車承運人平臺的定價問題提供了參考.