光譜差分策略在擴散近似模型和簡化球諧近似模型中的應用

劉艷秋，胡先功，張 衡，郭紅波，賀小偉，3*

（1.西北大學 信息科學與技術學院，陜西 西安 710127；2.西北大學 西安市影像組學與智能感知重點實驗室，陜西 西安 710127；3.西北大學 網絡和數據中心，陜西 西安 710127）

1 引 言

生物發光成像（Bioluminescence Imaging，BLI）是一種非侵入性、非電離的分子成像技術，能夠在活體中顯示熒光素標記的腫瘤細胞。由于腫瘤細胞具有較高的敏感性和特異性，BLI在小動物的預臨床研究中發揮著越來越重要的作用[1-3］。與BLI相比，生物發光斷層成像（Bioluminescence Tomography，BLT）是采用生物發光源三維重建，能更準確地定位和量化腫瘤信息[4］，已廣泛應用于預臨床研究。然而在實際生物應用中，由于光子在生物組織中的復雜傳播和探測到的表面光子的限制，BLT的病態性限制了其光源重建精度[5-6］。

在生物發光成像中，光從生物體內部光源發出，通過復雜生物組織結構到達生物體表面。描述光在生物體內的傳輸過程的一個標準模型為輻射傳輸方程（Radiative Transfer Equation，RTE）[7］。然而，在實際的生物發光成像中，RTE的計算成本很高[8］。最典型的方法是使用RTE的擴散近似方程（Diffusion approximation Equation，DE）作為前向模型。DE基本上是RTE的一階球諧波近似的特例，是描述光在組織中傳播速度最快的模型，但其精度有限，特別是在低散射區域、高吸收區域和邊界處[9］。為了克服DE模型的局限性，需要對RTE進行高階近似。相比于其它的高階近似模型（如SN、PN模型），簡化球諧近似（Simplified spherical harmonic approximation，SPN）的計算負載更低，三階簡化球諧近似（3rd Simplified spherical harmonic approximation equation，SP3）已被廣泛應用于生物發光成像[10-12］。但由于SP3也是對RTE的近似，模型誤差仍然存在，而且高階近似需要求解的未知量是DE的幾倍，帶來了更高的計算負載。混合SP3和DE光傳輸模型（Hybrid Simplified spherical harmonics with Diffusion Equation，HSDE）的提出，一定程度上平衡了光傳輸精度和速度[13-14］，然而簡化模型對于RTE的近似誤差仍然存在，SP3模型導致的計算負載也不能完全得到緩解。

另外，由于將成像物體表面檢測到的二維發光能量轉化為物體內重建的三維生物發光源的BLT逆問題是一個數學不適定問題[4］。因此，需要融合足夠的先驗知識來保證解的唯一性和穩定性。可行域策略和多光譜方法分別通過減少未知變量和增加已知數據量減少光源重建的病態性，是BLT重建中常用的兩種策略[15］。此外，基于壓縮感知（Compressed Sensing，CS）理論的各種稀疏算法，如采用稀疏正則化項[16-17］（如L0和L1），使用貪婪策略[18］或采用稀疏貝葉斯方法[5，19］等算法，用來減少噪聲對重建結果的影響，使光學分子斷層成像的重建精度不斷提高。

在我們之前的研究中，分析了RTE的擴散近似產生的光傳輸誤差、數據采集過程中成像系統存在的噪聲以及逆問題固有的病態性對BLT光源重建精度的影響，提出了光譜差分策略，減弱DE光傳輸模型和成像系統的系統誤差，并緩解重建問題的病態性[20］。在此基礎上，本文將光譜差分策略分別應用到DE和SP3光傳輸模型，首先對這兩種RTE近似產生的誤差進行分析，對比光譜差分策略對兩種光傳輸誤差的衰減作用，進而將光譜差分策略分別應用到DE和SP3光傳輸模型進行光源重建，旨在有效提高光源重建的準確性和效率。

2 理論方法

2.1 光傳輸過程及誤差分析

穩態的RTE為：

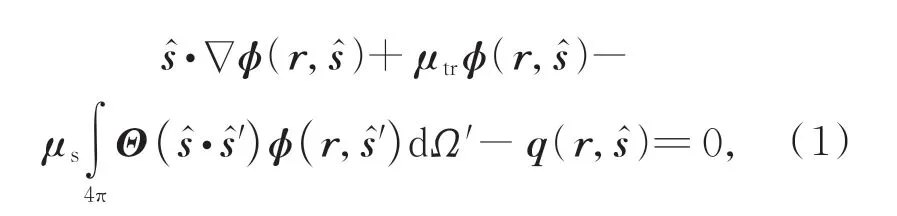
（1）DE光傳輸模型誤差

穩態擴散方程表示為：

通過有限元近似表示為：

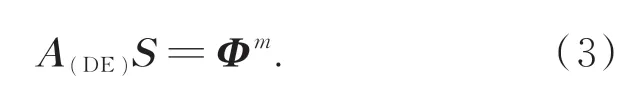
A(DE)為DE近似構造的系統矩陣，S為光源能量密度，Φm為表面節點上的光通量。

DE是RTE的一階球諧展開近似，在我們之前的研究中，分析了該近似過程對給定波長λ對應的系統矩陣A(DE)λ產生的誤差[20］，現將其簡單表示為：

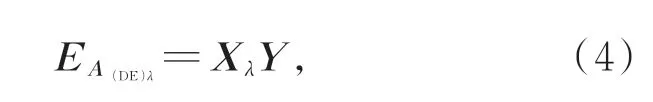
其中：受波長λ影響的量用Xλ表示，其它與波長無關的量用Y表示。

對于兩個波長λj和λk對應的誤差做差：

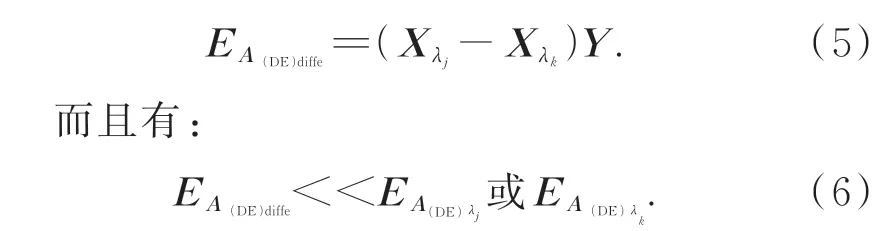
（2）SP3光傳輸模型誤差

高階簡化球諧近似方程可以表示為：

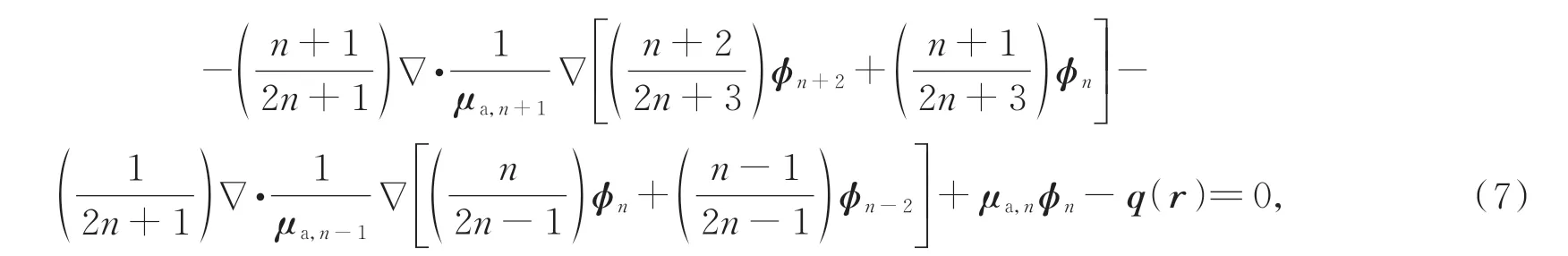
其中：μa，n=μa+μs(1-gn)，g為各向異性參數，n為階數；φ為勒讓德多項式。N=3時，SP3模型的方程為：

φi是輻射度的勒讓德矩φi的線性組合。通過有限元近似表示為：

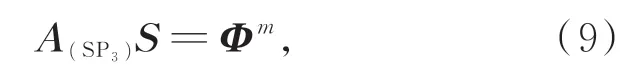
其中，A(SP3)為SP3近似構造的系統矩陣，類似于DE近似。SP3近似對給定波長λ對應的系統矩陣A(SP3)λ產生的誤差可以表示為：

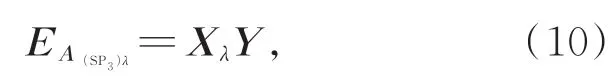
其中：受波長λ影響的量用Xλ表示，其它與波長無關的量用Y表示。

對于兩個波長λj和λk之間的差值：

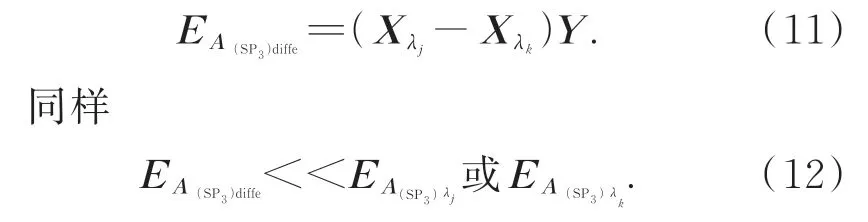
表明對于DE和SP3光傳輸模型，由于波長接近的光在通過相同光學路徑時遇到相近的系統響應，對相近波長的測量數據做差可以一定程度上消除光傳輸模型產生的誤差。

2.2 光譜差分策略在光源重建中的應用

由于成像問題的非唯一性以及光源重建的病態性，已證實多光譜方法可以緩解其病態性[21，22］。假設測量數據 包含3組波長，對于DE和SP3光傳輸模型，將各自系統矩陣組合：

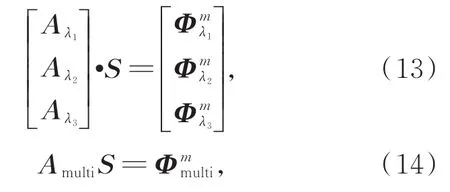
其中：Aλi是給定波長λi對應的系統矩陣，Φmλi是 相同波長的表面光能量，Amulti和Φmmulti是組合的系統矩陣和表面光能量。

在多光譜方法的基礎上，光譜差分策略利用每個測量波長之間的數據差，將式（13）和（14）變換為：

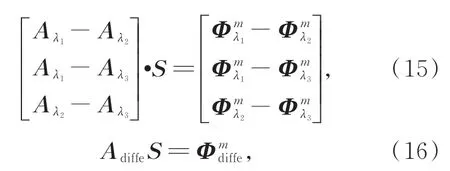
其中，Adiffe和Φmdiffe分別為差分的系統矩陣和差分的表面光能量。

由于光源在生物體中通常是稀疏分布的，且表面測量數據嚴重不足，基于壓縮感知理論，采用Lp正則化方法將式（16）的重建模型轉化為以下最小化問題：

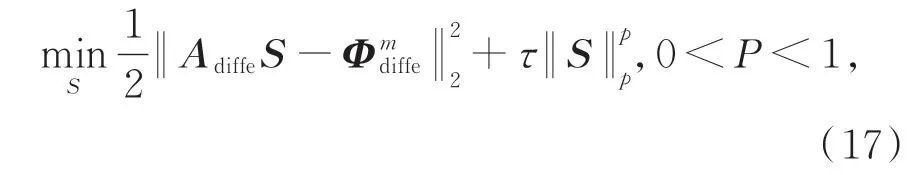
3 實驗與結果分析

3.1 實驗設置

采用數值仿真實驗驗證光譜差分對于DE和SP3光傳輸模型誤差的緩解作用，以及光譜差分策略在BLT光源重建中的性能。前向仿真實驗和光源重建實驗均采用常用的數字鼠模型，只研究數字鼠的軀干部分，高度為35 mm，包括肌肉、心臟、胃、肝臟、腎臟和肺六個主要組織，如圖1（a）所示。在肝臟中設置一個半徑為1 mm的球形光源，其中心點坐標為（18 mm，8 mm，14.8 mm），位置如圖1（b）。在前向仿真實驗中，三維數字鼠軀干離散網格如圖1（c）所示，包含20 263個節點。光源重建實驗網格如圖1（d）所示，包含10 139個節點。本文選用BLT中常用波段范圍的三個波長630 nm、650 nm和670 nm進行實驗，由文獻[25］中總結的公式，計算得到各生物組織在各個波長下對應的光學參數如表1所示。

在前向仿真實驗中，以蒙特卡羅方法（Monte Carlo extreme，MC）[26］獲得的表面光能量作為對比標準。以平均誤差（Average error）和余弦相似度（Cosine similarity）作為定量評價指標，分析DE和SP3引起的光傳輸模型誤差。

測量的表面光能量差值的計算方法如下：

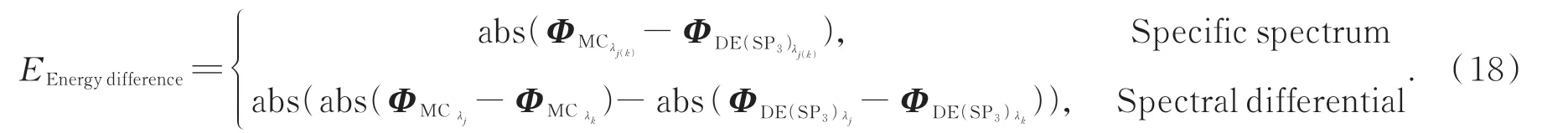
計算630 nm、650 nm和670 nm波長下，分別通過MC和DE（SP3）獲得的表面光能量的差異，以及MC和DE（SP3）獲得的不同波長的表面光能量任意兩組波長組合，差分之后的能量誤差。進而采用平均誤差定量評價上述能量誤差：

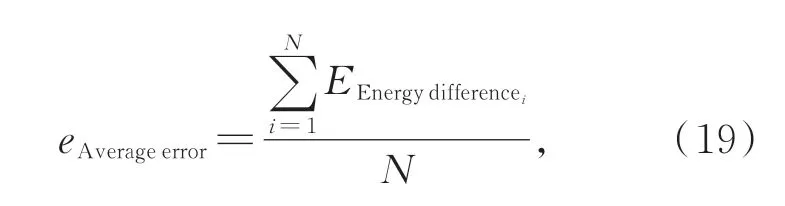
其中：EEnengydifferencei代表第i個表面節點對應的能量誤差，N為表面節點總數目。

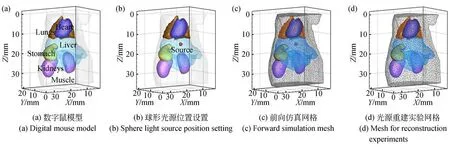
圖1 數值仿真實驗設置Fig.1 Numerical simulation experiment settings

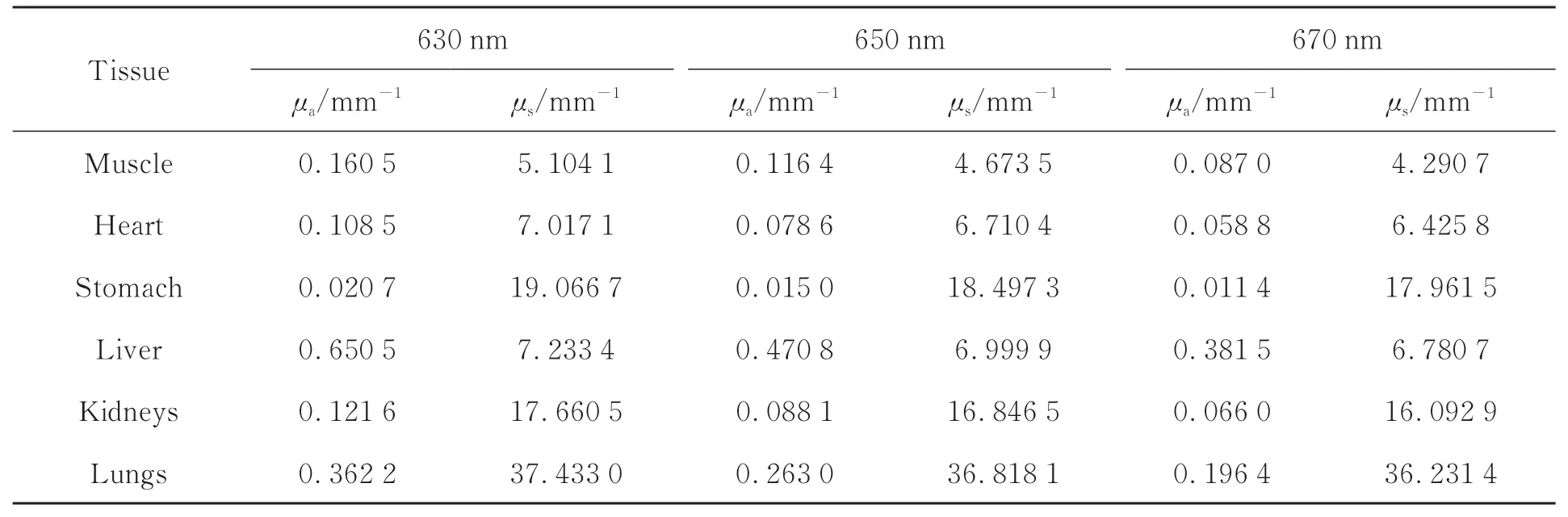
表1 不同波長下數字鼠組織的光學參數Tab.1 Optical parameters of the mouse tissues at different wavelengths.

同時采用余弦相似度評估表面光能量的差異以及差分數據的差異：

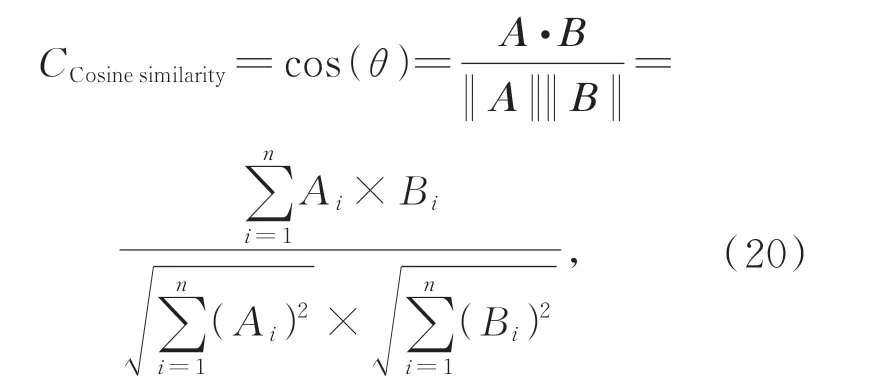
其中：Ai、Bi分別表示被比較的向量A、B的分量。其值越接近1，表明兩個向量越接近。

在光源重建實驗中，采用常用的定量分析指標：定 位 誤 差（Location Error，ILE）、Dice系 數（IDice）和對比噪聲比（Contrast-to-Noise Ratio，ICNR），定量分析各方法的目標定位、形狀恢復和圖像對比度性能。這些指標的計算方法如下：

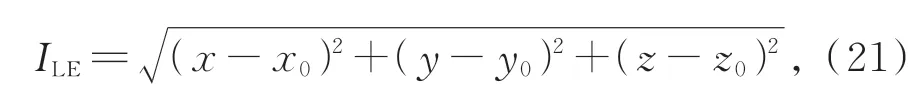
其中：ILE表示重建光源與真實光源之間的位置偏差，（x，y，z）和（x0，y0，z0）分別為重建能量加權中心點的坐標和真實光源中心的坐標。

Dice系數用來評價形狀恢復，其中，X、Y分別為重建光源區域和實際光源區域。

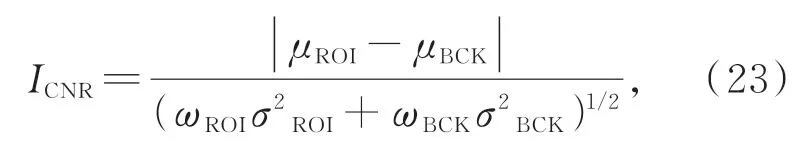
對比噪聲比用來評價圖像對比度，其中：下標ROI和BCK分別表示被成像物體的目標區域和背景區域，μ、ω、σ分別表示平均強度值、加權因子和方差。

3.2 前向仿真實驗結果

為了分析比較DE和SP3模型在光傳輸過程中產生的誤差，進行了前向仿真實驗，進而驗證光譜差分對于光傳輸誤差消除的有效性。

首先，采用MC方法獲得數字鼠模型對應630 nm、650 nm和670 nm波長的表面光能量，為了便于展示光能量的細節，將其投影到X-Z平面，如圖2（a）所示。相應的，分別采用DE和SP3模型獲得數字鼠模型在各波長的表面光能量，分別如圖2（b）、（c）所示。對于各個光傳輸模型獲得的表面光能量，都表現為波長越長，對應的表面光能量越強。這是因為在較長波長下，組織散射效應減弱，光穿透能力增強。對比圖2（a）、（b）和（c），直觀上，DE模型在630 nm獲得的表面光能量和MC與SP3差異較明顯，而在650 nm和670 nm對應的表面光能量較為接近。

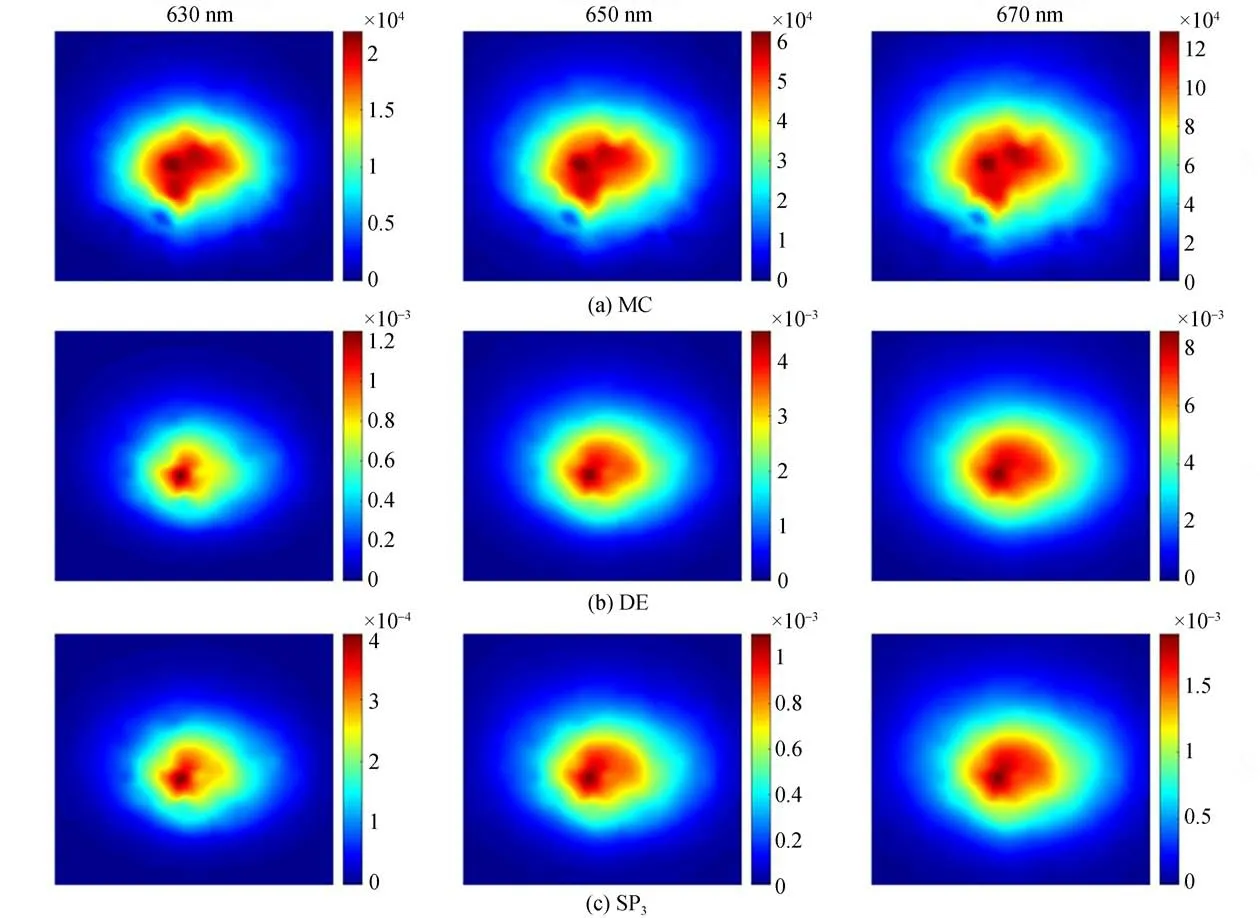
圖2 MC、DE和SP3模型獲得的表面光能量在X-Z平面投影Fig.2 X-Z plane projection of surface luminescence fluxes obtained by the MC，DE and SP3，respectively.

為了定量分析DE和SP3模型的光傳輸誤差，采用公式（18）計算各特定光譜MC和DE（SP3）獲得的表面光能量的誤差，再利用公式（19）計算平均誤差。進而應用光譜差分，任意兩組波長組合，利用式（18）計算各組測量波長之間的能量差異，獲得對應的差分后的能量誤差，再利用式（19）計算出平均誤差。DE和SP3模型以及光譜差分后DE和SP3對應的平均誤差值如圖3所示，對于DE模型，630 nm對應的能量平均誤差較大，650 nm、670 nm對應的能量誤差相應減小。SP3模型在各波長對應的能量平均誤差和DE模型呈現相同的變化趨勢，且各能量平均誤差值都相對DE模型減小，表明SP3模型比DE模型具有更高的傳輸精度。分別對DE模型和SP3模型獲得的表面光能量進行光譜差分，能量平均誤差相對減小，尤其對于630 nm對應的能量平均誤差改善較為明顯，而且應用光譜差分策略后SP3模型比DE模型獲得了更小的能量平均誤差。

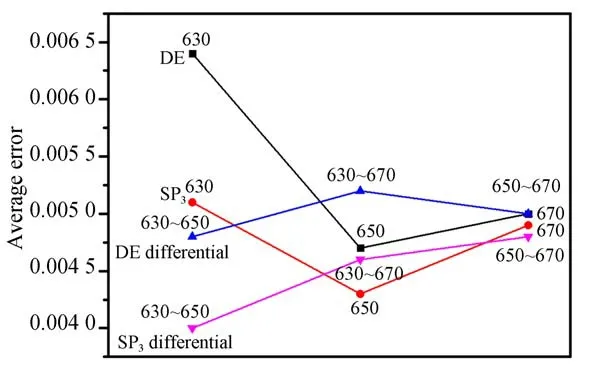
圖3 MC和DE（SP3）獲得的表面光能量的平均誤差，以及MC和DE（SP3）獲得的表面光能量通過光譜差分后的平均誤差Fig.3 Average errors of surface light energy obtained by MC and DE（SP3）and the average errors after applying the spectral differential

為了進一步驗證前向仿真實驗的結果，由公式（20）計算了MC和DE（SP3）在同一波長下獲得的表面光能量的余弦相似度，如圖4所示，余弦相似度越接近1，表明能量值越接近。由圖4可以看出，SP3模型的余弦相似度大于DE模型。進而通過MC與DE（SP3）獲得的各波長的能量差計算余弦相似度，從圖4可以看出，光譜差分后DE和SP3對應的余弦相似度顯著增加。計算各個特定光譜和光譜差分對應的余弦相似度的平均值和方差，DE和SP3模型對應的三組波長余弦相似度的平均值和方差分別為0.985 8±0.006 0和0.988 1±0.003 0，任意兩組波長組合光譜差分后DE和SP3模型對應的余弦相似度的平均值和方差分別為0.989 3±6.127 6e-04和0.990 8±1.042 7e-04。表明光譜差分能夠有效減小DE模型的傳輸誤差，使其接近SP3模型的傳輸精度，并且對SP3模型應用光譜差分能夠獲得更高的傳輸精度。

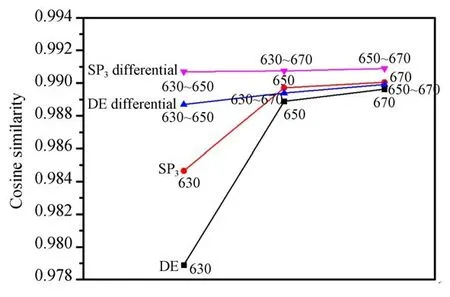
圖4 MC和DE（SP3）獲得的表面光能量的余弦相似度，以及通過MC與DE（SP3）獲得的各波長的能量差計算的余弦相似度Fig.4 Cosine similarity of surface light energy obtained by MC and DE（SP3）and the cosine similarity calculated by the difference of energy between each measured wavelength obtained by MC and DE（SP3）

進而對各方法的運算效率進行論證，在獲得各波長DE和SP3模型對應的表面光能量的同時記錄下了其所耗時間，DE模型在630 nm、650 nm和670 nm波長下耗時分別為：212.90 s、208.41 s和211.73 s，而SP3模型在三個波長耗時分別為：992.55 s、990.35s和994.26 s，DE模型耗時遠低于SP3。對三組波長對應的表面光能量進行光譜差分，DE模型的光能量差分總耗時為0.031 s，SP3模型的光能量差分總耗時為0.030 s。即采用DE模型獲得三組波長的光能量并進行光譜差分，總耗時仍低于SP3模型獲得一組波長光能量的耗時。

3.3 光源重建實驗結果

為了驗證光譜差分策略在光源重建中的可行性與適用性，進行逆向光源重建實驗。采用MC方法模擬 的630 nm、650 nm和670 nm波長的表面光能量作為測量的表面數據。分別對DE和SP3模型獲得的三組波長對應的系統矩陣進行光譜差分，獲得式（16）的表達，采用ISTA方法重建，并將MC獲得的630 nm波長的表面光能量分別采用DE和SP3模型進行光源重建作為對比。

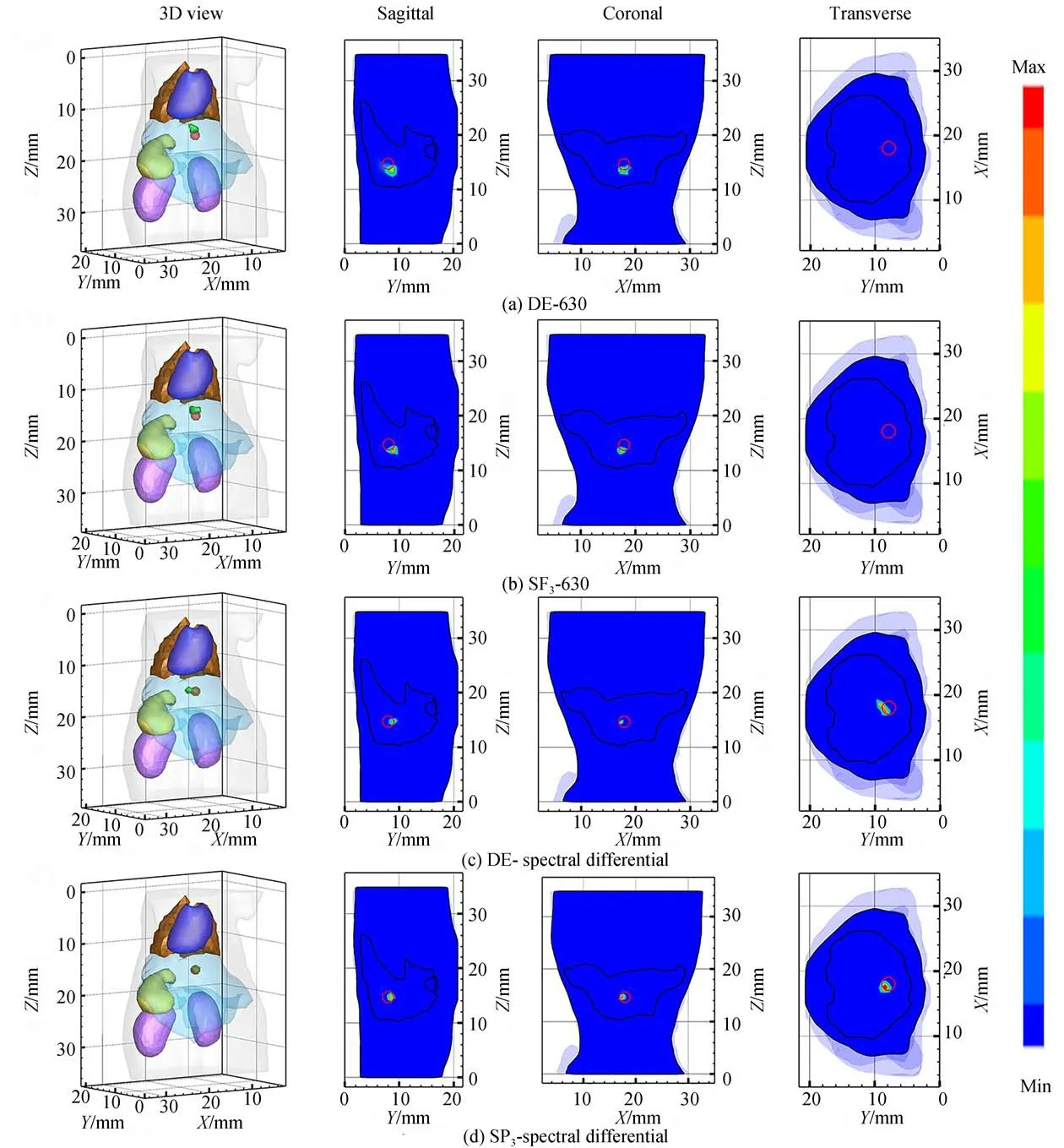
圖5 光源重建實驗結果Fig.5 Experimental results of source reconstruction

DE和SP3模型在630 nm對應的重建結果分別如圖5（a）和（b）所示，采用光譜差分策略的DE（DE-spectral differential）、SP3方 法（SP3-spectral differential）對應的重建結果分別如圖5（c）和（d）所示。三維視圖中的紅色球體表示真實光源的實際位置，綠色不規則形狀為重建光源。相應的矢狀面、冠狀面和橫切面根據真實光源的中心位置來確定，截面圖中的紅色圓圈代表真實光源的位置。圖5（a）、（b）中重建光源距離真實光源有一定的偏離，且由于重建光源位置比真實光源偏上，在Z=14.8 mm橫切面圖中觀測不到重建光源信息。圖5（c）、（d）中DE-spectral differential和SP3-spectral differential方法都能夠較為準確地定位真實光源，然而，相比于DE-spectral differential方法，SP3-spectral differential方法 的重建 光源與真實光源重疊更好。

表2中的評價指標定量分析驗證了圖5中的結論，DE和SP3模型在630 nm對應的重建結果LE均大于1 mm，且Dice較小。這和前向仿真實驗中，在630 nm波長DE和SP3模型獲得的表面光能量和MC的誤差較明顯的結論一致。DEspectral differential方法獲得的LE小于1 mm，且Dice和CNR值相對增大，提高了光源重建的準確性。而SP3-spectral differential方法重建光源的LE最小（0.724 mm），Dice和CNR值最大，在目標定位、形狀恢復和圖像對比度等方面有更好的效果。這是由于光譜差分策略在光源重建過程中，有效減少了DE和SP3模型的光傳輸誤差，提高了模型精度，并且緩解了BLT逆問題的病態性，使光源重建的位置誤差小于1 mm，獲得了更準確的重建精度。

表2 光源重建實驗的定量結果Tab.2 Quantitative results in source reconstruction experiment

此 外，DE模型 獲 得630 nm、650 nm和670 nm波長對應的系統矩陣耗時分別為33.61 s、33.66 s和34.81 s，SP3模型獲得三組波長對應的系統矩陣耗時分別為：1 530.68 s、1 520.63 s和1 522.52 s，DE模型構建系統矩陣耗時遠低于SP3。對三組波長對應的系統矩陣以及表面光能量進行光譜差分，獲得式（16）中差分的系統矩陣和差分的表面光能量，DE模型差分總耗時為0.401 s，SP3模型差分總耗時為0.414 s。即采用DE模型獲得三組波長的系統矩陣，并對系統矩陣和表面光能量進行光譜差分，總耗時仍低于SP3模型獲得一組波長數據的耗時。

4 結 論

在BLT研究中，高階光傳輸模型可提高光在生物組織中的傳輸精度，多光譜方法可降低逆問題病態性，從不同角度提升光源信息的重建精度。在此基礎上，本文對DE和SP3光傳輸模型獲得的表面光能量進行光譜差分，對比了光譜差分策略對兩種光傳輸誤差的衰減作用，前向仿真實驗結果表明光譜差分策略能有效地減少DE和SP3的模型誤差，對DE模型采用光譜差分，能夠獲得接近SP3模型的傳輸精度，并且降低高階近似對運算時間和存儲空間的高要求。進而將光譜差分策略分別應用到DE和SP3光傳輸模型進行光源重建，實驗結果表明光譜差分策略在提高兩種光傳輸模型精度的同時，緩解了BLT中逆問題的病態性，使光源重建在目標定位、形狀恢復和圖像對比度等方面具有更準確的效果。其中DE模型結合光譜差分策略，在重建精度和速率上達到了較好的平衡。