船舶爬壁機器人電磁吸附設計分析

韓力春，王黎明，閆曉玲

(海軍工程大學 電氣學院控制工程教研室，武漢 430033)

船舶爬壁機器人與陸地機器人的不同之處在于其兼具移動和吸附功能，能夠于傾斜的船舶壁面上完成爬壁運動，通過配備除銹、清洗、焊接所需的高壓水槍、焊槍等裝置完成對應作業任務等，每種作業任務對吸附力的要求不同。此外，作業環境的船舶壁面并非平滑不變，往往存在水藻和鐵渣等障礙物的，這導致爬壁機器人與壁面的間距并非一成不變，對機器人的越障能力有一定要求。從移動方式來看，一般，履帶爬壁機器人比輪式的越障能力強；從吸附方式來看，多采用永磁吸附、負壓吸附和正壓吸附等。但這些吸附方式一般不可調節吸附力大小，難以使爬壁機器人應對存在障礙物的船舶壁面和不同的作業需求。為此，考慮采用電磁吸附爬壁機器人，設計新式電磁吸附裝置，對機器人進行力學分析，根據得到的最小吸附力條件設計電磁鐵結構。通過建立電磁鐵和永磁鐵有限元仿真模型，模擬船舶壁面與機器人的間距，驗證此電磁鐵的吸附能力，實現吸附力可調。

1 電磁吸附單元設計

1.1 爬壁機器人結構設計

結合船舶爬壁機器人作業環境，用SolidWorks三維設計軟件建立爬壁機器人整機結構見圖1。移動機構主要由履帶和帶輪等組成，吸附機構主要由滑軌和電磁鐵等組成，驅動機構主要由步進電機和行星減速器等組成，車體框架結構采用H形架構，電源、控制器、電機驅動模塊等安裝在車體框架上。電磁鐵等間距鑲嵌在履帶中，因此電磁鐵既是吸附機構，也是移動機構的一部分，機器人通過步進電機帶動帶輪和履帶使其移動于壁面之上，同時，通過與壁面接觸的部分電磁鐵產生吸附力吸附于壁面之上。

圖1 爬壁機器人整機結構圖

1.2 機器人最小磁力條件分析

運行于船舶，涉及到物體坐標系和慣性坐標系，需建立海面上的慣性坐標系-，以及船舶和爬壁機器人的物體坐標系-、′-′′′，如圖2所示，為船舶壁面傾角，范圍是0°～90°；為爬壁機器人姿態傾角，即機器人在′′軸與軸的夾角；平面為船舶壁面；′軸與平面的法向量方向一致。

圖2 坐標關系變換

結合文獻[12-13]和爬壁機器人在船舶壁面爬壁過程中的實際運行情況可知，臨界狀態主要包括沿船舶壁面下滑、平行于豎直方向的縱向傾覆、垂直于豎直方向的橫向傾覆、沿壁面法向方向掉落等幾種狀態，針對電磁鐵設計而言，需取臨界狀態中最小磁力條件中的最大者，即縱向傾覆力作為電磁鐵設計的最小磁力條件。

爬壁機器人會出現縱向傾覆是因為機器人本身的自身重力會產生傾覆力矩，力矩主要包括傾覆力矩與抗傾覆力矩，傾覆力矩會導致機器人傾覆，由重力分別在′′軸和′′軸上的分量乘以對應的力臂而來；抗傾覆力矩會阻止傾覆發生，由吸附力和摩擦力分別乘以對應的力臂而來。當傾角變化到一定程度，致使頂端電磁鐵與表面相接觸的B點處所受的支持力為零，B點處的摩擦力為0，進而傾覆力矩大于抗傾覆力矩，因為履帶為柔性體，所以由頂端電磁鐵開始，由B至A點的電磁鐵依次脫落，發生縱向傾覆，此時受力情況見圖3。

圖3 縱向傾覆力學分析

1)傾覆力矩。

(1)

2)抗傾覆力矩。

=·

(2)

3)縱向傾覆臨界條件。

≥

(3)

=2

(4)

式中:A、B點分別為機器人底端、頂端與壁面的接觸點；為機器人重心到船舶壁面的距離；為A、B 2點間距離；為單部電磁鐵的電磁力。

聯合式(1)～(4)得出：為使機器人不發生平行于豎直方向的縱向傾覆，單部電磁鐵的最小電磁吸附力所需要滿足的條件為

(5)

代入機器人參數，通過數值分析得到縱向傾覆力見圖4。由圖4可知，在=74°時取得極值，為178.19 N。

圖4 縱向傾覆力隨傾角的變化

1.3 電磁鐵設計

所選用的是直流吸盤式電磁鐵，電磁鐵為E型結構。經過經驗公式求此圓形電磁鐵線圈的匝數、線圈厚度、線圈高度，線圈厚度即為環形線圈的內外徑之差，線圈高度與厚度決定了電磁鐵外圍Q235鋼的半徑尺寸。

為保證安全吸附以及計算方便，要對最小吸附力留有一定裕度空間，將其值取為180 N。最終得到電磁鐵的結構設計參數為電磁鐵環形線圈內、外徑為30、10 mm，電磁鐵高22 mm，通過SolidWorks軟件設計的電磁鐵三維模型見圖5。

圖5 電磁鐵三維模型

2 電磁場數學模型分析

電磁鐵的場模型涉及到電場與磁場兩部分，其磁感線要穿過電磁鐵、空氣、船舶壁面等最少三種介質，一般用Maxwell方程組進行描述場模型，采用基于Maxwell方程組原理的COMSOL軟件的電磁學模塊進行仿真分析，然后用應力張量法推算出電磁力公式。Maxwell方程組的積分形式為

(6)

式中：為電場強度；為磁感應強度(T)；為電位移矢量；為磁場強度,A/m；為電磁鐵與空氣的閉合面。

此方程組從上至下依次對應靜電場的高斯定理、磁通連續性定理、法拉第電磁感應定律、安培定律，對應的原理圖見圖6。

圖6 Maxwell方程組原理示意

在均勻各向同性介質中，本構關系如下。

(7)

式中：ε為媒質的介質常數；μ為媒質的磁導率；σ為媒質的電導率；為電流密度，A/m。

在非均勻介質中，還要考慮電磁場量在界面上的邊值關系。為使磁場計算簡單，引入磁標勢的關系式為

(8)

根據式(7)的本構關系，考慮其中磁場與剩余磁通密度之間的本構關系，將約掉，即

=+

(9)

聯合式(6)、(8)、(9)，推導出磁標勢為

(10)

、、為已知，因此可通過式(10)和邊界條件求解，那么再聯合(8)、(9)就可以求出，為了達到更好的仿真效果，在有限元分析時，有限元模型邊界的尺寸將大于電磁鐵模型。

根據Maxwell應力張量法，得到電磁力 (即電磁場的應力)的定義式為

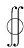
(11)

式中：為電磁張力應量。

(12)

式中：為單位張量；為真空介電常數；、為、與其自身的并矢張量。

聯合式(11) 、(12)得到電磁力為

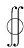
(13)

3 有限元分析

COMSOL軟件電磁學模塊的分析基礎是Maxwell方程組，COMSOL軟件內置Maxwell方程組的形式為亥姆霍茲方程，其是一定頻率下電磁波的基本方程，其解()代表電磁波場強在空間中的分布，每一種可能的形式稱為一種波模。

其穩態時，方程為

(14)

瞬態分析時，方程為

(15)

式中：為相對介電常數，是復數，可用虛部代表介質損耗；為磁矢量勢；為角頻率。

針對永磁鐵和電磁鐵這兩種不同的模型，分析中采用對應的物理接口，相應的控制方程采用對應的數學方程描述，簡化模型,去掉不必要的約束變量，用邊界條件方程來約束。

3.1 永磁體有限元仿真分析

永磁鐵仿真時，模型中無電流，只考慮磁場作用，此時磁通量守恒為其控制方程依據，磁絕緣(即磁場線與邊界平行)為其邊界條件，分別為

1)控制方程。

(16)

2)邊界條件。

·=0

(17)

式中：為磁體的法向量，乘積為零說明磁場線垂直于此法向量。

根據此前最小電磁力分析得到的磁鐵尺寸，建立永磁體有限元分析模型并導入，采用“磁場，無電流”這一物理場模塊，導入后永磁鐵和鐵板對象名稱為imp1。加入立方體空氣ext1將永磁鐵和鐵板完全包圍，通過布爾操作ext1+(imp1×ext1)使空氣充滿此立方體。并加載上述的控制方程和邊界條件，永磁鐵與壁面的間距為1 mm，船舶壁面采用100 mm×80 mm×20 mm的鐵板代替，得到的磁通密度仿真剖圖見圖7a)，永磁鐵與壁面接觸的磁通分布見圖7b)。

圖7 永磁鐵磁場有限元仿真模型

由圖7可見，磁感線在磁鐵內部是由S到N，外部則相反，符合實際磁感線方向，仿真正確，鐵板距離永磁鐵越近，系統密度越大、越密集，代表電磁力越大，此仿真下由COMSOL Multiphysics軟件計算出的最大磁力大小為160.783 N，在鐵板尺寸不變的情況下，以同樣的網格密度劃分、同樣的空氣空間，改變永磁鐵與鐵板間距離，以1 mm距離的等差梯度為自變量，進行1～10 mm間距的仿真，觀察磁力的變化情況，為使磁力變化趨勢更能貼合數據的變化走向，用MATLAB對所得數據進行擬合，見圖8。

圖8 永磁鐵的磁力與間距關系的變化

由圖8可見，磁力值隨著永磁鐵與壁面之間的間距的增大而變小，符合常識。間距在3 mm之前變化時電磁力減少幅度較大，磁力迅速減小，超過3 mm后電磁力變化幅度緩慢，但已經不滿足最小吸附力條件。爬壁機器人行走于船舶壁面上時，難免會遇到凸起的鐵銹和海藻等障礙，這時部分磁鐵與船舶壁面之間就不再是貼合狀態，而是短時出現上面曲線中不同的間距狀態，那么在傾角不變的情況下機器人所需要的最小吸附力沒變；但由于間距的改變而導致永磁鐵提供的吸附力變小，不滿足安全吸附條件，可是磁力又不可調，為此，引入電磁吸附以彌補磁力不可調的缺陷。

3.2 電磁體有限元仿真分析

電磁鐵仿真時，根據其電磁鐵吸附原理可知，仿真模型中通有電流，不僅要考慮磁場影響，還要考慮電場作用，此時控制方程依據內要加入安培定律，其邊界條件改為考慮磁矢量勢。

1)控制方程。

(18)

2)邊界條件。

×=0

(19)

電磁鐵是由線圈組成，線圈必須是閉合回路，4種不同類型的線圈見圖9，各線圈特性如下。

圖9 線圈類別

1)圖中的實體線圈未作任何近似處理，更能準確反映真實情況，但是在進行仿真運算時候要考慮很多的線圈的匝間影響，運算效率低。

2)邊界線圈特征近似描述不考慮厚度影響情況，以簡化網絡，不考慮上下方向的變化。

3)均勻化線圈是忽略匝間的相關影響的近似描述，忽略線圈電容近鄰諧振效應。因為電磁鐵所通的電流頻率很低，屬于低頻電磁場，線圈的趨膚深度小，可以忽略，不影響電感分析。只看磁場和電磁力方面，并不影響電磁鐵的仿真結果。

4)邊線圈常用于激勵場，查看磁通量大小，間接計算電感，但不能計算電阻和電容。

仿真模型采用均勻化線圈，用SolidWorks建立電磁體有限元分析模型，SolidWorks和COMSOL Multiphysics有聯合接口——LiveLink for SOLIDWORKS，模型的變動可實時同步到COMSOL軟件中。對于電磁鐵有限元分析，要加入的物理場模塊如下。

1)電路。所設計的電磁鐵采用直流24 V電壓源供電，此電路模塊即用于模擬電源供電。

2)磁場和電場。產生磁場和電場，仿真中控制方程和邊界條件的來源。

電磁體有限元分析得到的磁通密度見圖10，面的剖面圖和電磁鐵與船舶壁面接觸面的磁通分布見圖11。

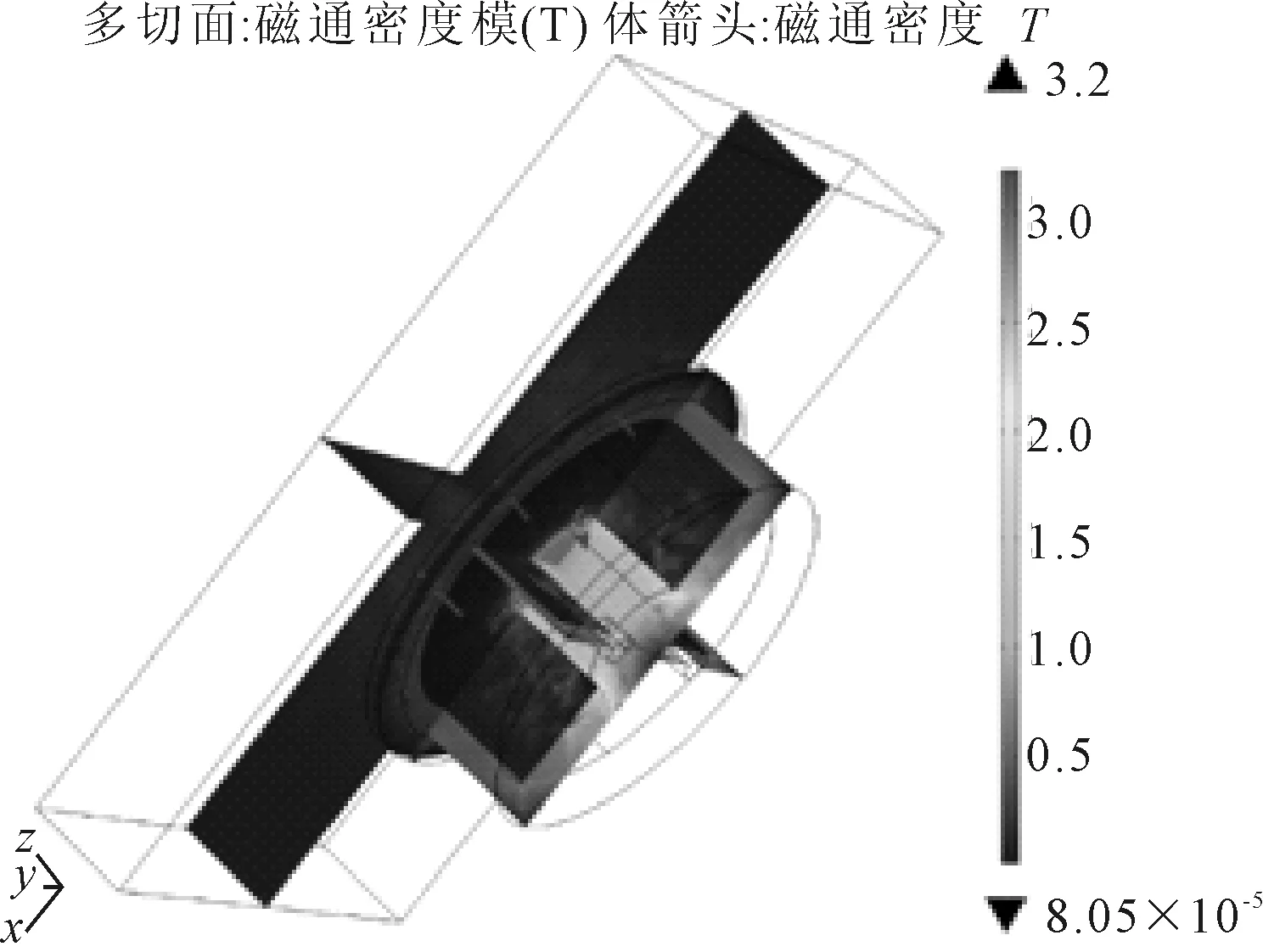
圖10 電磁鐵磁通密度三維視圖

圖11 電磁鐵各位置的磁通分布圖

從圖11a)可見，電磁鐵鐵芯位置集中了主要磁通量，在鐵板上產生的電磁力也最大，周圍的磁通則較為稀疏，相應的電磁力也更小。總體對比圖7a)和圖11a)的磁通量，電磁鐵的最大磁通量大于永磁鐵，這是由于電場的存在；從面上對比圖7b)和圖11b)，電磁鐵與壁面接觸時的接觸面上的最大磁通量為1.38 T，永磁鐵為1.21 T，因此，在適合機器人履帶的條件下，電磁鐵所能提供的最大吸附力稍大于永磁鐵。

同樣，在鐵板尺寸不變的情況下，以同樣的網格密度劃分、同樣的空氣空間，電磁鐵本身特性和電路內電流、電壓是不變的，間距屬于外在影響因素，改變電磁鐵與鐵板間距離，以1 mm距離的等差梯度為自變量，進行1～10 mm間距仿真，磁力變化情況見圖12。

圖12 電磁鐵的磁力隨間距的變化

由圖12可見，在間距為0 mm時取得最大電磁力為182.93 N，間距從0～3 mm的前期階段，電磁力迅速下降，與擬合指數趨勢類似，后期磁力變化放緩，但磁力很小，不能滿足要求，若磁力不足以使機器人吸附于壁面，可在現有的基礎上適當增大電流以達到磁力要求，與圖8對比，在同間距的情況下電磁鐵可產生的吸附力較大，一定程度上提高了越障能力。

4 結論

1)縱向傾覆為機器人臨界狀態，電磁鐵的最小磁力來源可由此作為依據，減小計算量。

2)建立電磁鐵和永磁鐵的有限元模型不同，控制方程和邊界條件隨之變化，電磁鐵最終所產生的吸附力大較大，能夠滿足機器人的安全吸附要求。建模時可將空氣的范圍盡量擴大，以貼近實際。

3)應力張量法所建立的有限元仿真模型模擬了磁力-間距變化情況，電磁鐵可以在安全吸附的前提下實現吸附力可調，電磁吸附方案在爬壁機器人作業領域是具有一定的應用價值的。