一類凸復合函數的共軛和次微分及應用

徐 剛，何丹露，馮世強

（西華師范大學 數學與信息學院，四川 南充 637000）

凸復合優化構成了一類非凸優化問題，引出了在現代優化模型理論和實踐中研究的各種優化模型，包括非線性規劃、非凸極大極小問題、非凸系統識別以及大規模數據分析和機器學習中的大多數非凸問題.在19世紀，就有學者對復合優化問題進行了研究.其中，Burke在1985年對復合不可微問題進行研究，提出了一類下降法［1］，并與Poliquin在1992年研究了非有限值凸復合函數的最優性條件［2］.

最近，因為凸復合優化問題對許多問題在現代優化、機器學習、大規模數據分析等方面具有重要性，許多學者又重新對這個問題產生了極大的興趣.其中，Duchi J C， Ruan F在2018年提出凸復合弱凸優化問題的隨機方法［3］，在2019年研究了魯棒相位檢索的復合優化［4］；Burke在2013年研究了上圖收斂光滑化及其在凸復合函數中的應用［5］，在2020年和Engle A研究了分段線性二次凸組合優化 karush-kuhn-tucker 映射的強度量（子）正則性及牛頓法的二次收斂性［6］，在2021年與Tim H以及Nguyen Q V基于下卷積研究了凸復合函數的共軛函數和次微分的性質［7］.

筆者將Burke，Tim和Nguyen的研究［7］推廣到一種帶算子的凸復合函數的形式，即：

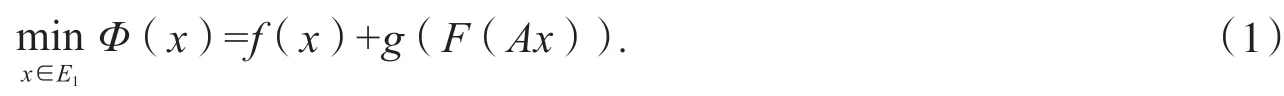
其中A是E1→E2的線性算子，F是E2→E3連續并且幾乎光滑的函數，f和g分別是E1→R∪｛+∞｝和E3→R∪｛+∞｝的非空閉凸函數.當A是單位算子時，Φ（x）就退化為原來的問題：

相比與式（2），式（1）的適用性更廣.

本文的主要工作有：在式（2）為式（1）的形式時，研究了凸復合函數的K-凸性質；函數由Φ1（x）變為Φ（x）時，Φ1（x）的共軛和次微分性質會發生怎樣的一個變化？問題（1）的最優解存在時，算子A需要滿足怎樣的性質？將結果應用到一個錐約束優化問題上，給出了錐約束問題最優解的存在性條件.

1 預備知識

E表示一個歐幾里得空間，其內積用〈·，·〉表示.對于A，B?E的Minkowski加法被定義為A+B=｛a+b|a∈A，b∈B｝，在這種情況下x+B∶=｛x｝+B，將實數域擴展為，假設L是E1→E2的線性映射，L的伴隨算子用L*表示.

集合K如果滿足λx∈K（λ≥0，x∈K），則K就是一個錐.K的極錐用K°表示，K°∶=｛v∈E|〈v，x〉≤ 0（x∈K）｝.K是凸錐當且僅當K+K?K；K是尖的當且僅當K∩-K=｛0｝.

根據文獻［8］中推論3.38，假設一個錐K?E，并且K是尖和凸的，則偏序關系被定義為x≤K yy-x∈K（x，y∈E）. 如果滿足條件x≤K +∞·，則對E附加一個最大元素+∞·，將E拓展到E·=E∪｛+∞·｝.

令K?E2，F∶E1→E2，F是凸函數當且僅當K-epiF=｛（x，v）∈E1×E2|F（Ax）≤Kv｝是凸的，所以F是K-凸的當且僅當F（A（λx+（1-λ）y））≤KλF（Ax）+（1-λ）F（Ay）.F（x）是K-凸的，則F（Ax）是K-凸的.假設C?E是一個凸集，C的仿射包用affC表示，相對內部用riC表示，C的水平錐被定義為. 函數f∶E→R的上圖epif∶=｛（x，a）∈E×R|f（x）≤a｝是凸的時候，f是凸函數.當函數f的上圖在E×R上是閉的，函數f是下半連續的.

根據文獻［9］，函數f的閉包是c1f，且：

特殊地，任何函數值取不到-∞的凸函數都是下半連續的，當且僅當函數等于它自己的閉包. 在本文中，把部分條件簡化為下面符號：Γ（E）∶=｛f∶E→R∪｛+∞｝|f是閉凸的｝，Γ0（E）∶=｛f∈Γ（E）|f是下半連續的｝.

函 數f∶E→R的fenchel共軛函數.被定義為，f的雙重共軛函數f **∶=（f *）*.根據文獻［9］的定理12.2可以知道對任意的凸函數f， c1f=f **.函數f在∈domf處的次微分是：.

并且f的次微分算子和共軛算子滿足Fenchel-Young不等式：

函數f的水平錐hznf∶=｛v|f（x+v）≤f（x）（x∈domf）｝，并且由文獻［9］中定理8.7可以得hznf= levf（a）∞，其中levf（a）∶=｛x∈E|f（x）≤a｝是f對于水平線a∈R的任意水平非空集.

函數f和g的最小卷積被定義為：

如果式（5）的最小值對所有的domf □ g=domf+domg都能取到，式（5）就可寫為：

引理1和引理2闡明了凸函數加法與最小卷積之間的共軛關系.

引理1令f，g∈Γ（E），則（c1f+c1g）*=c1（f *□g*）.若ri（domf）∩ri（domg）≠φ，則（f+g）*=（f *□g*），并對所有的y∈dom（f *□g*），有：.

給定閉凸函數g和線性映射F以及線性算子A得到（g°F°A）*=c1（A*F*g*）是函數（A*F*g*）（y）= inf｛g*∶（F°A）*=y｝的下半連續閉包.為確保結論成立，默認有效域是非空的，即A-1°F-1（ri（domg））≠φ成立［7］.

因此，當條件0∈ri（domg-F°A（domf））時可以得到關于問題：

引理2令式（1）的假設成立，如果F對于-hzng是凸的，即：

其中hzng∶=｛v∈E2|g（x+v）≤g（x）（x∈domg）｝，則Φ1是一個凸函數［7］.

令F∶E1→E3·，g∶E3→R∪｛+∞｝，A是一個線性算子，定義它們的復合函數為：

特殊地，給定v∈E3，則內積〈v，·〉∶，若x∈domF，

關于集合S?E的示性函數是：它的共軛函數是關于S的支撐函數δS∶E→R∪｛+∞｝，即：

2 K-凸性

本節主要對帶線性算子的復合函數的K-凸性進行研究，并得到了幾個重要結論，這幾個結論在第3節推導凸復合函數的次微分和分析最優解條件的推導過程中非常重要.

引理3令K?E3是凸錐，并且F∶E2→E3是有意義的并且是K-凸的映射，A是一個線性算子，則：ri（K-epiF°A）=｛（x，v）|x∈ri domF°A，F（Ax）≤riKv｝=（（riK）-epiF°A）∩（ri（domF°A）×E3）.

特殊地，如果domF=E1，則ri（K-epiF）=（riK）-epiF［7］.

定理 1假設K是一個錐，F∶E2→E3·，A是一個線性算子，如果K是閉凸的，那么F°A是K-凸的當且僅當〈v，F°A〉對所有的v∈-K°都是凸的.

證假設F是K-凸的，并且令v∈-K°，x，y∈domF=dom〈v，F〉 并且λ∈［0，1］， 因為λF（Ax）+ （1-λ）F（Ay）-F（A（λx+（1-λ）y））∈K，則可得到：

于是有：λ〈v，F〉（Ax）+（1-λ）〈v，F〉（Ay）=〈v，λF（Ax）+（1-λ）F（Ay）〉≥〈v，F（λAx+（1-λ）Ay）〉=〈v，F〉（A（λx+（1-λ）y））.

令x，y∈E1，λ∈［0，1］并且v∈-K°，因為〈v，F°A〉是凸的，所以：

于是：λF°A（x）+（1-λ）F°A（y）-F°A（λx+（1-λ）y）∈-（-K°）°=K，所以K是閉凸的，定理得證.

推論1令F∶E2→E3·，A是一個線性算子，K∈E3是一個閉凸錐，對于所有的（u，v）∈E1×E3，則下列式子成立：a.σK-epiF°A（u，v）=σgphF°A（u，v）+δK°（v）；b.σgphF°A（u，-v）=〈v，F°A〉*（u）；c.如果F是線性的，則〈v，F°A〉*=δ｛A*F*（v）｝.

證首先證明式a，由：

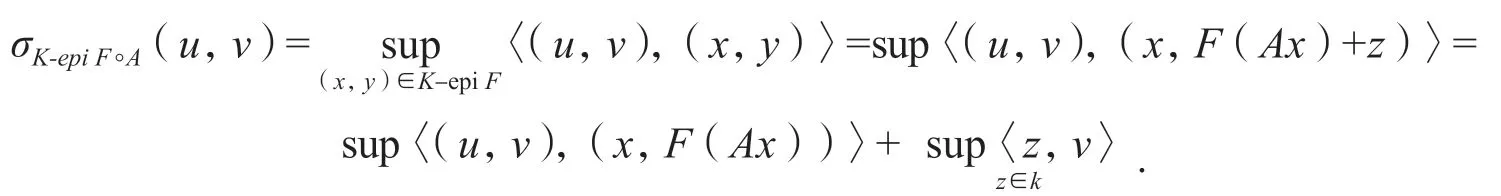
最后證明式c，由F是線性的可知：

接下來用到一個常用假設，這個假設來自于文獻［10］，即保證復合函數g°F°A是凸的需要滿足的條件是：

定理2令K是一個閉凸錐，假設F∶E2→E3使得｛〈v，F°A〉|v∈-K°｝?Γ0（E1），g∈Γ0（E3）并且是一個K-增的函數，A是一個線性算子，定義函數：

則ψ*（x，u）=g（u+F（Ax））.

證根據已知條件，可得：

結論得證.

3 帶結構復合函數的共軛和次微分

本節主要內容是通過基于簡單凸復合函數的共軛和次微分，進而推導出帶結構的凸復合函數的共軛和次微分.在整個過程當中使用了一個長期假設，即domF°A≠φ.

定理3假設K是一個閉凸錐，F是一個E2→E3的K-凸函數并且g∈Γ（E3），A是一個線性算子，同時g（F°A（x））≤g（y）（（x，y）∈K-epiF°A）， 則有結論：

①假如η（p）=+〈v，F°A〉*（p）， 則（g°F°A）*≤clη.特殊地，當v∈-K°，〈v，F〉∈Γ0（E2）， rgeF°A∩domg≠φ，g是下半連續并且是K-增時，等號成立，即（g°F°A）*=clη.

②如果有：

則結論①中的函數η是閉凸的，并且它的下確界就是最小值.

③如果結論②的假設成立，則（g°F°A）*（p）=+〈v，F°A〉*（p），并且.

證為證明結論①，首先定義一個函數γ∶E1×E3→R∪∶（x，y）→g（y），可以得到：

因此可發現：

則有：

結論②得證.

再證明結論③，根據結論①、結論②和引理1，得到：（g°F°A）*（p）=+〈v，F°A〉*（p）.

推論2假 設g∶，A是 線 性 算 子，則∈domg°F°A時，?（g°F°A）（）??〈v，F°A〉（x）. 特殊地，在定理3的假設下，等號成立.

證假設?〈v，F°A〉（x），則存在一個v∈?g（F°A（x））使得y∈?〈v，F°A〉（x）， 由于：

將y=F°A（x）（x∈E1）代入式（14）得到：

與式（15）相加可以得到：g（F°A（x））+〈y，x-x〉≤g（F°A（x））（x∈E1），這就表明y∈?（g°F°A）（x）.

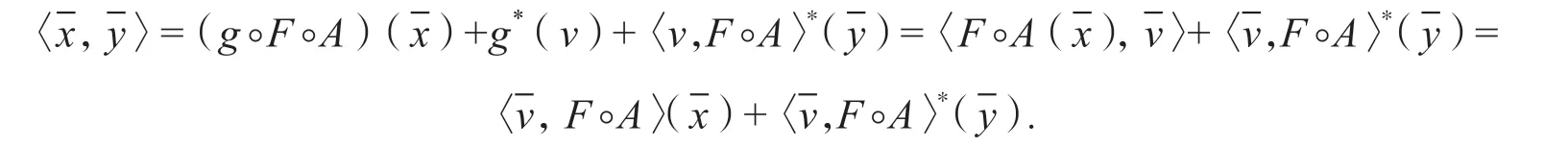
得到：y∈?（v，F°A）（x）.

定理4在定理3的假設下，， 當A*是滿射，A是單射時，等號成立.

證假設， 則使得x*=A*y*.于是有，所以，得到.當A*是 滿 射，A是 單 射 時，假 設，則x∈E1，所以，于是，因此x*∈A*?〈v，F〉（）.

推論3在定理3的假設下，令式（8）成立，f∈Γ（E1）并且有限制條件：

則有結論成立：

（Ⅱ）當x∈domf∩domg°F°A時，有：

證為證明結論（Ⅰ），定義函數g（x，y）∶=s+g（y）， 然后g∈Γ0（R×E3），并且有：

更多地，有：

現在證明充分性，令y∈?〈v，F°A〉（x）， 通過式（4）和式（20）得到：

因此存在v∈-k°使得：

并得到：

一方面，將Fenchel-yang不等式應用到g上，得到：， 應用到上，得到， 另一方面通過對偶性質可以得到：〈x，y〉≥f（x）+

則〈v，F°A（x）〉≥g（F°A（x））+g*（v），因此v∈?g（F°A（x））.由推論2可以得到：?（f +g°F°A）+又根據定理4可得到：A*?〈v，F〉（Ax）.

以下結論是對上面次微分結果的探究，主要研究滿足什么樣的性質時（18）能夠取等，并且遵循一個原則，即：

推論4假設K?E3是一個閉凸錐，函數F是一個E2→E3·的一個K-凸函數，A是一個線性算子，g∈Γ（E3）并且是K-增函數，同時使得條件（23）滿足，尤其是當A是單射，A*是滿射時，有：（g°F°A）*，且：

證由于g是K-增的，根據定理3和推論2，定理4得到結論.

推論5假設g∈Γ0（E3）， 并且函數F是一個E2→E3·的一個（-hzng）-凸函數，A是一個線性算子，A是單射，A*是滿射，同時F°A（ri（domF°A））∩ri（domg）≠φ， 于是：〈v，F°A〉*（p），且：

4 應用

考慮一般的問題，即：

其中f∈Γ（E1），F是K-凸的，并且K是一個閉凸錐，A是線性算子，根據推論4假設g=δ-k， 則問題（25）等價于：

δ-K是K-增的，如果v=-K，則u=u-v+v∈-K-K=-K， 因此在所有的有效域中：g（u）≤g（v），則充分條件（17）變為：

問題（25）和（26）的Fenchel-對偶問題是，Lagrange-對 偶問題 是

定理5假設K?E2是一個閉凸錐，F是E2→E3的一個K-凸函數，A是一個線性算子，如果條件（27）成立，則：

證由題可知，根據推論4得到：

定理6其中K是一個閉凸錐，F是E2→E3的K-凸函數，A是E1→E2的算子，則有：

滿足是（25）的最小值的充分條件.在條件（27）下，式（28）也是必要的.

證設g=δ-K，根據推論5和式（28），可得：0∈?（f+g°F°A）（x）， 所以x是f+g°F°A的最小值，同樣由推論5，?（f+g°F°A）（）等于右邊，于是結論得證.

5 結語

在本文中，基于最小卷積在弱假設（沒有較低的半連續性和弱單調性）的函數限定條件下，給出一類帶結構的復合函數的共軛和次微分及其對偶形式，并且將結果運用到錐約束問題上，探究了錐約束問題的最優性條件.本文的主要結果主要是第2～4節，是對Burke等人的結果的推廣，但相比于文獻［6］當中所研究的問題，本文所研究的帶結構的復合優化問題范圍更廣，所得到的共軛函數以及次微分的結果比文獻［6］的結果適用性更強.在以后的研究當中，希望可以將理論結果用在數值實驗當中，或者把帶結構的凸問題推廣到集值優化上.