具有時變通信延遲的多智能體系統改進蜂擁控制*
寇巧媛,袁 杰
(新疆大學電氣工程學院,新疆 烏魯木齊 830047)
1 引言
蜂擁行為是指大規模個體利用環境信息和簡單規則實現群體行為的現象。近年來,多智能體的蜂擁行為引起了諸如生物、物理、社會科學、計算機科學和控制工程等許多領域研究人員的關注[1]。多智能體系統協同控制主要包括一致性研究和蜂擁控制[2,3]研究。1987年,Reynolds[4]提出了鳥群蜂擁行為模型,其中包含了分離、聚合和避免碰撞3條基本規則。在Reynolds模型的基礎上,多種基于理想條件的蜂擁控制算法被相繼提出[5,6]。這些算法較好地實現了多智能體的位置一致和速度趨同。但是,由于多智能體系統本身具有非線性、網絡拓撲切換特性和通信延遲等問題[7],容易使協同現象退化甚至造成系統不穩定。因此,越來越多的研究人員將目光投向解決多智能體系統的實際應用上[8]。文獻[9]研究了具有有向固定拓撲圖上的高階不確定非線性多智能體系統一致性問題。文獻[10]利用拉普拉斯矩陣的性質和改進的包含控制,將一般線性多智能體系統控制問題轉化為離散時間線性切換系統的穩定性問題。文獻[11]研究了定向交互拓撲下分數階多智能體系統的分布式控制,提出了具有絕對阻尼和通信時延的控制規律。文獻[12]考慮了具有非周期性間歇通信拓撲的線性多智能體系統的一致性,利用兩跳鄰居信息設計了間歇通信拓撲控制規律。文獻[13]利用人工勢函數和狀態觀測器設計控制方案,解決具有外部干擾的多智能體系統蜂擁問題。動態多智能體系統的通信時延問題已經引起了許多研究人員的關注[14,15]。文獻[16]研究了復雜環境下固定通信時延多智能體的蜂擁控制。文獻[17]研究了具有通信時延的多智能體系統的蜂擁控制問題,其只考慮了速度信息的時滯,并沒有考慮位置信息的時滯。
當網絡結構不連通時,系統將具有不同的網絡延遲[17]。因此在實際應用中,不僅要考慮網絡信息阻塞引起的未知通信時延,還要考慮異構拓撲造成的時延。此外,在目前諸多研究中,通信時延上限均作為已知條件使用,尚未有研究人員研究在復雜環境中存在時變通信時延的不確定非線性二階多智能體系統的蜂擁控制。
針對上述問題,本文在具有時變通信時延的不確定非線性二階多智能體系統中利用魯棒自適應算法設計了滿足速度匹配和位置跟隨的控制規律,使多智能體系統實現蜂擁行為;同時利用Lyapunov-Krasovskii方法構造能量函數,證明了采用本文提出的控制規律能確保多智能體系統網絡始終連通,群體速度收斂于虛擬領導者的速度,智能體之間不會發生碰撞,并且當通信延遲滿足一定要求時多智能體系統趨于穩定;最后通過實驗驗證了本文設計的魯棒自適應算法能夠實現二階多智能體系統的蜂擁控制,在保證位置跟隨和速度匹配的同時,增強了二階多智能體系統的抗干擾能力。
2 預備知識
2.1 基本定義
令R,R+,Rd,RN×N分別代表一維實空間、一維正實空間、d維實向量和N×N維實矩陣。Id表示d維的單位矩陣。r表示智能體的傳感器半徑,R表示智能體的交互半徑,‖·‖1表示1范數,‖·‖表示2范數,即歐氏距離。
2.2 圖論知識
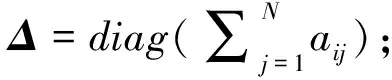
3 控制規律設計和穩定性證明
3.1 不確定非線性二階多智能體系統運動學模型
在d維噪聲環境中,由N個節點組成的二階多智能體系統包含了一個虛擬領導者(運動學模型中下標為0)和N-1個智能體(運動學模型中下標為1,2,…,N-1)。第i個智能體運動學模型描述如式(1)所示:
(1)
其中,初始值表示如式(2)所示:
(qi,pi)(0)=:(qi0,pi0),i=1,…,N-1
(2)
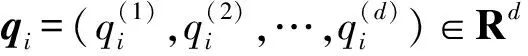
(3)
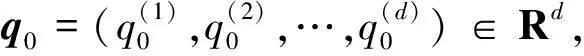
非線性動力學函數f(·)和擾動φ(·)滿足局部Lipschitz連續條件[16],即對于所有的p1(t),p2(t)∈Rd且θ,γ為非負常數,滿足式(4):
(4)
假設1初始G(0)是連通圖。
假設2虛擬領導者的控制規律輸入是有界的,即?κ>0,使得‖f(p0(t))+φ(p0(t))‖<κ<∞。
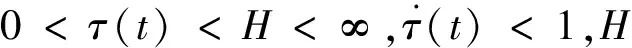
3.2 控制規律設計
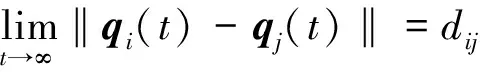
ui(t,τ(t))=u1i+u2i+u3i+u4i
(5)
(6)
u1i為人工勢函數,采用文獻[19]的定義,如式(7)所示:
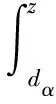
(7)
其中,
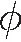
(8)
(9)
(10)
其中,h∈(0,1),ω>0,ψα(z)滿足式(11):
▽qiψα(‖qij(t)‖σ)=▽qijψα(‖qij(t)‖σ)=
-▽qjψα(‖qij(t)‖σ)
(11)

i,j=1,2,…,N-1
(12)
其中,βij,mi,ni,li,ηi為任意正實數,各個參數初始值設定如式(13)所示:
(13)
3.3 穩定性證明與分析
定理1考慮具有時變通信延遲的不確定非線性二階多智能體系統的運動學模型如式(1)和式(3)所示,輸入控制如式(5)和式(6)所示,人工勢函數如式(7)所示,假設1至假設3成立,初始能量Q0是一個有限值,則有以下結論成立:
(1)當t≥0時,多智能體系統網絡圖G(t)滿足連通性。
(3)智能體之間不會發生碰撞。
(14)
證明一般地,在tk時刻,圖G(0)切換到圖G(k)。令t(0)=0,在t∈[t(0),tk)根據Lyapunov-Krasovskii方法構造能量函數Q(t)如式(15)所示(具體推導過程見附錄):
(15)
Q(t)對時間t求導,且根據假設1和young不等式[15]:2xTy≤xTPx+yTP-1y可得到式(16):
(16)
對于任意x∈Rd,滿足不等式‖x‖≤‖x‖1[20],可得式(17)和式(18):
(17)
(18)
Q(t+tk)≤Q0+mψ(‖qij(t)‖α)≤Qmax
(19)
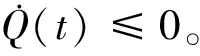
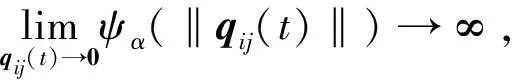
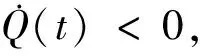
□
4 仿真分析
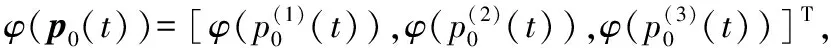
利用控制規律式(5)和式(6)得到的三維軌跡以及不同迭代次數下智能體位置、速度如圖1示。從圖1可以看出,在多智能體系統移動過程中智能體之間能夠形成緊密的晶格狀網絡;智能體之間保持強連通和集群構型的穩定;各個智能體的速度方向和大小趨于一致,并與虛擬領導者保持同步;各個智能體位置趨于虛擬領導者位置。
圖2為Laplacian矩陣特征值和各參數調節圖。其中,圖2b~圖2f展示了魯棒自適應控制算法調節各個參數的變化情況,可以看出當迭代次數達到200時,多智能體系統中各個參數趨于平穩,根據魯棒自適應參數的定義可知,此時系統集群和跟隨情況已經趨于穩定和收斂。圖1所示的多智能體系統的運動軌跡和不同參數下智能體的位置和速度,表明對應時刻的智能體之間已經形成穩定的晶格狀構型,智能體速度與虛擬領導者速度達成同步,群體中心位置收斂于虛擬領導者位置,這與魯棒自適應參數曲線相一致。圖2a中Laplacian矩陣特征值隨時間變化的情況也證實了隨著時間t的推移,多智能體系統的網絡一直保持強連通。
為了檢驗本文所提出的控制規律對外界未知干擾和時變通信時延的魯棒性,分別選取不同信號干擾強度ξ和時變通信時延強度參數τm進行對比實驗。考慮時間對系統時滯的影響,選取τ(2)=τme-5tsin2(t)作為多智能體系統的時變通信時延函數。設定時變通信時延調節參數τm為0.1,0.2,0.3,0.4,0.5。在不同強度通信時延下分別進行100次實驗,系統速度誤差ε小于0.02時認為控制規律收斂。實驗結果如圖3和表1所示,其中圖3a和圖3b驗證了多智能體系統在不同強度的時變通信延遲下網絡系統能夠快速收斂,并且智能體與虛擬領導者的速度誤差不斷減少,同時各智能體相對虛擬領導者的位置保持穩定。表1表明時變通信時延的強度并不影響系統的收斂速度。
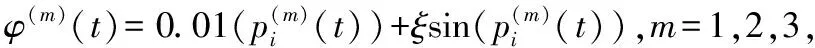
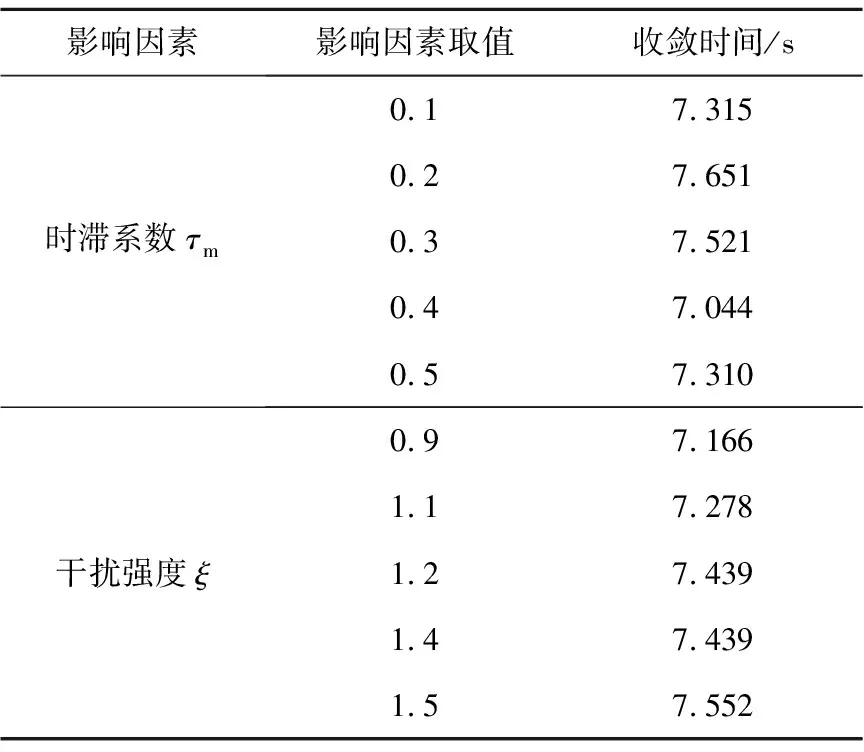
Table 1 Convergence time of system error
5 結束語
本文提出具有時變通信時延的多智能體系統的魯棒自適應蜂擁控制規律,并對自帶不確定非線性二階多智能體系統模型進行驗證,通過仿真實驗得出以下結論:在外界干擾和通信時延同時存在時,動態多智能體系統可以保持較好的晶格狀網絡,維持較強的連通性,智能體的位置和速度都收斂于虛擬領導者。當時變通信時延滿足一定條件時,魯棒自適應蜂擁控制規律可使多智能體系統收斂并達到穩定。在不同強度干擾下,系統可快速收斂并形成穩定的拓撲結構。因此,采用魯棒自適應設計的蜂擁控制規律可使系統具有較強的適應能力和魯棒特性。然而,多智能體系統在通信時延下選取關鍵子網節點還沒有明確的控制設計方案,如何利用復雜網絡特性設計蜂擁控制方案,以提高多智能系統信息傳遞效率是下一步研究重點。
Q(t)=Qi1(t)+Qi2(t)+Qi3(t)+Qi4(t)=
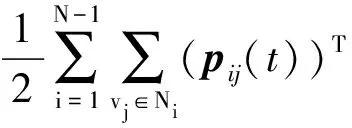
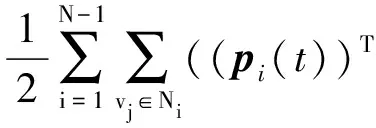
(pj(t))T?qij(t)ψα(‖qij(t)‖σ))=

(pj(t))T?qjψα(‖qij(t)‖σ))=

(pj(t))T?qiψα(‖qij(t)‖σ))=
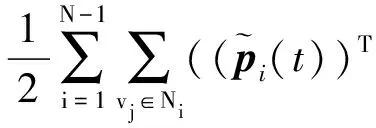
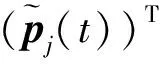
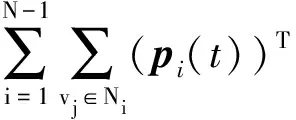
f(p0(t))-φ(p0(t)))=
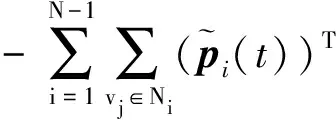
f(p0(t))-φ(p0(t)))
對于任意x∈Rd,滿足不等式‖x‖≤‖x‖1[19],可得:
根據young不等式[18]:2xTy≤xTPx+yTP-1y可得到:

