非Hermitian正定線性方程組的外推的廣義HSS方法*

吳思婷，鮑 亮

(華東理工大學數學學院,上海 200237)

1 引言

大型稀疏線性方程組在許多科學與工程領域都有著非常重要的作用，比如在最優化問題、流體力學和電磁學等領域都需要對此類問題進行求解[1-7]。因此，如何快速有效地求解大型稀疏線性方程組已經成為當下非常重要的課題之一。

本文考慮如式(1)所示的大型稀疏正定線性方程組的求解：

Ax=b

(1)

其中,A∈Cn×n為非Hermitian正定矩陣，x∈Cn為未知向量，b∈Cn為已知向量。當方程組(1)的系數矩陣規模較小時，使用直接法更加方便。而對于較大規模的稀疏非Hermitian正定線性方程組，研究人員一般采用迭代法進行求解。

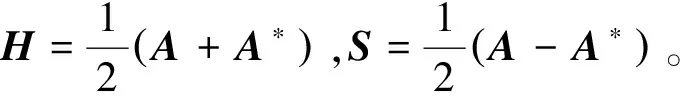
在求解某些特定問題時，求解系數矩陣αI+S的線性方程組可能會出現一些問題，甚至可能會同求解原始的線性方程組Ax=b一樣困難。而選擇恰當的矩陣K會使得矩陣αI+K+S比矩陣αI+S更對角占優，因此求解系數矩陣αI+K+S的線性方程組會比求解系數矩陣αI+S的線性方程組更加方便。基于上述發現，本文將系數矩陣進行廣義的HS分裂，再進行非對稱的二步迭代。這可以將二步迭代中求解系數矩陣αI+S的線性方程組簡化為求解系數矩陣αI+K+S的線性方程組，大大加快了迭代方法的收斂速度。

本文將系數矩陣進行廣義的Hermitian和反Hermitian分裂，再通過引入新的變量同時結合外推的技術，給出一種外推的廣義Hermitian和反Hermitian迭代方法EGHSS(Extrapolated and Generalized HSS)。還理論分析了本文方法的收斂性，給出了該方法收斂的充要條件，并將該方法迭代矩陣的譜半徑與GHSS方法迭代矩陣的譜半徑和EHSS方法迭代矩陣的譜半徑進行比較。數值實驗結果表明，在處理某些實際問題中，EGHSS迭代方法比GHSS迭代方法和EHSS迭代方法更有效，且在合適的參數值下新方法的收斂效率可以大大提高。

2 EGHSS迭代方法

首先簡要回顧EHSS迭代方法[13]。

方法1EHSS迭代方法。

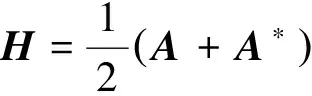
(2)

其中,α>0和ω>0均為給定的常數。

事實上，可以將式(2)改寫成如式(3)～式(5)所示的等價形式：

x(k+1)=M1(α,ω)x(k)+N1(α,ω)b,

k=0,1,2,…

(3)

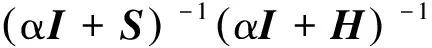
[HS-(1-ω)α(H+S)+α2I]

(4)

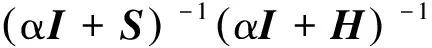
(5)

這里的M1(α,ω)是EHSS迭代方法的迭代矩陣。

考慮到上述迭代方法中求解系數矩陣為αI+S的線性方程組仍有一定的難度，為了將其簡化為求解系數矩陣αI+K+S的線性方程組，本文將HS分裂中的Hermitian矩陣H作如式(6)所示的分裂：

H=G+K

(6)

其中，G和K為Hermitian半正定矩陣，從而得到系數矩陣A∈Cn×n有如式(7)所示廣義的HS分裂：

A=G+K+S

(7)

其中，G和K為Hermitian半正定矩陣，S為反Hermitian矩陣。一種常見的矩陣分裂格式如式(8)所示：

(8)

基于上述系數矩陣的廣義HS分裂，下面介紹EGHSS迭代方法。

方法2EGHSS迭代方法。

設A∈Cn×n為非Hermitian正定矩陣，給定一個初始向量x(0)∈Cn，對于k=0,1,2,…, 直到迭代序列{x(k)}收斂，計算如式(9)所示：

(9)

其中,α>0和ω>0均為給定的常數。

當ω=0時，EGHSS迭代方法就成為GHSS迭代方法；當K=0時，EGHSS迭代方法就成為EHSS迭代方法；當ω=0且K=0時，EGHSS迭代方法就成為HSS迭代方法。

觀察EHSS方法的迭代格式，不難發現式(9)等價式(10)～式(12)所示的矩陣-向量形式：

x(k+1)=M(α,ω)x(k)+N(α,ω)b,k=0,1,2,…

(10)

M(α,ω)=(αI+K+S)-1[K+S-(1-ω)αI+

(2-ω)α(αI+G)-1(αI-K-S)]=

(αI+K+S)-1(αI+G)-1{(αI+G)[K+

S-(1-ω)αI]+(2-ω)α(αI-K-S)}=

(αI+K+S)-1(αI+G)-1{G(K+S)-

(1-ω)α(G+K+S)+α2I}

(11)

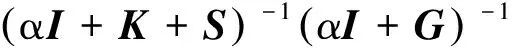
(12)

這里的M(α,ω)為EGHSS迭代方法的迭代矩陣。

當然EGHSS迭代方法也可由系數矩陣A經過如式(13)～式(15)所示的分裂得到：

A=B(α,ω)-C(α,ω)

(13)

(14)

(1-ω)α(G+K+S)+α2I]=

(15)

3 收斂性分析

本節討論了EGHSS迭代方法的收斂性，并給出了迭代方法收斂的充要條件。

引理1[12]設A∈Cn×n為正定矩陣，令A=G+K+S,G和K為Hermitian半正定矩陣，S為反Hermitian矩陣，M(α)為GHSS迭代方法的迭代矩陣。如果G或K為正定矩陣，且α>0，則迭代矩陣M(α)的譜半徑ρ(M(α))滿足式(16)：

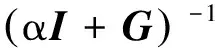
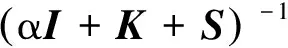
(16)

即GHSS迭代方法收斂到線性方程組式(1)的精確解x*∈Cn。

從上述EGHSS方法的迭代格式推導過程不難發現，EGHSS方法的迭代矩陣與GHSS方法的迭代矩陣存在一定的關系。為了證明EGHSS迭代方法的收斂性，本節根據EGHSS迭代方法的迭代矩陣M(α,ω)的形式，進一步分析了EGHSS迭代方法的迭代矩陣M(α,ω)與GHSS迭代方法的迭代矩陣M(α)之間的關系。

定理1設A∈Cn×n為非Hermitian正定矩陣，令A=G+K+S,G和K為Hermitian半正定矩陣，S為反Hermitian矩陣，對任意的α>0和ω≥0，GHSS迭代方法的迭代矩陣如式(17)所示：

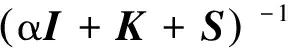
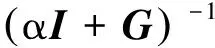
(17)

那么EGHSS迭代方法的迭代矩陣M(α,ω)滿足式(18)：

(18)

證明

ωI+(2-ω)M(α)=

ωI+(2-ω)(αI+K+S)-1(αI-G)

(αI+G)-1(αI-K-S)=

(αI+K+S)-1(αI+G)-1[ω(αI+G)

(αI+K+S)+(2-ω)(αI+G)(αI-G)(αI+G)-1

(αI-K-S)]=(αI+K+S)-1(αI+G)-1

[ω(αI+G)(αI+K+S)+

(2-ω)(αI-G)(αI+G)(αI+G)-1

(αI-K-S)]=(αI+K+S)-1(αI+G)-1

[ω(α2I+αG+αK+αS+GK+GS)+(2-ω)

(αI-G)(αI-K-S)]=(αI+K+S)-1(αI+G)-1

[2GK+2GS+2α2I-2(1-ω)α(G+K+S)]

從而可以得到式(19)：

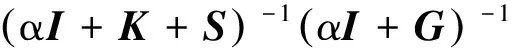
[G(K+S)-(1-ω)α(G+K+S)+α2I]=

(19)

□

由引理1和定理1可以得出EGHSS迭代方法收斂的充要條件。

定理2[14,15]設A∈Cn×n為非Hermitian正定矩陣，令A=G+K+S,G和K為Hermitian半正定矩陣，S為反Hermitian矩陣，如果0≤ω<2，那么對任意的α>0，EGHSS方法的迭代格式式(9)收斂。

證明由定理1知EGHSS迭代方法的迭代矩陣M(α,ω)與GHSS迭代方法的迭代矩陣M(α)之間存在如式(20)所示的關系：

(20)

設λ和μ分別為GHSS迭代方法的迭代矩陣M(α)和EGHSS迭代方法的迭代矩陣M(α,ω)的特征值，則有式(21):

(21)

若λ為實數，則式(22)成立:

(22)

若λ為復數，設λ=a+bi,i為虛數單位，則式(23)成立:

(23)

綜上所述,式(24)成立：

(24)

又由引理1知?α>0，ρ(M(α))<1,所以當0≤ω<2時，即0<2-ω≤2時，有式(25):

(25)

因此,EGHSS迭代方法收斂。

□

由定理2可知，EGHSS迭代方法是條件收斂的。由定理2的證明過程可知，EGHSS方法的迭代矩陣M(α,ω)的特征值與GHSS方法的迭代矩陣M(α)的特征值存在著一定的聯系。接下來進一步分析EGHSS方法的迭代矩陣M(α,ω)的譜半徑與GHSS方法的迭代矩陣M(α)譜半徑之間的關系。

定理3設A∈Cn×n為非Hermitian正定矩陣，令A=G+K+S,G和K為Hermitian半正定矩陣，S為反Hermitian矩陣，λ=a+bi為GHSS方法的迭代矩陣M(α)的特征值，則有：

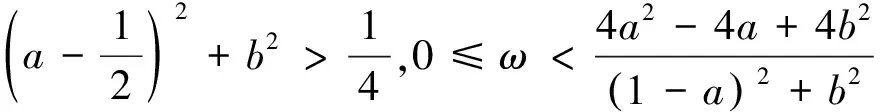
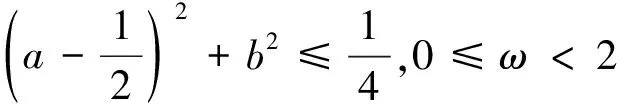
證明根據定理2可得式(26):

(26)

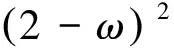
(27)

(28)

此時|μ|<|λ|，于是當a2+b2<1時，有0≤ω<2，則式(29)成立:

ρ(M(α,ω))≤ρ(M(α))<1

(29)

ρ(M(α))≤ρ(M(α,ω))

(30)

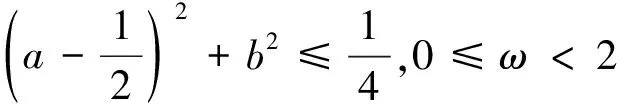
ρ(M(α))≤ρ(M(α,ω))<1

(31)

□

根據定理3可知，通過選擇合適的參數，EGHSS方法的迭代矩陣M(α,ω)的譜半徑會小于GHSS方法的迭代矩陣M(α)的譜半徑。下一節將通過具體的數值實驗對EGHSS迭代方法、GHSS迭代方法和EHSS迭代方法的收斂速度和迭代次數進行比較，并詳細分析矩陣規模、α和ω對EGHSS迭代方法收斂速度的影響。

4 數值實驗

本節對EGHSS迭代方法進行了數值實驗，并將其結果與GHSS迭代方法和EHSS迭代方法進行比較。本次數值實驗是在英特爾四核處理器(2.40 GHz，8 GB RAM)環境下應用Matlab編程語言實現的。

例1考慮文獻[16]中的數值例子,如式(32)所示：

-u″+qu′=f

(32)

邊界條件為齊次邊界條件。根據中心差分方法對式(32)進行離散，可以得到如式(33)所示的系數矩陣：

A=tridiag(-1+qh/2,2,-1-qh/2)∈RN×N

(33)

其中，tridiag(·,·,·)表示三對角矩陣。

例2考慮區域為Ω=[0,1]×[0,1]×[0,1]的一類三維對流擴散方程[8],如式(34)所示：

-(uxx+uyy+uzz)+q(ux+uy+uz)=

f(x,y,z)

(34)

其中,q=1000為給定常數，且區域邊界滿足Dirichlet邊界條件。下面采用向前差分離散方程得到如式(35)所示的系數矩陣：

A=Tx?I?I+I?Ty?I+

I?I?Tz∈RN3×N3

(35)

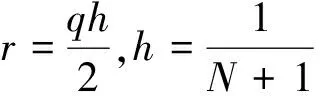
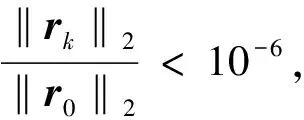
4.1 收斂速度分析

表1～表3分別給出了例1中GHSS迭代方法、EHSS迭代方法和EGHSS迭代方法的收斂迭代次數和收斂時間，并且給出了3種迭代方法近似最優變量的取值。其中N的取值表示的矩陣規模分別為256×256階，512×512階,1024×1024階，2048×2048階。從表1～表3可以發現，當數值例子相同且矩陣規模相同時，EGHSS迭代方法的譜半徑、迭代次數和迭代時間普遍都小于GHSS迭代方法的和EHSS迭代方法的。且隨著qh和N的不斷增大，EGHSS迭代方法的迭代矩陣譜半徑、迭代次數和迭代時間都遠遠小于GHSS迭代方法的和EHSS迭代方法的。因此，不難從表1～表3中發現，在合適參數下EGHSS迭代方法會相比GHSS迭代方法和EHSS迭代方法有更好的效果。

表4給出了例2中GHSS迭代方法、EHSS迭代方法和EGHSS迭代方法的收斂迭代次數和收斂時間，并且給出了3種迭代方法近似最優變量的取值。其中N的取值表示的矩陣規模為1728×1728階和4096×4096階。從表4可以發現，當矩陣規模相同時，EGHSS迭代方法的迭代速度比GHSS迭代方法的和EHSS迭代方法的更快。甚至當迭代次數相近時，EGHSS迭代方法的迭代時間明顯小于GHSS迭代方法的。因此不難發現，在選擇合適參數下EGHSS迭代方法會相比GHSS迭代方法和EHSS迭代方法有更好的效果。

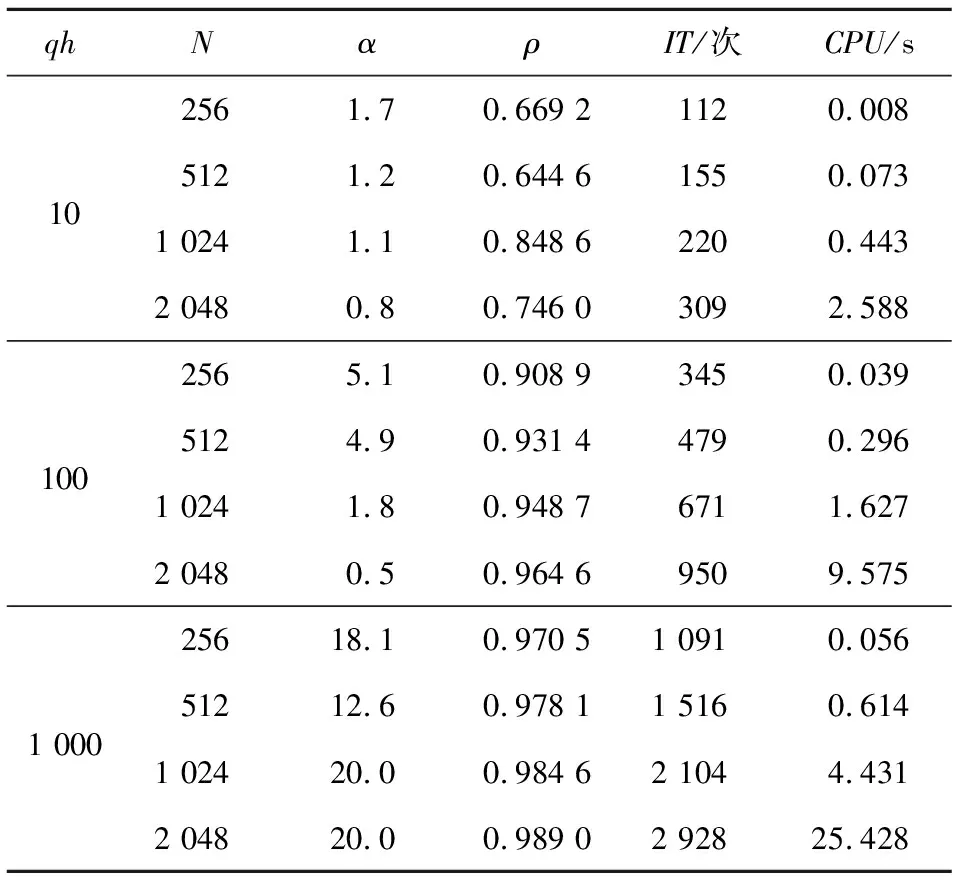
Table 1 IT and CPU of GHSS iterative method for example 1

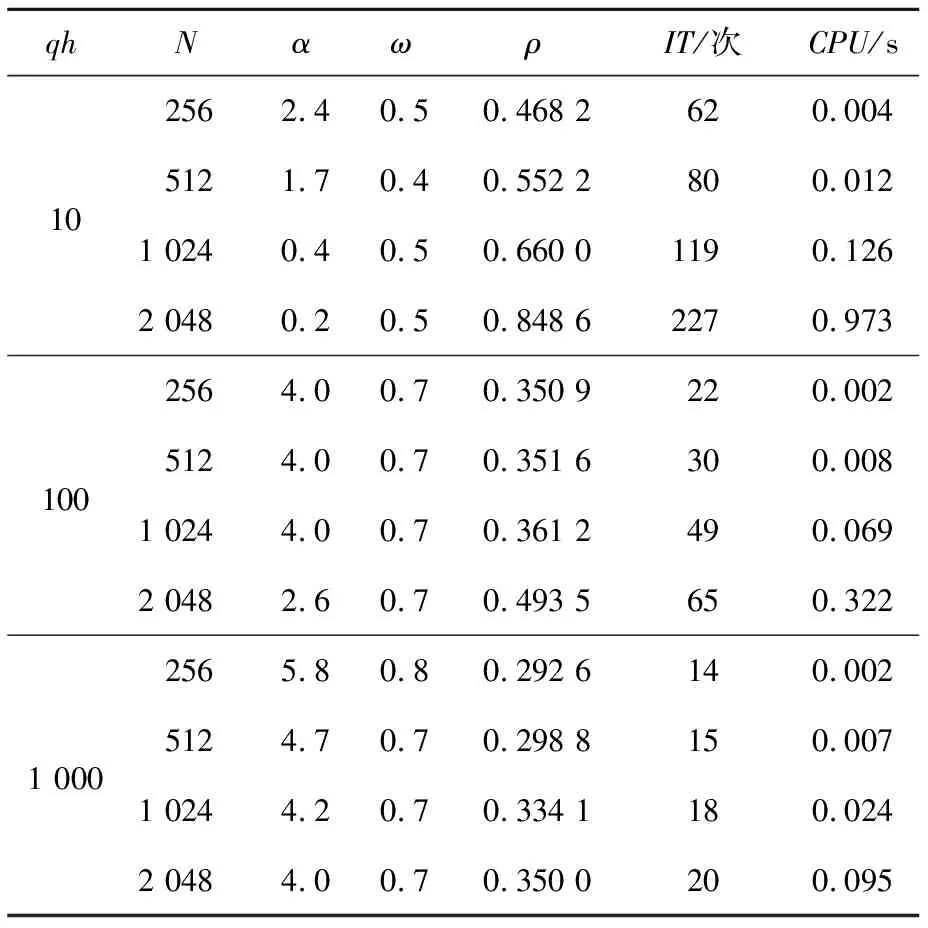
Table 2 IT and CPU of EHSS iterative method for example 1

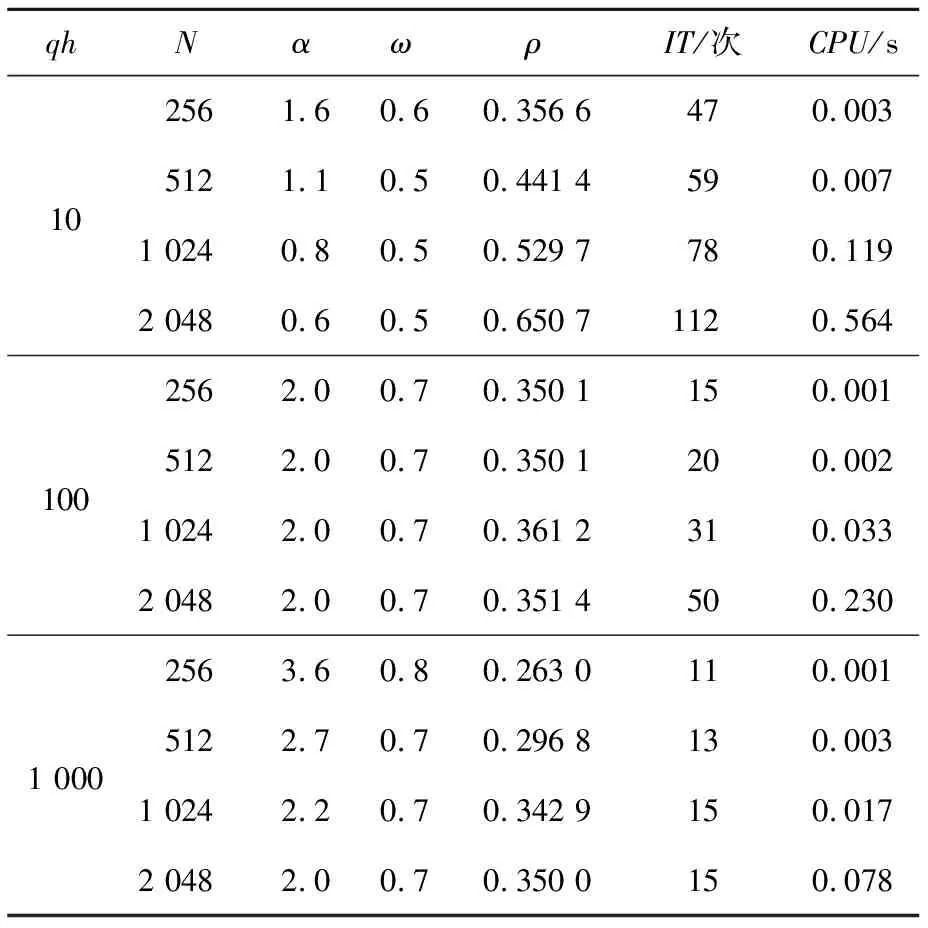
Table 3 IT and CPU of EGHSS iterative method for example 1

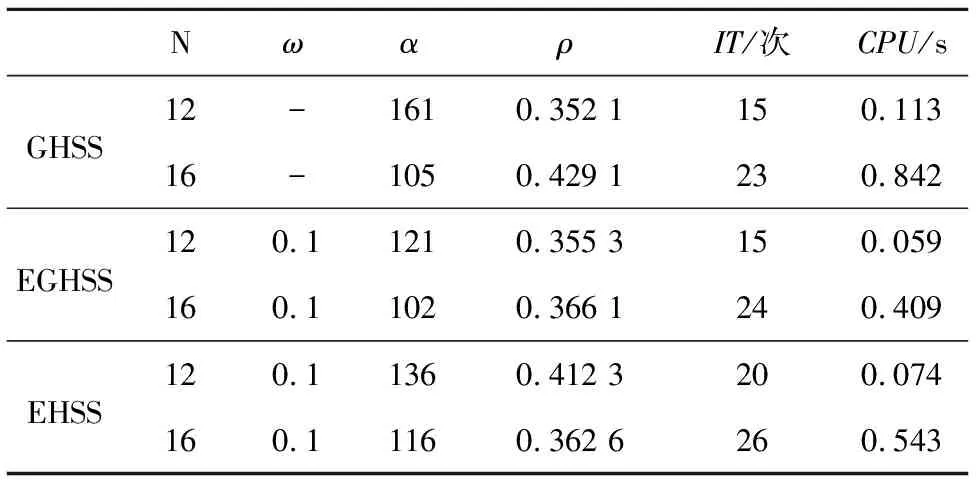
Table 4 IT and CPU of GHSS,EGHSS and EHSS iterative method for example 2

圖1展示了例1取qh=10時，系數矩陣規模分別為256×256階和512×512階的情況下，EGHSS迭代方法、GHSS迭代方法和EHSS迭代方法的殘量隨著迭代步數的變化趨勢。顯然EGHSS迭代方法的殘量下降曲線位于GHSS迭代方法和EHSS迭代方法的殘量下降曲線之下。這說明對上述qh=10的數值例子，EGHSS迭代方法相較于GHSS迭代方法和EHSS迭代方法迭代次數更少，迭代時間更短。并且系數矩陣規模越大，EGHSS迭代方法相較于其他2種方法的優勢越明顯。因此，在處理某些實際問題中，EGHSS迭代方法比GHSS迭代方法和EHSS迭代方法具有迭代次數更少、迭代時間更短等優點。

4.2 參數α和ω的靈敏度分析

通常來說，迭代矩陣的譜半徑越小，迭代方法的收斂速度越快。因此，本節主要討論各個變量對EGHSS方法的迭代矩陣譜半徑的影響。首先分析單一變量α對EGHSS迭代方法、GHSS迭代方法和EHSS迭代方法的迭代矩陣譜半徑的影響；再分析2個變量α和ω共同對EGHSS迭代方法的譜半徑的影響。本節參數靈敏度分析僅考慮例1中的參數α和ω對EHSS迭代方法譜半徑的影響。

圖2a表示例1選取矩陣規模為256×256階，且qh=10和ω=0.6時，EGHSS迭代方法、GHSS迭代方法和EHSS迭代方法中參數α與迭代矩陣譜半徑的關系。圖2b表示例1選取矩陣規模為512×512階，且qh=10,ω=0.5時，EGHSS迭代方法、GHSS迭代方法和EHSS迭代方法中參數α與迭代矩陣譜半徑的關系。觀察圖2可以發現，3種方法迭代矩陣的譜半徑均隨著α增大先減小后增大。除此之外,EGHSS迭代方法的最小譜半徑明顯小于GHSS迭代方法和EHSS迭代方法的最小譜半徑(都小于1)，這說明了EGHSS迭代方法相比GHSS迭代方法和EHSS迭代方法有更好的迭代效果。

圖3a表示例1選取系數矩陣規模為256×256階且qh=10時，EGHSS迭代方法中的參數α和ω與迭代矩陣譜半徑的關系。圖3b表示例1選取系數矩陣規模為512×512階且qh=10時，EGHSS迭代方法中的參數α和ω與迭代矩陣譜半徑的關系。觀察圖3可以發現，當α和ω處于一個適當的取值范圍時，EGHSS迭代方法的譜半徑小于1，符合定理2的收斂性證明。當系數矩陣規模為256×256階且qh=10時，α=1.6和ω=0.6時,EGHSS迭代方法的譜半徑近似取得最小值(小于1)。當系數矩陣規模為512×512階且qh=10時，α=1.1和ω=0.5時,EGHSS迭代方法的譜半徑近似取得最小值(小于1)。因此,圖3a和圖3b分別選擇ω=0.6和ω=0.5是合理的。

5 結束語

本文提出了一種求解大型稀疏非Hermitian正定線性方程組的EGHSS迭代方法，給出了該方法收斂的充要條件，并進行了數值實驗。在與GHSS迭代方法和EHSS迭代方法的譜半徑、迭代步數及迭代時間的比較過程中不難發現，EGHSS迭代方法在處理某些問題時相較于其他2種迭代方法具有一定的優越性。除此之外，本文還分析了單一參數α對EGHSS方法迭代矩陣譜半徑的影響，以及2個參數α和ω共同對EGHSS方法迭代矩陣譜半徑的影響。當然，理論上的最優參數α和ω的確定還有待進一步的研究。總的來說，EGHSS迭代方法是一種較GHSS迭代方法和EHSS迭代方法更有競爭力的方法，特別是選取了合適的參數α和ω后，EGHSS方法的收斂速度大大提高。