訪問策略隱匿的可追責層次屬性加密方案*

唐廣鎮,陳 卓

(湖北工業大學計算機學院,湖北 武漢 430068)

1 引言

隨著云技術的迅猛發展，廣大企業和個人開始選擇云服務商的服務實現計算和存儲。但是，在將海量計算和存儲轉移到云端的同時，云服務商通常是不受信任的，因此有效解決云端數據安全問題成為云服務突破發展瓶頸的重要手段[1]。密文策略屬性加密CP-ABE(Ciphertext-Policy Attribute-Based Encryption)[2]的創造性提出為實現用戶的細粒度訪問和云端數據的保密提供了新的思路，眾多研究人員對CP-ABE方案的功能從不同方面進行了拓展。

在傳統的CP-ABE方案中，沒有對違規行為進行追責，用戶會為了利益違規地將私鑰共享給具有相同屬性集的多個用戶，因此追責泄露私鑰的違規用戶是提高CP-ABE方案安全性的一個重要步驟。另外，解密者接收到的密文包含訪問策略，加密者的信息通常嵌在顯性策略中，存在信息被違規用戶泄露的可能性，因此隱匿訪問策略也十分重要。

Waters等[3]首次用秘密同享方案表達訪問策略。Zhang等[4]在合數階群下提出了一種滿足廣域的半策略隱匿方案。許盛偉等[5]和閆璽璽等[6]都提出了多權威層次授權的方案，均可以隱匿策略。Wu等[7]提出了一種可追責的方案，能讓第三方追溯私鑰的來源。Yadav等[8]提出了一個具有高表達力的方案，能對濫用密鑰的用戶進行白箱追責，但計算開銷較大。Ning等[9]在合數階群下也提出了能進行白箱追責的方案，而且存儲開銷小。馬瀟瀟等[10]提出了滿足廣域的可追蹤方案。Khan等[11]在方案中運用隱匿向量加密技術,實現了完全隱匿。但是以上方案中，文獻[4-6]方案不支持密鑰的追責，文獻[8-10]方案不支持訪問策略的隱匿。為此，王梅等[12]提出了一種支持密鑰追責和策略隱匿的方案，公鑰和主密鑰會略有增長。Li等[13]實現的隱匿策略方案能夠進行黑箱追責且采用多權威機構授權。Changhee等[14]實現的隱匿策略方案能夠進行白箱追責。石宇清等[15]提出了一種支持白箱追責的廣域隱匿方案。文獻[13,14]方案的實現均基于素數階，提升了計算效率，但訪問結構用多值與門表達，訪問策略的安全性和表達力稍弱。胡媛媛等[16]提出的隱匿訪問策略方案，融合了密文搜索和代理重加密技術，但不支持用戶追責。

針對密鑰泄露和訪問策略顯性暴露的問題，本文基于樹訪問結構，在合數階雙線性群下提出了一種可隱匿策略且可追責私鑰的層次屬性加密方案THH-CP-ABE(Traceable Hierarchical Hidden Ciphertext-Policy Attribute-Based Encryption)，并證明了本文方案在完全安全模型下是選擇明文安全。本文方案的特點如下所示：

(1)策略隱匿。訪問策略中插入合數階子群中的隨機元素，以合數階子群的正交特性，隱匿訪問策略。

(2)可追責。將用戶標識加入其私鑰運算中，可對違規用戶追責。

(3)層次授權。使用層次授權體系，避免根權威的負荷過重和風險過高，提高了安全性和效率。

(4)高表達力。用樹訪問結構表達訪問結構，提高了表達的靈活性。

2 背景知識

2.1 合數階雙線性群

設G和GT是階數為N的乘法循環群，其中，N=p*r，階N為2個不同素數p和r的乘積,g為G的生成元，映射e:G×G→GT滿足下列性質：

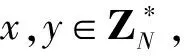
(2)非退化性：e(g,g)≠1。

(3)正交性：假設存在2個不同子群G1和G2的2個元素g1和g2，即g1∈G1，g2∈G2，則有e(g1,g2)=1，子群元素彼此正交。

2.2 安全模型

THH-CP-ABE方案的安全性證明是通過敵手A*同挑戰者C*之間的互動游戲模型給出的，詳細描述如下：

(1)初始化建立階段：敵手A*挑選并發送給挑戰者C*一個挑戰訪問結構。C*運行參數初始化算法，得到主密鑰MK和公鑰PK。C*保留主密鑰MK并將PK發送給A*。

(2)第1階段：敵手A*向挑戰者C*發出屬性集L={v1,v2,…,vn}的私鑰輸出問詢。C*通過運行私鑰生成算法生成私鑰SK并發送給A*。

(3)挑戰階段：敵手A*遞交長度一致的2個明文M1和M2給挑戰者C*。C*隨機選擇Mγ，γ∈{1,2}，運行明文加密算法，得到密文Cγ，并發送給A*。

(4)第2階段：敵手A*多次進行第1階段的操作，繼續私鑰輸出問詢。

(5)猜測階段：敵手A*猜測并給出γ′∈{1,2}。

如若在任意多項式時間內，敵手A*沒有以不可忽視的攻擊優勢將選擇明文攻擊不可區分性IND-CPA(INDistinguishability under Chosen-Plaintext Attack)游戲贏下，則該方案被認為是選擇明文(CPA)安全的。其中，攻擊成功的優勢為Adv=|Pr[γ′=γ]-1/2|。

3 本文方案

3.1 方案描述

本文提出的基于樹訪問結構的可隱藏策略且可追責私鑰的層次屬性加密方案(THH-CP-ABE)包括如下6個算法：

(1)Setup(1k)→(PK,MK)：輸入方案安全參數k，進行初始化運算，輸出公鑰PK和主密鑰MK。

(2)KeyGen(MK,L)→(SKTA)：輸入主密鑰MK、頂級權威的屬性集L，輸出頂級屬性權威的私鑰SKTA。

(3)Delegate(SKTA,L′,PK,MK,ID)→(SKU,Τ)：輸入頂級屬性權威的私鑰SKTA、公鑰PK、主密鑰MK及次級新成員的屬性集L′∈L，輸出新成員的私鑰SKU和查詢表T。

(4)Encrypt(m,Λ,PK)→(CT)：輸入需要加密的明文m、訪問結構Λ及公鑰PK，將訪問結構Λ按轉換規則轉換為訪問樹分派秘密s，輸出m的密文CT。

(5)Decrypt(CT,SKU,PK)→(mor ⊥)：輸入公鑰PK、包含用戶屬性集L′的用戶私鑰SKU和在訪問結構Λ下加密生成的密文CT，屬性集L′只有滿足訪問結構Λ要求時，方能計算并輸出明文m，否則輸出中止符號⊥，表示解密失敗。

(6)Trace(PK,T,SKU)→(IDor ⊥*)：輸入公鑰PK、查詢表T和私鑰SKU。若SKU檢驗通過，輸出用戶ID；否則輸出中止符號⊥*，表示不用追蹤。

3.2 方案模型

圖1為具有2級授權THH-CP-ABE方案的模型，由5個實體組成: 根權威、屬性權威、數據擁有者、云服務提供商和用戶(數據使用者)。根權威生成主密鑰和公鑰，為屬性權威頒發私鑰，擁有最高的權限，可以認為是完全信任的；各級屬性權威為新加入的次級屬性權威、數據使用者或者數據擁有者頒發私鑰；數據擁有者依照選取的訪問結構，將隱私文件加密成密文，并上傳到云端。用戶若想訪問此文件，當且僅當其屬性集滿足訪問結構要求，才能從云端下載文件后用解密算法對密文進行解密，從而實現隱匿策略的屬性加密細粒度訪問控制。云服務商提供密文上傳、存儲和下載的服務，同時可以追責泄露私鑰的違規用戶。方案采用層次授權體系，有效分散授權私鑰的計算量，避免根權威的負擔過重和風險過高，提升了安全性和效率。

THH-CP-ABE方案進行如下安全性假設：(1)假設云服務提供商會切實有效地履行用戶的上傳或下載請求，但同時存在好奇心，串通惡意用戶對隱私文件進行窺視或竊取，是半可信的；(2)假設數據使用者只能用只讀方式訪問隱私文件；(3)假設每個實體之間所有通信信道風險極低，都是安全可靠的。

3.3 方案構造

(1)Setup(1k)。

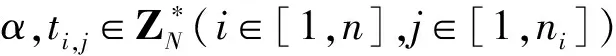
(2)KeyGen(MK,L)。

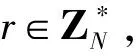
(3)Delegate(SKTA,L′,PK,MK,ID)。

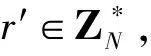
(4)Encrypt(m,Λ,PK)。

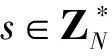
①若節點標識符是∧(與操作)，使用(t,n)Shamir秘密共享方案來共享秘密s，n是孩子節點的個數，門限值t=n。向所有孩子節點依次分派si=f(i)并標注為已分派。

②若節點標識符是∨(或操作)，t=0，向所有孩子節點依次分派s并標注為已分派。

③若節點標識符是of(門限操作)，且使用(t,n)Shamir秘密共享方案來共享秘密s，t是用來重構秘密s的孩子節點數。向所有孩子節點依次分派si=f(i)并標注為已分派。

密文由樹中葉子節點的值組成，i表示葉子節點的位置索引，t表示孩子節點個數，aj表示從U中隨機取出的屬性。

(5)Decrypt(CT,SKU,PK)。

計算檢驗函數的值F，若F=(L′?Λ)=0，返回⊥。若F=(L′?Λ)=1，計算明文m′：

其中，li(0)是樹索引i計算出來的拉格朗日系數。輸出明文m′。

(6)Trace(PK,T,SKU)。

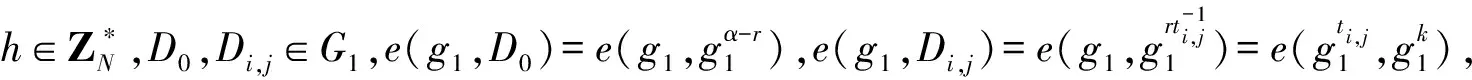
4 方案分析

4.1 正確性證明

執行解密算法Decrypt()階段，數據使用者獲得密文CT后，唯有數據使用者自身的屬性集L′滿足了訪問結構Λ的要求，才能用解密算法對密文進行解密，本文方案的正確性證明如下所示：

由于合數階雙線性群的正交性原理，THH-CP-ABE方案在加密算法中引入合數階子群中的隨機元素R′0和R′j，將訪問結構隱形嵌入在密文中實現策略隱匿。從上述的正確性證明中可以看出，解密結果的正確性不受隨機元素影響，能有效地防止敵手通過訪問結構中的信息推斷出用戶隱私。

4.2 安全性證明

假設敵手A*能用不可忽視的優勢ε/2勝得IND-CPA游戲打破本文方案，則存在挑戰者C*可用優勢ε/2解決DBDH假設。具體證明過程如下：

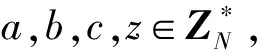
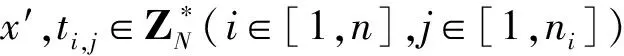
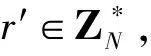
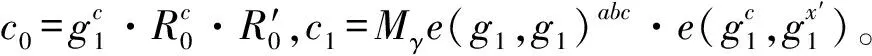
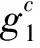
①若節點標識符是∧，f(i)的階數設為n-1，n是葉子節點的總數。

②若節點標識符是∨，f(i)的階數設為0，f(0)=c。

③若節點標識符是of，f(i)的階數設為t-1，t是可恢復秘密的葉子節點的總數。

(5)第2階段：多次進行第1階段私鑰輸出問詢。

(6)猜測階段：敵手A*對γ′進行猜測,γ′∈{1,2}，有以下2種情況：

①若γ′=γ，說明敵手A*能猜想Z=e(g1,g1)abc，挑戰者C*能獲得有效密文，其優勢為Pr[γ′=γ|Z=e(g1,g1)abc]=1/2+ε。

②若γ′≠γ，說明敵手A*能猜想Z=e(g1,g1)θ，只能獲得隨機密文，無法獲得有效密文，挑戰者C*的優勢為Pr[γ′≠γ|Z=e(g1,g1)θ]=1/2。

因此，挑戰者C*可以解決DBDH假設，其解決優勢為ε/2。THH-CP-ABE方案在此安全模型中是安全的。

4.3 效率分析

本節將比對THH-CP-ABE方案與其他屬性加密方案，以說明THH-CP-ABE方案的優勢。

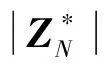
從表1中可以看出，本文方案與文獻[6,12]方案相比較，主密鑰和密文長度會更短，本文方案與文獻[6]方案的公鑰長度一樣長，但比文獻[12]方案的公鑰長度稍短。本文方案的構造是基于合數階群，私鑰長度會稍長，但提高了安全性，同時引入層次化授權結構，提高了分發私鑰的授權中心的效率。一般情況下，|u|和|E|小于n，且在復雜的方案中，下級用戶個數和訪問結構中屬性數量越多，|u|、|E|和n的差會越大，因此本文方案的通信和存儲代價更小，更便于傳輸和私鑰保存。

從表2中可以看出，本文方案的加密和解密計算開銷都比文獻[6]方案的更優，同時本文方案還支持密鑰追責。對比文獻[12]方案，參與加密屬性數量較少時，本文方案加密計算開銷略高，在屬性數量增多后，本文方案體現出加密優勢，在解密開銷方面也小于文獻[12]方案的。文獻[16]方案同樣可以使訪問策略隱匿，但在解密中，比本文方案增加了|L|+1次雙線性對運算，加密中群G上的運算次數也有所增加。文獻[5]方案也是基于訪問樹提出的，與本文方案一樣，同樣支持策略隱匿和層次加密。在解密開銷方面，本文方案的雙線性對運算次數減少了|L|+1次，在加密開銷方面，本文方案則遠遠優于文獻[5]方案。

Table 1 Keys and ciphertext length comparison of different schemes

Table 2 Characteristic and time cost comparison of different schemes

為了更精準地評估本文方案的運行效率，通過實驗對本文方案和文獻[6,12]的方案進行計算開銷仿真測試比對。仿真測試的PC機配置3.30 GHz的Intel Core i5-4590 CPU與8 GB RAM，使用Java的JPBC密碼庫。圖2和圖3分別表示THH-CP-ABE方案與2種對比方案在不同數量屬性參與的加密和解密過程的時間消耗對比。

從圖2可以看出，隨著屬性數量的增加，文獻[6,12]方案的加密開銷隨之線性上升，本文方案在參與加密的屬性數量為5～20個時，加密開銷略高于對比方案，隨著屬性數量|E|增加，本文方案將具有明顯優勢。

從圖3中能看出，本文方案和對比方案的解密計算開銷均隨參與解密的屬性數量的增加而線性變化，本文方案解密開銷略低于文獻[12]方案的解密開銷，明顯低于文獻[6]方案的解密開銷。

5 結束語

本文在合數階雙線性群下基于樹訪問結構，提出了一種可隱匿策略且可追責私鑰的層次屬性加密方案THH-CP-ABE。THH-CP-ABE方案使用層次授權體系，減少了根權威的負荷和風險；采用樹訪問結構，使訪問策略具有高表達力和高拓展性；運用合數階群的正交性原理，將合數階子群的隨機元素加進密鑰生成算法中，實現了隱匿訪問策略；通過用戶標識能夠及時有效地追責違規泄露私鑰的用戶。實驗結果和效率分析顯示，THH-CP-ABE方案在加解密效率上優于對比方案，且在功能上更豐富。后續研究方向是在現有方案中加入在線離線加密和屬性撤銷支持，使方案能更高效、更安全地運用。