考慮相依邊負載的相依網絡魯棒性研究

余榮斌，蔣 沅，嚴玉為，洪 成

(南昌航空大學信息工程學院 南昌 330063)

在現實世界中，存在著許多相互依賴的復雜網絡，這些不同網絡之間存在著緊密聯系。當網絡受到某些因素影響時，會對其他相關網絡產生不同程度的危害，進而造成大規模損失。如2019 年3 月委內瑞拉電力系統遭遇多次攻擊[1]，國內大部分地區持續停電，電網故障導致交通堵塞、信息網絡受阻；2020 年新冠肺炎疫情在全球爆發[2]，造成大規模傳播，社會各個行業都受到嚴重影響；2021年3 月“長賜”號在蘇伊士運河擱淺[3]，導致全球海運航道發生堵塞，對一些大宗商品市場、全球供應鏈和原材料價格帶來了一系列影響。因此，研究此類相依網絡之間的聯系和魯棒性具有重要的現實意義。

自2010 年，文獻[4]在《Nature》雜志上發表后，相依網絡的應用與研究成為了國內外學者關注的熱點。目前，相依網絡失效模型在一系列基礎設施網絡中應用較為廣泛，如文獻[5]分析了在極端天氣下，公交?地鐵復雜雙層網絡的連鎖故障和網絡系統的脆弱性演化。文獻[6]基于出行時間的可達性、出發的最佳可及性和往返行程的無障礙性3 種衡量行程時間的指標，來分析時變可訪問性對地鐵和高鐵相依網絡系統的影響。文獻[7]先對電力信息物理相依系統進行建模，后深入分析了節點脆弱性新特性、線路耦合深度和信息失效對網絡相變特性的影響。文獻[8]構建了高鐵?普鐵交通雙層復雜網絡，并對子網絡和相依網絡的拓撲靜態指標進行了分析。而文獻[9-10]分別在隨機攻擊和蓄意攻擊的基礎上，提出了一種考慮破壞力隨距離衰減的局部攻擊模式和多種攻擊方式組合下的聯合攻擊策略。文獻[11-12]分別提出局部優化NPC(鄰居節點優先連接)的耦合策略和基于重疊鏈路結構的相互依賴網絡耦合策略，這些耦合策略相較于傳統的隨機、同配和異配耦合模式能更有效地增強網絡系統的魯棒性。文獻[13]在滲流理論的基礎上提出了級聯故障滲流模型，并分析了相依網絡的耦合強度對網絡相變特性的影響。文獻[14-15]基于負載局域分配原則提出了負載級聯失效模型，引入了節點負荷過載的失效情況，并研究了具有不同攻擊策略、連接模式和負載分配機制的相互依賴網絡的魯棒性。文獻[16]提出一種新的基于社區結構的容量分配策略，在不改變網絡結構的情況下，這種策略能有效減少級聯故障，提高網絡魯棒性。文獻[17]提出了一個基于負載波動下相互流量重新分配的依賴網絡級聯失效模型，并通過流量損失參數來分析網絡現有資源的流量損耗。但這些研究的負載級聯失效模型集中于分析網絡內的節點和連邊，忽視了網絡間的相依邊同樣具有負荷流動的現象。文獻[18]通過建立對稱相依網絡和不對稱相依網絡模型，對負載最大的子網絡相連邊和相依邊分別進行失效，對比網絡相連邊和相依邊對相依網絡臨界成本的貢獻，然而文獻中并未考慮現實相依網絡中相連邊和相依邊負載所指代的物理意義并不相同，網絡內的負載在進行負載重分配時一般不進行跨網絡傳輸。

通過對上述文獻的梳理，發現多數文獻的研究并沒有考慮子網絡之間相依邊的負載，現實中不但網絡內部存在負載，而且不同網絡之間的信息傳遞也具有負荷流動的現象。相依網絡中的相依邊不但具備邏輯上的相依關系，也存在功能上的實際負載量。如電力網絡與交通網絡之間存在具體信息的傳遞，這些信息也受負荷流動和容量限制的約束；在不同的交通網絡間存在換乘問題，公交網絡站臺和地鐵網絡站點之間的換乘路線可視作網絡間的相依邊，換乘的人數為相依邊上的負載量，而惡劣天氣造成的部分路面積水和道路維修導致的局部封路等情況都會使乘客換乘不便，不得不改換鄰近站點進行換乘。

本文在這些研究的基礎上，提出了考慮相依邊負載的相依網絡級聯失效模型，并定義相依邊的初始負載和初始容量，失效情況綜合考慮了相依邊過載失效、相依節點故障和非最大連通子圖損失。以2021 年6 月南昌地鐵網絡(http://www.ncmtr.com)和部分公交網絡(https://nanchang.8684.cn)組成的相依網絡作為模型的實際用例，對模型的物理意義和合理性進一步說明。另外本文對考慮相依邊負載的相依網絡進行了多角度的分析，為進一步改善相依網絡的級聯失效提供新的途徑。

1 考慮相依邊負載的相依網絡級聯失效模型

1.1 相依網絡拓撲結構與性質分析

本文的相依網絡系統由獨立的兩個子網絡構成，分別為子網絡GA和 子網絡GB，而且節點總數為N=NA+NB，它們都有特定的網絡拓撲結構，并通過一定的方式進行連接。其中子網絡中內部節點連接的邊定義為相連邊，子網絡GA和GB之間節點連接的邊定義為相依邊。

網絡系統中的子網絡以GA網絡為例，它的簡單系統圖可以表示為GA=[VA,EA]， 其中VA={vAi|i=1,2,···,NA}表 示相依網絡中子網絡GA的節點集，EA={eAij|eAij=(vAi,vAj),i=1,2,···,NA;j=1,2,···,NA;i代 表了子網絡GA中節點之間相連邊的邊集，eAij表示子網絡GA中 節點vAi與節點vAj相連，同理子網絡GB也具有相類似的系統圖表示。

在相依網絡中將相依邊的邊集定義為EAB={eAiBj|eAiBj=(vAi,vBj),i=1,2,···,NA;j=1,2,···,NB;i和j可以相等}，當eAiBj=1表 示子網絡GA中的節點vAi與子網絡GB中 的節點vBj連接，即子網絡GA中節點vAi與子網絡GB中 節點vBj具有相依關系，反之則eAiBj=0。

為方便研究相依邊的負載分配，本文定義一個新的參數：鄰近相依邊集，某相依邊eAiBj的鄰近相依邊集可表示為E L=ELA∪ELB， 其中ELA={eAiBb=(vAi,vBb)|vBb∈Γi}， ELB={eAaBj=(vAa,vBj)|vAa∈Γj}，Γi表示子網絡GB中 除節點vBj以外與節點vAi相連的節點集合， Γj表示子網絡GA中 除節點vAi以外與節點vBj相連的節點集合， Γi和 Γj為點集。鄰近相依邊集如圖1 所示，設某相依邊為eAiBj，那么它的鄰近相依 邊 集 EL 有eAa1Bj、eAiBb1和eAiBb2。上 式 中Γi={vBb1,vBb2}， Γj={vAa1}， ELA={eAiBb1,eAiBb2} ， ELB={eAa1Bj}， EL=ELA∪ELB={eAa1Bj,eAiBb1,eAiBb2}。

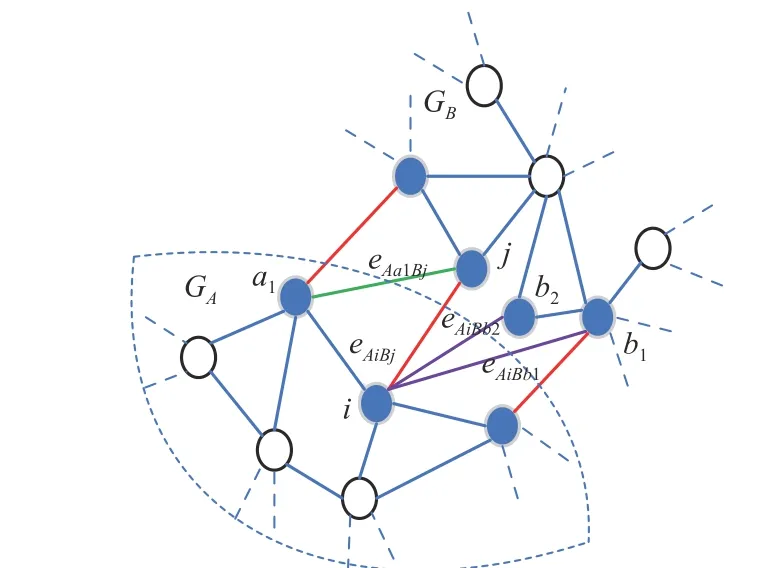
圖1 相依網絡的鄰近相依邊集

為進一步分析文中所提出的考慮相依邊負載的相依網絡的相依程度和耦合模式，沿用文獻[19]定義的兩個參數F和K，F為相依節點的比例，K為相依冗余度。FA表 示子網絡GA的相依節點數占子網絡GA節 點總數的比例，FB表示子網絡GB的相依節點數占子網絡GB節 點總數的比例；而KA為在子網絡GA中 相依節點的平均相依邊數，KB為在子網絡GB中相依節點的平均相依邊數。本文定義相依網絡為對稱相依網絡時，NA=NB，F=FA=FB，即兩個子網絡具有相同的網絡規模和相依節點比例，且K=KA=KB；若為不對稱相依網絡時，即NANB，FAFB時 ，此時K=min{KA,KB}。如在圖2中，FA=1，FB=0.6，KA=KB=3。

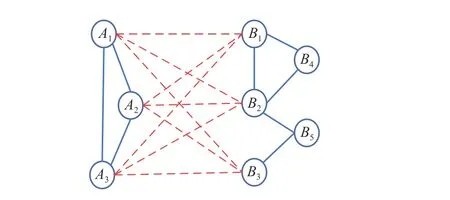
圖2 兩個簡易子網絡構成的相依網絡

同時網絡之間的耦合關系以節點的度值為標準，子網絡GA與GB之間有同配耦合、異配耦合和隨機耦合3 種不同的耦合模式。其中同配耦合是先對子網絡GA與 子網絡GB中的節點分別按節點度值的降序排列，再將節點進行配對連接，連接的具體步驟為先將每個子網絡中降序排列好的前M個節點進行分組(當NA=NB時 ，M=NA=NB； 當NANB時，M=min{NA,NB}) ，以K個節點為一個單元組(其中K為相依網絡的相依冗余度，當M個節點無法被相依冗余度K整除時，則剩余的余數單獨組成最后一組)。假設子網絡GA和GB中 前M個節點被分為n組 ：Z1,Z2,···,Zn和U1,U2,···,Un， 將子網絡GA中第一組的每個節點與子網絡GB中第一組的所有節點進行連接，即Z1?U1， 并以此類推使得Zi?Ui，最終Zn?Un。 同理可知，異配耦合則將子網絡GB中的節點按度值的升序排列，將子網絡GA中的節點按度值降序排列，具體連接方式與同配一致；隨機耦合則對每個子網絡隨機選取M個節點進行分組，具體連接方式與異配相同。

在子網絡的選取時，本文采用3 種經典的人工網絡模型作為相依網絡的子網絡。其中BA(Barabási-Albert)無標度網絡模型的具體構建算法是先在給定初始節點m0的情況下，每一步都添加一個新的節點，然后將新節點與m個已存在的節點進行相連，且規定m?m0，相連方式按擇優連接的概率進行連接[20]。WS(Watts-Strogatz)小世界網絡模型的構造算法是先從規則網絡開始，再進行隨機化重連，即將網絡中的每條邊以概率p進行重連[21]。ER(Erd?s-Rényi)網絡模型構建方法是以WS 網絡模型為基礎的，不同點在于重新布線的概率p=1[22]。本文中這3 種經典網絡的節點數都選擇200 個節點。

將2021 年6 月南昌地鐵與部分公交網絡系統作為模型的應用實例，地鐵公交網絡是由3 條地鐵線路與40 條客流量最大的市區公交線路組成。由3 條地鐵線路組成的地鐵網絡共有70 個站點，而由40 條市區公交線路組成的公交網絡共有511 個公交站點。將站點抽象為網絡節點，相同交通工具的站點間的連接線路看作相連邊，不同交通工具站點之間可換乘的線路為相依邊，可換乘的條件設為地鐵站點和公交站點之間距離在800 m 以內，換乘的人數抽象為相依邊的負載。若在換乘時遇到不可避免的因素，乘客不得不改換鄰近站點進行換乘，如何優化分配改換站點的人數以使得換乘線路不會因為換乘人數太多而導致擁堵和滯留，這一問題可看作考慮相依邊負載的相依網絡級聯失效模型的實際應用之一。將市區公交網絡設為子網絡GA，地鐵網絡為子網絡GB，此相依網絡的相關參數如表1所示。

表1 2021 年6 月南昌地鐵與部分公交網絡的相關參數

1.2 相依邊負載容量模型

在ML 模型的基礎上[23]，本文提出了一種考慮相依邊的負載容量模型，相依邊eAiBj的初始負載表示為：

式中， α為可調參數，一般 α ?0，表示相依邊的冗余程度即容忍系數，控制相依邊的容量閾值。

基于相依邊的負載重分配規則，假設相依邊eAiBj失 效時，鄰近相依邊eAxBy以一定的分配比例獲得額外的負載 ?LAiBj， 當LAxBy+?LAiBj>CAxBy時，鄰近相依邊eAxBy過載失效，網絡繼續對失效的相依邊進行負載分配，直到任意相依邊的容量大于負載時，網絡間相依邊的負載失效才停止。相依邊的負載重分配示意圖如圖3 所示。

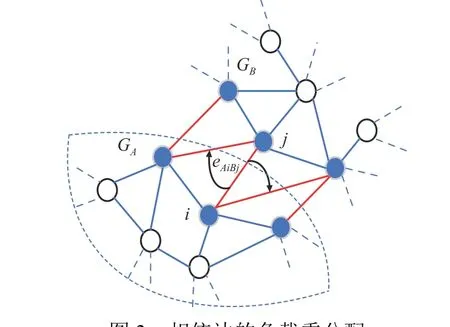
圖3 相依邊的負載重分配

1.3 級聯失效模型的構建

本文的級聯失效模型中失效具體情況一般分為以下4 種，并且任意一種攻擊和故障導致的節點失效，其對應的所有邊也會被清除：

1) 在初始狀態下外部攻擊導致的初始失效可分為3 種，其中任意一種攻擊方式都可以引發網絡的初始失效。

① 外部直接攻擊節點導致的節點失效。

② 外界進攻網絡內的相連邊，以至于節點失去所有相連邊，則該節點故障并被移除。

③ 外部襲擊網絡間的相依邊，致使相依節點失去所有相依邊，此相依節點失去了所有與另一個子網絡耦合鏈接的物理通道，相對應的信息或負荷無法通過該相依節點進行跨網絡傳輸，故視該節點失效。

2) 基于滲流理論的級聯故障滲流模型[19]，在子網絡中若某一節點脫離了最大連通子圖，則該節點失效[24]。

3) 在級聯失效過程中，若節點為相依節點，由于失去了所有的相依邊，該相依節點與另一個子網絡的依存關系消失，相依節點與另一子網絡間的正常聯系中斷，此相依節點失效[25]。

4) 基于上文中的相依邊負載容量模型，當網絡間的相依邊失效時，會將失效相依邊上的負載以一定比例分配給鄰近相依邊，若負載超過容量則發生過載失效，繼續導致鄰近相依邊集的故障。在地鐵公交網絡中，假設在理想狀態下換乘線路上的換乘人數超出額定的容量時，換乘線路失去基本換乘功能。根據以上4 種失效模式，制定了模擬考慮相依邊負載的級聯失效模型的詳細步驟如下。

① 對子網絡GA進 行初始攻擊，移除被攻擊的節點與連邊。

② 子網絡GA分 裂成若干個子圖和孤立節點。基于滲流理論，當節點移除比例超過臨界相變點，子網絡被分解成多塊互相不連通的集團。在網絡中只有最大連通片保持基本的功能和相對的全局連通性，由于其余子圖中的節點和孤立節點在結構上與最大連通子圖并不連通，故可視為故障節點[4]。

③ 子網絡GA內節點的移除，導致大量相依邊失效。根據相依邊負載容量模型，失效的相依邊對鄰近相依邊集分配額外的負載，當鄰近相依邊的總負載量超過容量限制時會導致過載失效。

④ 相依邊的過載失效和子網絡GA內節點的移除使得子網絡GB內相依節點失去大量的相依邊，子網絡GA的故障經過相依邊負載重分配后傳播到子網絡GB。 在子網絡GB中，那些失去所有相依邊的節點失效。

⑤ 基于級聯故障滲流模型，子網絡GB內發生步驟②中相似的非最大連通子圖失效。若此時整個系統達到穩定狀態，則失效結束，反之則將故障傳播到子網絡GA繼續步驟⑥，如此反復迭代直到系統達到穩定。

⑥ 子網絡GB內的失效會同樣影響網絡間的相依邊，網絡間的相依邊會發生步驟③中的相依邊過載失效。

⑦ 相依邊的過載失效會使得大量相依邊被移除，進而導致子網絡GA發生相依失效，故障又傳播回子網絡GA。

⑧ 系統的故障經過相依邊的傳遞，再次回到子網絡GA中，重復步驟②～⑦，直到系統達到穩定。

圖4 展示了一個簡易相依網絡的級聯失效過程，在相依網絡的初始狀態(如階段1)下，先蓄意攻擊子網絡GA中 的節點A3， 則節點A3和它的連邊(包括相連邊和相依邊)都失效，節點A3的失效導致節點A4脫 離最大連通子圖，則節點A4發生非最大連通子圖失效。相依邊eA3B1的失效，使得相依邊發生負載重分配，若鄰近相依邊eA5B1獲得額外負載后其總負載超過容量，則發生過載失效，繼續進行負載分配。相依邊eA5B1的鄰近相依邊獲得額外負載，若相依邊的總負載小于容量，則停止負載分配。又因為子網絡GB中 節點B1的 相依邊都被刪除，節點B1失效被移除，并且節點B1的 移除導致節點B4和B7脫離最大連通子圖，故而同樣發生節點失效，這些失效節點對應的連邊也被移除。在階段1 中失效結束后，網絡的狀態如圖4b 所示，此時子網絡GA中節點A7的 所有相依節點失效，故而導致節點A7發生相依失效。此時系統中節點不再發生失效，相依網絡達到穩定而且整個系統的狀態如圖4c 所示。

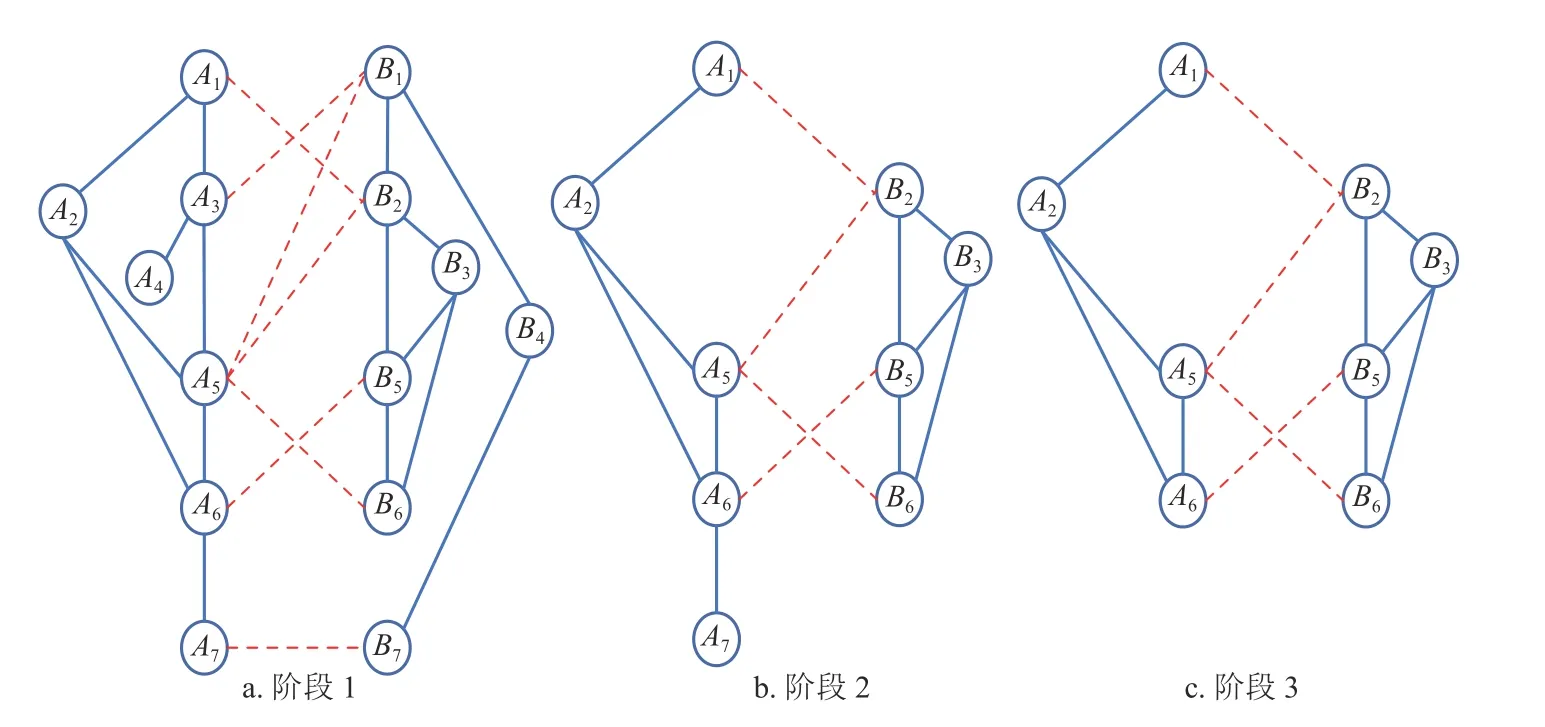
圖4 簡易相依網絡級聯失效的過程

1.4 網絡魯棒性測量指標

攻擊一定比例的節點后(若未特別說明，則是隨機攻擊子網絡GA的節點)，考慮相依邊負載的相依網絡模型會發生級聯失效。當網絡級聯失效達到穩定時，剩余最大連通子圖中有效節點數與初始狀態下子網絡的節點總數的比例為魯棒性指標，本文定義s為相依網絡的魯棒性測量指標，表示為：

式中，XA、XB分 別為子網絡GA和 子網絡GB中幸存最大連通子圖中的有效節點；NA、NB分別為子網絡GA和 子網絡GB中初始狀態下節點的總數。顯然s值越大，相依網絡的有效節點越多，整個網絡系統的魯棒性就越好。

為了避免隨機因素對整體仿真效果的影響，本文隨機仿真生成SM個相依網絡，并在相同的規則運行下得到一組魯棒性測量指標分別為s1,s2,···,sSM。對這組數據取均值S=(s1+s2+···+sSM)/SM。本文仿真均取SM=2 000。

2 數值分析

2.1 相依邊負載分配策略對網絡魯棒性的影響

在相依邊負載分配時，相依邊的負載重分配策略對網絡的抗毀性有一定程度的影響，本文采用4 種不同的負載重分配比例來對相依邊過載失效進行分析。

1) 平均分配策略。當相依邊eAiBj失效且存在鄰近相依邊時，將相依邊的負載平均分配給其所有鄰近相依邊。則相依邊eAiBj分 配給鄰近相依邊eAxBy的分配比例為：

式中，m表示子網絡GA中 節點vAi上的相依邊數；n表示子網絡GB中 節點vBj上的相依邊數。

2) 負載分配策略。由于負載反映了相依邊上實際信息量，故對所有鄰近相依邊負載進行歸一化，取其相對大小來作為分配比例。按失效相依邊的鄰近相依邊負載比例進行重新分配，相依邊eAiBj分配給鄰近相依邊eAxBy的比例為：

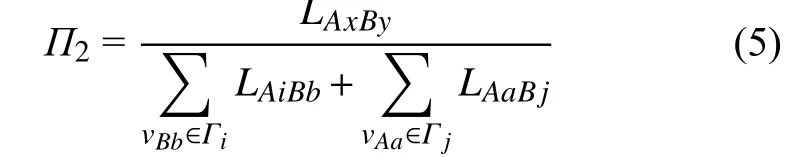
式中，LAxBy為 鄰近相依邊eAxBy的 負載； Γi表示子網絡GB中 除節點vBj以外與節點vAi相連的節點集合；Γj表示子網絡GA中 除節點vAi以外與節點vBj相連的節點集合。其中LAiBb為求和內容，即求和的通項，表示eAiBb的 負載，eAiBb=(vAi,vBb)，求和的取值范圍為vBb∈Γi，同理LAaBj具有類似意義。

3) 剩余容量分配策略。在級聯失效的過程中，相依邊所剩余的容量與其剩余可承受的負載成正比。所以相依邊eAiBj分 配給鄰近相依邊eAxBy的比例為：

式中，LAxBy為 鄰近相依邊eAxBy的 負載；CAxBy為鄰近相依邊eAxBy的 容量； Γi表示子網絡GB中除節點vBj以外與節點vAi相連的節點集合； Γj表示子網絡GA中 除節點vAi以外與節點vBj相連的節點集合。

4) 混合分配策略。將以上幾種不同的重分配策略進行加權組合，則可得到混合分配策略。定義加權參數w1,w2,w3且w1+w2+w3=1，則分配比例為：

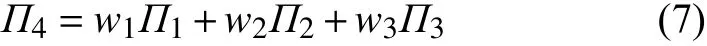
為研究相依邊負載分配策略對網絡魯棒性的影響，將3 種經典人工網絡作為相依網絡的子網絡，子網絡間采用隨機耦合。令子網絡的平均度= 2，相依節點比例F=1，相依冗余度K=4，容忍系數 α=0.5，同時將南昌地鐵和部分公交網絡作為實驗用例，探究不同的相依網絡負載重分配策略對系統的魯棒性影響，其仿真結果如圖5 所示。從圖5 可知，未考慮相依邊負載分配策略時，系統的魯棒性相對較好，因為此時系統僅考慮了拓撲結構對系統的影響，忽略了網絡具有負荷流動的功能性特征，在結構特性的基礎上考慮負載分配因素會增加網絡故障的風險，但這也更符合現實要求。而平均分配策略在所有分配策略中表現最糟，剩余容量分配策略效果最好，負載分配策略和混合分配策略下的系統魯棒性介于前兩者之間。這是由于平均分配策略忽略了相依邊的差異性，鄰近相依邊的剩余容量對接受額外負載的能力起很大作用。而剩余容量分配策略則是根據相依邊的相對剩余容量進行分配，從而降低了相依邊過載失效的風險。此外，混合分配策略不但考慮了相依邊的剩余容量，而且考慮了失效相依邊的鄰近相依邊總數，合理的對負載進行了分配。因此，混合分配策略相對較佳。另外南昌地鐵和部分公交網絡組成的相依網絡與BA 網絡組成的相依網絡仿真結果類似，整體下降的趨勢相似，因為地鐵和部分公交中網絡的平均度約為為1，網絡節點的度值分布較平均，而BA 網絡的節點度值分布較集中，所以BA 網絡組成的相依網絡下降速度較快。在攻擊比例為0 時，WS網絡組成的相依網絡和ER 網絡組成的相依網絡的魯棒性不為1，原因在于WS 網絡和ER 網絡的平均度 為2 時，WS 網絡和ER 網絡可能為不完全連通圖，存在若干個子圖。綜上所述，對相依邊負載進行合理的分配，能減小相依邊過載失效的故障率，提高網絡的魯棒性。

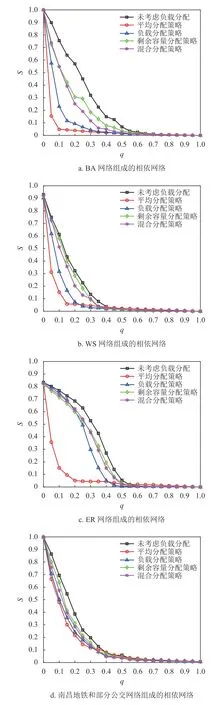
圖5 不同相依邊的負載分配策略下魯棒性的對比

2.2 網絡組合形式對相依網絡魯棒性的影響

為考察不同網絡組合對網絡魯棒性影響的差異性，設子網絡的平均度 =4，相依節點比例F=1，相依冗余度K=4，容忍系數α=0.5，子網絡之間隨機耦合，并且相依邊負載重分配采用負載分配策略，仿真分析相依網絡的平均幸存節點比例和攻擊節點比例的關系。仿真結果如圖6 所示。

從圖6 中可以看出，在考慮相依邊負載的相依網絡模型中，不同的組合網絡的平均幸存節點比例都隨著攻擊不斷下降，當破壞比例達到0.8 時，網絡系統完全坍塌；在 0 .2 ?q ?0.7時，網絡的組合形式對系統抗毀性的區別最明顯。WS-WS 網絡的下降速度在這些組合網絡中最慢，BA-BA 網絡的魯棒性最差，而ER-ER 網絡的抗毀性相對較好，混合網絡則介于兩者之間，并且混合相依網絡相較與單一網絡組成的依賴網絡差異性更小。通過對比分析，考慮相依邊負載的相依網絡模型在不同的組合方式下的魯棒性與文獻[26]的研究結論類似，混合網絡的魯棒性往往介于兩者之間，而本文考慮相依邊負載的相依網絡在WS-WS 網絡模式下抗毀性更加優異。

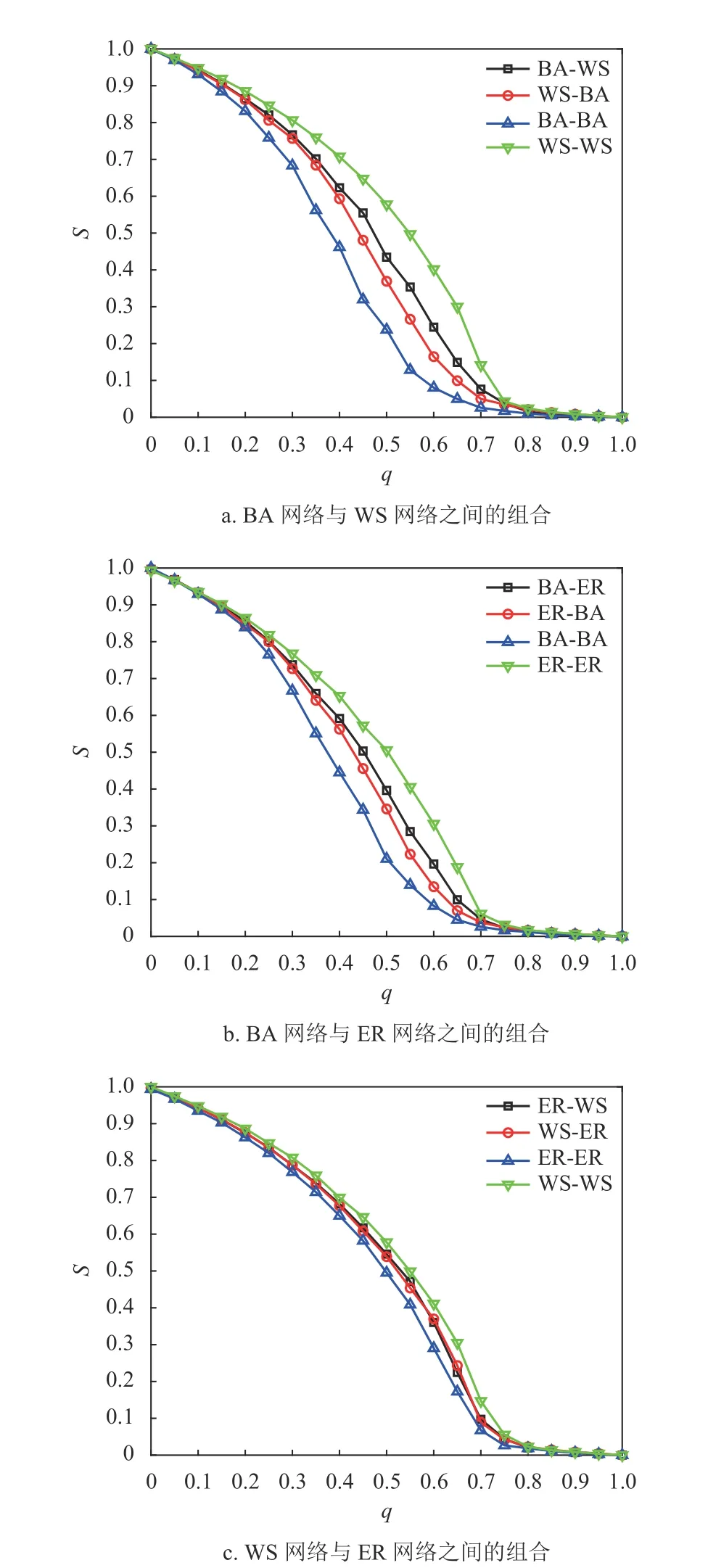
圖6 不同網絡組合下的相依網絡魯棒性的對比

2.3 子網絡的平均度對網絡魯棒性的影響

為分析子網絡的平均度對網絡魯棒性的影響，設容忍系數 α=0.8，兩個子網絡的模型為BA網絡，相依節點比例F=1，相依冗余度K=4，并用同配、異配和隨機耦合3 種不同的耦合方式分別進行連接，采用的相依邊負載重分配策略同上。仿真分析的結果如圖7 所示。

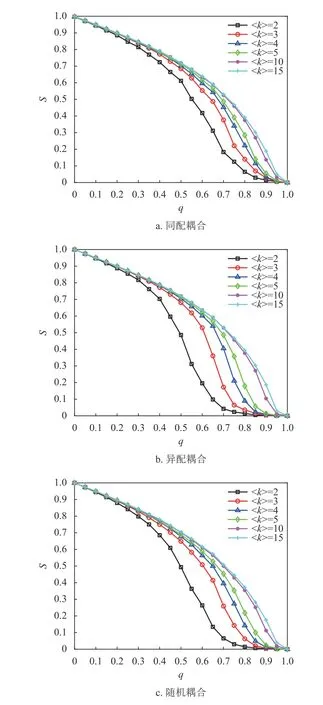
圖7 不同子網絡的平均度下的相依網絡魯棒性的對比

由圖7 可知，隨著子網絡的平均度 增大，網絡的魯棒性也隨之增加，同時當平均度>5 后，平均度對相依網絡魯棒性的強化有所減緩，而 ?10時，系統在同等破壞規模下幸存的有效節點比例差別并不明顯，這說明子網絡平均度對網絡抗毀性優化有較強的局限性，雖然提高網絡內節點的度值能有效地抵御非最大連通子圖失效，但節點度值對網絡整體失效的影響有一定限制。另外在 0 .4 ?q?0.7時，相依系統中幸存節點減少較快，不同平均度對網絡破壞程度的區別開始顯現；當q?0.7時系統的坍塌速率明顯增加。且無論哪種耦合方式，整體下降趨勢相同，而同配耦合下相依網絡的魯棒性最好。故此，提高子網絡的平均度能在一定程度上改善網絡系統的抗毀性。

2.4 網絡間的相依程度對相依系統魯棒性的影響

分析網絡間的相依程度對網絡系統的影響，兩個子網絡都為BA 無標度網絡，并以不同的耦合方式為研究對象，令子網絡的平均度 為4，容忍系數和相依邊負載重分配策略同上文一致。通過隨機攻擊子網絡GA中 的一定比例q的節點，同時調節相依節點比例與相依冗余度的相對大小來進行仿真實驗，仿真結果如圖8 和圖9 所示。

從圖8 可知，在3 種耦合模式下，網絡系統的魯棒性都隨著攻擊節點比例的增加而遞減。且當相依冗余度K為4 時，不同的相依節點比例對網絡系統魯棒性具有差異性。在攻擊比例q=0.4 時，不同的相依節點比例所導致的系統魯棒性差異性開始顯現，并隨著攻擊比例的增大，網絡系統魯棒性差異性越大。另外，相依節點比例越大，系統的魯棒性越差，這與文獻[19]中的結論相同，再次驗證了相依節點比例對相依網絡系統魯棒性的影響。而且本文中相依節點比例的增加，增加了網絡間信息溝通和傳輸的渠道，但這也利于相依邊過載失效和相依失效的發生。

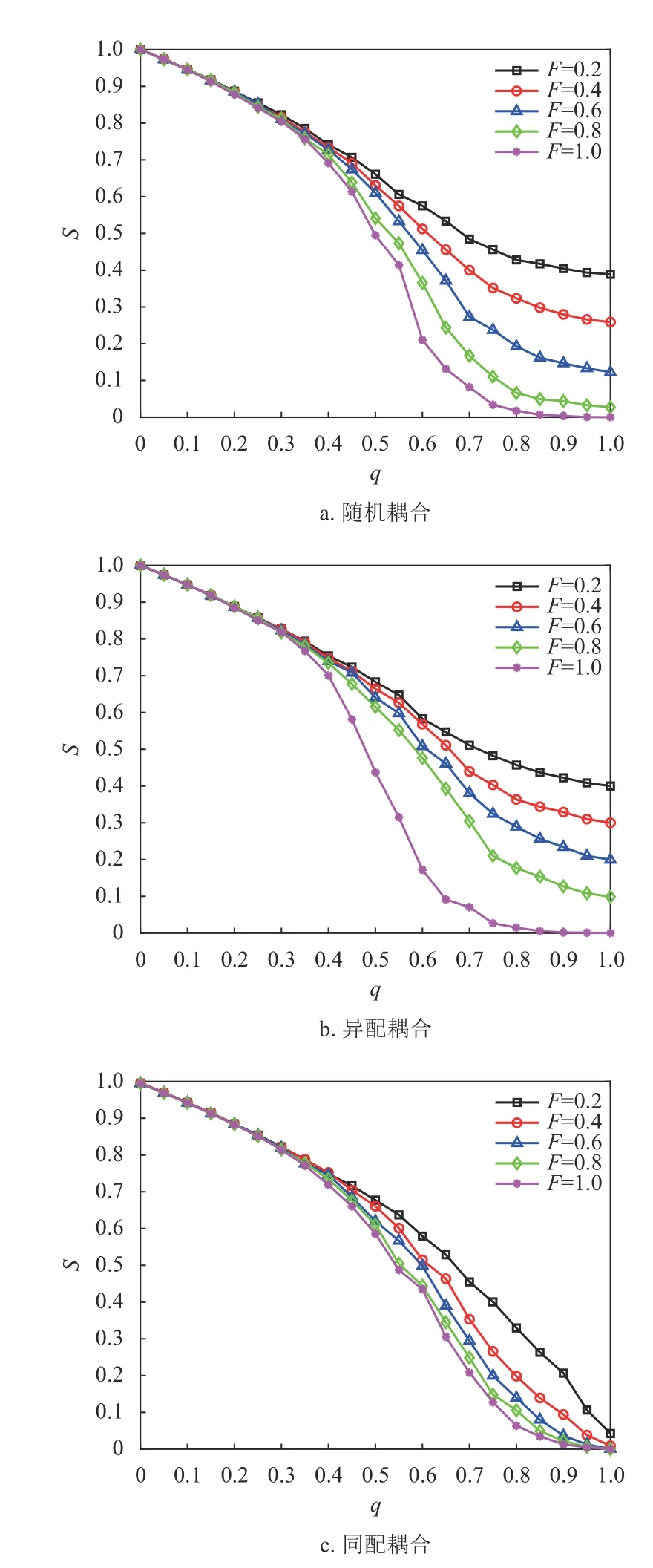
圖8 不同相依節點比例對相依網絡魯棒性對比

從圖9 可知，在F=1 下，相依冗余度對相依網絡系統的魯棒性影響較大。隨著相依冗余度的增加，相依網絡系統的魯棒性越強，即相依冗余度能有效地增強系統抵抗級聯失效的抗毀性，原因在于每個節點的相依邊數的增加有利于緩解相依失效和相依邊過載失效，并且單個相依節點增加相依邊也有助于分攤負載重分配時的額外負載，并減小相依失效的概率。此外隨著相依冗余度K的增加，K對相依網絡魯棒性的影響在逐步減小。這與文獻[19]中的結論相近，但本文考慮了相依邊的負載重分配，所以系統魯棒性的下降速率相較于文獻[19]更迅速，下降比例也更大。綜上所述，減少相依節點比例F，提高相依冗余度K能有效降低相依網絡的崩潰比例。

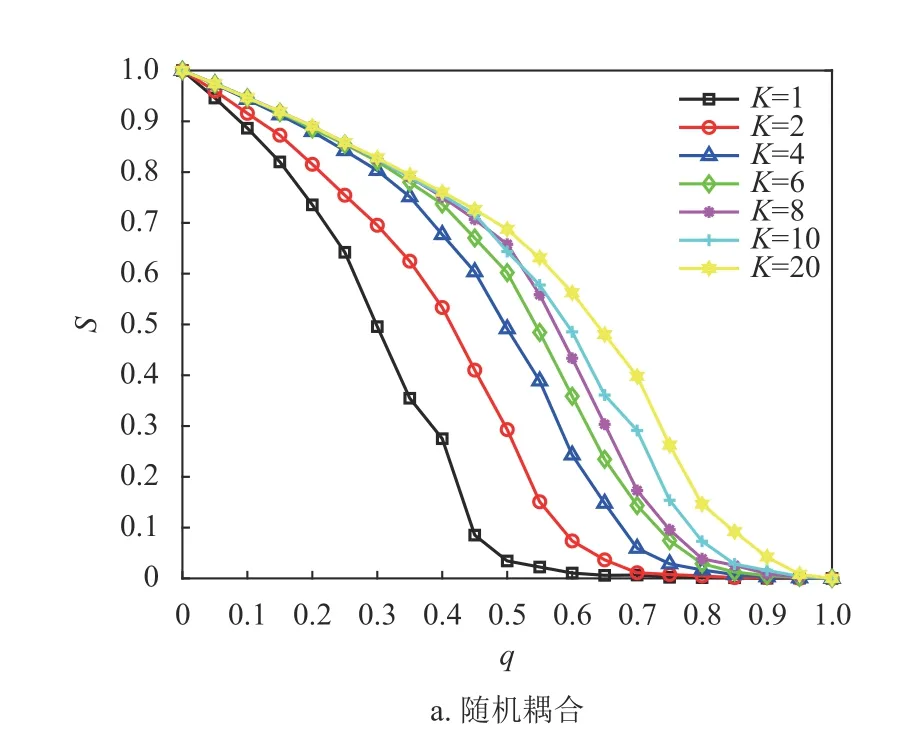
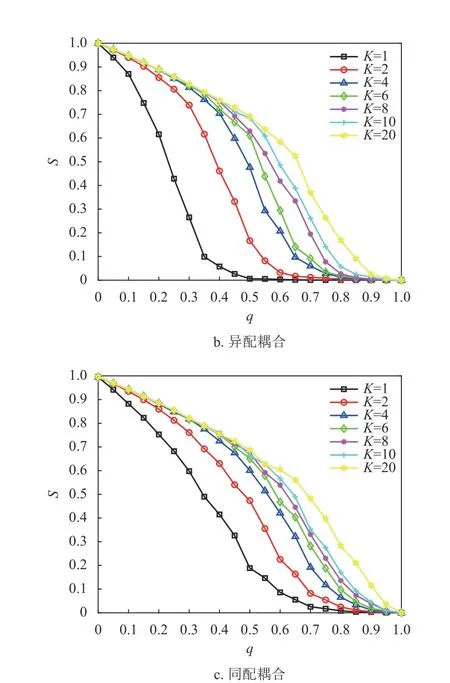
圖9 不同相依冗余度對相依網絡魯棒性對比

2.5 不同邊攻擊方式下相依網絡的魯棒性

本節在初始失效時分別攻擊一定比例的相連邊和相依邊，并通過系統處于穩定狀態時魯棒性指標的大小來判斷相連邊和相依邊對相依網絡的影響。在對系統進行蓄意攻擊時，先對相連邊進行加權處理，相連邊的權重為連接節點度值的乘積，即weij=ki×kj。初始狀態時將相連邊按權值降序排列，相依邊按初始負載的大小降序排列，取前面一定比例的邊進行攻擊。若子網絡中節點的相連邊或相依邊全都失效，則該節點失效。令系統的參數與負載重分配策略同上，子網絡模型選擇無標度網絡和地鐵公交網絡，并通過上文中3 種不同的耦合方式分別進行連接。在初始狀態下，采用不用的攻擊方式分別攻擊相連邊和相依邊，分析系統網絡的魯棒性。仿真結果如圖10 所示。

由圖10 可知，蓄意攻擊比隨機攻擊對相依網絡魯棒性的影響更大，蓄意攻擊相依邊時系統網絡的有效節點比例下降最快。因為攻擊負載較大的相依邊更容易導致相依邊的過載失效和相依失效。且無論網絡間的耦合采用何種方式，攻擊相依邊比攻擊相連邊對相依網絡的失效風險更高。另外相比于其他耦合方式，相依網絡在同配耦合下對于蓄意攻擊產生的故障效果最明顯，這是由于同配耦合時子網絡間度值較大的節點相連接，使得失效的傳播途徑和故障范圍更加廣泛。此外，對真實地鐵公交網絡的仿真結果，也同樣反映了相依邊對網絡系統的重要性，系統的整體下降趨勢與無標度相依網絡相似。相較于無標度網絡組成的相依系統，地鐵公交網絡的失效速率和故障比例更大，原因在于地鐵公交相依網絡的子網絡平均度和節點的相依冗余度較小，無法有效地抑制級聯失效的傳播。同時在地鐵公交網絡中子網絡的節點總數不相等，相依節點的比例FAFB，公交網絡中存在較多沒有相依邊的節點，這就使得在攻擊相依邊時，會幸存大量沒有相依邊的節點，所以在攻擊相依邊的比例達到100%時，系統依然存在一些幸存節點。

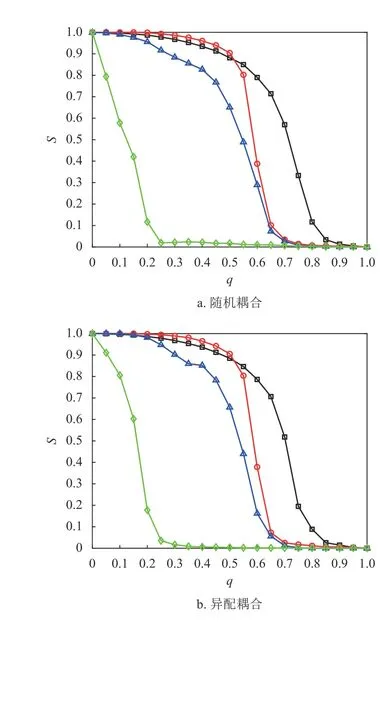
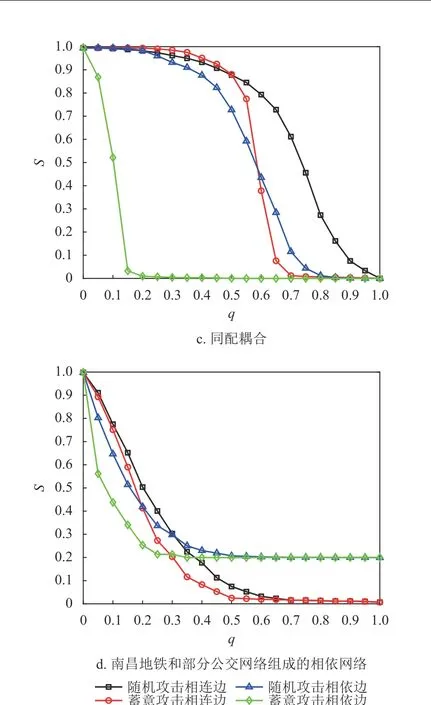
圖10 不同邊攻擊方式下相依網絡魯棒性對比

3 結 束 語

在現實中不同網絡之間信息或流量的傳遞與運輸往往具有明顯的負載效應，本文提出的考慮相依邊負載的相依網絡級聯失效模型綜合分析了此類現象。文中新定義了鄰近相依邊集，詳細解釋了相依邊失效時負載重分配的原則。并通過人工網絡和真實網絡對這一現象進行說明，考慮相依邊的負載會增加級聯失效的復雜性，但同時這也更符合實際網絡的故障狀態，并探討了耦合程度、子網絡平均度和攻擊方式等因素對考慮相依邊負載的相依網絡魯棒性的影響。仿真結果表明了增強網絡間的相互依賴比例會使得系統變得脆弱，但較大的相依冗余度能有效地遏制失效造成的破壞范圍；提高子網絡的平均度能顯著地抵御網絡內的非最大連通子圖失效；相較于相連邊，攻擊相依邊會加速整個網絡系統的坍塌。這些研究對優化相依網絡系統的魯棒性提供了參考，也對現實中不同網絡之間信息和流量的傳遞現象做出了一定的分析和解釋。然而，這些研究都是在無向網絡的基礎上進行的，考慮相依邊負載的級聯失效模型對有向網絡的影響有待進一步解決；此外，在對網絡系統進行級聯失效預防和恢復的過程中，文中所建立的失效模型如何增加恢復與預防的復雜性和困難程度是下一步研究的重點。