一類考慮垂直傳染、 接種及人均病床數的SIVS傳染病模型分析①
王琪, 竇霽虹
1.陜西工業職業技術學院, 陜西 咸陽 712000; 2.西北大學 數學學院, 西安 710127
經典的傳染病倉室模型通常根據疾病痊愈后是否具有免疫階段(即康復類倉室)分為不同研究方向[1-2], 而文獻[3]針對部分疫苗接種者具有暫時性免疫的實際情形, 在傳統無免疫階段的SIS模型基礎上加入了暫時性免疫倉室V, 并引發大量研究[4-7]. 通過分析發現在疫苗接種不完全有效時, 模型在一定條件下發生后向分支. 以乙型肝炎病毒為例, 首先其具有垂直傳染的特點; 其次, 可接種疫苗進行防治, 但5%~10%的人群會存在疫苗無應答現象, 即接種無效[8-9]; 同時疫苗在不同人群體內的存活時間不同[10], 除新生兒外的其他易感者均可在不同階段接種疫苗.
基于乙肝病毒的以上特點建立動力學模型, 并且考慮加入由文獻[11]定義的一個與病床數有關的飽和治療函數
其中:μ0,μ1分別是最小和最大恢復率. 通過研究分析系統發生鞍結點分支、 后向分支和Bogdanov-Takens分支的情況, 以此推斷包含病床數在內的有限醫療資源對傳染病控制的影響. 此后, 也有很多學者引用該治療函數進行研究[12-15], 以便更細致有效地研究與醫療資源有關的因素對傳染病防治的影響.
本文基于乙肝傳播特點建立一類考慮垂直傳染、 疫苗接種以及人均病床數量的SIVS模型, 同時對易感者以及易感者和接種者的新生兒預防接種. 通過對模型進行理論研究和數值分析, 總結出控制乙型肝炎疾病流的有效措施, 也可進一步為進行疫苗接種的傳染病防治提供了更豐富的理論基礎.
1 模型建立
本模型將某一地區的人口共分為3個倉室: 易感者、 染病者以及接種者. 假設此地區不發生人口遷移和因病死亡, 即環境總人口恒定, 則可直接假設S(t),I(t),V(t)分別表示在t時刻環境中易感者、 染病者和接種者的人口密度. 假設疾病的發生采用雙線性發生率. 由于不同階段人群染病概率不同, 則設m為易感者和接種者的新生兒疫苗接種比例;m′表示易感者的接種比例; 接種者與染病者接觸仍有一定染病概率, 這取決于疫苗的接種效率σ,σ∈(0, 1),σ取0代表疫苗完全有效, 取1 代表疫苗完全失效;q表示疾病的垂直傳染率;β表示染病者對易感者和接種者的感染率;b,d分別表示人口的出生率和自然死亡率, 假設人口的出生率與自然死亡率相等, 即b=d;μ為(1)式表示的治療函數;δ為人均病床數量, 可以衡量包括病床數在內的醫療資源情況;θ表示接種失效的比例. 該模型的傳播流程圖如下:
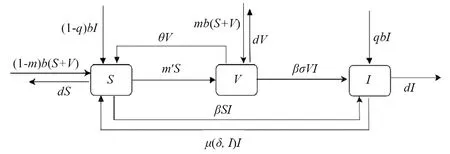
圖1 SIVS傳染病模型流程圖
根據傳播流程圖, 建立如下模型:
(1)
由于S=1-I-V, 將模型進行化簡降維后, 模型(1)可化為:
(2)
要使模型具有實際的生物學意義, 則在區域:
內考慮模型(2)的動力學性質.
2 主要結果
2.1 基本再生數
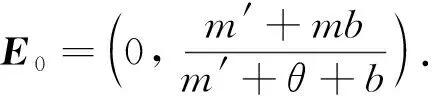
本節將采用第二代生成矩陣法計算疾病的基本再生數R0. 那么
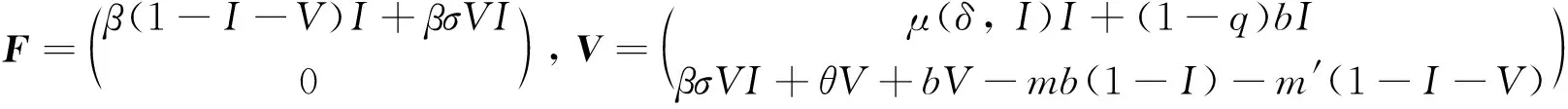
通過F,V在無病平衡點E0處的Jacobi矩陣得到基本再生數表達式:
(3)
注此處R0>0恒成立. 由于模型中參數均在(0, 1)范圍內, 則有b>(1-σ)mb.
2.2 平衡點存在性
H(I)=β2σI3+h1I2+h2I+h3=0
(4)
其中:
由于三次方程的根較為復雜, 將利用幾何學的方法對其進行證明.
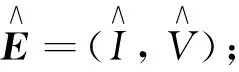
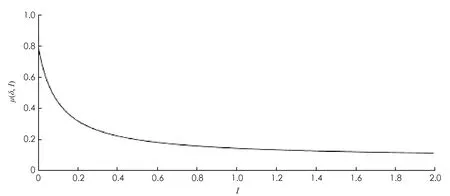
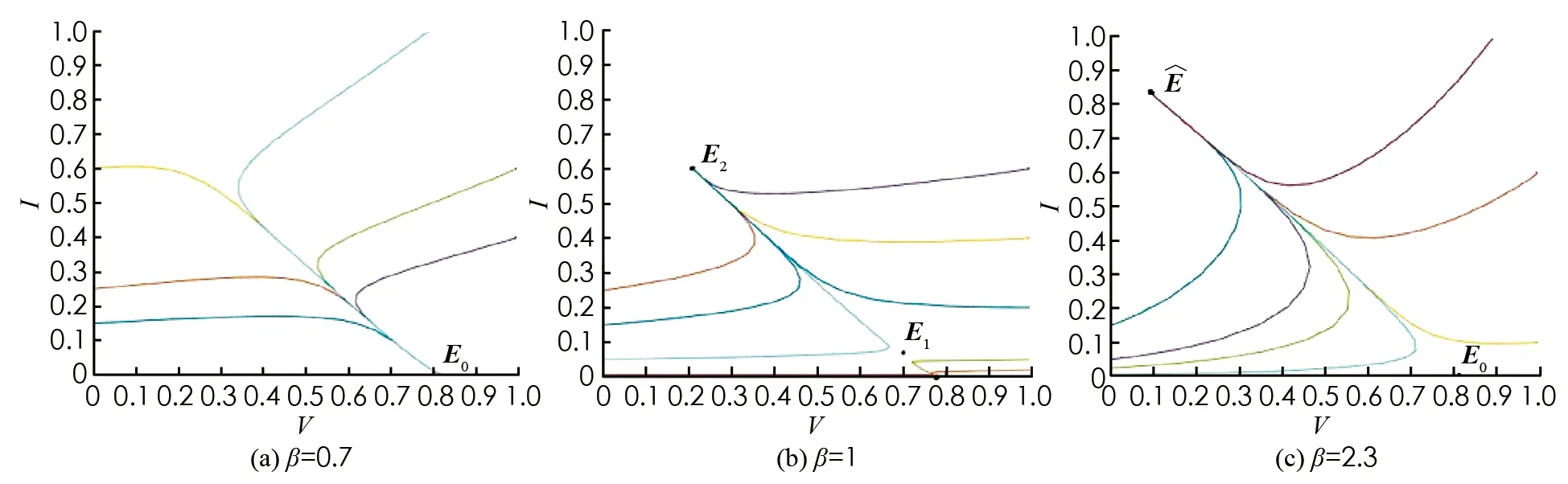
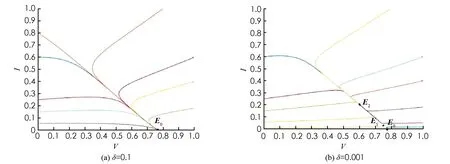
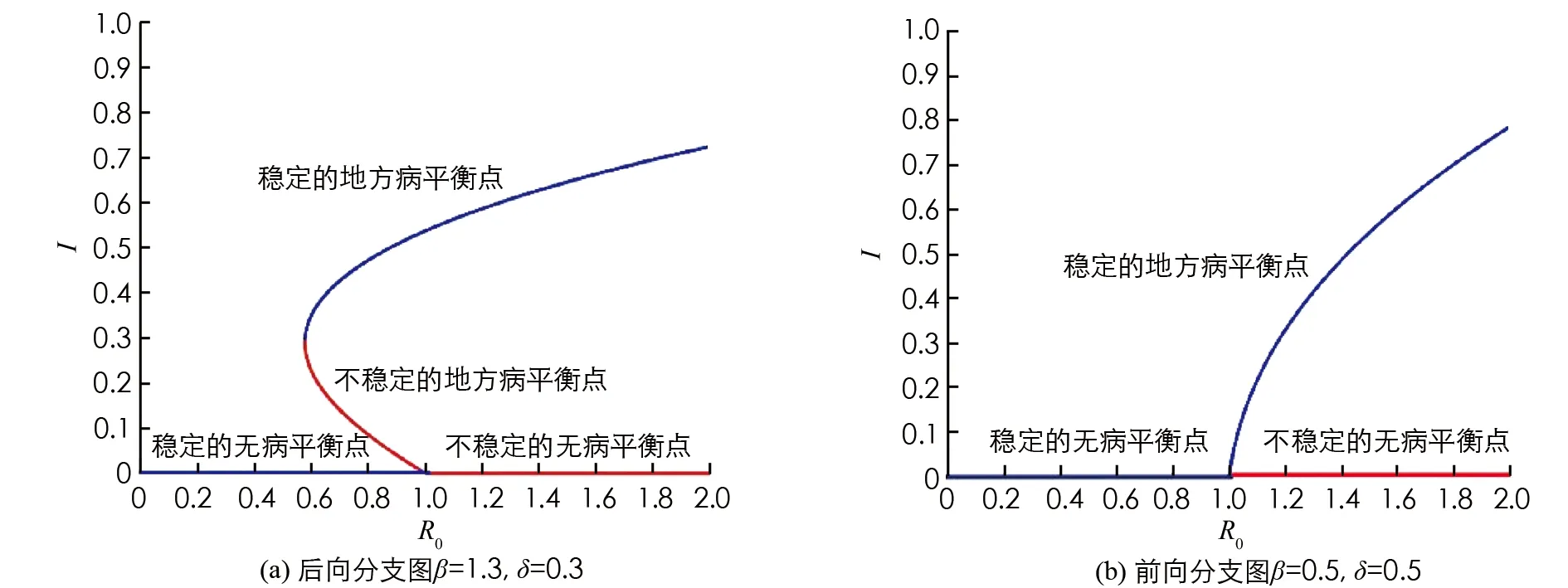
2) 當R0=1時, 若V′1(0) 3) 當R0<1時, 若V′1(0) 證令模型(2)的右端函數為0, 則有 V1(I)=V2(I) 其中 下面利用V1(I)和V2(I)的增減性及凹凸性進行分析. 由上述判斷可知,V1(I)是在[0, 1]上單調遞減的凹函數,V2(I)是[0, 1]上的凸函數. 又由于 則V1(0)>V2(0)等價于R0<1;V1(0)=V2(0)等價于R0=1;V1(0) 下面針對R0的3種情形(圖2)分別進行討論: 情形1 若R0>1, 有V1(0) 圖2 V1(I)和V2(I)的函數關系圖 情形2 若R0=1, 有V1(0)=V2(0)且V1(1)=0,V2(1)<0成立, 則當V′1(0) 成立時,V1(I)與V2(I)在[0, 1]內有且僅有一個交點, 否則將無交點(如圖2b). 情形3 若R0<1, 有V1(0)>V2(0)且V1(1)=0,V2(1)<0成立: 1) 當V′1(0) 2) 當存在一點I*使得V1(I*)=V2(I*)且V′1(I*)=V′2(I*)時, 兩交點重合為一個交點(如圖2d). 定理2(無病平衡點局部穩定性) 當R0<1時, 模型(2)的無病平衡點E0在D內局部漸近穩定; 當R0>1時,E0不穩定; 當R0=1時,E0為鞍結點, 其中當C>0時,E0為右鞍左結點; 當C<0時,E0為左鞍右結點. 證模型(2)的Jacobi矩陣為: 若R0-1<0, 即R0<1時,J(E0)有兩個負特征根, 此時模型(2)在E0處局部漸近穩定; 若R0-1>0, 即R0>1時,J(E0)的兩個特征根為異號實根, 此時E0為鞍點, 不穩定. 若R0-1=0,J(E0)具有一個零實部和一個負實部特征根, 屬于臨界情形下的奇點分析. 下面利用Liapunov-Schmidt更替法進行討論. 則將模型化為 (5) 2) 利用二元函數麥克勞林展式將右端函數展開, 得到如下系統: (6) 其中: ψ(I′,V′)=-βσI′V′ 3) 判斷臨界情形下的奇點穩定性. 令系統(6)的第二式右端函數為0. 當|x|?1時, 可利用待定系數法求解得到V′關于I′的函數. 令V′(I′)=a1I′+a2I′2+O(I′3), 則 可得 則V′關于I′的函數關系為: 將V′(I′)代入系統(6)第一式中, 得到降維后的系統: 其分支余維為1, 它的一個普適開折拓撲等價于: 通過分析其軌線拓撲分類, 可得在R0=1時, 無病平衡點E0為鞍結點. 現可分析得到以下結論, 令 則當C>0時,E0為右鞍左結點; 當C<0時,E0為左鞍右結點. 2) 若R0<1, 當滿足定理2條件3時模型中存在兩個地方病平衡點, 其中平衡點E1=(I1,V1)為鞍點始終不穩定, 平衡點E2=(I2,V2)是非鞍點. 對于所有非鞍點, 在條件D>0成立時均是局部漸近穩定的. 其對應的特征方程為: 其中 同時, 令D=δ[βδ(σ+1)+μ0-μ1+2(m′+θ+b)]. 定理4在R0=1時, 當條件β>βc成立, 或β<βc且δ<δc成立時, 模型(2)將會產生后向分支. 設系統(6)線性部分構成的矩陣Y在零特征根處所具有的非負左、 右特征向量分別為υ,ω. 其中 求得左右特征向量分別為: 其余分量二階導結果均為0. 則 在R0=1時, 若A>0,B>0, 系統會產生后向分支. 由于此時B>0成立, 只需 則有 β(1-σ)(mb+m′)δ(m′+θ+b)+β2σ(1-σ)δ(mb+m′)- βδ(m′+θ+b)2>(μ0-μ1)(m′+θ+b)2 (7) 從式(7)可以看出, 若滿足條件: (1-σ)δ(m′+θ+b)+βσ(1-σ)δ(mb+m′)>δ(m′+θ+b)2 即令 則當條件β>βc時, 系統可以產生后向分支. 而當β<βc時, 則只需滿足條件: 即當滿足條件 綜上所述, 當β>βc或β<βc時, 令δ<δc時, 模型(2)會產生后向分支. 值得注意的是, 定理2中的C>0等價于: 則在R0=1, 即無病平衡點為右鞍左結點時, 系統(2)會產生后向分支. 1) 固定參數μ0=0.08,μ1=0.8,δ=0.1分析了飽和治療函數的圖像(圖3). 圖3表明, 對于任意的δ>0, 飽和治療函數總介于μ0與μ1之間, 并且當I=δ時治療率達到中等水平, 說明包含醫院人均病床數在內的醫療資源數量與治療效果密切相關, 與此同時, 治療函數μ隨染病者密度I的增大而呈減小的趨勢并最終趨于最小恢復率, 從另一層面也表明了有限的醫療資源會限制疾病的治療. 圖3 飽和治療函數μ(δ, I)圖像 2) 固定參數μ0=0.1,μ1=0.6,θ=0.1,m′=0.4,m=0.6,σ=0.2,b=0.06,q=0.06, 且令人均病床數δ=0.1不變, 繪制出在β取不同值時系統(2)在相平面(V,I)內的軌跡圖(圖4). 圖4表明平衡點的個數及類型會隨β發生變化. 圖4(a)取參數β=0.7, 系統存在唯一的無病平衡點E0且穩定; 圖4(b)取參數β=1, 系統存在兩個正平衡點以及一個穩定的無病平衡點, 其中E1為鞍點,E2為穩定的結點; 圖4(c)取參數β=2.3, 系統存在一個不穩定的無病平衡點和一個穩定的結點. 圖4 模型在相平面(V, I)內軌跡圖(固定δ=0.1不變) 固定參數μ0=0.1,μ1=0.6,θ=0.1,m′=0.4,m=0.6,σ=0.2,b=0.06,q=0.06, 令有效接觸率β=0.5不變, 繪制出在δ取不同值時系統(2)在相平面(V,I)內的軌跡圖(圖5). 圖5表明平衡點的個數及類型會隨δ發生變化. 圖5(a)取參數δ=0.1, 系統存在唯一的無病平衡點E0且穩定; 圖5(b)取參數δ=0.001, 系統存在兩個正平衡點以及一個穩定的無病平衡點, 其中E1為鞍點,E2為穩定的結點. 圖5 模型在相平面(V, I)內軌跡圖(固定β=0.5不變) 3) 固定參數σ=0.6,m′=0.4,θ=0.7,m=0.6,b=0.2,q=0.2,μ0=0.1,μ1=0.6. 圖6(a)中假設β=1.3,δ=0.3, 此時模型產生后向分支, 在R0<1時既存在局部穩定的無病平衡點, 還存在兩個地方病平衡點, 其中不穩定的鞍點會隨R0的增加最終消失, 穩定的平衡點會逐漸趨于一個穩定水平. 圖6(b)中假設β=0.5,δ=0.5, 此時模型發生前向分支, 即R0<1時只存在一個穩定的無病平衡點, 而R0>1時模型存在唯一一個穩定的地方病平衡點. 研究后向分支的目的就是為避免選取使模型產生后向分支的參數, 以使疾病可以在R0<1時走向消亡. 圖6 模型后向分支和前向分支圖 根據本文得到的基本再生數式(3), 相較于文獻[14]得到的基本再生數: (8) 對于基本再生數式(3): 1) 當q=0時, 基本再生數(3)式轉化為 當m=0時, 基本再生數式(3)轉化為: 平衡點的相關結論與文獻[14]所得到的結果基本一致, 均得到了當基本再生數大于1時系統存在一個穩定的地方病平衡點和一個不穩定的無病平衡點; 當基本再生數小于1時, 除穩定的無病平衡點外系統還存在一個或兩個地方病平衡點, 其穩定條件類似. 相較于文獻[14]所得到的后向分支產生條件: (9) 依據本章得到的發生后向分支的條件: 可以看出, 在加入對易感者和接種者新生兒的預防接種因素后, 產生后向分支的參數δ范圍相對擴大, 這對于控制疾病而言, 參數δ在發生后向分支的范圍之外選取才有顯著作用. 本文基于乙型肝炎等傳染病, 考慮疫苗接種存在暫時性免疫且有一定接種效率的實際情況, 同時考慮到乙肝病毒可以垂直傳染, 建立了具有暫時性免疫倉室的一類考慮垂直傳染、 接種及醫院病床數的SIVS傳染病模型, 通過理論證明和定量模擬, 進一步完善具有暫時性免疫的傳染病研究, 并得到相關結論: 1) 當疾病的基本再生數大于1時, 隨時間推移疾病的染病者數量會逐漸趨于一個穩定水平; 當疾病的基本再生數小于1且人均醫院病床數大于一定值時, 隨時間推移疾病將逐漸消亡. 2) 當疾病接觸率β>βc或人均醫院病床數量δ<δc時, 疾病會發生后向分支, 此時無病平衡點在R0=1時為右鞍左結點. 這意味著在基本再生數小于1時, 既存在穩定的無病平衡點也存在穩定的地方病平衡點, 而控制疾病流行需要調節參數使其處于不發生后向分支的范圍. 3) 通過理論研究發現, 加入垂直傳染的傳播特點后, 基本再生數會相對增大并延長疾病走向消亡的時間; 而加入對易感者和接種者新生兒的預防接種措施后, 可以有效緩解基本再生數的增加, 控制疾病的流行, 同時發生后向分支的參數δ范圍也會擴大, 控制疾病時應使得接觸率和人均病床數處于不發生后向分支的范圍內. 4) 通過以上理論證明及數值模擬的結果, 可作如下解釋: 通過盡量減少易感者、 接種者與染病者的有效接觸, 極大的豐富包括人均病床數在內的醫療資源, 可以避免發生后向分支, 從而使疾病走向消無; 同時也可以通過增加對新生兒的預防接種比例和接種效率控制疾病. 在實際生活中, 曾有報道乙肝患者的子代由于未接種乙肝疫苗導致多年后患病并死亡的實例, 所以還可考慮對未發生垂直傳播的染病者新生兒進行接種的實際情形, 今后可根據這一特點繼續進行研究. 同時, 也可以考慮年齡結構、 心理效應及媒體報道等對此類疾病的影響.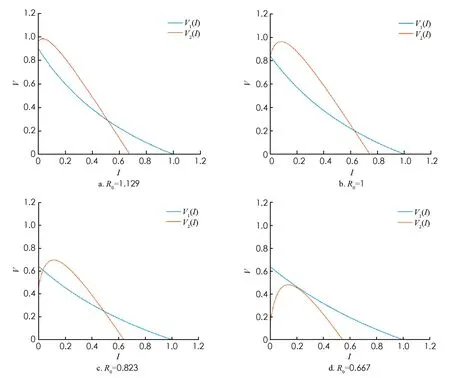
2.3 平衡點穩定性
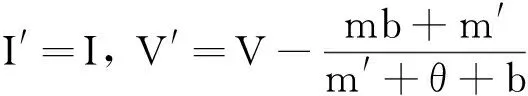
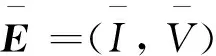
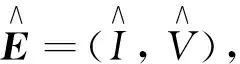
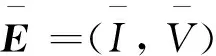
2.4 后向分支
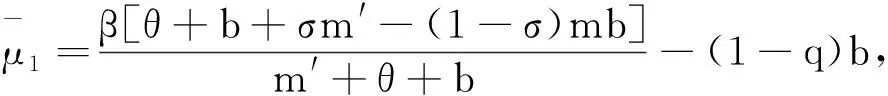
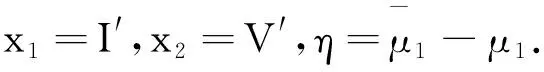
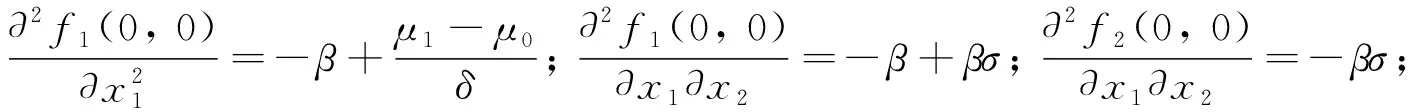
3 數值模擬
4 理論結果比較
4.1 基本再生數
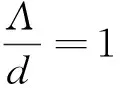
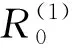
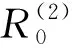
4.2 平衡點類型
4.3 后向分支條件
5 小結與展望

