基于Bi-LSTM 的航空發(fā)動機壽命預測

萬曉凡，徐澤宇，張營

（210037 江蘇省 南京市 南京林業(yè)大學）

0 引言

剩余使用壽命預測經過多年的發(fā)展，現主要以失效物理模型和數據驅動的方法[1]為主。盡管數據驅動法比較適合設備的剩余壽命預測，但是航空發(fā)動機衰退曲線的變化無明顯規(guī)律，所以結果不準確。失效物理模型就是通過采集設備的歷史衰退數據建立預測模型，但該方法對預測對象的假設條件較高且不適用于不相同線性的轉換。由此，依賴數據建模的相似性預測和機器學習預測更被研究者所接受[2-3]。張妍[4]等提出運用相似性進行剩余壽命預測適用于單退化量，但航空發(fā)動機運行環(huán)境多變且多傳感器，不能保證樣本后期相似程度變化小。

機器學習一般包括人工神經網絡（Artificial Neural Network，ANN）和支持向量機，若在兩者的基礎之上進行算法優(yōu)化則預測效果更佳。近年來，深度學習在機器學習領域一直是熱點，長短記憶神經網絡（Long Short-Term Memory，LSTM）、卷積神經網絡（Convolutional Neural Networks，CNN）和雙向長短時記憶神經網絡（Bi-directional Long-Short Term Memory，Bi-LSTM）在壽命預測領域發(fā)揮了重要作用。馬忠[5]等在CNN 的基礎上，使用不同的一維卷積核提取序列趨勢信息特征來更好地得到航空發(fā)動機工作過程中各個變量與剩余壽命之間的關系進行預測；曲星宇[6]等使用RNN-LSTM對故障進行診斷，優(yōu)化了網絡訓練的魯棒性和容錯性，但只憑借設備振動噪聲信號而對設備傳感器數據的忽略，其結果缺乏一定的嚴謹性；申彥斌[7]等提出一種基于Bi-LSTM 神經網絡用于軸承剩余使用壽命預測研究，該方法進一步提升了模型的預測準確率及泛化能力。

基于以上研究，本文提出在深度學習的基礎上，收集多個傳感器和飛行參數，訓練深度神經網絡，以根據時序數據或序列數據來預測數值。使用雙向長短期記憶 (Bi-directional Long Short-Term Memory，Bi-LSTM) 網絡，對網絡中的初始化函數和優(yōu)化器進行一定調整，旨在根據發(fā)動機中各種傳感器的時序數據來預測發(fā)動機的剩余使用壽命（預測性維護，以周期為單位度量）。最后，從NASA提供的航空發(fā)動機渦輪風扇發(fā)動機退化仿真數據集進行驗證，表明Bi-LSTM 預測效果較為理想。

1 Bi-LSTM 相關內容

1.1 Bi-LSTM 運行原理

循環(huán)神經網絡（Recurrent Neural Network，RNN）是深度學習算法之一，其輸入為一類序列（sequence）后，經過不斷迭代和神經節(jié)點間鏈式連接最后輸出。因為循環(huán)神經網絡自身具有記憶特性和共享參數等特點，利于參數挖掘和權重的合理分配，所以在非線性的序列學習上效果良好[8]。但RNN 并非完美無缺，若輸入過長，RNN 在不斷循環(huán)的過程中就會有梯度爆炸產生。總之，RNN 在信息輸入間距太遠情況下提取特征能力不盡如人意。長短記憶神經網絡（LSTM）是循環(huán)神經網絡（RNN）改進而來，其實LSTM 與RNN 相比增添了記憶功能，LSTM 多了輸入門、遺忘門和輸出門由此控制循環(huán)信息量。

無論是RNN 還是LSTM，都依靠前段時間的輸入經過訓練得出后段時間的輸出，但是輸出結果有時不僅僅由前段信息決定，還可能和未來息息相關[9]。要想前后時刻同時操作，需要兩相反方向的LSTM 疊加操作。Bi-LSTM 不僅克服了RNN 梯度爆炸問題，同時還擁有LSTM 推算優(yōu)點[8]。Bi-LSTM 原理如圖1 所示。

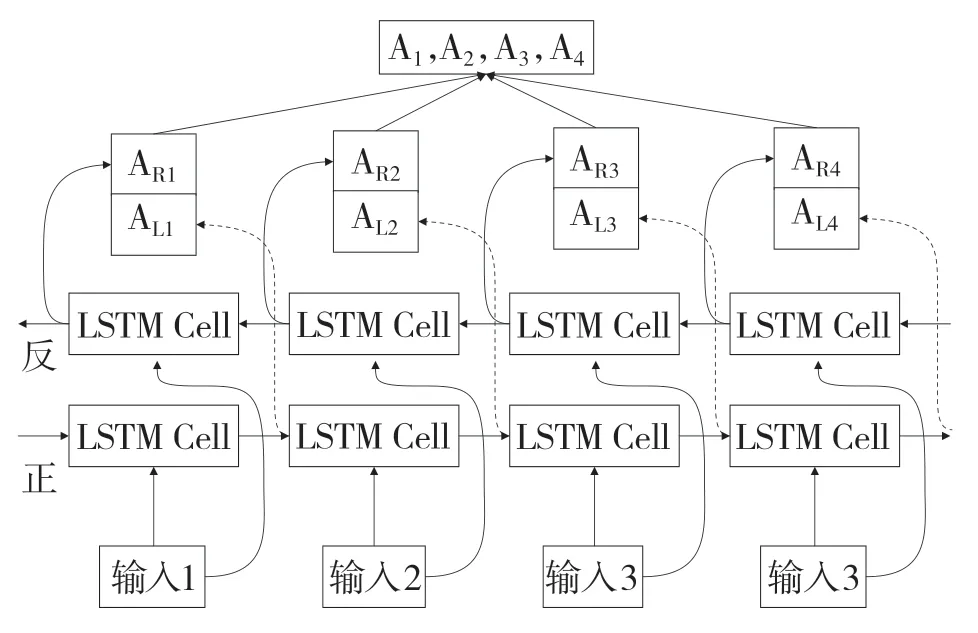
圖1 Bi-LSTM 工作原理Fig.1 Working principle of Bi-LSTM

如圖1 所示，把輸入分為4 部分進行編碼，前向傳播得到的組合為（AL1，AL2，AL3，AL4），反向傳播得到的組合是（AR1，AR2，AR3，AR4）。最后，將前后組合兩兩拼接得到4 個新組合（AL1，AR1）（AL2，AR2）（AL3，AR3）（AL4，AR4），即為（A1，A2，A3，A4）。

從圖1 中還可以看出，Bi-LSTM 相較于LSTM工作原理沒有什么較大的差異，和LSTM 一樣有輸入門、遺忘門和輸出門。

首先是遺忘門流程。輸入一串信息后，信息內容并非都是重要的，若能去除不重要的信息會有利于網絡訓練，這一步的操作就由遺忘門完成。ht-1為上一隱藏層狀態(tài)值，它和現輸入值xt一起進入隱藏層。激活函數sigmoid 為σ，它決定去留的信息。因為其值域為0 到1，當信息值趨于0 時丟棄，趨于1 時保留。遺忘門公式如式（1）：

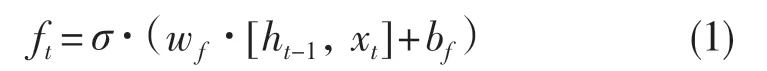
式中：w——權重；b——權重偏置。

其次為輸入門操作。負責保留信息的存放。得到候選值kt，然后通過遺忘門和輸入門舍去信息得到當前信息ct，具體操作如式（2）—式（3）：

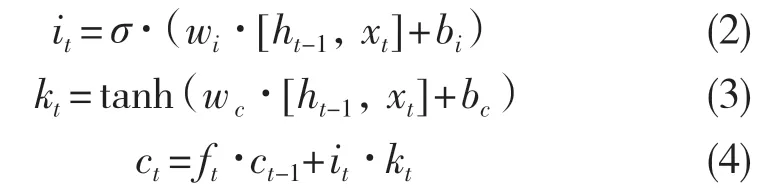
式中：it——輸入門。

最后為輸出操作。通過sigmoid 確定信息要輸出的內容，再將輸出信息同tanh 相乘確定要輸出的部分，具體操作如下：

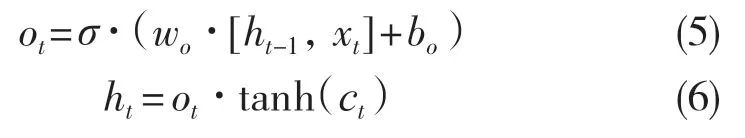
1.2 Bi-LSTM 過擬合優(yōu)化

在神經網絡訓練過程中會產生訓練誤差及測試誤差，若兩者在訓練整個過程中誤差相差不大且兩者誤差值都很小，說明預測模型構建良好；若兩者相差過大，也就是俗稱的過擬合[10-11]，這表示模型構建效果不佳，意思就是模型極度依賴現有的數據建模，一旦出現全新的數據將會影響預測的效果。

出現過擬合問題有2 種解決方法：一是數據量過少需增加訓練集，但是該方法成本較高；二是通過Dropout 層進行優(yōu)化。

Dropout 能改善過擬合問題的原理就是一定幾率的、隨機和暫時地停止部分神經元的訓練（如圖2 所示），也就是斷開神經元的連接，該方法在文獻[12]中提出。

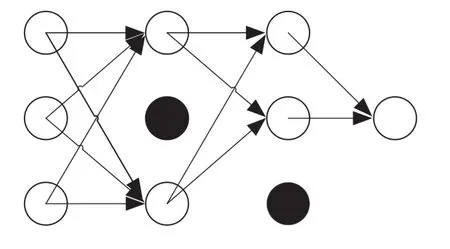
圖2 Dropout 工作原理Fig.2 Working principle of Dropout

在網絡模型訓練的過程中，不一定要全部的神經元都參與工作，可以讓部分神經元不參與訓練過程，在每次訓練時隨機斷開部分神經元的連接，這樣可以提高網絡的泛化能力。正常情況下在Dropout 層（丟棄率）設置為0.5 上下。

1.3 RMSprop 優(yōu)化器

深度學習中會引入損失函數（Loss Function），損失函數越小表示訓練結果越好，最小化（或最大化）任何數學表達式的過程稱為優(yōu)化。目前，使用較廣泛的優(yōu)化算法是梯度下降（Gradient Descent，SGD）。RMSprop 優(yōu)化算法是在SGD 基礎上演變而來，是自適應學習的一種。將其與Momentum 優(yōu)化算法對比發(fā)現，RMSprop 能更好地調整損失函數更新擺動幅度過大問題，同時收斂速度也有加快[13]。圖3 所示為二者優(yōu)化路線對比（左側虛線為Momentum，右側實線為RMSprop）。可看出RMSprop 幅度更小，因為它將微分平方加權平均數使用在權重和偏置的梯度上。

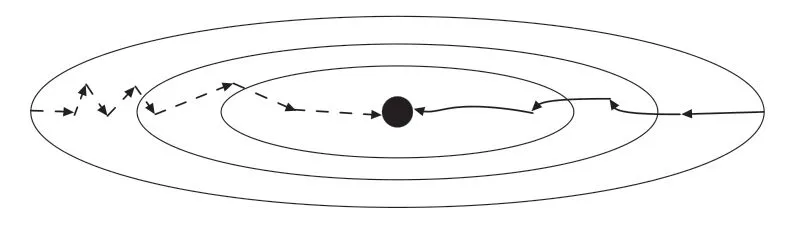
圖3 Momentum 與RMSprop 優(yōu)化路線對比Fig.3 Comparison of optimized routes between Momentum and RMSprop

2 案例證明

2.1 Bi-LSTM 預測模型

基于Bi-LSTM搭建預測流程框架，如圖4所示，訓練集預處理后由輸入層輸入，經過隱藏層和輸出層輸出結果。

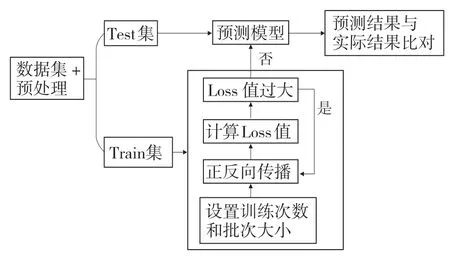
圖4 基于Bi-LSTM 搭建的預測流程圖Fig.4 Forecast flow chart based on Bi-LSTM

將數據分為若干部分，一部分組成訓練集（Train），剩下組成測試集（Test），如圖5 所示。其中訓練集在神經網絡的運作下進行數據建模并分出一部分進行效果檢測和參數調整。建模完成后，將測試集輸入模型得出結果。

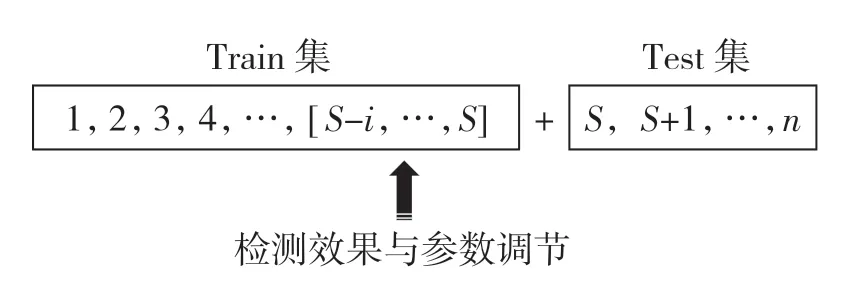
圖5 訓練集與測試集Fig.5 Training set and test set

2.2 案例數據來源

本文實驗數據來自NASA 的渦扇發(fā)動機退化模擬數據集（C-MAPSS）中的FD001，該數據包含100 個不完整序列，每個序列的末尾為相應的剩余使用壽命值，數據集為26 位數據，其中6～26 為傳感器，其他為飛行高度和循環(huán)次數。文獻[2]對21 個傳感器數據有詳細介紹。將數據集劃分成訓練集（Train）和測試集（Test），其中訓練集表示發(fā)動機從工作到失效整個過程數據，測試集為壽命結束前過程的整個數據，前者通過訓練找尋規(guī)律，后者進行測試驗證。

2.3 數據處理

數據歸一化（標準化）是對數據進行挖掘，因為評價指標不同，量綱也不同，由此會對分析造成一定影響，歸一化后的數據，各項指標數量級相同，可進行綜合對比。

本文數據集數據多，所以采取是z-score 標準化，這種方法給予原始數據的均值（mean）和標準差（standard deviation）進行數據的標準化[14-15]。經過處理的數據符合標準正態(tài)分布，即均值為0，標準差為1。轉換函數公式為：

式中：u——樣本均值；σ——樣本的標準差。

2.4 性能評價標準

為了測評模型訓練效果，本文會采用均方根誤差（root mean squared error,RMSE）作為評價指標，其能夠良好反應目標值與預測值存在多少誤差[16]，計算公式為：

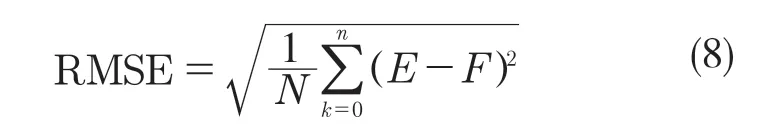
2.5 預測結果分析及對比

本模型實驗在Corei5-10300H，8-GB RAM，NVIDIA GTX 1650 GPU 環(huán)境下進行，操作系統為Windows 10，仿真軟件為MATLAB 2019a。設置丟棄率為0.5，否則會出現過擬合。優(yōu)化器為RMSprop，激活函數為Sigmoid，權重初始函數為Glorot，每批大小為20，最大迭代次數為300 次。

預測結果的RMSE 如圖6 所示。誤差（Error）為預測值減去真實值得到。由圖6 可見，RMSE 為17.943 3，除了極少誤差值落在兩側，部分誤差集于(-10，0]且分布緊湊，結果比較理想。

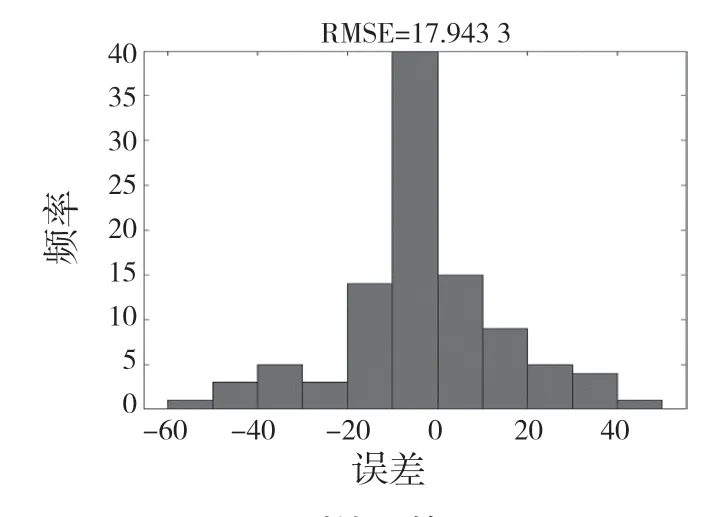
圖6 預測結果的RMSEFig.6 RMSE of predicted result

為證明使用RMSprop 算法的Bi-LSTM 預測在隨機情況下的誤差表現，在同樣的條件下進行5 次訓練得到RMSE，并且LSTM 網絡進行對比，結果如圖7 所示。圖7 中，上者為LSTM，下者為Bi-LSTM，可以看出下者比上者平均低約2.5%。

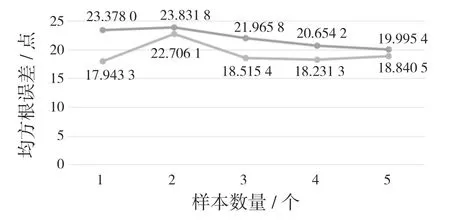
圖7 Bi-LSTM 和LSTM 隨機RMSE 對比Fig.7 Bi-LSTM and LSTM random RMSE comparison

還可通過抽取樣本在神經網絡中的預測結果圖，如圖8 所示為隨機樣本抽查效果圖，可以看出，Bi-LSTM 樣本預測剩余使用壽命（Remaining Useful Life，RUL）與真實RUL 線大致貼合。

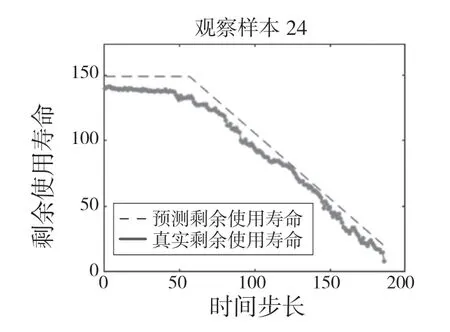
圖8 Bi-LSTM 樣本預測圖Fig.8 Sample prediction graph of Bi-LSTM

綜合以上對比結果可以看出，RMSprop 優(yōu)化算法的Bi-LSTM 整體預測效果要優(yōu)于LSTM。但有時會出現較大波動，因為航空發(fā)動機在多種故障下的規(guī)律難以捉摸，故在單工況下對其預測較為準確。

3 結語

本文總結了Bi-LSTM以及一些參數的特點后，提出基于該網絡的預測模型。通過航空發(fā)動機數據進行驗證，結果表明，單工況下基于RMSprop 優(yōu)化算法的Bi-LSTM 預測模型對航空發(fā)動機的剩余壽命預測相對于LSTM 預測模型要更加準確。