單相并網光伏系統的混合控制策略

張 爽，張 迪，薛 飛，徐恒山

（1.國網寧夏電力有限公司電力科學研究院，銀川 750001；2.三峽大學電氣與新能源學院，宜昌 443002）

化石能源的危機使光伏PV（photovoltaic）、風電等新能源得到了快速發展[1]。并網逆變器是將PV陣列發出的電能連接到公用電網的關鍵設備[2]。單級PV系統結構簡單[3]，變換效率較高[4]，但在功率波動時，難以同時獲得良好的并網特性和最大功率跟蹤MPPT（maximum power point tracking）特性[5]；兩級PV 系統可有效均衡并網特性和最大功率跟蹤特性[6]，其前級直流變換電路實現對PV陣列的功率跟蹤[7]，并將PV陣列的電壓通過直流變換器升高成為接近交流電網峰值電壓的直流母線電壓[8]，后級逆變電路將直流母線電壓變換為交流電壓且通過濾波后與電網連接[9]。

國內外學者對兩級并網PV系統的母線電壓穩定控制進行了大量研究[10-15]。文獻[10-13]采用傳統控制策略，在后級逆變器中引入對直流母線電壓的控制，通過控制逆變器的并網功率實現對直流母線電壓的調節，但當電網電壓發生波動時，會將交流側的波動傳遞到直流母線。文獻[14]提出基于PV板輸出能量、直流母線電容存儲能量和逆變器并網能量守恒控制的直流母線電壓調控策略，可提高逆變器對直流母線電壓的調控能力，但需要通過復雜的運算對3個環節的能量進行計算，加大了控制成本。文獻[15]將附加功率環引入到傳統控制策略中，可提高逆變器輸出電流對前級功率的跟蹤能力，在一定程度上，提高了直流母線電壓的穩定性，但依然不能解決電網電壓發生較大波動時，直流母線電壓會隨之波動的問題。目前，針對兩級并網PV 系統的電壓穩定性，幾乎所有研究均是從逆變側入手，通過優化并網逆變器的控制策略，提高逆變器對輸出功率或輸出電流的控制能力，實現對直流母線電壓的穩定控制，但忽視了直流變流器對直流母線電壓的潛在控制能力。

基于上述分析和研究背景，本文提出一種改進的混合控制策略，針對基于交錯Boost 變流器的PV系統，利用兩只高頻開關器件具有控制自由度較大的優點，同時在前級直流變換電路和后級逆變電路中引入直流母線電壓控制，提高兩級并網光伏系統中直流母線電壓的穩定調控能力。

1 兩級PV 系統

圖1 給出了兩級PV 系統的結構，由圖1 可知，其主要由PV 陣列、前級DC/DC 電路和后級DC/AC構成。前級DC/DC電路將PV陣列的電壓變換為直流母線電壓，后級DC/AC電路將直流母線電壓變換為交流電壓并通過濾波后與電網連接；濾波器由濾波電容和濾波電感組成，Cb為直流母線電容，ub為直流母線電壓。

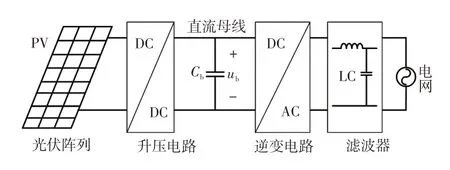
圖1 PV 并網系統的結構Fig.1 Structure of gird-connected PV system

交錯Boost 變流器可實現升壓和MPPT 的功能，H橋逆變器可實現PV并網功能。PV系統的電路如圖2所示。

圖2中，ipv、upv分別為PV陣列的電流和電壓；L1=L2=L為升壓電感；Q1～Q6為MOSFET 器件；s1～s6為Q1～Q6的控制信號；iQ1～iQ6為流過Q1～Q6的電流；iD1、iD2分別為流過二極管D1和D2的電流；idc為逆變器的輸入電流；Lac、Cac分別為交流側濾波電感和濾波電容；iac為并網電流；uac為電網電壓。

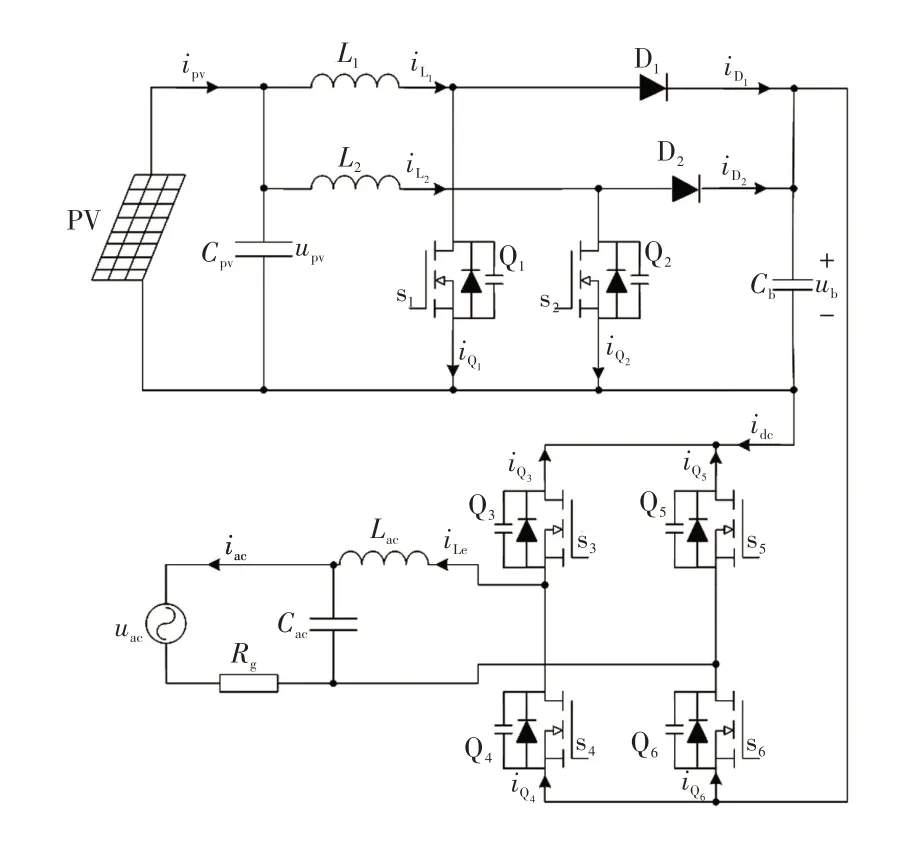
圖2 PV 并網系統的電路Fig.2 Circuit of gird-connected PV system

2 混合控制算法

2.1 PV 陣列模型

圖3 為PV 陣列的等效模型。其中，iph為光生電流；Dph為PN 結；Rsh、Rs分別為等效并聯電阻和串聯電阻；iD、ish分別為流過Dph和Rsh的電流。

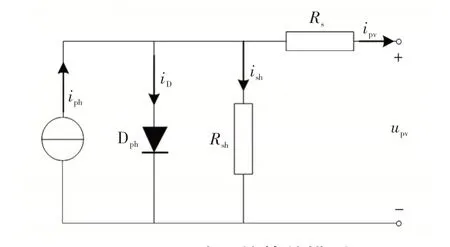
圖3 PV 陣列的等效模型Fig.3 Equivalent model of PV array

PV陣列輸出電流ipv可表示為

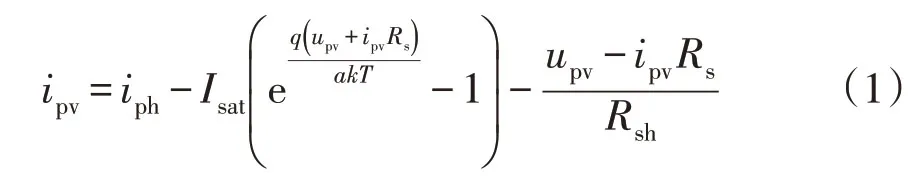
式中：Isat為反向飽和電流；k為波茲曼常數；q為電荷量；T表示溫度；a為二極管的品質系數。反向飽和電流Isat可表示為

式中：Uo,pv為PV 的開路電壓；UT,pv為溫度T時PV的電壓。

由式（1）可得upv和ipv的關系為

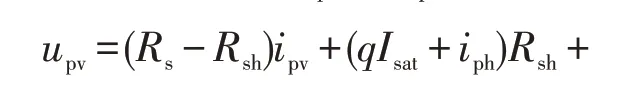
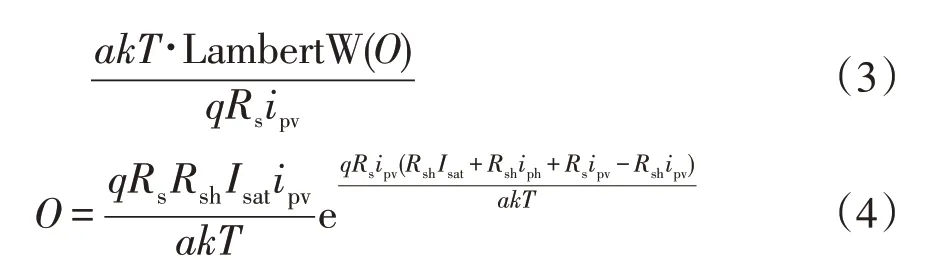
式中，LambertW()為朗伯W函數。

PV陣列的輸出功率ppv可表示為

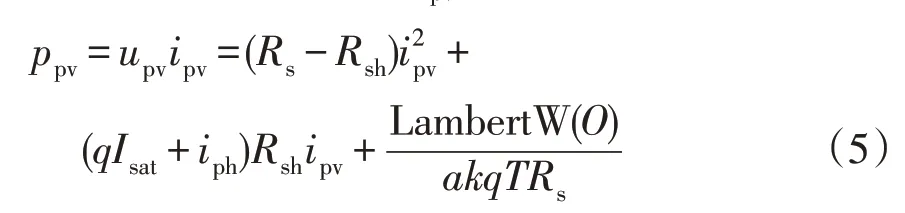
PV 板采用2 塊型號為APM36P30W82x36 的多晶硅串聯構成，其短路電流Isc=1.94 A，開路電壓Uo,pv=43 V，品質系數a=1.3，串聯電阻Rs=0.2 Ω，并聯電阻Rsh=415 Ω。PV板的ppv與upv的關系曲線如圖4所示。

由圖4 可以看出，PV 陣列的輸出功率ppv隨其電壓upv發生變化，當輸出電壓upv=Um時，PV板的輸出功率達到最大值ppv,max。為了提高PV 功率的利用率，需要通過一定的控制策略使PV 陣列在穩態時工作在最大功率點(Um,ppv,max)，它的本質做法是控制DC/DC 電路，使其輸入阻抗等于PV 陣列的內阻抗，從而保證PV陣列工作在最大功率點。

圖4 ppv 與upv 的關系曲線Fig.4 Curve of relationship between ppv and upv

2.2 MPPT 算法

國內外學者對MPPT 算法的研究較多，常用的MPPT 算法是增量法，采用增量法實現PV 系統MPPT 的典型流程如圖5 所示。該流程主要步驟如下：

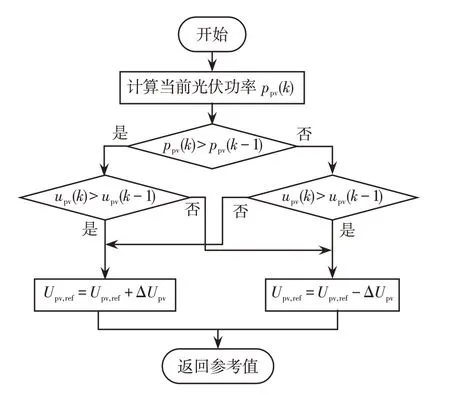
圖5 增量電壓法實現MPPT 的流程Fig.5 Flow chart of realizing MPPT based on incremental voltage method

步驟1根據PV 陣列當前開關周期的輸出電壓upv(k)和電流ipv(k)，計算當前開關周期PV 陣列的輸出功率ppv(k)；

步驟2將當前開關周期PV陣列輸出功率ppv(k)與上一開關周期PV陣列輸出功率ppv(k-1)相比較，為PV陣列參考電壓Upv,ref的整定提供判斷依據；

步驟3比較當前開關周期PV 陣列輸出電壓upv(k) 與上一開關周期PV 陣列的輸出電壓upv(k-1)，為PV 陣列參考電壓Upv,ref的整定提供判斷依據；

步驟4結合PV 陣列輸出電壓和輸出功率的比較結果，對PV陣列輸出電壓的參考值進行整定。

采用電壓外環-電流內環的雙環控制，通過MPPT 算法得到PV 陣列輸出電壓的參考值Upv,ref后，將Upv,ref與其實時電壓upv相比較，并通過電壓環控制器的調節即可得到PV 陣列電流ipv的參考值Ipv,ref；Ipv,ref與實時電流ipv相比較，并經過電流內環的調節，得到調制信號v1；v1通過脈沖寬度調制PWM（pulse width modulation）發生器的計算可得到MOSFET器件的控制信號，進而控制升壓電流實現MPPT功能，其完整的控制邏輯如圖6所示。

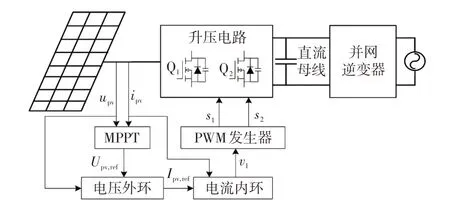
圖6 MPPT 算法的原理Fig.6 Schematic of MPPT algorithm

由圖6 可以看出，控制流程雖然可以實現MPPT 功能，但其控制過程沒有對直流母線電壓的穩定性進行考慮，而直流母線電壓的穩定與否直接影響并網逆變器的穩定性。當PV陣列發生較大功率波動時，直流母線電壓也會隨之波動；當PV系統接入弱電網系統時，可能導致并網點電壓波動，進而對電網產生不良影響。此外，頻繁的功率波動引起直流母線電壓頻繁變化，在此過程中伴隨的過充電會對母線電容的壽命造成影響，甚至出現過壓擊穿危險。

為解決傳統MPPT算法在對直流母線電壓控制上的缺陷，針對交錯Boost 變流器作為升壓電路的PV 并網系統，提出一種兼顧直流母線電壓穩定性的混合控制策略。

2.3 直流母線電壓的穩定控制

圖7 為提出的混合控制策略框圖，其中，Δppv為PV陣列的功率增量，Δppv,ref為PV陣列功率增量的參考信號。與傳統MPPT 控制策略不同，該控制策略充分調動了交錯Boost 變流器的控制靈活性，當PV 功率波動較小，即Δppv＜Δppv,ref時，為了平衡交錯Boost 變流器中2 只MOSFET 器件的功率，使2只MOSFET器件都工作在MPPT模式下，s1和s2均可通過p1計算得到，由于PV功率波動較小，直流母線電壓的變化范圍也較小，此時不對直流母線電壓進行嚴格控制；當PV 功率發生劇烈波動，即Δppv≥Δppv,ref時，由于功率波動較大，如果不對直流母線電壓進行調控，可能導致直流母線電壓發生劇烈變化，此時，為了保持穩定的直流電壓，利用一只MOSFET 器件實現MPPT 功能，并使另一只MOSFET 工作在直流母線電壓外環，同時實現MPPT 和直流母線電壓穩定的功能。需要說明，當PV 功率處于劇烈變化時，即使采用傳統算法，也很難在極短時間內，通過調節變流器的工作狀態使PV 陣列工作在最大功率點。因此，本文提出的混合控制算法是在這個過程中對直流母線電壓進行穩定控制，既不損失最大功率點的追蹤能力，又能對功率波動時的電壓波動進行消除。

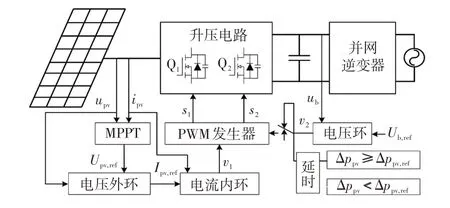
圖7 混合控制算法的框圖Fig.7 Block diagram of hybrid control algorithm

在采用上述混合控制策略時，Δppv,ref的取值會影響母線電壓的穩定性和PV 陣列的MPPT 能力。如果Δppv,ref取值較小，會出現母線電壓環過早介入的現象，導致變流器在純MPPT 模式與混合模式之間頻繁切換，造成MPPT 和母線電壓穩定二者之間的紊亂；如果Δppv,ref取值過大，會使母線電壓難以在功率波動時介入控制，削弱母線電壓的穩定性；在極端情況下，如果Δppv,ref取值很大，超過了功率波動邊界值，會導致并網變流器完全工作在純MPPT模式下，母線電壓環的功能完全被去除，不能在功率波動時對母線電壓進行穩定控制。

3 仿真驗證

為證實混合控制策略在母線電壓穩定控制和MPPT上的能力，在仿真軟件中搭建一組PV并網仿真模型，MOSFET的最大占空比為0.95，其他參數見表1。

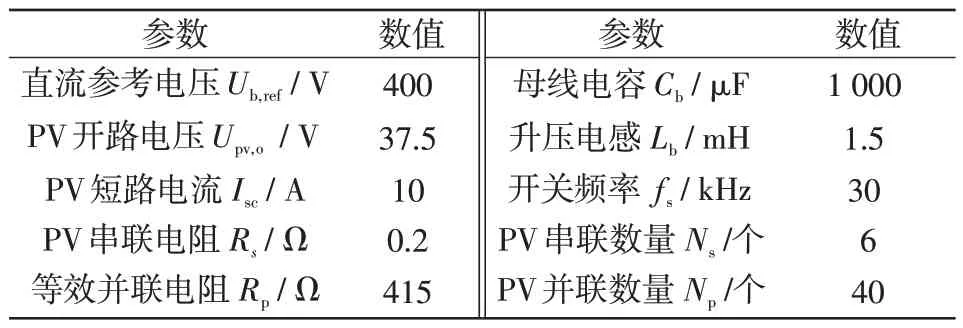
表1 PV 的電氣參數Tab.1 Electrical parameters of PV

3.1 階躍功率擾動仿真

圖8 為在采用傳統MPPT 控制策略下，當光照強度J從0 階躍上升到1 kW/m2的過程中，直流母線電壓ub的波動情況。由圖8可以看出，隨著J的增加，ub的波動范圍隨之增加，當t=1 s，J由0 kW/m2上升到0.25 kW/m2時，ub的波動范圍為395～404 V，波動量Δub=9 V；當t=2 s，J由0.25 kW/m2上升到0.50 kW/m2時，ub的波動范圍為389～409 V，波動量Δub=20 V；當t=3 s，J由0.50 kW/m2上升到0.75 kW/m2時，ub的波動范圍為380～413 V，波動量Δub=33 V ；當t=4 s，J由0.75 kW/m2上升到1.00 kW/m2時，ub的波動范圍為370～419 V，波動量Δub=49 V。

圖8 傳統MPPT 算法下階躍遞增光照強度時的母線電壓波形Fig.8 Waveform of bus voltage for traditional MPPT algorithm when irradiance increases in step way

圖9 為在階躍遞增光照強度下，采用傳統MPPT控制策略時，PV陣列功率ppv與電壓upv之間的仿真結果。由圖9 可以看出，傳統MPPT 控制策略可以保證PV變流器在恒定功率時工作在最大功率點。

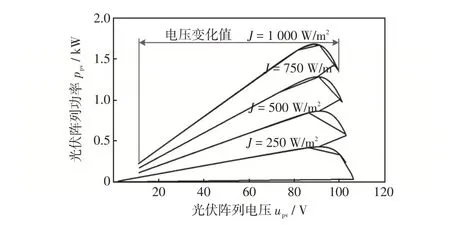
圖9 傳統MPPT 算法下階躍遞增光照強度時ppv 與upv的仿真結果Fig.9 Simulation result of relationship between ppv and upv for traditional MPPT algorithm when irradiance increases in step way

圖10 為在采用本文提出的混合控制策略下，當光照強度J由0 階躍上升到1 kW/m2的過程中，直流母線電壓ub的波動情況。由圖10 可以看出，隨著J的增加，ub的波動范圍隨之增加，但與圖8中的波動相比，在高功率狀態下，圖10中的波動量較小。當t=1 s 時，J由0 kW/m2上升到0.25 kW/m2時，ub的波動范圍為397～409 V，波動量Δub=12 V ；當t=2 s 時，J由0.25 kW/m2上升到0.50 kW/m2時，ub的波動范圍為395～409 V，波動量Δub=14 V ；當t=3 s 時，J由0.50 kW/m2上升到0.75 kW/m2時，ub的波動范圍為392～414 V，波動量Δub=22 V ；當t=4 s 時，J由0.75 kW/m2上升到1.00 kW/m2時，ub的波動范圍為389～416 V，波動量Δub=27 V。

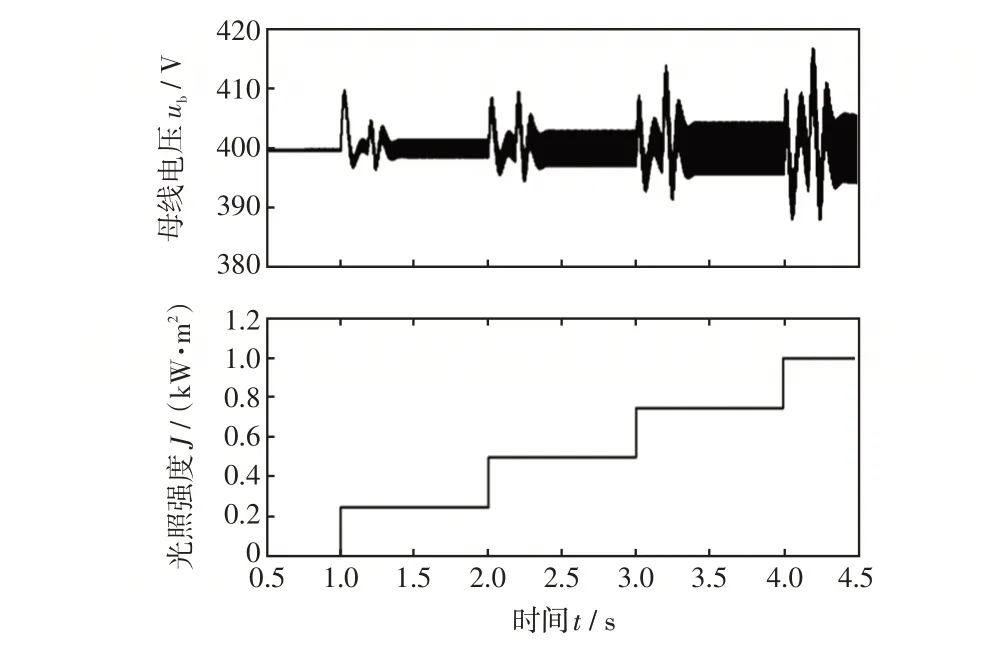
圖10 混合控制策略下階躍遞增光照強度時的母線電壓波形Fig.10 Waveform of bus voltage under hybrid control strategy when irradiance increases in step way

圖11 為階躍遞增光照強度下采用本文提出的混合控制策略時PV陣列功率ppv與電壓upv之間的仿真結果。由圖11可以看出，①相比于圖9中的仿真結果，當PV功率波動時，變流器能夠以更快的速度讓PV陣列實現MPPT，這是因為圖11中ppv從一個穩定的功率點跳變到另外一個穩定的功率點的過程中，在混合控制策略下PV 陣列的電壓變化值較小，而兩種控制策略采用相同的ΔUpv步長，因此從一個穩態到另外一個穩態的開關次數較少；②在混合控制策略下，變流器能夠快速地使PV 陣列實現最大發電功率，這是因為，提出的控制策略能夠有效減少變流器功率到達穩態過程的開關次數，讓PV陣列以更快的速度進入到最大功率點。

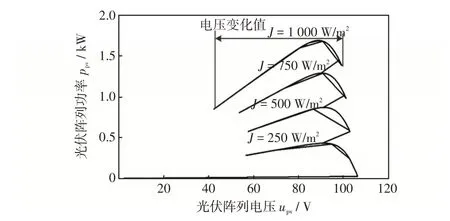
圖11 混合控制策略下階躍遞增光照強度時ppv 與upv 的仿真結果Fig.11 Simulation result of relationship between ppv and upv under hybrid control strategy when irradiance increases in step way

3.2 隨機光照強度仿真

圖12 給出了當Δppv,ref=100 W 時的仿真結果，為了與實際情況接近，光照強度的數值通過隨機函數得到。當光照強度如圖12 中發生隨機變化時，母線電壓ub的波動范圍為373～416 V，其波動量Δub=33 V。

圖13 為隨機光照強度下采用傳統MPPT 算法時PV 陣列輸出功率ppv與電壓upv之間的關系，且所采用的的隨機光照強度與圖12中的隨機光照強度一致。由圖13 可以看出，傳統MPPT 算法能使PV陣列大部分時間工作在最大功率點區域。由圖12～13的仿真結果可以得出，在隨機光照強度下，傳統MPPT 算法能使PV 陣列大部分時間工作在最大功率點區域內，但母線電壓會在隨機光照強度下發生較大波動。

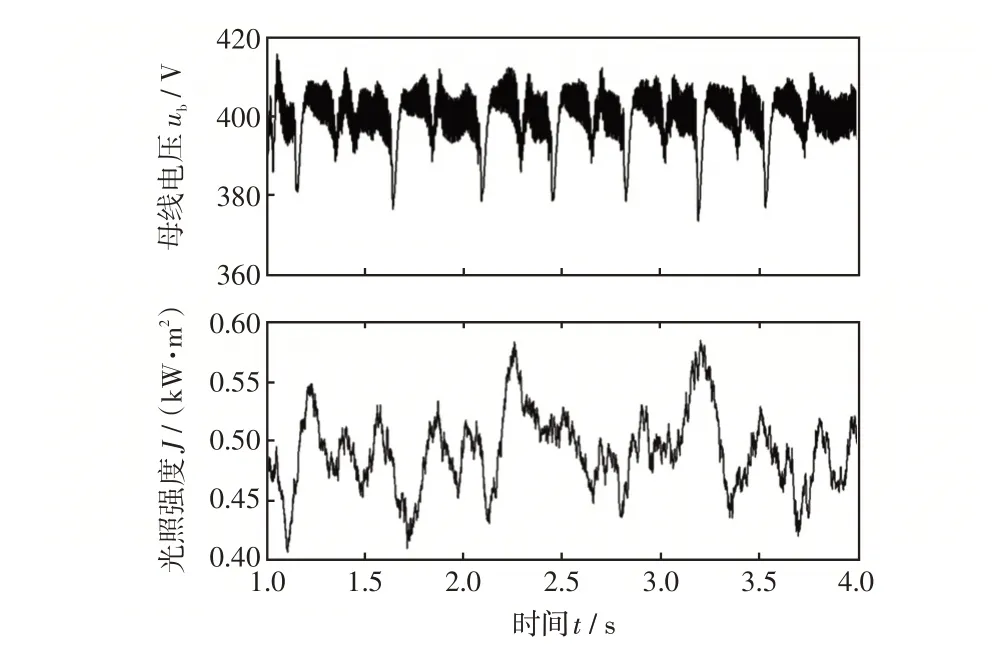
圖12 傳統MPPT 算法下隨機光照強度的母線電壓波形Fig.12 Bus voltage waveform for traditional MPPT algorithm with random irradiance

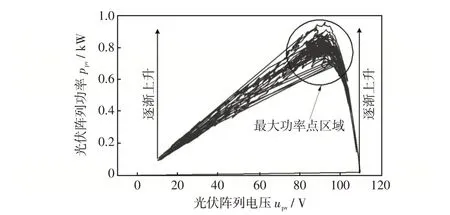
圖13 傳統MPPT 算法下隨機光照強度時ppv 與upv 的仿真結果Fig.13 Simulation result of relationship between ppv and upv for traditional MPPT algorithm with random irradiance

圖14 為采用本文提出的混合控制策略時直流母線電壓和光照強度的仿真結果，為了增加實驗的公平性，圖14 中的光照強度與圖12 中的光照強度變化趨勢一致。相比于圖12 中的仿真結果，圖14中直流母線電壓的波動量更小，波動范圍為390～408 V，這說明提出的混合控制策略能夠更好的對直流母線電壓進行控制，減小直流母線的電壓紋波。

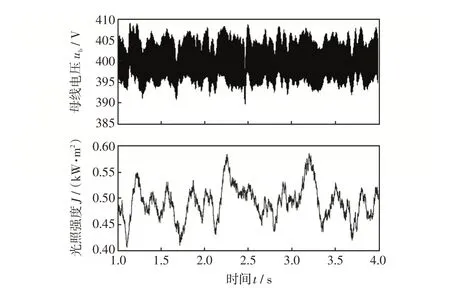
圖14 混合控制策略下隨機光照強度的母線電壓波形Fig.14 Bus voltage waveform under hybrid control strategy with random irradiance

圖15為采用提出的混合控制策略時PV系統的功率跟蹤結果。與圖13 中的功率跟蹤效果相比，圖15 中PV 系統以更大的概率停留在最大功率區域，說明混合控制算法的功率跟蹤效果良好。

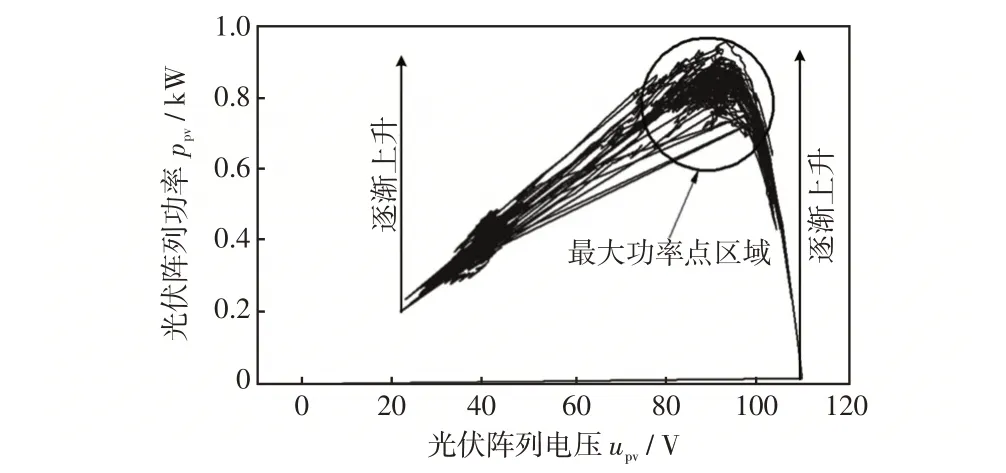
圖15 混合控制策略下隨機光照強度時ppv 與upv 的仿真結果Fig.15 Simulation result of relationship between ppv and upv under hybrid control strategy with random irradiance

由圖12～15 可以看出，本文提出的混合控制策略既保證了單相并網PV系統的MPPT能力，還能對PV系統的直流母線電壓進行穩定控制。相比于傳統的MPPT 控制策略，所提出的控制策略可有效的穩定直流母線電壓，減小直流母線電壓在擾動輸入工況下的波動，有利于降低直流母線電容的電壓應力、提高直流母線電容的使用壽命。

4 實時在環實驗驗證

為了進一步驗證控制策略的有效性，在Matlab/Simulink和RT-Lab軟件中搭建實時在環仿真模型，并在5600仿真機中進行實驗。圖16給出了實時在環仿真平臺，其中，錄波儀用于記錄實驗波形，上位機通過仿真器將Matlab/Simulink 中的控制程序下載到控制器中，控制器采用TI公司的數字控制芯片DSP（digital signal processor），DSP的型號為F28335；為了方便表示PV 功率ppv和光照強度J，在RT-Lab中將PV功率ppv和光照強度J轉換為電壓信號，電壓信號的10 V分別對應ppv和J的1 kW和1 kW/m2，錄波儀每豎格表示10 V電壓。

圖16 實時在環仿真平臺Fig.16 Real-time hardware-in-the-loop simulation platform

圖17～18分別為采用傳統MPPT控制策略和混合控制策略時得到的母線電壓ub、光照強度J和光伏功率ppv的實驗波形，ub的參考值為400 V。將圖17 和圖18 中的光照強度J采用相同的信號源，以增加對比實驗的公平性。為了方便分析直流母線電壓ub的波動量，在測量ub時，將其測量通道置于交流檔，對直流分量進行濾除。

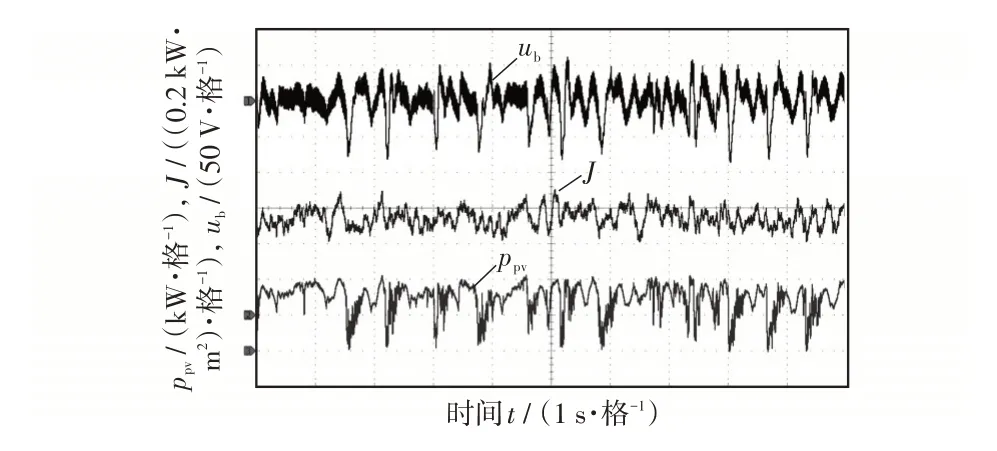
圖17 傳統MPPT 控制策略下的實時仿真波形Fig.17 Real-time simulation waveforms under traditional MPPT control strategy

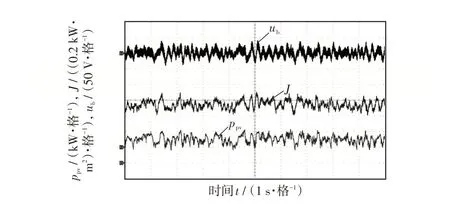
圖18 混合控制策略下的實時仿真波形Fig.18 Real-time simulation waveforms under hybrid control strategy

在圖17 中，ub交流分量的最大值和最小值分別為64 V 和-83 V，電壓的波動量約為147 V；ppv的最大值和最小值分別約為2.18 kW 和0 kW。在圖18中，ub交流分量的最大值和最小值分別為39 V和-40 V，電壓的波動量約為79 V；ppv的最大值和最小值分別約為2.18 kW 和0.8 kW。相比之下，在本文提出的混合控制策略下，直流母線電壓的波動量從147 V 減小到79 V，最低功率由0 kW 提升到0.8 kW，提高了PV系統的利用率。同時，從實驗結果還可看出，圖18 中的ppv與J的變化趨勢一致，而圖17 中的ppv卻對光照量J的跟蹤出現了一定誤差，說明混合控制策略能夠更好地對PV 陣列的最大功率進行跟蹤。

5 結語

針對單相并網PV 系統，提出一種混合控制策略。通過理論分析、仿真實驗和實時在環實驗驗證了本文提出的混合控制策略既能保證傳統算法的MPPT能力，又能實現對直流母線電壓的穩定控制，有利于減小直流母線電壓的波動，提升直流母線電容的使用壽命，提高單相并網PV 系統的穩定性和可靠性。