離心壓縮機蜂窩阻尼密封動力特性及轉子穩定性*
姚 潔 孟繼綱 胡 永 張忠偉
(沈陽鼓風機集團股份有限公司 遼寧沈陽 110869)
隨著現代離心壓縮機向高速化、大型化方向發展,機組在運轉過程中受到傳統迷宮密封氣流激振力的作用,面臨的轉子失穩而導致停機或碰磨事故的風險大大上升。1985年,蜂窩阻尼密封首次用于解決航天飛機高壓氧渦輪泵的流體激振問題[1],因其獨特的阻尼特性,可明顯提高旋轉機械轉子系統的穩定性,此后在透平機械中得到大量應用。ZEIDAN等[2]介紹了在背靠背和直通型2種離心壓縮機平衡盤密封處改造蜂窩密封,從而成功解決壓縮機失穩問題的案例。JAY和FRANCK[3]介紹了蜂窩密封成功應用于解決汽輪機次同步振動的案例。NORONHA等[4]介紹了蜂窩組合式密封應用于一臺高壓直通壓縮機中解決振動的問題。
蜂窩密封動特性的快速準確計算是保障轉子穩定性預測的關鍵基礎,目前蜂窩密封動力特性的研究方法主要包括數值方法和實驗方法。實驗方法[5-7]成本較高,耗時較長。數值方法中傳統的單控體[8]和雙控體模型[9-10]雖然計算效率高,但在結構和工況復雜情況下誤差較大[11],均不適合快速工程應用。隨著CFD技術發展,近年來國內外學者開始采用該方法研究密封動特性,并形成了一套比較成熟的理論和計算方法。國外學者MOORE[12]給出了偏心穩態計算模型,其計算方法簡便,但適用面窄;CHOCHUA和SOULAS[13]提出了基于動網格技術的單頻渦動模型,可計算單個渦動頻率下的動特性系數。國內學者李軍團隊[14-15]和孫丹團隊[16-17]研究了多頻橢圓渦動模型,通過少量計算可獲得多個頻率下的轉子動力特性系數,且計算精度高,對復雜結構和運行工況有良好的適應性。但關于蜂窩密封及轉子穩定性的研究較少。
本文作者從蜂窩密封動特性分析入手,采用CFD非定常動網格技術和多頻渦動求解模型,研究了蜂窩密封動特性系數,并與同條件下的迷宮密封進行對比,分析了蜂窩密封在實際壓縮機轉子上的穩定性效果。研究成果為蜂窩密封工程應用提供了依據。
1 密封動力特性理論求解模型
1.1 密封氣流力線性化模型
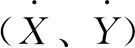
(1)
式中:K為直接剛度;k為交叉剛度;C為直接阻尼;c為交叉阻尼。
其中交叉剛度為轉子失穩力的主要來源,該值越大,轉子穩定性越差。
1.2 轉子多頻橢圓渦動模型
為求解8個動力特性系數,需要在轉子上施加2組渦動激勵,多頻橢圓渦動激勵方程[17]為
(2)
式中:Ωi為轉子渦動頻率;a、b為轉子渦動幅值;N為轉子渦動所包含的頻率數。
將式(2)進行快速傅里葉變換(FFT),可得頻域內氣流激振力與動力特性系數和小擾動量的關系式為
(3)
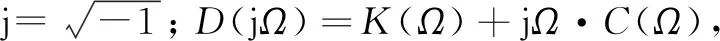
通過求解式(3)可得:
(4)
(5)
則蜂窩阻尼密封動力特性系數求解公式為
K(Ω)=Re(D(jΩ))
(6)
k(Ω)=Re(E(jΩ))
(7)
(8)
(9)
為了綜合反映蜂窩阻尼密封對轉子穩定性的影響,定義有效剛度和有效阻尼:
Keff=K+Ω·c
(10)
Ceff=C-k/Ω
(11)
2 密封動力特性數值求解
2.1 求解模型
圖1所示為蜂窩密封。文中研究的蜂窩密封結構如圖2所示,蜂窩芯格關鍵尺寸為對邊距B,蜂窩壁厚b,蜂窩孔深h。蜂窩密封的詳細結構參數見表1。

圖1 蜂窩密封
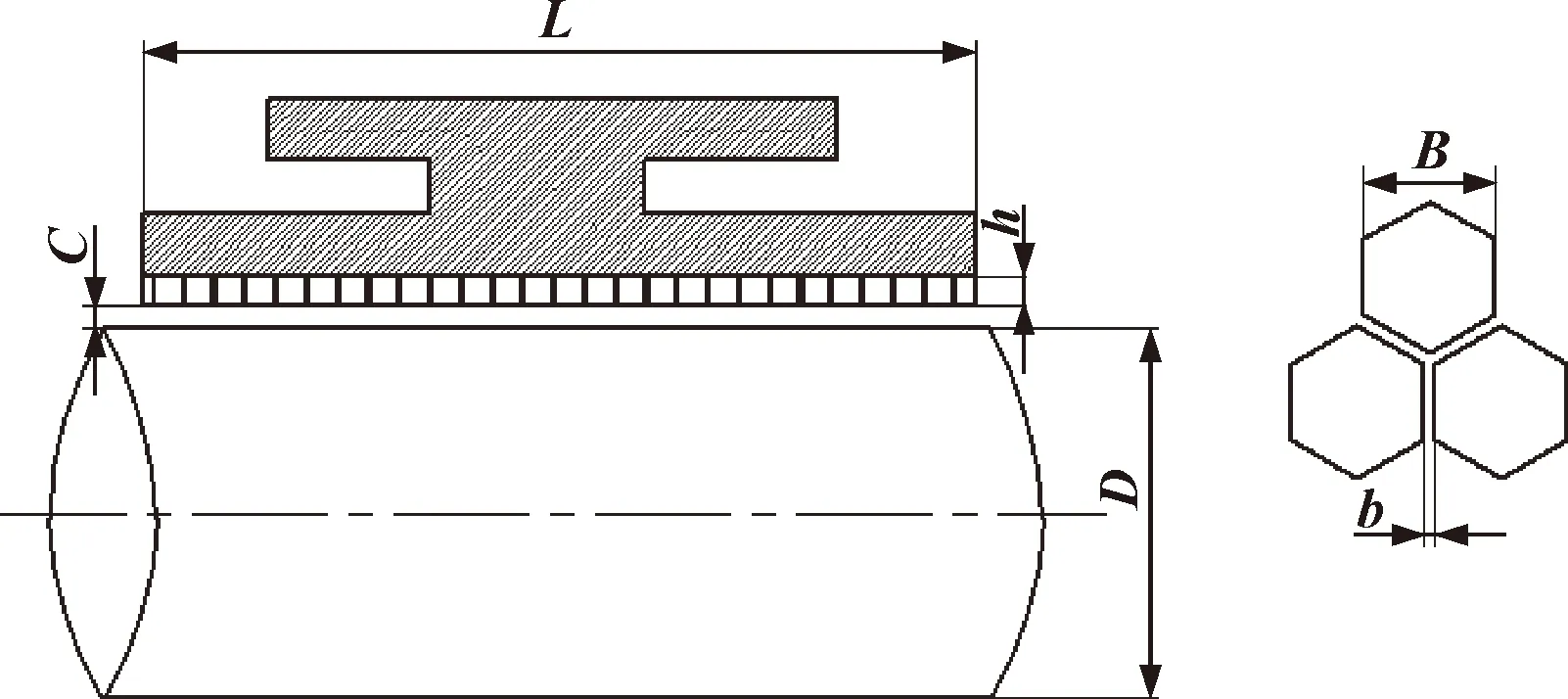
圖2 蜂窩密封結構示意
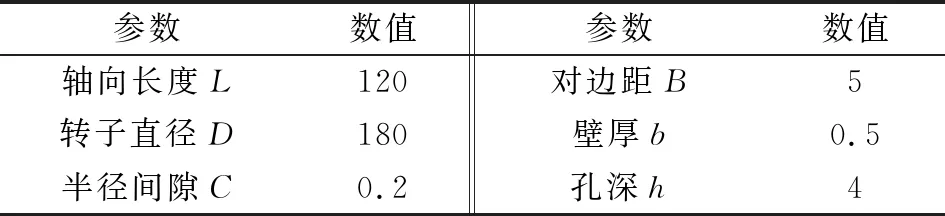
表1 蜂窩密封結構參數 單位:mm
2.2 網格劃分
考慮到蜂窩密封流場結構較復雜,將密封間隙和密封腔網格分別處理。密封間隙部分由于尺寸小,流動變化大,對其徑向網格進行加密處理,保障網格密度。整體網格為360°全三維結構化網格,經網格無關性驗證后,單元數量控制在300萬。圖3所示為蜂窩密封網格示意。
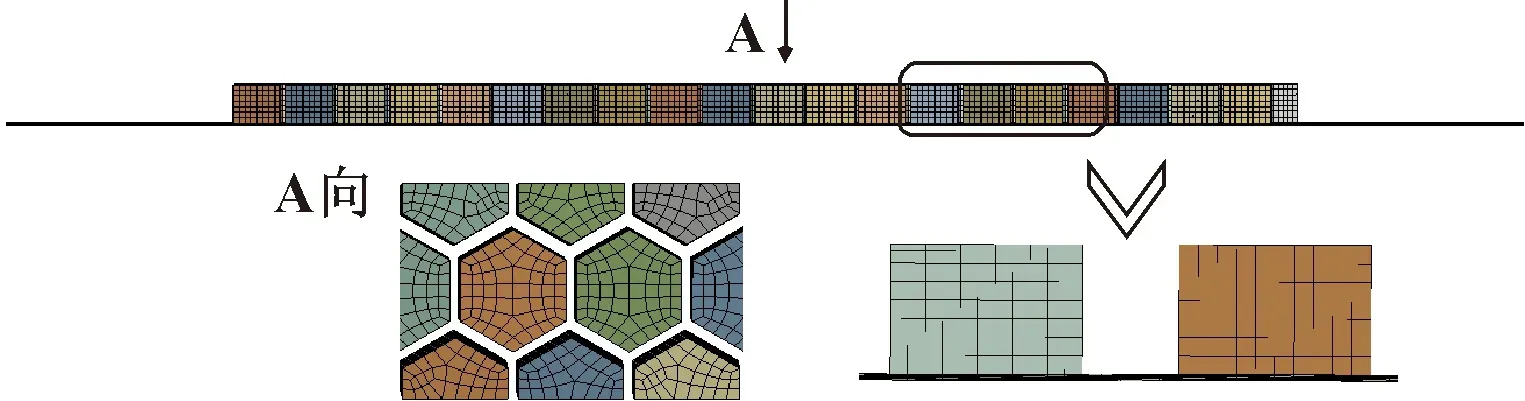
圖3 蜂窩密封網格示意
2.3 載荷和邊界條件
文中蜂窩密封計算域流體為理想空氣,進出口邊界為壓力邊界,轉子外表面為旋轉壁面,蜂窩腔室壁為靜子面,設為無滑移固體壁面。圖4所示為密封模型的邊界條件示意,表2給出了密封計算工況。
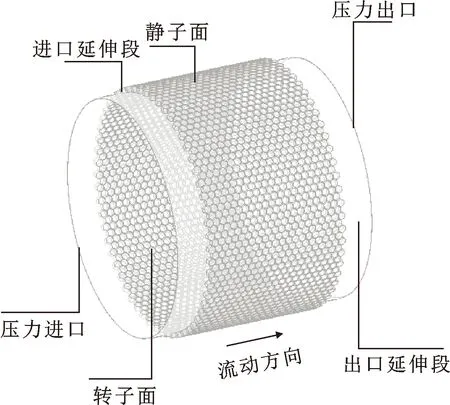
圖4 蜂窩密封計算模型

表2 密封運行工況
采用多頻渦動模型,選取基頻40 Hz,頻率個數N=7,求解渦動頻率f在40、80、120、160、200、240、280 Hz下的密封動特性系數。為使渦動滿足小位移渦動理論,文中將轉子渦動振幅取為a=0.01C,b=0.005C,C為密封半徑間隙。計算時間步長0.000 1 s。
3 計算結果及分析
3.1 渦動位移與氣流力分析
圖5和圖6分別給出了CFD計算得出的轉子面渦動位移(Y方向激勵)時域圖和經過快速傅里葉變換后得到的位移頻域圖。圖7和圖8分別給出了密封氣流力時域圖和經過快速傅里葉變換后的氣流力頻域圖(Y方向激勵)。
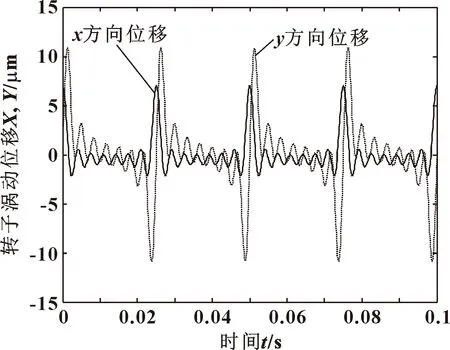
圖5 轉子渦動位移時域

圖6 轉子渦動位移頻域
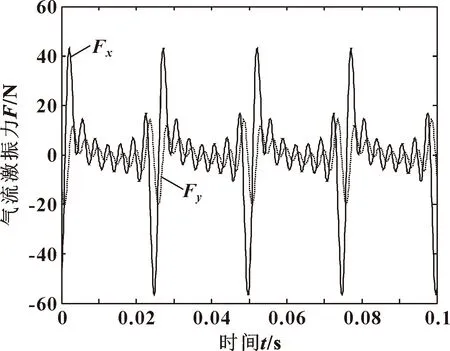
圖7 氣流激振力時域
由圖6所示的位移頻域圖可看出,在一些頻率處,渦動幅值與公式設定值有偏差,考慮是動網格變形和FFT計算誤差引起。因此,密封動特性系數求解中,不能采用公式計算獲得的渦動位移,而應采用CFD計算獲得的實際渦動位移。
由圖8所示的氣流激振力頻域圖可以看出,密封氣流力對應的頻率成分與施加在轉子上的渦動頻率相同,證明多頻法可準確捕捉對應渦動頻率下的氣流力。
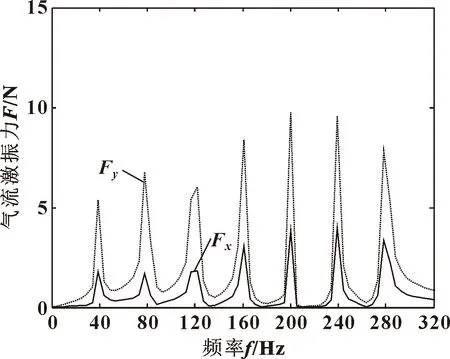
圖8 氣流激振力頻域
隨著轉子渦動頻率的增加,在同一渦動幅值下,x方向和y方向的氣流力均隨渦動頻率的增加而增大。
3.2 蜂窩密封動力特性分析
蜂窩密封和迷宮密封模型動力特性系數隨頻率的變化曲線如圖9所示。可以看出,轉子渦動頻率對蜂窩密封動力特性系數影響較大。在工況范圍內,隨著頻率的增加,蜂窩密封的直接剛度系數隨之增加,交叉剛度和直接阻尼均減小,交叉阻尼系數呈上升趨勢;有效阻尼系數隨渦動頻率增加而減小,有效剛度系數隨渦動頻率增加而增加。
如圖9所示,轉子渦動頻率對迷宮密封動力特性系數影響不是十分明顯,除迷宮密封主剛度隨渦動頻率增加呈現絕對值增大之外,其余參數變化較小。
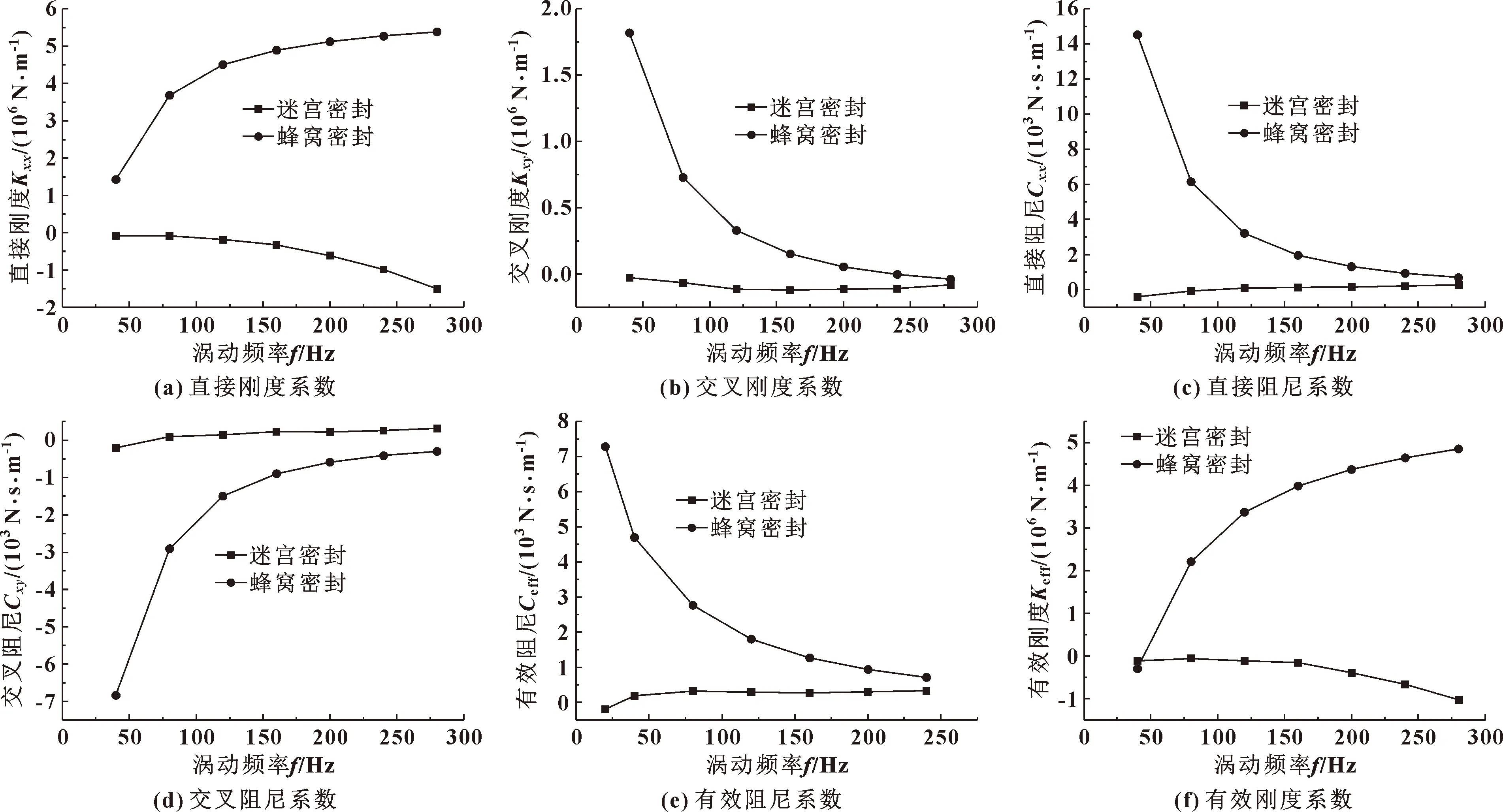
圖9 蜂窩密封與迷宮密封動力特性系數隨渦動頻率的變化
對比蜂窩密封和迷宮密封動特性參數結果可知,蜂窩密封的直接剛度系數、直接阻尼系數和交叉剛度系數均明顯大于迷宮密封;在低頻率區(f<80 Hz),蜂窩阻尼密封的有效阻尼系數是迷宮密封的10倍以上,可極大增加渦動阻力,增強轉子穩定性。
4 蜂窩密封轉子穩定性分析
針對某型高壓空氣離心壓縮機機組,進行蜂窩密封結構設計。轉子模型如圖10所示,圖中B1處為軸承,序號1-7為口圈密封,序號8為平衡盤密封。機組轉子總長1 800 mm,跨距1 200 mm,額定轉速10 500 r/min,進口壓力11 MPa,出口壓力20 MPa。機組平衡盤密封直徑200 mm,軸向長度90 mm。
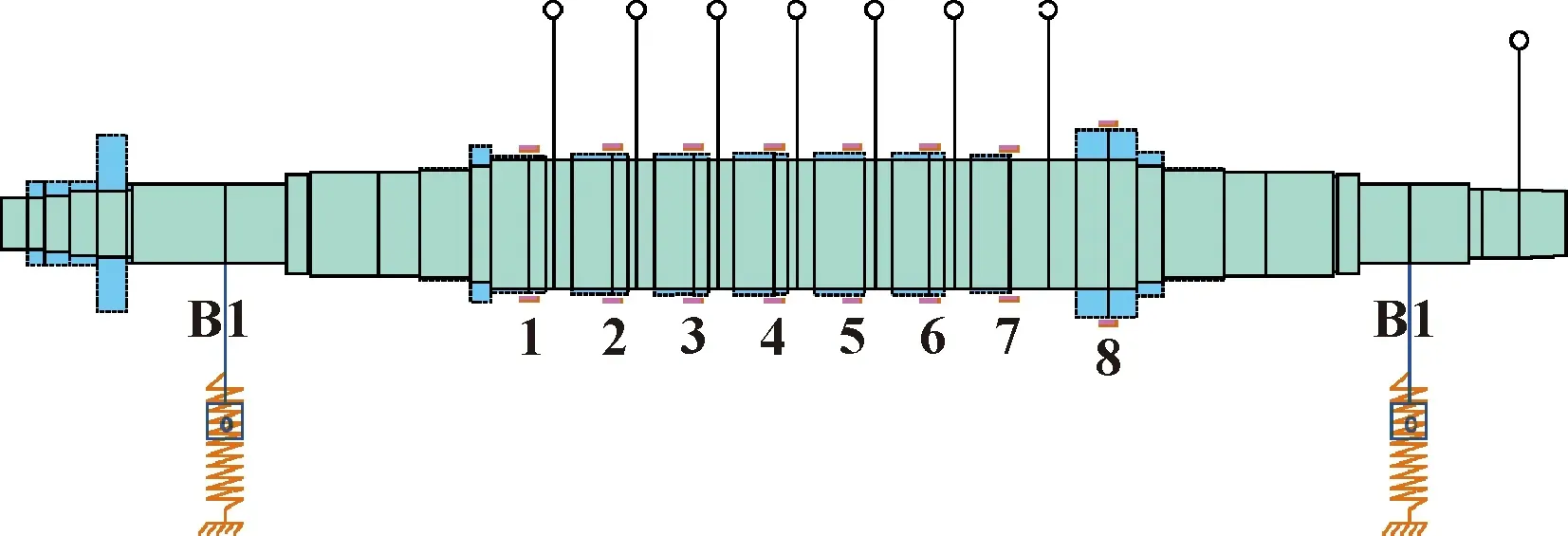
圖10 離心壓縮機組轉子模型
對平衡盤密封處進行蜂窩阻尼密封結構設計,采用前述CFD方法對蜂窩密封動特性參數進行計算,同參數下迷宮密封和蜂窩密封的動特性參數如表3所示。可看出,相比于迷宮密封結構,平衡盤應用蜂窩密封后,密封主阻尼大幅上升,雖然交叉剛度高于迷宮密封,但蜂窩密封的有效阻尼實現了大幅提升。

表3 密封動特性參數對比
對不同機組布置形式下的轉子系統進行動力穩定性分析,結果如表4所示。可以看出,在考慮密封動力特性參數后,轉子系統的動力穩定性都有降低,尤其是平衡盤密封采用常規迷宮密封設計時,轉子系統的對數衰減率為-0.02,遠低于行業通用標準的要求,而采用蜂窩密封的轉子動力系統穩定性明顯更優。

表4 轉子穩定性分析結果
采用常規迷宮密封設計時,實際機組在開車運行后,隨著壓力負荷提高,轉子系統表現出明顯的密封激振導致轉子失穩現象,無法達到額定設計工況點運行。將平衡盤密封由原來的迷宮型變為蜂窩密封后,通過機組現場的運行檢驗,機組各項運行指標完全達到設計要求,轉子系統動力穩定性得到明顯改善。
5 結論
(1)蜂窩密封動力特性系數隨轉子渦動頻率變化比較明顯,直接剛度系數和交叉阻尼系數隨渦動頻率增大而增大,交叉剛度和直接阻尼系數隨渦動頻率增大而減小。而迷宮密封動特性系數隨渦動頻率變化特征不明顯,僅主剛度絕對值隨頻率增加而增大,其余參數變化較小。
(2)不同渦動頻率下,蜂窩密封的直接剛度系數、直接阻尼系數和交叉剛度系數均明顯大于迷宮密封,交叉阻尼系數小于迷宮密封;此外,有效阻尼系數高于迷宮密封,特別在低頻率區,蜂窩阻尼密封的有效阻尼系數是迷宮密封的10倍以上。
(3)蜂窩密封在實際壓縮機轉子上的應用表明,相比傳統迷宮密封,蜂窩密封能夠顯著提升轉子對數衰減率,增加轉子動力穩定性,解決密封激振導致的機組振動問題。

