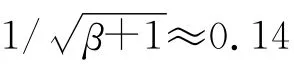漂浮于燒杯液體中的浮體微幅振蕩問題
張元元
(廣東省中山市中山紀念中學,廣東中山 528454)
2022年5月24日第6屆歐洲物理奧林匹克競賽(Eu PHO)剛剛落下帷幕,其理論第1題是一道有關浮體微幅振蕩問題.我們常見的浮體是指漂浮于廣闊的液體表面的物體,當浮體受到不是太大的擾動時,在液面附近振蕩的浮體的上表面始終位于液面之上,忽略浮體運動導致液體的運動,即忽略振蕩的液體對浮體運動的影響.本屆EuPHO 分析漂浮于燒杯液體中的浮體微幅運動,由于燒杯中液面有限,不能忽略振蕩的液體對浮體運動的影響,與此同時,還要進一步判定燒杯中哪部分液體的運動起到主導作用,從而構建模型計算振蕩運動的周期.
1 英文原題及中文翻譯
A solid,uniform cylinder of heighth=10cm and base areaS1=100cm2floats in a cylindrical beaker of heightH=20cm and inner bottom areaS=102cm2filled with a liquid.The ratio between the density of the cylinder and that of the liquid isγ=0.70.The bottom of the cylinder is above the bottom of the beaker by a few centimeters.The cylinder is oscillating vertically,so that its axis always coincides with that of the beaker.The amplitude of the liquid level oscillations isA=1mm.
Find the period of the motionT.Neglect the viscosity of the liquid.
一高度h=10 cm、橫截面積S1=100 cm2的固體均勻圓柱體漂浮在高度H=20 cm、內部橫截面積S=102 cm2的圓柱形燒杯里的液體中.圓柱體的密度與液體密度的比值γ=0.70.圓柱體的底部位于燒杯底部上方幾厘米處.當圓柱體在垂直方向振蕩,其軸線始終與燒杯軸線重合.已知液體振蕩的幅度A=1 mm.
試求振蕩運動的周期T.忽略液體的粘度.
2 分析系統振蕩情形以及構建系統振蕩模型
2.1 系統靜止時的相關參數
系統靜止時的立體圖以及側視圖如圖1 所示,浮力與重力相平衡,有

圖1 系統靜止示意圖

可知圓柱體浸沒液體的深度h0為

由于圓柱體的底部位于燒杯底部上方幾厘米處,燒杯的高度H=20 cm,我們可知圓柱體的頂部位于燒杯口部下方幾厘米處,液面更低于燒杯口.
2.2 系統微幅振蕩時的液面高度變化
當圓柱體在液面附近微幅振蕩時,燒杯中液面也在上下微幅振蕩.題中并未指明液體是否具有不可壓縮性,在缺乏條件下,我們顯然將液體視為不可壓縮流體,這樣我們進一步分析在實驗室參考系中,液面高度的變化量為y1.不失一般性,當圓柱體從平衡位置向下移動x時,如圖2所示,液體體積不變,有

圖2 系統振蕩示意圖

可知液面高度的變化量y1為

式中參量β=50.液體振蕩的幅度A=1mm 是指振蕩過程中y1的極大值是1 mm,因此圓柱體偏離平衡位置的最大值xmax=0.02mm,說明系統振蕩過程中液體的液面不僅低于圓柱體的頂部,更低于燒杯口,液體振蕩時不可能有液體溢出燒杯.
2.3 系統微幅振蕩時液體運動情形
系統振蕩時,圓柱體上下振蕩,液體的振蕩情形較為復雜,不僅圓柱體側面部分液體處于運動狀態,圓柱體底部以下部分液體也處于運動狀態.由(4)式可知液面向上運動的速度u與圓柱體向下運動的v之間的大小關系,即

圓柱體底部以上部分液體向下運動情形甚為復雜,其運動速度的上限值近似等于圓柱體運動的速度v.假設圓柱體底部以下液體的深度d=5cm,其動能上限值Ekb約為

由于液體具有不可壓縮性,圓柱體側面部分液體向上運動的速度均為u,其動能Ek為

Ekb與Ek的比值為

從結果可以看出Ekb?Ek,忽略圓柱體底部以下液體運動是合理的,建立振蕩模型時,僅考慮圓柱體側面部分液體的運動.
2.4 系統微幅振蕩時圓柱體受到的浮力作用
當圓柱體向下運動的加速度為a時,其側面部分液體向上運動的加速度a*為

此時圓柱體浸沒在液體中的深度y為
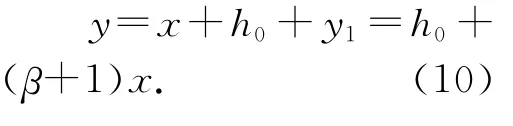
圓柱體受到的浮力寫成如圖3所示的形式是錯誤的,該浮力公式是針對液體加速度為0 的情形,對圓柱體側面液體受力分析,有

圖3 錯誤浮力示意圖

可知圓柱體底部壓強p與液面上方大氣壓強p0的差值為

圓柱體受到的浮力F為

3 分析微幅振蕩運動的周期
3.1 動力學特征方程法
由于圓柱體振蕩周期與系統振蕩周期是一致的,選擇圓柱體作為分析的對象,如圖4所示,振蕩過程中的動力學方程為

圖4 圓柱體受力示意圖

由(9)、(10)、(13)、(14)式可得

考慮到微幅振蕩,x?1,a?1,略去二階小量β(β+1)ax,(15)式簡化后符合簡諧運動的動力學特征方程,即

因此振蕩的周期T為
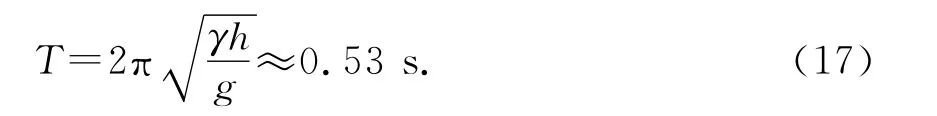
3.2 能量特征方程法
忽略液體的粘度,系統是一保守系統,當系統振蕩時,總的機械能E是恒定的.因此,我們也可以選擇系統作為分析的對象,振蕩過程中系統的動能Ek可表示為

忽略高階小量(β+1)x,動能Ek為

系統處于平衡位置時,系統的重力勢能記為E0.當圓柱體從平衡位置向下運動的距離為x時,液面的高度上升了y1,根據割補法可知液體重力勢能的增加量等于橫截面積為S1、深度為x的液體勢能增大到液體表面處橫截面積為S-S1、深度為y1時液體的勢能,該部分液體重心升高的高度hC為
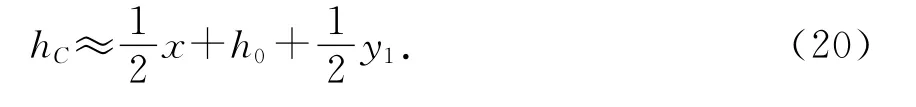
考慮到圓柱體重力勢能減小,此時系統的重力勢能Ep可表示為

最終系統的重力勢能Ep為

根據系統機械能守恒條件,即Ek+Ep=E,可知系統的能量方程為

(23)式關于變量x及其一階導數v的方程符合簡諧運動的能量特征方程,振蕩周期T為

4 總結