基于滾動時域的無人水稻直播機運動狀態估計

武 濤 李彥明 徐長賡 劉漢文 陳小倩 劉成良

(1.上海交通大學機械與動力工程學院， 上海 200240； 2.上海上實現代農業開發有限公司， 上海 202183)

0 引言

在水稻直播機實際的自主作業過程中，傳感器易受到環境狀況的干擾導致測量輸出不準確或者某些狀態難以測得。此外，由于水田環境結構復雜多變，也會給直播機帶來許多不確定性擾動[1-3]。因此，為提高水稻直播機在自動駕駛過程中的抗干擾能力以及得到較為準確合理的狀態值，需采取一定的狀態估計方法。

許多學者在自動駕駛車輛狀態估計方法上進行了大量的探索研究[4-11]。作為一種基于模型在隱馬爾可夫鏈上的遞歸貝葉斯估計，卡爾曼濾波(Kalman filter, KF)相關理論已非常成熟[12-13]，被證明是無約束系統最小方差意義下的最優估計，目前是無約束動態系統狀態估計應用最普遍的方法[14-17]。基于線性模型的KF針對非線性模型無法實現精確估計，而采取將非線性模型線性化的擴展卡爾曼濾波(Extended Kalman filter, EKF)和基于UT變換的無跡卡爾曼濾波(Unscented Kalman filter, UKF)能較精確地實現對無約束非線性模型狀態的估計[18-22]。文獻[18]提出一種基于EKF的多傳感融合通用框架，用于微型飛行器導航定位。該算法理論上能處理無限多類型傳感器及其延遲，以及傳感器相對或絕對測量，最終對飛行器的狀態信息進行估計。文獻[20]分別采用EKF和UKF估計航天器的位置和速度，結果表明UKF的平均估計精度較高，因為使用先驗測量分布的無跡變換(UKF)比基于線性近似的EKF更接近原始分布。文獻[22]使用UKF融合GPS、IMU和車輪編碼器的測量值對車輛姿態進行估計，使用Stanley控制器作為路徑跟蹤控制算法，提高了車輛自動駕駛的定位精度和魯棒性。雖然卡爾曼濾波被廣泛應用，但是它不能處理狀態量的約束，有可能出現不符合物理實際的估計值，并且它要求系統模型必須準確，否則可能出現發散的情況。

基于滾動優化原理的滾動時域估計(Moving horizon estimation, MHE)通過將狀態估計問題轉化為固定時域的優化問題，能較好地處理狀態量的約束和帶有不確定性的非線性系統，目前在跟蹤定位、故障診斷、參數估計等領域得到了廣泛的研究與應用[23-30]。文獻[25]使用MHE狀態估計方法解決傳感器具有時滯、丟失值和不同頻率的問題，此外，還引入了線性模型MHE的高效計算方法，但僅適用于可以找到線性MHE問題解析解的情況。文獻[27] 針對移動機器人的位姿估計問題提出一種基于MHE高效通用的多傳感器融合方案，此方案基于多線程架構，降低了計算成本。利用仿真和真實實驗數據對該方案進行測試，并與UKF進行比較，結果表明MHE估計性能優于UKF。文獻[30]基于縱滑側偏聯合工況下的八自由度整車模型，并考慮車輛系統現實存在的物理約束，使用MHE對車輛的速度等參數進行了估計，估計結果較為符合實際情況。

針對無人水稻直播機自動駕駛過程中難以獲得精確的車輛模型以及傳感器測量存在誤差等問題，本文設計一種基于滾動時域的車輛運動狀態估計方法，在每個采樣區間內通過求解優化問題的極小值估計出車輛在當前時刻的狀態值：橫向偏差和航向角偏差，以提高車輛的抗干擾能力和路徑跟蹤控制精度。

1 滾動時域估計原理

基于模型預測滾動優化原理來討論MHE的數學原理，受擾動離散的非線性狀態空間表達式為

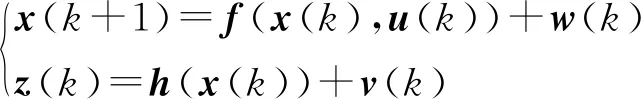
(1)

式中k——采樣時刻x(k)——狀態變量

u(k)——控制輸入w(k)——外部干擾

z(k)——測量向量v(k)——測量噪聲

f、h——非線性過程和測量模型

狀態值和測量值歷史序列為

(2)

(3)

式中Qi、Ri——正定的懲罰矩陣，反映對模型干擾和測量噪聲的程度，通常為方差的對角矩陣

通過最小化式(3)可以求出歷史所有狀態的估計值，只取最后一個估計值作為當前時刻的狀態值。新的采樣時刻到來，將新的測量數據補充進測量序列，在線重新求解式(3)。但隨著時間的增加，數據越來越多，優化問題越來越復雜，直至不可解。并且隨著時間的推移，過久的數據對當前狀態的影響逐漸降低，因此，引入固定時域窗口N，考慮固定窗口的滾動時域估計，只使用最近N個狀態值和測量值，有

(4)

將系統模型作為等式約束，加上狀態和控制的不等式約束，用優化問題替代全信息MHE問題,有

(5)

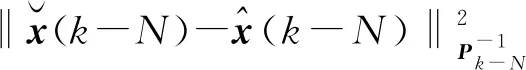
(6)

其中

(7)

式中Fk、Hk——系統模型和測量模型雅可比矩陣

由此，通過MHE算法將狀態估計問題轉換成固定時域的優化問題，處理了系統約束、模型干擾和非線性以及測量噪聲，能提高估計的合理性和準確性。

2 基于MHE的直播機運動狀態估計器

2.1 帶擾動的直播機運動學模型

要控制車輛首先要對車輛的運動建立數學模型，模型越精確對車輛的運動描述就越精確。由于在高度非結構化水田環境下，直播機動力學模型參數難以獲取，因此建立簡單易用的運動學模型。不考慮車輛在垂直方向的運動，假設車身系統為剛性，左右側車輪具有相同的轉向角度和速度，忽略車輛動力學特性，將直播機簡化為二輪車模型，如圖1所示。圖中，M(xm,ym)為車體控制點；A(xa,ya)、B(xb,yb)為期望路徑P上的兩點;θp為航向角的期望值。用橫向偏差、航向角偏差、前輪轉角、行駛速度和前后輪軸距等參數建立直播機的運動學模型，從而描述直播機的運動狀態。

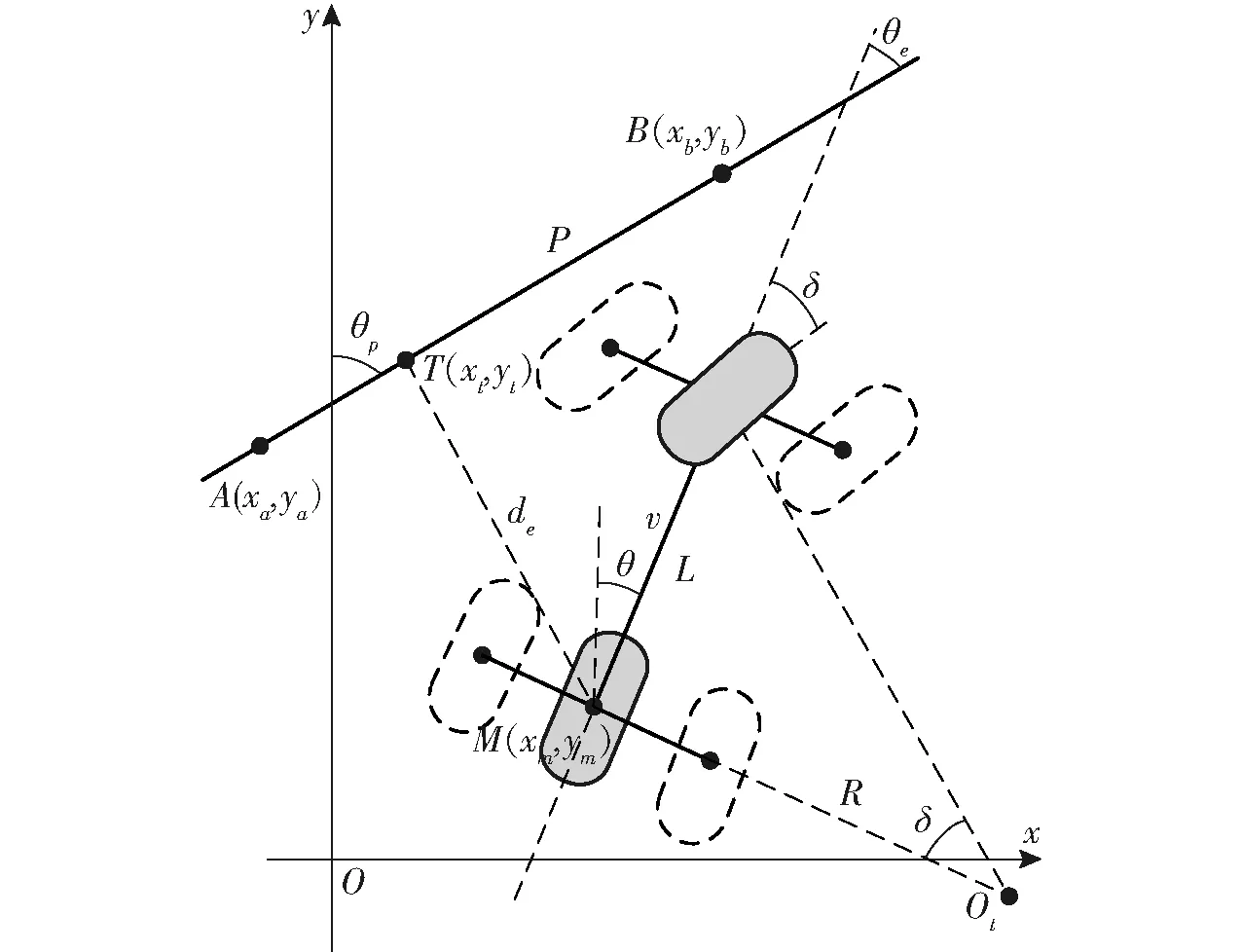
圖1 水稻直播機運動學模型Fig.1 Kinematic model of rice seeding machine

由于期望路徑AB固定，所以航向角偏差的導數與航向角速度相等，即

(8)

式中v——速度，m/s

R——轉彎半徑，m

θ——航向角，(°)

θe——航向角偏差，(°)

由圖1中幾何關系可得

(9)

式中L——前后輪軸距，m

δ——前輪轉角，控制輸入，(°)

因此

(10)

橫向偏差的導數即為速度v在該方向上的分量，即

(11)

式中de——橫向偏差，m

以橫向偏差de和航向角偏差θe為狀態變量，同時考慮水田中地況復雜多變具有許多不確定性干擾，為避免未知干擾導致建模不準確，引入復合干擾項：橫向位置干擾|w1|≤P和航向角干擾|w2|≤K，P和K為干擾的最大值，由式(10)、(11)可得帶干擾的直播機運動學模型為

(12)

在實際應用中使用的是車輛離散模型，因此需對連續模型進行離散化。令采樣周期為T，對式(12)進行前向歐拉離散化得

(13)

式(13)離散模型的狀態量是基于橫向偏差和航向角偏差，可由車輛裝載的RTK-GPS傳感器測出的位姿信息與期望位姿信息計算，由此得測量模型

(14)

式中v1、v2——測量噪聲

2.2 MHE估計器方案

式(13)、(14)為直播機離散的非線性狀態空間表達式，可代入式(1)，通過MHE的求解公式(5)進行直播機運動狀態：橫向偏差和航向角偏差的估計。可得MHE算法流程：

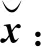
(3)根據式(6)、(7)計算時刻k處狀態的后驗估計協方差矩陣Pk。

(4)在k+1時刻，得到新狀態的測量值，更新窗口N內的數據，重復步驟(2)、(3)。

優化問題(式(5))的計算成本高度依賴于窗口N的大小，如果計算時間超過了傳感器的最大采樣周期，估計出的狀態則不是當前采樣時刻的，需采取一定的方法提高MHE的計算效率。如圖2所示，提出一種基于多線程的系統架構，為M個主要傳感器的數據接收、分析與處理開辟單獨的線程，用來構建測量矩陣，最后傳遞給MHE求解線程進行優化問題的求解。多個線程并行工作，可減少MHE總體計算時間，提高MHE采樣頻率。

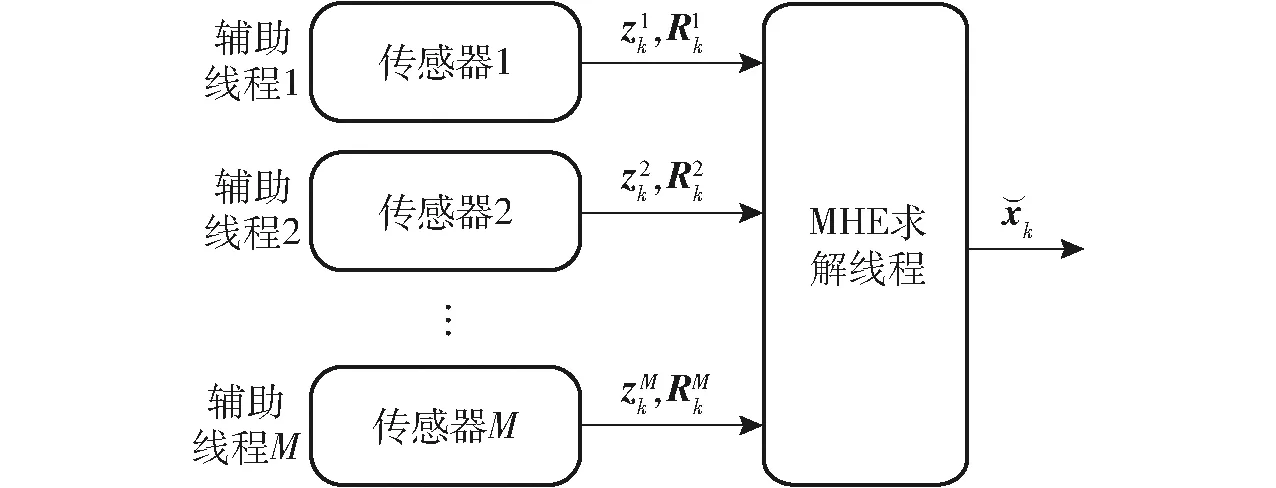
圖2 多線程MHE求解架構Fig.2 Multi-threading architecture of MHE

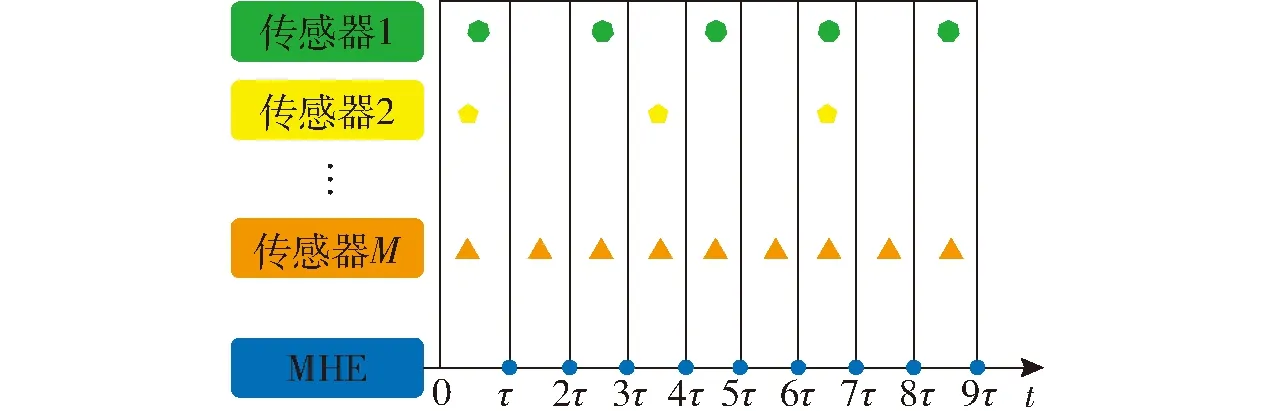
圖3 多頻率傳感器解決方案Fig.3 Solution of multi-frequency sensors

如圖3所示(圖中τ為所有測量傳感器采樣周期最大值)，該多線程架構也能解決多個傳感器具有不同的測量頻率。圖中不同多邊形代表每個傳感器產生的有效值，雖然不同傳感器的數據可能會在不同時刻收到，但每個傳感器線程都會在有新數據到達時更新數據，因此傳給MHE求解線程的數據都是最新窗口內的。針對傳感器出現的異常值使用馬氏距離閾值法進行檢驗剔除，計算式為

(15)

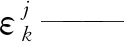
ζj——馬氏距離閾值

3 仿真驗證

使用Matlab仿真驗證MHE狀態估計算法的有效性。根據圖4控制系統結構圖建立相應的仿真模型。控制算法采用文獻[3]提出的快速終端滑模控制器，控制車輛從起點移動到終點，通過向直播機運動學模型和狀態值加高斯白噪聲來模擬系統干擾和測量誤差。使用MHE和EKF對帶噪聲的狀態進行估計并與系統狀態真值比較，觀察MHE和EKF的估計效果。直播機系統控制仿真參數同文獻[3]，MHE仿真參數選取如表1所示。

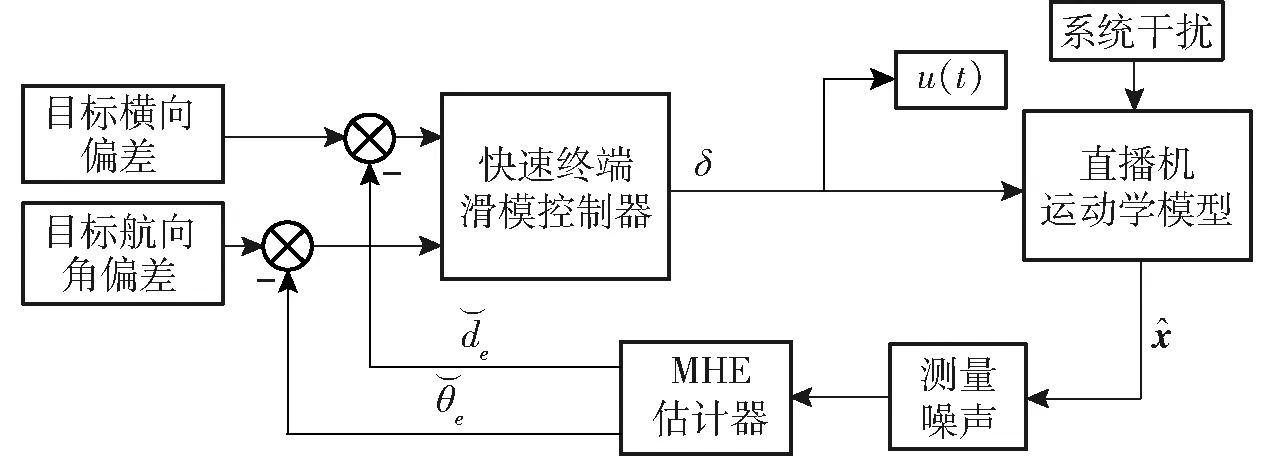
圖4 控制系統結構圖Fig.4 Block diagram of control system

考慮MHE計算時間不能超過傳感器采樣周期0.05 s，經過仿真測試選取時域窗口值N等于5，單次計算所需時間約為0.01 s，滿足在線實時估計要求。使用高效的優化控制軟件CasADi表述優化問題，然后使用內點法求解該優化問題。圖5、6是整個行駛過程中車輛橫縱坐標和航向角變化，藍色曲線是仿真得到的系統真值，紅色曲線是帶噪聲的測量值，綠色曲線在圖5、6中分別是使用MHE和EKF估計出的狀態值。可以看出，測量值具有很大的不確定性，在真值附近波動，使用MHE和EKF能有效地從測量值中估計出較為準確的狀態值。

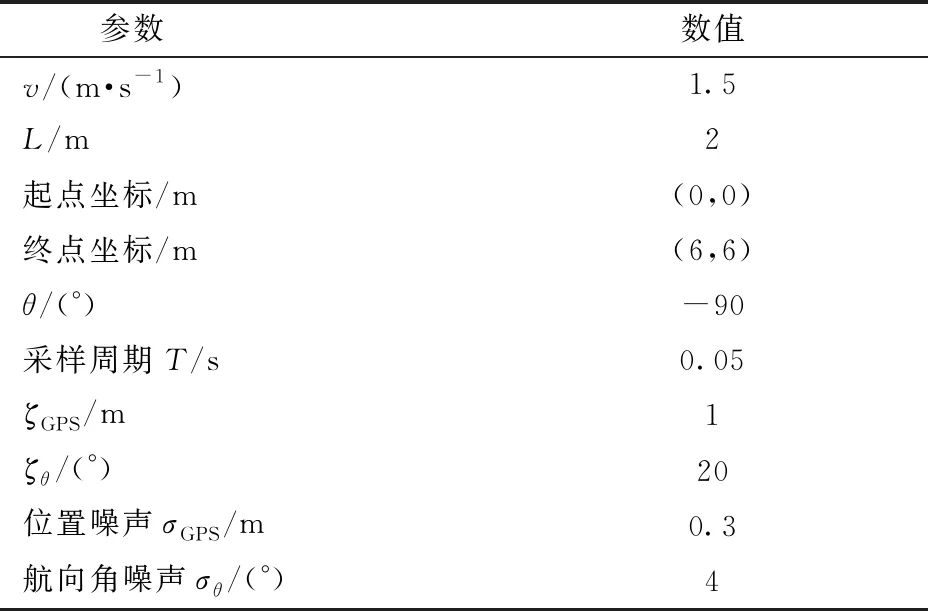
表1 MHE仿真參數Tab.1 Simulation parameters of MHE

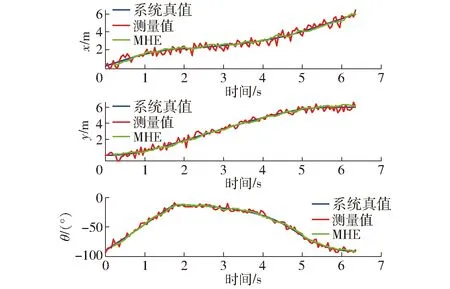
圖5 MHE狀態估計結果Fig.5 States estimation results with MHE

圖6 EKF狀態估計結果Fig.6 States estimation results with EKF

圖7為MHE和EKF狀態估計絕對誤差散點圖，平均絕對誤差如表2所示。可以看出，MHE和EKF狀態估計誤差總體上比測量值誤差小很多，說明二者具備從不確定信息中提取精確信息的能力。此外，MHE狀態估計誤差也比EKF狀態估計誤差小，說明基于優化方法求解的滾動時域狀態估計優于傳統的基于估計誤差協方差的狀態估計，證明了本文所提MHE狀態估計算法的有效性。

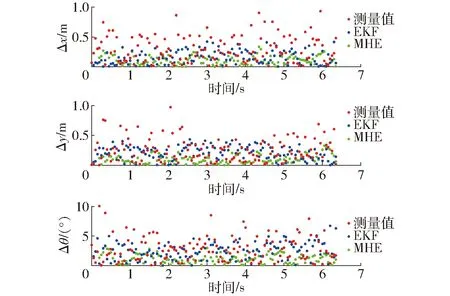
圖7 MHE與EKF狀態估計絕對誤差Fig.7 Estimation error of MHE and EKF

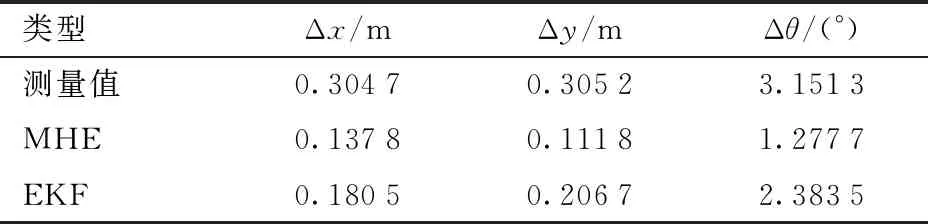
表2 狀態估計平均絕對誤差Tab.2 Mean absolute error of states estimation

4 試驗驗證

4.1 試驗平臺

試驗采用中國洋馬農機有限公司生產的YR10D型水稻直播機，對該型號直播機進行自動駕駛改造，如圖8所示。自動駕駛系統主控制器采用裝載Linux系統的工業計算機，具有4核1.6 GHz高性能處理器、1 GB DDR3運行內存、4路帶隔離的3線 RS-232串口，1路CAN總線以及1路100 M以太網等通信接口。上位機主控制器通過CAN/RS-232的通信方式與車身各子系統進行數據交互與協作，完成直播機自動駕駛和自主作業。下位機控制器為自行設計的STM32嵌入式控制器，具備CAN/RS-232通信方式。采用北京天海科公司生產的DWQT-CAN-360-G型轉角傳感器，精度為0.1°，通信方式為CAN總線。RTK-GPS使用4G網絡差分基站，動態定位精度在±0.02 m，數據刷新率為20 Hz，通信方式為RS-232。方向盤使用直流電機驅動，采用位置-速度雙閉環控制，通信方式為RS-232。

圖8 無人駕駛水稻直播機Fig.8 Unmanned rice seeding machine

該無人水稻直播機具備自動駕駛作業、精量播種、種箱容量檢測及堵塞報警、自動倒車和全地塊封邊作業等功能。同時在阿里云服務器上搭建云監控管理系統，能實現遠程監控、路徑規劃及多機協同作業管理。貫徹了“智慧在云，智能在端，管控在屏”的未來無人農場設計理念。

4.2 水稻直播機水田無人作業試驗

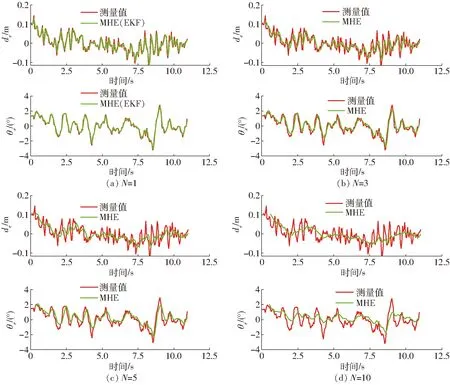
圖10 橫向偏差與航向角偏差估計結果Fig.10 Estimation results of lateral deviation and heading angle deviation

為驗證本文所提MHE估計算法對無人水稻直播機運動狀態的估計效果，在上海市崇明區上實現代農業開發有限公司建立的無人農場里使用圖8所示直播機進行實際無人播種作業。圖9為直播機一次試驗時部分作業軌跡，可以看出，雖然直播機行駛軌跡總體較為平穩，但由于水田中具有許多不確定性干擾以及傳感器測量帶有噪聲，直播機行駛軌跡在某些區域也會出現一定抖動。為了獲取更加準確的狀態值從而抑制這些抖動，獲取8段直線行駛路徑的直播機運動狀態de和θe，使用MHE算法進行估計。

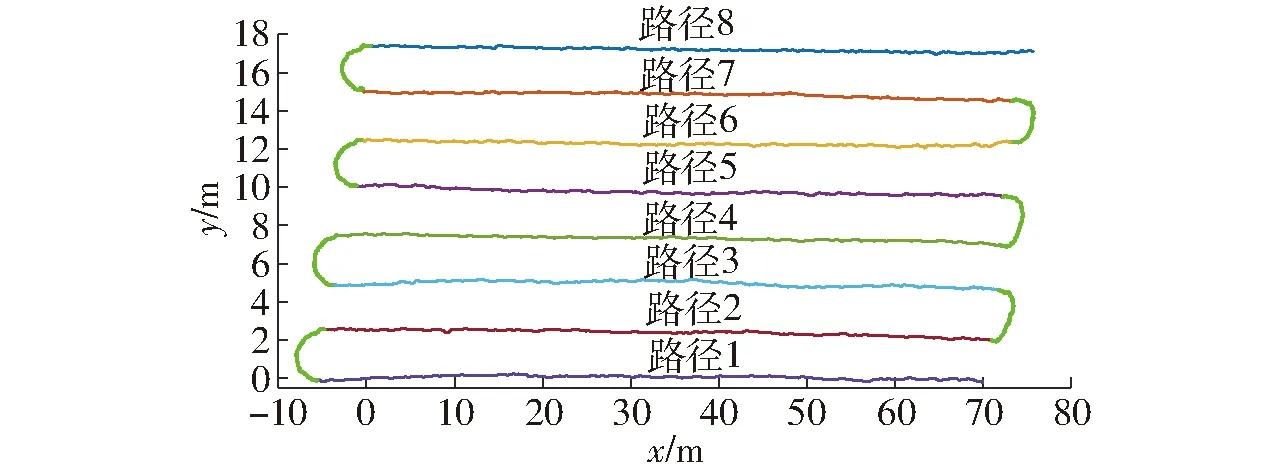
圖9 直播機作業軌跡Fig.9 Driving paths of rice seeding machine

選取路徑4分析時域窗口N的大小對MHE估計效果的影響。圖10為N等于1、3、5、10時，使用MHE對橫向偏差與航向角偏差的估計結果。可以看出，由于水田中具有許多不確定性干擾以及傳感器測量帶有噪聲，測量值在短時間內存在較大跳變，控制器算出的控制量也會不穩定，從而導致車輛發生抖振。可以看出，MHE估計后的狀態變化相比測量值更加平穩，具有一定抑制干擾的能力。根據MHE的原理可知，N等于1時MHE算法是一種EKF算法，此時估計值與測量值基本吻合，只在波峰波谷處對測量值的不穩定具有一定的抑制作用。N越大對系統干擾和測量誤差的抑制能力越強，但過大不能反映正常的狀態變化，因為隨著時間的推移，越早的數據對當前時刻的參考意義越小。如N等于10時，MHE估計值偏離測量值過多，不符合實際情況。因此，為保證MHE對系統干擾和測量誤差的抑制具有良好的效果，同時也能較好地反映狀態的真實變化，一般N取3～5，此時整體估計效果也優于EKF算法(N=1)。

圖11為N=3時，使用MHE算法對直播機 8段路徑橫向偏差與航向角偏差的估計結果。可以看出，8段路徑中橫向偏差基本保持在-0.1～0.1 m，航向角偏差基本保持在-2°～2°，但橫向偏差測量值出現全程不平穩現象。MHE估計算法能有效改善這種現象，使得狀態值變化平穩同時也能反映出實際變化趨勢。說明MHE能有效消除系統干擾和測量誤差對橫向偏差的影響。相對來說航向角偏差變化較平穩，沒有較多噪聲，MHE估計算法對減小其變化幅值起到一定作用。對試驗數據分析發現，每段路徑相對于理想軌跡都會有一定的橫向位置和航向角穩態偏差。如表3，各段路徑穩態偏差基本一致，其中橫向穩態偏差均值為-0.068 8 m，航向角穩態偏差均值為-1.467 0°。使用MHE估計后各穩態偏差大幅下降，橫向穩態偏差與航向角穩態偏差均值分別為-0.019 4 m和-0.366 5°，說明MHE估計算法能消除干擾給狀態帶來的穩態偏差。

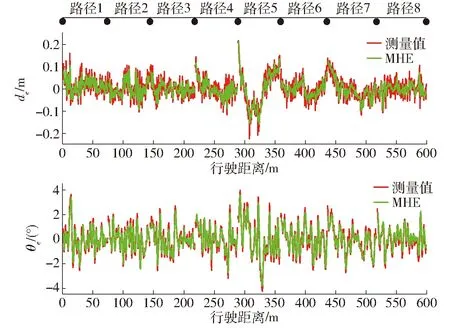
圖11 所有路徑橫向偏差與航向角偏差估計結果Fig.11 Estimation results of lateral deviation and heading angle deviation of all driving path

各段路徑估計結果顯示，本文提出的基于滾動時域的水稻直播機運動狀態估計算法能從不確定的狀態信息中得到較為準確的狀態值，能較好地消除系統干擾和測量誤差 ，對下一環節的精確控制具有實際意義。

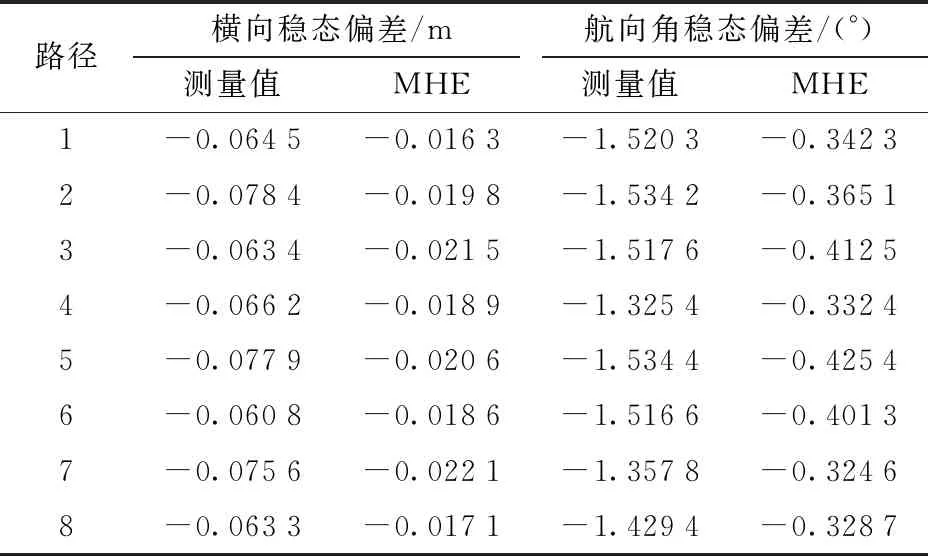
表3 各段路徑橫向與航向角穩態偏差Tab.3 Steady-state error of lateral and heading angle

5 結論

(1)基于帶系統擾動的非線性水稻直播機運動學模型和帶噪聲的測量模型，提出一種基于滾動時域的無人水稻直播機運動狀態估計算法。同時，為提高MHE狀態估計算法的計算效率和解決傳感器采樣頻率不同的問題，提出一種基于多線程的MHE求解架構。使用Matlab/CasADi進行系統仿真，結果表明，本文提出的MHE狀態估計算法能有效補償系統干擾和消除測量噪聲，得到接近理論真值的狀態，而且MHE的估計效果優于EKF。

(2)在上海市崇明區無人農場進行了水稻直播機無人作業試驗，使用MHE算法對某段直線路徑中測得的橫向偏差和航向角偏差值進行估計。試驗結果顯示，時域窗口N取3～5時，MHE對補償系統干擾和消除測量誤差具有良好的效果，同時也能較好地反映狀態值的真實變化。

(3)使用MHE狀態估計算法對水稻直播機8段路徑的橫向偏差與航向角偏差進行估計。結果顯示，MHE算法對消除橫向位置、航向角的穩態誤差和抑制測量值的不平穩性具有良好的效果，同時也能反映出實際狀態變化趨勢，證明了MHE狀態估計算法在補償系統干擾和消除測量誤差方面的優異性。